基于OpenMP的多核并行技術在電力系統工頻電場計算中的應用

劉 哲，李永明，周 悅，鄒岸新，徐祿文

（1. 重慶大學電氣工程學院，重慶 400030；2. 國網重慶市電力公司電力科學研究院，重慶 401123）

0 引言

我國地緣遼闊，特高壓輸電能夠實現大容量、遠距離輸電，降低損耗，節省線路走廊，有利于構建堅強電網[1]，正是高電壓等級輸電的這些優勢，我國近些年發展建設了很多特高壓線路。隨著高壓輸電線路電壓等級由超高壓升高為特高壓，特高壓輸電系統電壓高、電流大，帶電導體表面及附近空間的電場強度明顯增大，電暈放電產生的可聽噪聲和無線電干擾影響突出[2]。輸變電系統電磁場的工程計算是一項需要追求精度和時間的任務，為得到更為準確的結果，輸電線路的仿真計算趨于三維化，同時考慮的環境因素也趨于復雜化，這些所帶來的直接結果是所要計算的數據越來越多，給計算機帶來了前所未有的挑戰，所以怎樣快速并又準確的計算出周圍的電磁場分布一直是科研工作者追求的目標。

計算機技術日新月異，將計算機的技術優勢最大限度地應用于電力系統，是目前國際智能電網的研究重點之一[3]。其中，計算機技術中的并行計算是解決大數據計算與時間復雜度之間矛盾的有效方法，也只有并行計算機可以解決今天日益增加的計算需要所面臨的困難[4]。并行計算也不是什么新鮮事，在光化學，以及當下熱門的云計算領域都有并行計算的身影[5]-[11]。并行計算就是可以同時對多個任務，多條指令進行處理，從而縮短計算時間提高計算的效率。目前并行計算主要有 2種方式，MPI和 OpenMP。MPI是通過多機群組合，并在機間通過消息傳遞的方式進行交流，達到并行計算的效果。但這種多機集群環境，內存不共享，在全局共享數據讀寫操作中，必須依靠機器間的通信來進行數據搬遷[12]，所以往往造成通信開銷遠遠高于計算本身所花的時間。而多核環境中內存是共享的，可以省下通信開銷，鎖操作的效率遠大于通信效率，并且在過去計算機的發展中，計算機都是單核高頻的追求計算性能，但是在現有工藝下，改善 CPU 性能的傳統方法如提升時鐘速度和指令吞吐量等在摩爾定律限制下已經難有大的進展，單核發展已處于瓶頸狀態，多核計算將成為未來的發展趨勢[13]，所以過去的多臺單核計算可以簡化到現在一臺多核計算機上，實現經濟優化，編程優化等優勢。

因此，本文采用可應用于單機多核的 OpenMP的并行計算方法，結合模擬電荷法研究特高壓輸電走廊的電場并行計算，仿真分析了離地1.5m工頻電場的分布，對比串行算法驗證其準確性，并分析并行計算在效率上的優勢。

1 OpenMP 并行計算

OpenMP是一個為共享存儲結構計算編寫并行程序的接口，1997年10月，由SGI公司發起，HP、SUN、IBM和Intel等聯合開發和推行一種新的共享主存編程模型的建議標準。其跨平臺，可伸縮的模型給并行程序的設計者在桌面電腦和巨型機上開發并行程序提供了簡單靈活的接口，在不降低性能的情況下克服了機器專用編譯指示所帶來的移植性問題，得到了各界的認可和接受[14]。編程模型以線程為基礎[15]，主要應用于對稱式共享存儲器多處理機結構的并行計算機（SMP）。SMP是一類常見的共享存儲并行計算機，其內部結構圖如下1所示。

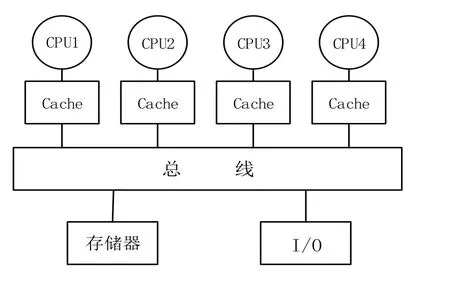
圖1 SMP 結構圖Fig.1 Structure chart of SMP

該類結構最重要的兩個特點就是對稱性和共享性，對稱性是指系統中各個處理器的結構相同，地位相等，可以對稱地訪問存儲器以及 I/O設備；共享性指的是存儲器的地址共享，具有統一且唯一的地址空間，所有的處理器共享該地址空間。

OpenMP最基本的執行模式為fork/join并行執行模型，它編程簡單并且可以增量開發。在OpenMP編程中，整個程序被看作一個大的串行執行結構，也可以叫做隱式初始任務區，并行結構只是其中的一個執行單元。并行結構中可以嵌套多個子并行結構，如果環境變量設置允許嵌套并行，這些嵌套子并行結構內還包含多個子孫并行結構。如圖2所示，執行過程大致為，一個OpenMP程序從一個主線程開始，在程序某點需要并行時程序派生出一些額外的線程組成線程組，被派生出來的線程稱為組的從屬線程，并行區域中的代碼在不同的線程中并行執行，當并行域中的代碼執行完之后，其他并行線程銷毀，控制流程回到單獨的主線程來執行[16]。由于是共享內存的編程模型，降低了通信開銷，用戶不必處理迭代劃分、數據共享、線程調度及同步等低級別的細節[17]。

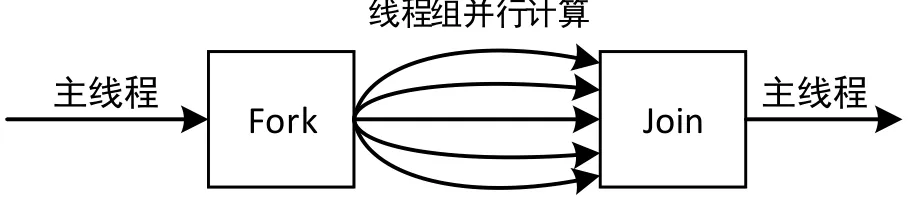
圖2 并行流程Fig.2 Parallel process

該模式的關鍵是判斷數據間的依賴性，如果不存在依賴性，則可以直接插入#pragma omp parallel for 編譯；如果存在依賴性，則需要對數據進行分析，查看是否可以通過循環變換或者分塊等技術手段消除依賴性，或者進一步發現其內在的并行性。

2 模擬電荷法基本原理

CSM是基于電磁場的唯一性定理和等效原理，其原理簡明，在具備場的基本概念的基礎上，方法應用較為簡捷，并可獲得足夠的計算精度[18]。其基本原理就是通過一組離散化的模擬電荷替代介質邊界面上連續分布的束縛電荷，在已知電位的原邊界面上設定與模擬電荷數目相當的匹配計算點，應用疊加原理建立各匹配點的電位方程，求解出各模擬點電荷值，并應用疊加原理得到場域中其他任意點的電位和電場值。

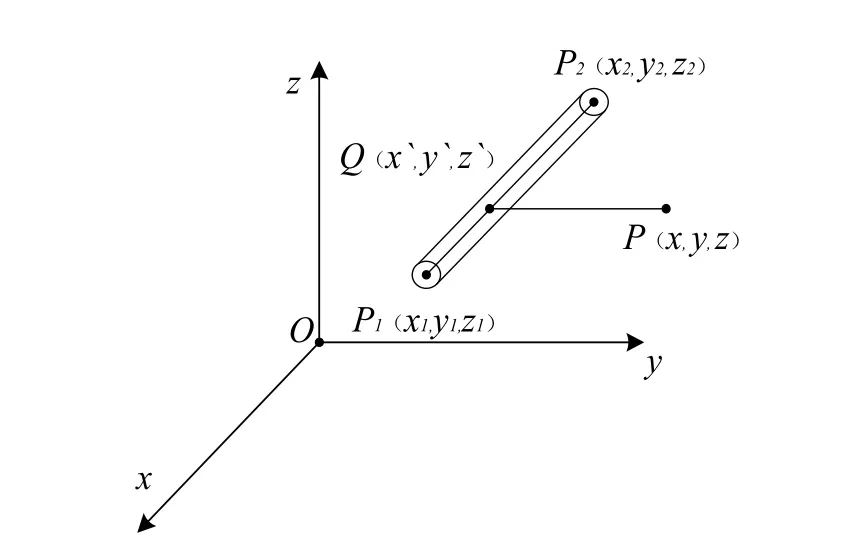
圖3 單元線電荷Fig.3 Unit of line charge

圖3 為單元線電荷計算示意圖。將導線分為若干個有限長線段，每一線段用線性模擬電荷等效，設空間中有一直線段。

計算時，首先分段并對大地做鏡像處理，求出各個匹配點產生的電位系數 P，再根據已知的邊界條件建立如下矩陣方程：

pτφ= （1）

式中，p為輸電線電位系數矩陣，τ為待求的線電荷列向量；φ為輸電線匹配點電位列向量。

通過求解該方程，解出電荷的值，再根據電荷與電場之間的關系，計算出三個方向上的電場值Ex、Ey、Ez，然后再合成，求得空間中任意點P(x,y,z)產生的電場強度為：

3 并行計算

由于OpenMP比較方便的植入性，使原有的串行程序并行化，因此編程的時候首先編寫輸電線下建筑物周圍電場計算的串行程序，然后再充分挖掘程序中可并行部分，對其進行并行程序編寫，實現并行計算、提升計算的效率。

文中程序在裝有 4核主頻 3.30 GHz 的 Xeon CPU的服務器（內存8 G），Windows 10 64位系統上采用 C和 Matlab混合編寫，C語言編譯器Microsoft Visual Studio 2010版，在充分利用Matlab對于矩陣編寫和計算的便利性的基礎上，用VS2010編寫 C語言并加入 OpenMP增加并行性，再用Matlab調用C語言所得數據畫出仿真圖形。

具體的，在Matlab中根據模型的坐標建立相應的矩陣，再通過mexFunction函數調用Matlab中矩陣的首地址把數據傳入到C語言中，在C語言中進行并行程序的編寫，在 Matlab用 mex語句調用 C語言中所得的結果繪出仿真圖形。mexFunction函數的標準結構如下：

void mexFunction(int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[])

{；//相應的語句}

其中整型參數nlhs[]和nrhs[]分別為輸出參數個數和輸入參數個數，mxArray類型參數plhs[]和prhs[]分別為輸入參數的指針和輸出參數的指針。

4 計算實例及仿真結果

4.1 計算模型

計算模型選取500 kV超高壓輸電走廊，每相采用4分裂導線，導線間距為0.323 m，子導線半徑為0.0148 m；最低點離地14.19 m，檔距為400 m，相間距為11.8 m。兩個桿塔之間輸電線的懸掛形狀呈懸鏈線形狀，當輸電線兩端的懸掛點對地高度一致時，由于對稱性，弧垂的最大值則會出現在檔距的中間點處。懸鏈線方程如下：

式中，σ0為導線水平應力，MPa；γ為導線比載，N/m·mm2；l檔距，m；h導線最低點對地高度，m。

由于實際的超高壓輸電線路比較復雜，而有些因素的影響可以忽略不計，所以本文做如下簡化：1、輸電線表面等電位；2、地面是無窮大的導體，電位為零，沿線地面電阻率相同；3、認為電荷分布沿線路分布沒有畸變，不考慮線路上電位的變化；4、只考慮線路主要部分形成的電場，忽略桿塔、金具、絕緣子等附近物體的影響。

簡化后的模型如圖 5所示，以輸電線走向為 y軸，垂直輸電線方向為x軸，垂直向上為z軸，坐標原點取在輸電線中心位置。

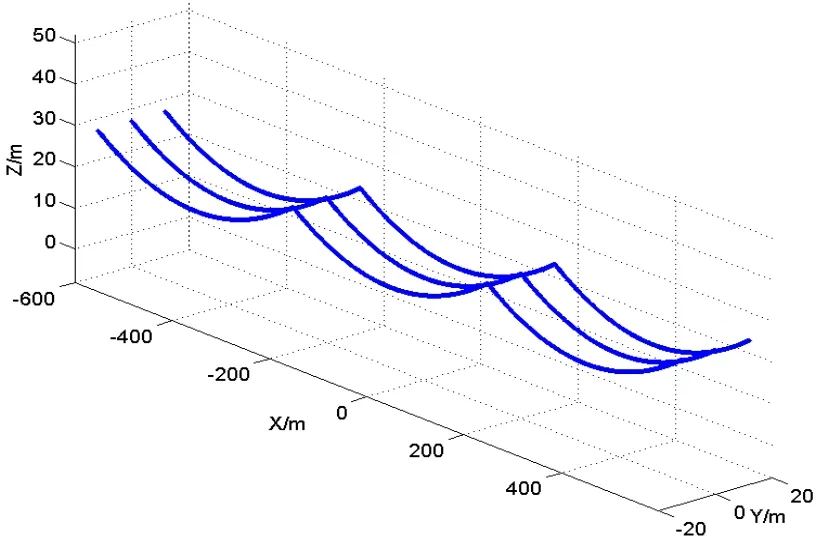
圖5 輸電走廊Fig.5 Pow er transmission corridor

4.2 計算精度

在精度方面，通過分別用Matlab和C語言并行編程計算，從量化的角度所得每一個點的電場結果作差比較，兩值的差值最大也只能達到小數點后 6位；從可視化的角度，圖6是取垂直于輸電線路并通過建筑物的中心平面，通過疊加作圖可以看到兩個數值作出來的曲線幾乎一模一樣，兩種角度證明了C語言并行計算下精度的可行性，并不會影響計算結果。

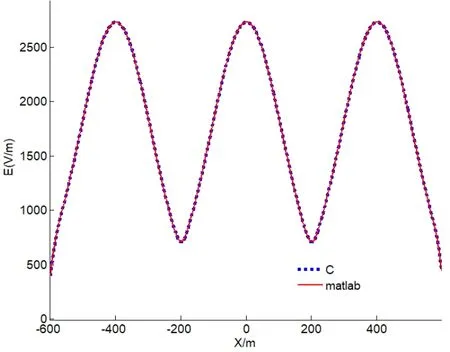
圖6 C 語言和Matlab的結果對比Fig.6 Comparative results of C and Matlab

4.3 計算效率

仿真分析了輸電走廊(x,y)=(-600~600，-20~20)，離地1.5 m工頻電場的分布首先本次的模型在Matlab下計算時間為 36342 s，而 C語言單核串行下計算時間僅為186.79 s，僅從串行計算的角度，C語言就是Matlab計算速度的194倍。

并行計算中，加速比S(p)以及并行效率E(p)是評價并行效果的重要指標，其中S(p)是P個處理器同時計算求解時，單核串行時間與多核并行時間之間的比值，即

式中，Ts是單個處理器在串行模式下計算所花費的時間；TP是P個處理器在并行模式下計算所花費的時間。

并行效率E(p)是加速比與計算時所用到的CPU核數的比值，如式（5）所示。當加速比與核心數P接近時，并行效率越高。

描述這兩個指標的重要定律：Amdahl定律。假設計算的問題固定規模不變，串行部分所占整個程序的比例f也不變，我們可以得到加速比S(p)為：

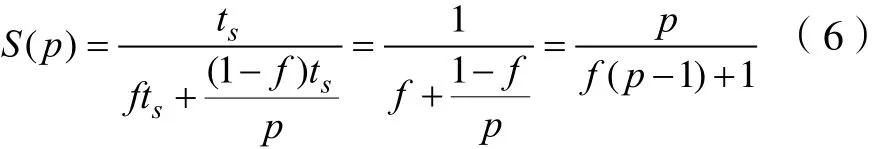
驗證并行計算的有效性，并且為了避免計算的波動性，對每種情況都進行10次計算。

效果圖如下所示：

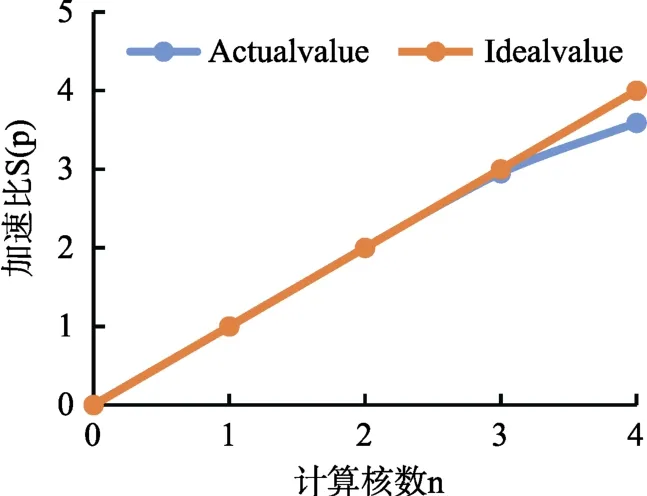
圖7 加速比Fig.7 Accelerate rate

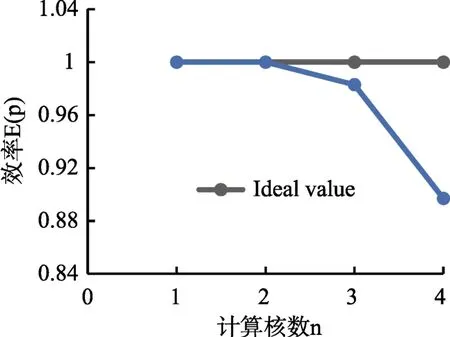
圖8 加速效率Fig.8 Accelerate efficiency

雙核模式下，加速比基本穩定在2.0，說明雙核情況下并行起到了很好的加速效果；同樣的模型在4核模式下，加速比為3.5以上，相比于4核情況下的理想結果有一點差距，原因之一是點電荷與線電荷計算的差異性，線電荷要進行較為復雜的積分運算，所以所花的時間相比點電荷較長，造成線程之間的等待；其次根據 Amdahl可知，串行占比也會對并行的效率造成影響。

5 結論

本文有別與傳統的只采用Matlab進行編程的模式，引入C語言與Matlab混合編程，并在模擬電荷法的基礎上引入OpenMP進行并行編程，既利用了Matlab生成矩陣的便捷性和對數據圖像處理的強大功能，又利用了C語言的對于計算的快速編譯性以及對于并行計算的可塑性，計算了500kV高壓輸電走廊下空間電場分布的情況，實現了對輸電線走廊周圍電場環境的快速求解，為其他類似電磁場數值計算提供了思路。

[1] 王艷, 王樹歡, 等. 特高壓六相輸電線路工頻電場強度計算[J]. 中國電力, 2015, 48(3): 44-49.WANG Y, WANG S H, et al. Calculation of Power Frequency Electric Field Intensity of UHV Six-phase Transmission Lines[J]. ELECTRIC POWER, 2015, 48(3): 44-49.

[2] 劉振亞. 中國特高壓交流輸電技術創新[J]. 電網技術,2013, 37(3): T1-T8.LIU Z Y. Innovation of UHVAC Transmission Technology in China[J]. Power System Technology, 2013, 37(3): T1-T8.

[3] 梅生偉, 朱建全. 智能電網中的若干數學與控制科學問題及其展望[J]. 自動化學報, 2013, 39(2): 119-131.MEI S W, ZHU J Q. Mathematical and Control Scientiflc Issues of Smart Grid and Its Prospects[J]. ACTA AUTOMATICA SINICA, 2013, 39(2): 119-131.

[4] B. Butrylo, F. Musy, L. Nicolas. A survey of parallel solvers for the finite element method in computational electromagnetics[J]. 2004, COMPEL Vol. 23 Iss 2pp. 531-546.

[5] 趙忠獻, 李鴻健, 豆育生. 并行矩陣乘的光化學反應模擬研究[J]. 軟件, 2010, 31(10): 16-20.ZHAO Z X, LI H J, DOU Y S. Research on parallel matrix multiplication Simulation of Photochemical Reactions[J].Software, 2010, 31(10): 16-20.

[6] 劉靜. 基于獨立生成樹的網絡多路徑傳輸方法研究[J]. 軟件, 2016, 37(4): 25-28.LIU J. Research on the Multi-path Transmission Method Based on Independent Spanning Tree[J]. Software, 2016,37(4): 25-28.

[7] 劉成軍. 基于消息傳遞接口的線性方程組并行計算研究[J].軟件, 2013, 34(1): 119-120.

[8] 唐萬和, 楊海東, 黎展滔, 等. 考慮能耗成本和拖期成本的非同等并行機調度[J]. 軟件, 2014, 35(3): 52-57.

[9] 曾晉, 呂韜. 一種基于零系數檢查的通道并行算法[J]. 軟件, 2014, 35(4): 153-156.

[10] 唐曼. 無線環境下基于多流優先級的并行多路傳輸[J]. 軟件, 2014, 35(10): 46-50.

[11] 武濤. 基于云計算的并行動態路徑搜索算法研究[J]. 軟件,2015, 36(4): 128-132.WU T. Research on Parallel Dynamic Path Search Algorithm Based on Cloud Computing[J]. Software, 2015, 36(4): 128-132.

[12] T. Oyama, T. Kitahara, Y. Serizawa. Parallel processing for power system analysis using band matrix[J]. IEEE TRANSACTION ON POWER SYSTEMS, 1990 Vol. 5 NO. 3 1010-1016.

[13] 周偉明. 多核計算與程序設計[M]. 武漢: 華中科技大學出版社, 2009.ZHOU W M. Multi-core Computing and Programming[M].Wuhan, China, Huazhong University of Science and Technology Press, 2009.

[14] The OpenMP API specification for parallel programming[EB/OL]. http://www.openmp. org/wp-content/uploads/openmp-4.5.pdf.2016.11.

[15] Leonardo D, Ramesh M. OpenMP: An Industry Standard API for Shared-Memory Programming[J]. IEEE Computational Science and Engineering, 1998, 5(1): 46-55.

[16] 鄒競, 馬華. 一種基于OpenMP的并行混合PVS算法[J]. 計算機應用研究, 2016, 33(1): 56-59, 91.ZOU J, MA H. Parallel hybrid PVS algorithm based on OpenMP[J]. Application Research of Computers, 2016, 33(1):56-59, 91.

[17] Q uinn M J. Parallel programming in C with MPI and OpenMP[M]. 北京. 清華大學出版社, 2005.

[18] 倪光正, 錢秀英. 電磁場數值計算(第2版)[M]. 北京: 機械工業出版社, 2010. 1.