KCCA-DPLS分布式建模算法研究

姚莉娟

(蘇州高等職業技術學校機電工程系，江蘇 蘇州 215011)

0 引言

隨著現代工業的不斷發展，生產過程復雜程度逐步加深,系統建模方法越來越多樣化。集中式建模控制方法[1-3]考慮了系統的整體性，但會出現模型結構相對復雜、模型精度難以保證和計算繁瑣等諸多問題。分散式建模方法降低了模型的復雜度[4-5]，但由于其沒有考慮到各子系統間的相互作用，系統的全局性無法得到滿足，分布式建模方法能較好地克服這些問題。本文提出了一種基于核典型相關分析(nuclear canonical correlation analysis,KCCA)和動態偏最小二乘(dynamic partial least squares，DPLS)的分布式建模方法。

胡蓓蓓等[6]提出了一種基于典型相關分析(canonical correlation analysis,CCA)[7]的系統分解方法。在分解過程中，該方法考慮了變量之間的關聯性。但該方法只針對線性系統。由于目前實際工業過程以非線性為主，所以本文采用KCCA對系統進行分解。分解前，將非線性過程線性化，分解后的子系統有多種建模方式。趙曌[8]采用偏最小二乘(partial least squares，PLS)進行建模，能夠降低大系統的維數，消除共線性。然而PLS只是純代數結構，無法應對實際工業過程中的動態性能。為了滿足動態系統的模型精度要求，更真實地描述系統的動態性能，本文采用DPLS方法[9]。該方法對分解后的關聯子系統進行動態建模，降低了系統的建模難度，同時提高了建模精度。

1 分布式建模算法描述

1.1 KCCA算法原理

KCCA是一種非線性數據分析算法[10-11]。數據集通過核函數進行隱式非線性映射，將輸入空間的非線性關系轉化為特征空間的線性關系，并通過核函數在核函數空間進行關聯分析。KCCA具有很強的線性擬合能力，其原理如圖1所示。

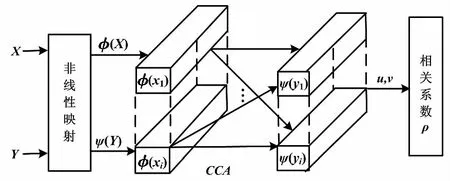
圖1 KCCA原理圖 Fig.1 Principle of KCCA

圖1中：φ(X)和φ(Y)分別為隨機變量組X和Y通過核函數，從觀測空間R映射到高維特征空間F的隱式映射。

(1)

則核函數為：

K(X,Y)=[φ(X),ψ(Y)]

(2)

建立線性CCA模型：

u=cTφ(X)
v=dTψ(Y)

(3)

式中：cT和dT為兩組投影向量，使得u和v的相關系數達到最大。

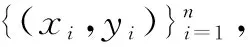
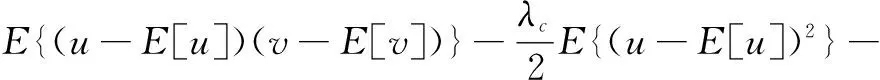
(4)

(5)

分別利用Lagrangian函數對c和d進行求導，可得：

(6)

式中：α和β分別為與高維空間中的權重c和d相對應的權重。

將式(6)代入式(3)，可得：

(7)

分別計算u和v的方差和協方差：

(8)

最后可以得到相關系數ρ：

(9)

式中：Kx=XXT;Ky=YYT。

使相關系數ρ達到最大值，求解如下優化問題：

(10)

根據Lagrangian函數，可得：

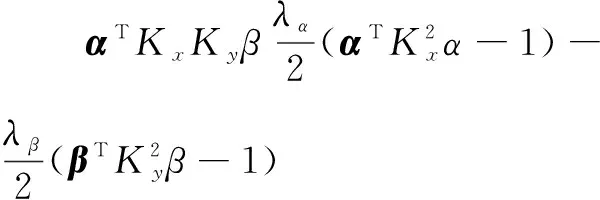
(11)

分別對α、β進行求導，可得：

(12)

由上式可得λ=λα=λβ，引入核函數后，得:

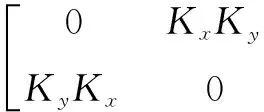
(13)

即：

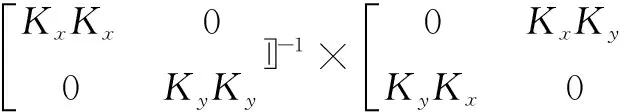
(14)

令：

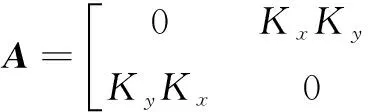
式(14)可化簡為：

B-1Aw=λw

(15)

只需求解B-1A的最大特征值λmax，即可得到α、β以及相關系數ρ。

1.2 DPLS建模算法原理

通過將ARX動態模型應用到PLS內模型的動態描述中，系統的輸入和輸出變量之間采用動態回歸的方式，形成一種動態建模算法。PLS內部模型采用的動態ARX模型形式為：

y=H(t)

(16)

DPLS建模流程如圖2所示。

圖2 DPLS建模流程圖 Fig.2 DPLS modeling process

圖2中：Wx和Wy為PLS建模之前的對角縮放矩陣；R為映射矩陣，將原始變量X轉換成得分向量t；Q為u的負載矩陣。

DPLS模型為：

(17)

系統的優化目標函數為：

(18)

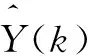
將N轉化為隱空間的優化目標函數：

(19)

式中：u(k)為k時刻隱變量空間中的實際輸出；uDPLS(k)為ARX-PLS內模型的輸出。

uDPLS=φ(k)θ(k)

(20)

φ(k)=[u(k-1),u(k-2),…,u(k-n),

t(k-1),t(k-2),…,t(k-m)]

θ(k)=[-a1(k),-a2(k),…,-an(k),

-b1(k),-b2(k),…,-bm(k)]T

(21)

式中：t(k)為當前時刻對應的輸入；φ(k)為輸入和輸出的當前及前一段時刻的信息；m和n為輸入向量、輸出向量維數；θ(k)為k時刻所建ARX模型的系統回歸參數。

將θ(k)代入式(18)中，可得優化目標函數為：

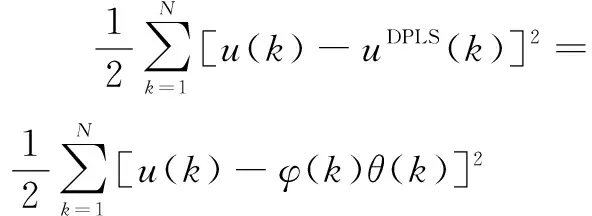
(22)

利用最小二乘(least squares,LS)辨識方法，可得：

θ(k)=[φT(k)φ(k)]-1φT(k)u(k)

(23)

將變量投影到PLS隱空間，逆矩陣求解時的病態問題得到了消除。

然后通過將內模型的輸出投影到原始空間，確定原始空間內系統的模型辨識誤差是否超過了允許的閾值ε，即：

(24)

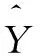
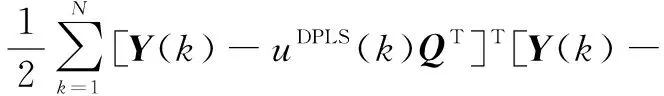
uDPLS(k)QT]≤ε

(25)

當輸出誤差超過了允許范圍(即E>ε)，則辨識過程被重新啟動，直到輸出誤差E≤ε。

模型更新流程如圖3所示。

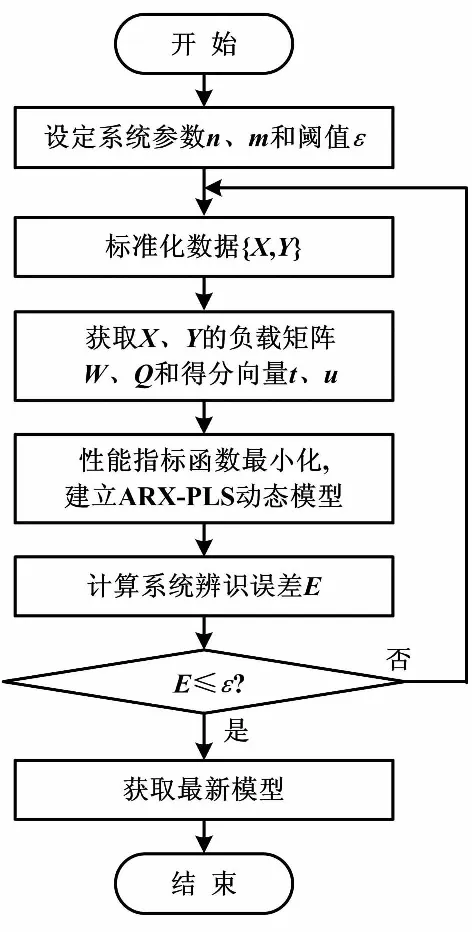
圖3 模型更新流程圖 Fig.3 Process of model updating

2 算法流程

KCCA和DPLS的分布式建模算法分為兩個階段：基于KCCA的非線性大系統分解和基于DPLS的各子系統動態建模。算法流程如下。

①分析工業過程質量指標，選擇與質量指標密切相關的關鍵變量作為輸入、輸出變量，采集相應的數據得到輸入變量集X和輸出變量集Y。

②對輸入輸出數據{X,Y}進行歸一化處理，利用KCCA方法得到各輸入變量、輸出變量間的權值系數ρ。

③設定門檻值ζi和ζj，選擇ρ大于等于門檻值ζi的輸入變量為子系統的獨立輸入變量，小于ζi且大于等于ζj的作為子系統的相互作用輸入變量，對大系統進行劃分，得到若干子系統。

④根據所分解后的子系統相應的輸入輸出變量，對每個子系統收集輸入輸出數據集{Xi,Yi}，采用ARX-PLS方法建模。

⑤確定原始空間內系統的模型辨識誤差E是否超過了允許的閾值ε。若在允許范圍內，則建模結束，否則返回步驟④。

根據上述步驟，得到基于KCCA和DPLS的分布式建模算法的基本結構如圖4所示。

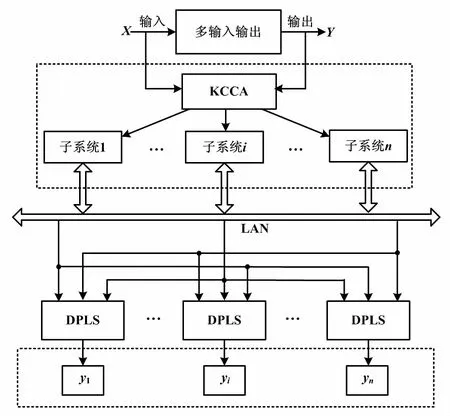
圖4 分布式建模算法結構圖 Fig.4 Structure of distributed modeling algorithm

3 試驗仿真

田納西-伊士曼(Tennessee-Eastman,TE)化工過程是一個基于實際化工過程的仿真模擬[11]，它滿足工業過程的非線性特點。TE過程由反應器、冷凝器、氣液分離器、汽提塔、循環壓縮機5個操作單元組成。4種氣態物進料分別為A、C、D和E(C中含有少量惰性氣體B)，經反應后生成G、H兩種主產物和副產品F。反應方程式如下：

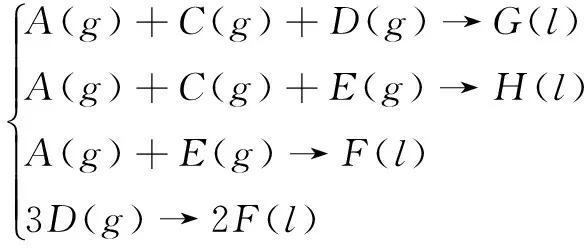
(26)

整個TE過程分為反應器溫度、氣液分離器溫度、G/H產率比3個子系統，相應的輸出變量分別為反應器溫度、氣液分離器溫度、G/H產率比。采用KCCA方法對上述過程進行系統分解。對所有變量數據，采用徑向基函數(radial basis function,RBF)進行非線性映射：

(27)

所有的變量通過RBF函數映射到KCCA空間，利用CCA建立線性模型，然后計算每個輸出變量與所有輸入變量的最大相關系數以及對應某輸入變量在特征提取時的權值系數。確定門檻值為0.5 和0.8,以此確定各子系統的變量。

采集的工業數據經處理后得到300個樣本點，取其中前150個樣本點作為建模訓練數據，后150個作為模型測試數據。對每個子系統分別采用DPLS算法和傳統PLS算法建立子模型進行比較。比較結果如圖5～圖7所示。AV為系統實際輸出值；PV為預測輸出值。

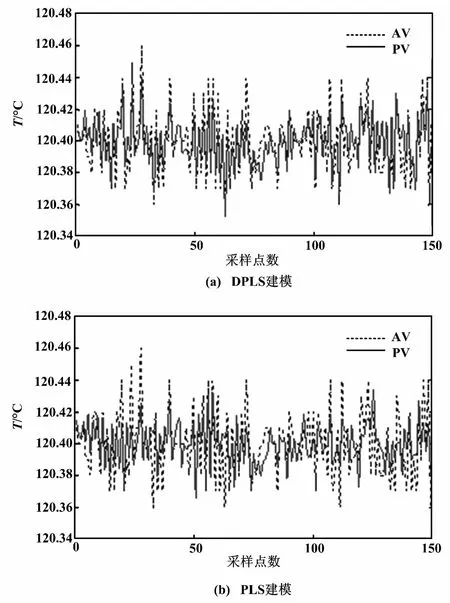
圖5 反應器溫度建模對比圖 Fig.5 Comparison of reactor temperature modelings

采用均方根誤差(root mean squared error,RMSE)和最大絕對誤差(maximum absolute error,MAXE),描述兩種建模方法的精度。

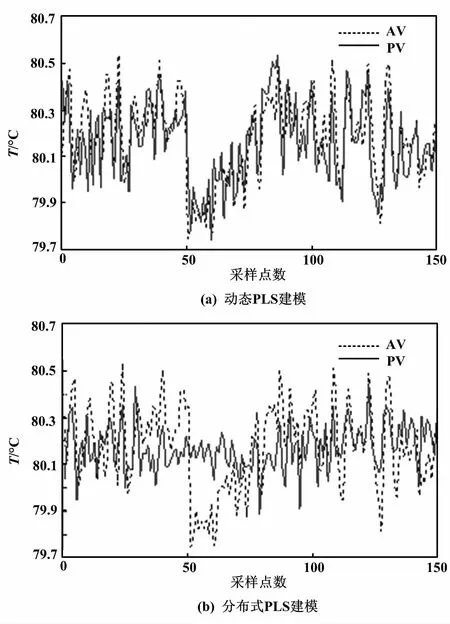
圖6 分離器溫度建模對比圖 Fig.6 Comparison of separator temperature modelings

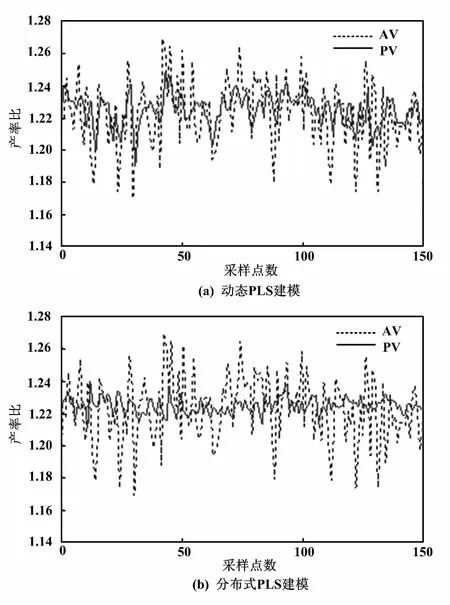
圖7 G/H 產率比建模對比圖 Fig.7 Comparison of G/H ratio modelings

(28)

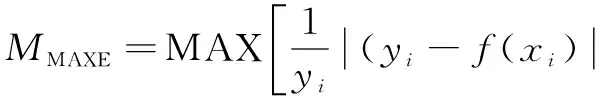
(29)

式中：yi為測試樣本的實際值；f(xi)為測試樣本的模型預測值；n為測試樣本數目。

RMSE、MAXE對比結果如表1所示。

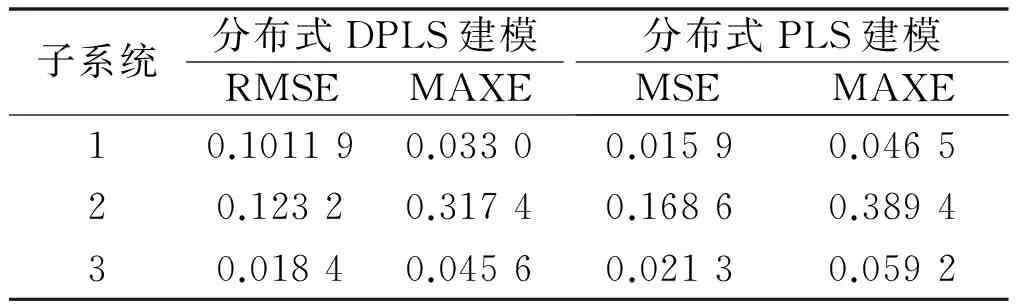
表1 RMSE、MAXE對比結果Tab.1 Comparison of RMSE、MAXE

傳統的PLS建模雖然簡化了模型結構，降低了計算難度，但這只是單純的數據結構模型，無法適應實際工業過程的動態性能，所以仿真效果較差。從RMSE和MAXE兩個性能指標的對比中可以看出，采用DPLS的分布式建模算法所建的模型精度更高。因此，分布式DPLS建模算法比傳統PLS建模方法更有優勢。

4 結束語

本文針對實際化工過程復雜多變、非線性強等特點，提出了一種KCCA和DPLS方法相結合的分布式建模算法。采用KCCA方法進行變量間的相關分析，將復雜的大系統分解為多個子系統。然后采用DPLS算法在隱空間得到子系統模型。通過對TE過程的仿真研究表明，所提出的算法降低了復雜大系統的模型維數，簡化了模型結構，滿足了非線性系統的模型需求，更好地適應模型的動態性能。同時，模型的精度也有了提高，系統的整體性能得到提升。但是本文對系統模型的穩定性還未作研究，這將是下一階段的研究重點。

參考文獻:

[1] RICCARDO SCATTOLINI.Architectures for distributed and hierarchical model predictive control-a review[J].Journal of Process Control,2009,19(5):723-731．

[2] RAVINDRA D,GUDI,AMES B.RAWLINGS.Identification for decentralized model predictive control[J].American Institute of Chemical Engineers,2006(52):2198-2210．

[3] BEN C,JURICE K,DALE E.Identificationof the tennessee eastman challenge process with subspace methods[J].Control Engineering Practice，2001,9(12):1337-1351．

[4] BRETT T.STEWAR T,ASWIN N,et al.Cooperative distributed model predictive control[J].Systems & Control Letters,2010,59(8):460-469．

[5] SAWADOGO S,FAYE R M,MALATERRE P,et al.Decentralized predictive controller for delivery canals[C]//Proceedings of the 1998 IEEE International on Systems，San Diego,USA,1998:3880-3884．

[6] 胡蓓蓓，李麗娟，熊路.基于相關分析與最小二乘支持向量機的TE過程多模型建模[J].計算機測量與控制，2015，23(1):60-63.

[7] 梁志平.多變量時間序列相關分析及建模預測研究[D].大連:大連理工大學,2010．

[8] 趙曌.基于PLS方法的建模及控制器設[D].杭州：浙江大學，2012.

[9] DONG Y N,QIN S.Dynamic-inner partial least squares for dynamic data modeling[J].IFAC-Papers On Line ,2015,48(8):117-122.

[10]李太福,易軍,蘇盈盈,等.基于KCCA虛假鄰點判別的非線性變量選擇[J].儀器儀表學報,2012,33(1):213-220.

[11]RICKER N L.Optimal teady-state operation of the Tennessee Eastman challenge process[J].Computers and Chemical Engineering,2005,19(9):949-959．