智能葉片風力機建模及多目標尾緣襟翼控制

張文廣， 白雪劍

(1．華北電力大學 新能源電力系統國家重點實驗室，北京 102206；2．華北電力大學 工業過程測控新技術與系統北京市重點實驗室，北京 102206)

隨著風力機的大型化發展，風力機葉片尺寸不斷增大，從而加劇了其疲勞載荷和極限載荷。為了更好地應對大型風力機葉片的不利載荷波動，智能葉片的概念應運而生。其中，尾緣襟翼技術通過改變翼型形狀來改變葉片氣動性能，具有響應快速，調節能力強等特點，被認為是目前最為可行的主動降載智能葉片技術[1]。

國內外學者對帶有尾緣襟翼的大型風力機智能葉片技術進行了研究。Hulskamp等[2]設計了一個直徑為1.8 m的帶有尾緣襟翼的風力機，并通過風洞實驗驗證了尾緣襟翼在降低葉片載荷方面的有效性。Castaignet等[3]在Vestas V27型風力機葉片上安裝了70 cm長的尾緣襟翼，實驗數據表明在1P頻率處葉片根部載荷的幅值減少了20%。盧經緯等[4]提出了帶有尾緣襟翼的風力機氣動經驗公式，并采用反步法設計了非線性控制器，仿真結果表明尾緣襟翼控制器可有效地穩定風力機輸出功率。但對于帶有尾緣襟翼的智能葉片風力機建模以及尾緣襟翼在主動降載和抑制功率波動的多目標控制，尚沒有詳細的研究。

因此，筆者基于NREL 5 MW參考風力機，在每個葉片上設計了2段獨立的尾緣襟翼，采用Matlab/Simulink搭建了帶有尾緣襟翼的智能葉片風力機模型，通過FAST氣彈仿真平臺對所建模型進行了對比驗證，并在此基礎上研究了多目標多襟翼控制器在主動降載和抑制功率波動方面的控制。

1 建模對象

以NREL 5 MW參考風力機為基礎，在每個葉片上增加2段獨立的尾緣襟翼，建立了帶尾緣襟翼的智能葉片風力機模型。

1.1 風力機參數

NREL 5 MW參考風力機為三葉片變速變槳型風力機，其主要參數見表1[5]。

1.2 尾緣襟翼

NREL 5 MW參考風力機葉片總長61.5 m，由8種翼型組成[5]，使用文獻[6]的最優尾緣襟翼參數，在每個葉片上增加2段獨立的尾緣襟翼，襟翼1位于第23～25葉素段上，襟翼2位于第26～29葉素段上。帶尾緣襟翼的葉片結構及襟翼1和襟翼2的位置如圖1所示。

2 智能葉片風力機建模

所建立的智能葉片風力機模型主要分為氣動模型、傳動鏈模型以及雙饋感應發電機模型。

表1 NREL 5 MW參考風力機參數

圖1 帶尾緣襟翼的NREL 5 MW參考風力機葉片結構圖

2.1 氣動模型

葉素動量理論是風力機空氣動力學的經典計算方法，具有計算速度快、精度高的特點。本文的氣動模型是在經典葉素動量理論基礎上，增加了尾緣襟翼角輸入量，并考慮葉尖損失修正和葛勞渥特修正，從而建立了帶尾緣襟翼的智能葉片風力機氣動模型。

2.1.1 葉素動量理論

葉素動量理論分為葉素理論和動量理論。葉素理論將葉片沿展向分為許多葉素，假設每個葉素上的空氣動力學特性相互獨立；動量理論是將包含風力機的環形控制體離散為多個環形單元控制體，假設控制體流體不可壓縮且相互獨立[7]。

葉素動量理論算法首先需要結合葉素與動量理論進行迭代計算，得出每個葉素上的局部載荷，迭代計算步驟如下。

(1)對軸向誘導因子a和切向誘導因子a′初始化，取a=a′=0。

(2)計算入流角φ：

(1)

式中：v0為入流風速；ω為葉輪轉速；r為葉素局部半徑。

(3)計算局部攻角α：

α=φ-θ

(2)

式中：θ為局部槳距角，θ=(θp+β)，其中θp為槳距角，β為葉素扭角。

(4)采用線性插值法從翼型數據表中求得升力系數Cl(α)和阻力系數Cd(α)。

(5)計算法向力系數Cn和切向力系數Ct：

Cn=Clcosφ+Cdsinφ

(3)

Ct=Clsinφ-Cdcosφ

(4)

(6)引入普朗特葉尖損失因子F，計算軸向誘導因子a和切向誘導因子a′：

(5)

(6)

(7)引入a值較大的葛勞渥特修正：

(7)

式中：CT為推力系數。

(8)判斷a與a′的變化值是否大于0.01，若大于0.01，返回第(2)步，否則計算完成。

葉素局部法向載荷pN和局部切向載荷pT計算式如下：

(8)

(9)

則葉片上的切向力矩MT和法向力矩MN分別為：

(10)

(11)

由式(10)和式(11)可得葉輪轉矩Mr、葉輪功率PAero、功率系數Cp和葉片揮舞方向彎矩Mflap為：

(12)

PAero=Mr·ω

(13)

(14)

Mflap=MNcosθp-MTsinθp

(15)

2.1.2 尾緣襟翼角的引入

對于所設計的帶尾緣襟翼的翼型，升力系數Cl和阻力系數Cd隨著攻角α和襟翼角γ的變化而變化。

采用Xfoil軟件[8]，在NACA64_A17翼型的基礎上，改變尾緣偏轉角，得到不同尾緣襟翼角γ的翼型，并對翼型進行氣動分析計算，得到上述尾緣襟翼翼型的升力系數Cl和阻力系數Cd隨攻角α變化的數據表。整理后得到Cl(α,γ)和Cd(α,γ)的二維數據表，則不同攻角α和襟翼角γ下的Cl(α,γ)和Cd(α,γ)可以通過線性插值法查表得到。

2.2 傳動鏈模型

風力機的傳動系統可以看成是由有限個慣性單元、彈性單元和阻尼單元組成的。因此，在建立傳動鏈模型時，可以采用彈簧-阻尼-質量系統作為動力學模型[9]。通過有選擇地考慮傳動軸的柔性和旋轉部分的慣量，將傳動鏈模型分為單質塊模型、雙質塊模型和三質塊模型[10]。

與風輪轉子和發電機的轉動慣量相比，齒輪箱的轉動慣量很小，筆者參考FAST氣彈仿真平臺[11]，傳動鏈模型采用雙質塊模型，忽略了齒輪箱轉動慣量，考慮了低速軸的柔性和阻尼特性，并視高速軸為剛性。

根據圖2，風輪轉子和低速軸的運動方程：

(16)

(17)

齒輪箱的運動方程：

TL=N·TH

(18)

θL=θH/N

(19)

高速軸和發電機的運動方程：

θH=θG

(20)

(21)

式中：Jr為風輪轉子轉動慣量；JG為發電機轉動慣量；θr為風輪轉子角位移；θL為低速軸角位移；θH為高速軸角位移；θG為發電機角位移；Tr為風輪轉子氣動扭矩；TL為低速軸扭矩；TH為高速軸扭矩；TG為發電機的電磁轉矩；K為低速軸剛度；C為低速軸阻尼；N為齒輪箱傳動比。

圖2 雙質塊傳動鏈模型等效圖

2.3 雙饋感應發電機模型

雙饋感應發電機又稱轉子交流勵磁電機，主要包括電機本體和交流勵磁及控制系統2部分。所使用的雙饋感應發電機是在Simulink中雙饋異步發電機的基礎上，通過修改其內部結構[12]和發電機參數[13]，并調整其矢量控制的控制器參數，得到額定功率為5 MW的雙饋感應發電機模型(見圖3)。

圖3 5 MW風力機雙饋感應發電機模型

3 智能葉片風力機模型驗證

FAST是由NREL開發的氣彈仿真平臺，可計算兩葉片或三葉片水平軸風力機的極端載荷和疲勞載荷[14]，其經過GL認證，計算結果準確度高。針對無襟翼和有襟翼的情況，采用基于FAST的帶尾緣襟翼的風力機氣彈仿真平臺[6]對所建立的智能葉片風力機模型進行對比驗證。

3.1 4～11 m/s階躍變化風況對比

仿真時間為800 s，仿真風況為每100 s增加1 m/s的階躍變化風況，變化范圍為4～11 m/s。圖4給出了輪轂高度風速從4 m/s到11 m/s階躍增加時，智能葉片風力機模型與FAST氣彈仿真平臺的對比圖。從圖4可以看出，與FAST氣彈仿真平臺相比，智能葉片風力機模型葉片1葉根揮舞彎矩偏差小于4.6%，發電機轉速偏差小于0.2%，發電機功率偏差小于0.5%。可見，在4～11 m/s的階躍變化風況下，所建立的智能葉片風力機模型精度較高。

(a)葉片1葉根揮舞彎矩

(b)發電機轉速

(c)輸出功率

3.2 11～24 m/s階躍變化風況對比

仿真時間為1 400 s，仿真風況為每100 s增加1 m/s的階躍變化風況，變化范圍為11～24 m/s。圖5給出了輪轂高度風速從11 m/s到24 m/s階躍增加時，智能葉片風力機模型與FAST氣彈仿真平臺的對比圖。從圖5可以看出，與FAST氣彈仿真平臺相比，智能葉片風力機模型葉片1葉根揮舞彎矩偏差小于9.4%，變槳角偏差小于0.8%，發電機轉速偏差小于0.2%，發電機功率偏差小于1.5%。可見，在11～24 m/s階躍變化風況下，所建立的智能葉片風力機模型精度較高。

3.3 平均風速為11.4 m/s時標準湍流風況對比

仿真時間為300 s，仿真風況為輪轂高度平均風速為11.4 m/s，湍流強度為5%的標準湍流風況。

(a)葉片1葉根揮舞彎矩

(b)葉片1變槳角

(c)發電機轉速

(d)發電機輸出功率

圖6給出了輪轂高度平均風速為11.4 m/s的標準湍流風況下，智能葉片風力機模型與FAST氣彈仿真平臺的對比圖。從圖6可以看出，與FAST氣彈仿真平臺相比，智能葉片風力機模型葉片1葉根揮舞彎矩偏差小于2.4%，變槳角偏差小于3.4%，發電機轉速偏差小于0.3%，發電機功率偏差小于0.3%。因此，在標準湍流風況下，所建立的智能葉片風力機模型精度較高。

3.4 15 m/s穩定風況下變槳及襟翼控制對比

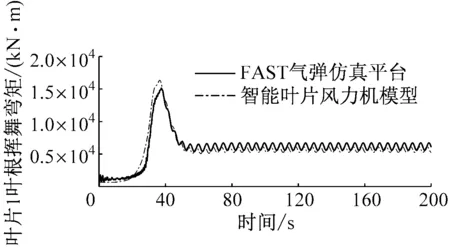
仿真時間為200 s，仿真風況為輪轂高度風速為15 m/s的穩定風況。對每個葉片上的2個襟翼采用相同的獨立襟翼控制方法[15]。

圖7給出了輪轂高度風速為15 m/s的穩定風況下，智能葉片風力機模型與FAST氣彈仿真平臺的對比圖。從圖7可以看出，智能葉片風力機模型與FAST氣彈仿真平臺相比，無襟翼控制時，葉片1葉根揮舞彎矩偏差小于7.3%，變槳角偏差小于0.4%；有襟翼控制時，葉片1葉根揮舞彎矩偏差小于9.2%，變槳角偏差小于3.1%，襟翼角在100～200 s的平均偏差小于0.1%。因此，在變槳及襟翼控制方面，智能葉片風力機模型精度較高。對比圖7(a)～圖7(d)可以看出，有襟翼控制時，葉片1的葉根揮舞彎矩波動幅度明顯減小，其變槳角也明顯減小。

(a)葉片1葉根揮舞彎矩

(b)葉片1變槳角

(c)發電機轉速

(d)發電機輸出功率

從以上4種風況的對比情況可以看出，與FAST氣彈仿真平臺相比，智能葉片風力機模型在整個風力機工作范圍的穩定風況以及湍流風況下，葉片1的葉根揮舞彎矩偏差小于9.4%，發電機轉速偏差小于0.3%，發電機功率偏差小于1.5%，葉片1的變槳角偏差小于3.4%，葉片1的襟翼角偏差小于0.1%。說明所建立的智能葉片風力機模型對風力發電過程的仿真具有較高精度，計算結果具有較高的可信性。

(a)無襟翼控制時葉片1葉根揮舞彎矩

(b)有襟翼控制時葉片1葉根揮舞彎矩

(c)無襟翼控制時葉片1變槳角

(d)有襟翼控制時葉片1變槳角

(e)有襟翼控制時葉片1襟翼角

4 多目標的多襟翼控制

更靠近葉尖的尾緣襟翼能更有效地減少葉根載荷，對功率的影響也更小[16]。為了更好地發揮尾緣襟翼在降載及抑制功率波動方面的作用，采用圖1所示的襟翼1控制發電機的功率波動，襟翼2控制葉根揮舞彎矩。

襟翼1采用PID方法(PID1)來控制襟翼偏轉角，從而抑制發電機功率產生的波動；襟翼2采用PID方法(PID2)來控制襟翼角的周期性變化，以減少葉根揮舞彎矩產生的周期性波動。因此，襟翼1和襟翼2控制器之間耦合作用較弱，可忽略相互間的影響。PID1的反饋信號為發電機轉速，設定值為當前控制時刻前20 s的發電機轉速平均值；PID2采用獨立襟翼控制器[15]，反饋信號為葉根揮舞彎矩的偏航和俯仰分量，設定值為0。

在輪轂高度平均風速為11.4 m/s的湍流風況下進行仿真，在80 s加入襟翼2控制，100 s加入襟翼1控制，并與無襟翼的仿真結果進行對比，選取第150～250 s的數據進行分析，結果見表2。葉片1葉根揮舞彎矩標準差、葉片1葉根揮舞彎矩1P處功率譜密度、發電機轉速標準差和發電機功率標準差的變化率分別為-18.26%、-89.73%、-74.65%和-75.07%。

表2 標準湍流風況下有無襟翼控制的風力機參數對比

圖8給出了標準湍流風況葉片1葉根揮舞彎矩及其功率譜密度。由圖8可知，多目標多襟翼控制下，葉根揮舞彎矩的振蕩明顯減弱，特別是在1P頻率，即0.2 Hz處，葉根揮舞彎矩的功率譜密度有明顯降低。其標準偏差減少了18.26%，1P頻率處的功率譜密度減少了89.73%。說明在標準湍流風況下，多目標多襟翼控制可有效降低葉片的疲勞載荷。

(a)葉片1葉根揮舞彎矩

(b)葉片1葉根揮舞彎矩的功率譜密度

圖9和圖10分別為標準湍流風況下風力機的發電機轉速和高速軸功率。由圖9、圖10可知，在多目標多襟翼控制作用下，風力機發電機轉速和發電機功率波動明顯減小，其標準偏差分別減少74.65%和75.07%。說明多目標多襟翼控制使風力機功率輸出更平滑，從而使風電場的出力更平穩，更利于電網接納風電。

圖9 標準湍流風況風力機發電機轉速

圖10 標準湍流風況風力機高速軸功率

圖11給出了標準湍流風況下葉片1的襟翼角。由圖11可知，在多目標多襟翼控制作用下，襟翼2在PID2作用下進行周期性擺動控制，幾乎不受襟翼1的PID1控制影響。這也說明了2個襟翼控制器之間耦合關系較弱，可獨立進行控制。

圖11 標準湍流風況葉片1的襟翼角

5 結 論

(1)在整個風力機工作范圍內穩定風況以及輪轂平均風速為11.4 m/s的標準湍流風況下，將所建立的智能葉片風力機模型葉片1的葉根揮舞彎矩、變槳角和襟翼角以及發電機轉速、發電機功率這5個參數與FAST氣彈仿真平臺中的相應參數進行對比，結果表明所建立的智能葉片風力機模型對風力機發電過程的仿真精度較高，計算結果具有一定的可信度。

(2)在標準湍流風況下，多目標多襟翼控制不僅可以大幅減小葉根揮舞彎矩在1P頻率處的幅值，而且可以有效減弱發電機轉速的波動，平滑風力機輸出功率。這說明多目標多襟翼控制不僅可以顯著降低葉片的疲勞載荷，延長風力機壽命，而且可以抑制風力機輸出功率波動，顯著改善智能葉片風力機并網對電網的影響，具有一定的實際參考價值。

參考文獻：

[1] COUCHMAN I, CASTAIGNET D, POULSEN N K, et al. Active load reduction by means of trailing edge flaps on a wind turbine blade[C]//Proceedingsof2014AmericanControlConference. Portland, USA: IEEE, 2014: 3722-3727.

[2] HULSKAMP A W, van WINGERDEN J W, BARLAS T, et al. Design of a scaled wind turbine with a smart rotor for dynamic load control experiments[J].WindEnergy, 2011, 14(3): 339-354.

[3] CASTAIGNET D, BARLAS T, BUHL T, et al. Full-scale test of trailing edge flaps on a Vestas V27 wind turbine: Active load reduction and system identification[J].WindEnergy, 2014, 17(4): 549-564.

[4] 盧經緯, 張臻, 梁宇坤, 等. 具有尾緣襟翼風力機的恒功率反步法控制[J].控制理論與應用, 2017, 34(1): 61-68.

LU Jingwei, ZHANG Zhen, LIANG Yukun, et al. Backstepping control of constant power for wind turbines with trailing edge flaps[J].ControlTheory&Applications, 2017, 34(1): 61-68.

[5] JONKMAN J, BUTTERFIELD S, MUSIAL W, et al. Definition of a 5-MW reference wind turbine for offshore system development[R]. Colorado: National Renewable Energy Laboratory, 2009.

[6] 張文廣, 白雪劍, 韓越. 風力機尾緣襟翼結構參數優化及控制性能分析[J].動力工程學報, 2017, 37(12): 1023-1030.

ZHANG Wenguang, BAI Xuejian, HAN Yue. Trailing edge flap structure parameters optimization of a wind turbine and analysis of the control performance[J].JournalofChineseSocietyofPowerEngineering, 2017, 37(12): 1023-1030.

[7] HANSEN M O L. Aerodynamics of wind turbines[M]. 2nd ed. Oxford, UK: Earthscan, 2008: 45-57.

[8] DRELA M, YOUNGREN H. XFOIL 6.9 user primer[EB/OL]. [2016-11-01]. http://web.mit.edu/drela/Public/web/xfoil/xfoil_doc.txt.

[9] 劉豹. 風力發電機傳動裝置建模分析[D]. 沈陽: 東北大學, 2012.

[10] 劉吉臻. 新能源電力系統建模與控制[M]. 北京: 科學出版社, 2015.

[11] JONKMAN B, JONKMAN J. Resistant moment of the rotor and of the electric generator[EB/OL]. [2017-01-10]. https://wind.nrel.gov/forum/wind/viewtopic.php?f=2&t=525.

[12] SINGH M, MULJADI E, JONKMAN J, et al. Simulation for wind turbine generators-with FAST and MATLAB-Simulink modules[R]. USA: NREL, 2014.

[13] WU Bin, LANG Yongqiang, ZARGARI N, et al. Power conversion and control of wind energy systems[M]. Hoboken,USA: Wiley-IEEE Press, 2011.

[14] JONKMAN J M, BUHL JR M L. FAST user's guide-updated august 2005[R]. USA: NREL, 2005.

[15] AQUINO B B. New generator control algorithms for smart-bladed wind turbines to improve power capture in below rated conditions[D]. Amherst,USA: University of Massachusetts-Amherst, 2014.

[16] 張文廣, 李騰飛, 劉吉臻, 等. 尾緣襟翼結構參數對大型風機氣動性能影響的仿真研究[J].可再生能源, 2016, 34(12): 1826-1833.

ZHANG Wenguang, LI Tengfei, LIU Jizhen, et al. Simulation study on trailing edge flaps' structure parameters affecting aerodynamic performance of large wind turbines[J].RenewableEnergyResources, 2016, 34(12): 1826-1833.