追本求“圓” 剖析本質

顧嘯敏

“圓”的相關知識覆蓋面較大，要求我們不僅能掌握圓的基本知識，而且能綜合運用圓與直線型圖形的知識來解決相關問題.

一、知識網絡

二、要點剖析

1.與圓有關的概念.

（1）圓的概念中圓心決定圓的位置，半徑決定圓的大小.

（2）直徑是圓中最長的弦，弦不一定是直徑，判斷一條弦是否是直徑關鍵是看弦是否經過圓心；半圓是弧，弧不一定是半圓.

（3）對等弧的認識要注意關鍵詞：能夠重合.

例1 （2017·隨州）如圖1，已知AB是⊙O的弦，半徑OC垂直AB，點D是⊙O上一點，且點D與點C位于弦AB兩側，連接AD、CD、OB，若∠BOC=70°，則∠ADC=_______°.

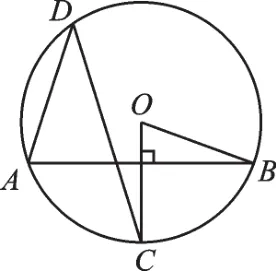
圖1

2.與圓有關的角.

圓心角與圓周角：頂點在圓心的角叫做圓心角；頂點在圓上，并且兩邊都和圓相交的角叫做圓周角.

例2 （2017·揚州）如圖2，已知⊙O是△ABC的外接圓，連接AO，若∠B=40°，則∠OAC=_______°.

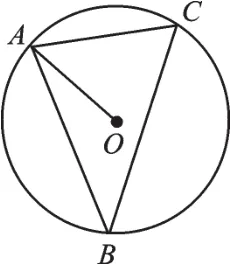
圖2

【解析】根據“同弧所對的圓周角等于它所對圓心角的一半”，連接OC，便有∠AOC=2∠B=80°，再由OA=OC，根據“等邊對等角”及“三角形內角和定理”可以求得∠OAC=50°.

例3 （2017·淮安）如圖3，在圓內接四邊形ABCD中，若∠A、∠B、∠C的度數之比為4∶3∶5，則∠D的度數是______ °.

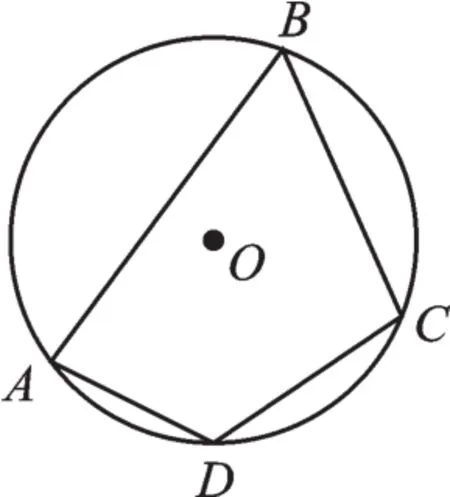
圖3

【解析】因為四邊形ABCD是⊙O的內接四邊形，所以∠A+∠C=∠B+∠D=180°.因為∠A、∠B、∠C的度數之比為4∶3∶5，所以∠A、∠B、∠C、∠D 的度數之比為 4∶3∶5∶6，所以∠D=120°.

3.與圓的對稱性有關的兩個定理：圓心角、弧、弦關系定理和垂徑定理.

這兩個定理分別從圓的旋轉不變性和圓的軸對稱性中獲得.因此，抓住對稱是解決問題的關鍵.

例4 （2017·眉山）如圖4，AB是⊙O的弦，半徑OC⊥AB于點D，且AB=8cm，DC=2cm，則OC=______ cm.

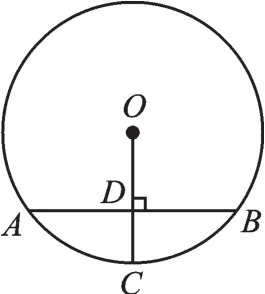
圖4

【解析】連接OA，由垂徑定理易知AD=4，設⊙O的半徑為x，在Rt△OAD中，OA2=OD2+AD2，即x2=（x-2）2+42，解得x=5，所以OC=5.

4.與圓有關的位置關系.

判斷點或直線與圓的位置關系，往往需要比較數量關系，即通過比較點和圓心的距離與半徑的大小關系來判斷點與圓的位置關系，通過比較圓心和直線的距離與半徑的大小關系來判斷直線與圓的位置關系.

例5 （2017·自貢）AB是⊙O的直徑，PA切⊙O于點A，PO交⊙O于點C,連接BC，若∠P=40°，則∠B等于_____ °.

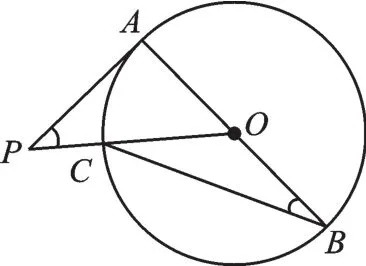
圖5

【解析】由切線的性質知∠PAO=90°.從而易得∠POA=50°，再由圓周角與圓心角關系得∠B=25°.

5.三角形的外心與內心.

外心是三角形外接圓的圓心，是三邊垂直平分線的交點，它到三角形三個頂點的距離相等；內心是三角形內切圓的圓心，它是三條角平分線的交點，它到三角形三邊的距離相等.

例6 （2017·泰州）如圖6，在平面直角坐標系xOy中，點A、B、P的坐標分別為（1，0），（2，5），（4，2），若點C在第一象限內，且橫坐標、縱坐標均為整數，P是△ABC的外心，則點C的坐標為________ .

圖6

【解析】如圖6，以點P為圓心，PA為半徑作圓，⊙P在第一象限經過的符合條件的點有3個，分別是（7，4），（6，5），（1，4）.故答案為（7，4），（6，5），（1，4）.

6.正多邊形和圓.

正多邊形與圓的關系：將圓n（n≥3）等分，依次連接各分點所得的多邊形是這個圓的內接正多邊形，這個圓叫做正多邊形的外接圓，其實這種關系也給出了畫多邊形的作圖方法.

【剖析】正多邊形的定義包括兩個相等，即各邊相等，各角也相等，兩者缺一不可.

例7 （2017·濱州）若正方形的外接圓半徑為2，則其內切圓半徑為（ ）.

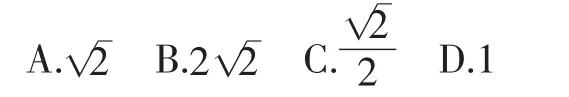
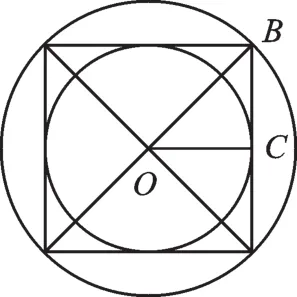
圖7

【解析】如圖7，由“正方形的外接圓半徑為2”可得OB=2，∠OBC=45°，由切線性質可得∠OCB=90°，所以△OBC為等腰直角三角形，所以OC=2.故選A.

7.弧長、扇形面積、圓錐的側面積.

弧長、扇形面積、圓錐的側面積以及全面積的計算公式不要求死記硬背，關鍵是要理解記憶，圓心角是周角的幾分之幾，則弧長就是圓周的幾分之幾，扇形面積就是圓面積的幾分之幾；對于扇形面積公式，相當于把半徑是R，弧長是l的扇形近似看成一個底是l，高是R的三角形來記憶.在計算圓錐的側面積和全面積時要注意圓錐的母線、圓錐的高、圓錐的底面半徑構成直角三角形，可以利用勾股定理得出三者的關系.

例8 （2017·自貢）圓錐的底面周長為6πcm，高為4cm，則該圓錐的全面積是_______；側面展開扇形的圓心角是______ °.

【解析】圓錐的底面周長為6π，∴底面半徑為r=6π÷2π=3，根據勾股定理，得圓錐的母線，側面展開扇形的弧長l=2πr=6π，∴側面展開扇形的面積6π×5=15π，底面積S底=πr2=9π，∴該圓錐的全面積S全=15π+9π=24π.

例9 （2017·南充）如圖8，在Rt△ABC中，AC=5cm，BC=12cm，∠ACB=90°，把Rt△ABC繞BC所在的直線旋轉一周得到一個幾何體，則這個幾何體的側面積為（ ）.

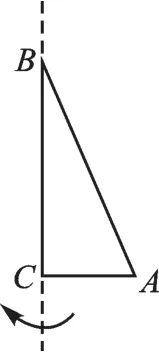
圖8

A.60πcm2B.65πcm2

C.120πcm2D.130πcm2

【解析】由勾股定理可求得AB=13.這個幾何體是圓錐，圓錐的底面半徑AC=5，母線AB=13，圓錐的側面積=πAC·AB=π×5×13=65π.故選B.

三、疑難突破

1.巧作輔助線，化難為易.

運用垂徑定理時常常需過圓心作弦的垂線段，利用半徑、弦心距和弦的一半組成的直角三角形來求解.證明直線和圓相切，一般有兩種情形：（1）已知直線與圓有公共點時，連接圓心與公共點的半徑，證明該半徑與已知直線垂直；（2）當已知直線與圓公共點不明確時，那就過圓心作與已知直線的垂線段，證明垂線段和半徑相等.

2.關注圓中的兩解問題.

注意弦所對的弧有優劣之分，因此弦所對的圓周角就有兩個，這兩個圓周角互補.

3.轉化思想在圓中的應用.

在圓中轉化思想多體現在把圓的問題轉化為直線型的問題，把弧的問題轉化為角或弦的問題等.