巧添圓 妙解題

汪國銀

通過挖掘題目中的隱含條件，恰當(dāng)?shù)貥?gòu)造輔助圓，我們能夠巧妙地解決一些看似復(fù)雜的直線型問題.構(gòu)造輔助圓解題的關(guān)鍵是要善于發(fā)現(xiàn)隱含于題中與圓有關(guān)的信息，抓住題目的特征，進而拓寬解題思路.

一、依據(jù)圓的定義，添加輔助圓

例1 如圖1，若AB=OA=OB=OC，則∠ACB的大小是（ ）.

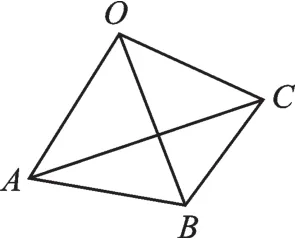
圖1

A.40° B.30° C.20° D.35°

【分析】從表象上看，本道題是普通的直線形問題，而事實上圖中角與角之間的關(guān)系比較復(fù)雜，解答的難度很大.如果由條件OA=OB=OC聯(lián)想到圓的定義，以點O為圓心，以O(shè)A長為半徑作圓，問題便迎刃而解了.

【解析】如圖2，以點O為圓心，以O(shè)A長為半徑作圓.

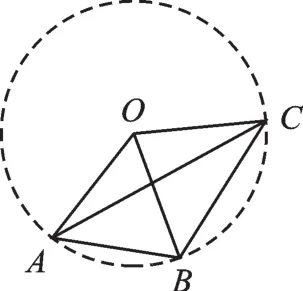
圖2

∵AB=OA=OB，

∴△ABO是等邊三角形，

∴∠AOB=60°，

【點評】當(dāng)遇有公共端點的等線段長時，我們通常以公共端點為圓心，等線段長為半徑，構(gòu)造輔助圓.

二、從圓的性質(zhì)入手，構(gòu)造輔助圓

圓的性質(zhì)主要集中在圓周（心）角、弧、弦（直徑）等對象之間的相互關(guān)系上，因此在解決有關(guān)角、線之間的問題時，我們可考慮添加輔助圓，運用圓的性質(zhì)尋找解題的方法.

1.從圓周角“動而不變”的特征入手.

例2 如圖3，在△ABC中，AB=2，∠C=30°，則△ABC的面積最大值為______.

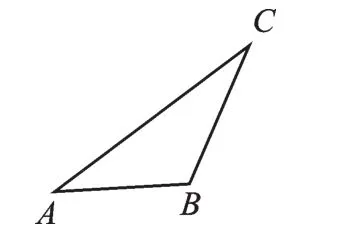
圖3

【分析】因為△ABC的底AB=2為定值，所以要使△ABC的面積取最大值，需滿足AB邊上的高最大（即點C到AB的距離最大），而條件“∠C=30°”表明“∠C的頂點位置改變，但大小不變”，根據(jù)這一特性，我們可以作△ABC的外接圓，當(dāng)AB邊上的高CD經(jīng)過圓心O時，高CD最大，因而△ABC的面積最大值.

【解析】如圖4，作△ABC的外接圓，當(dāng)高CD經(jīng)過圓心O時△ABC的面積最大.

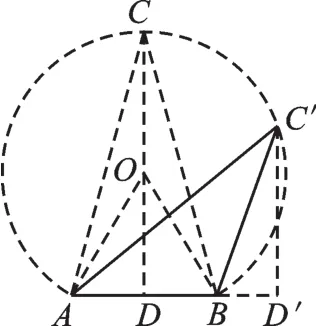
圖4

連接OA、OB，

∵∠C=30°，

∴∠AOB=60°，

∵OA=OB，OD⊥AB，

∴OD=AD·tan60°=3，

∴CD=CO+OD=2+3，

故答案為2+ 3.

【點評】挖掘題中隱藏的某個角具有“頂點位置改變而其大小不變，即‘動而不變’”這一特性，據(jù)此添加合適的輔助圓來解決問題.

2.從直角與直徑之間的關(guān)系入手，巧添輔助圓.

例3 如圖5，在等腰三角形ABC中，∠ABC=90°，AB=BC=2，P是△ABC所在平面內(nèi)一點，且滿足PA⊥PB，則PC的取值范圍為______.

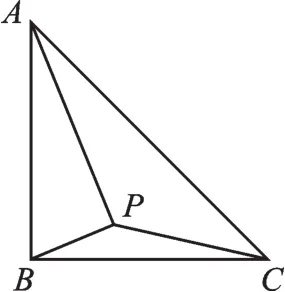
圖5

【分析】根據(jù)條件可知線段AB是定值且AB所對的張角∠APB是90°，根據(jù)直徑所對圓周角為直角可知，動點P的運動軌跡在過點A、B、P三點的圓周上（不與A、B重合），設(shè)AB中點為O，連接CO并延長，分別交圓O為P1、P2，P的位置在P1處最小，P2處最大，據(jù)此求解可得.

【解析】∵PA⊥PB，即∠APB=90°，AB=BC=2，

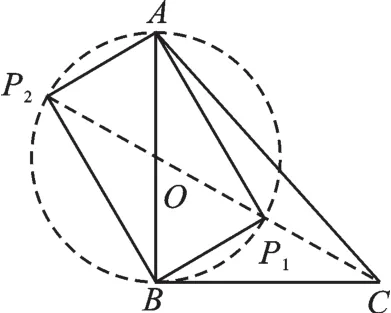
圖6

∴點P在以AB為直徑、AB的中點O為圓心的O上，如圖6，連接CO交⊙O于點P1，延長CO交⊙O于點P2，CO=，由圖可知，P1C≤PC≤P2C.

∴ 5-1≤PC≤ 5+1.

【點評】利用90°的圓周角所對的弦是直徑，以斜邊為直徑，構(gòu)造輔助圓.

3.從四邊形對角都是90°或?qū)腔パa入手.

例 4 如圖 7，在 Rt△ABC 中，∠A=90°，AB=6，AC=8，點D為邊BC的中點，點M為邊AB上的一動點，點N為邊AC上的一動點，且∠MDN=90°，則cos∠DMN為（ ）.

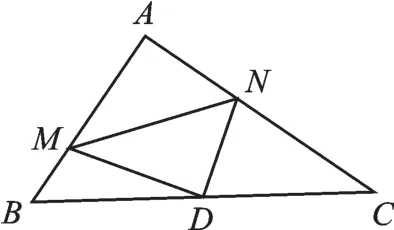
圖7

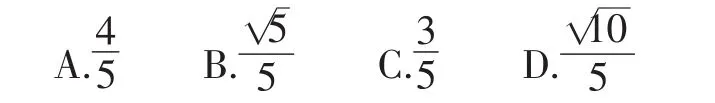
【分析】線段MN所對的∠MAN、∠MDN都等于90°，且∠MAN+∠MDN=180°，聯(lián)想到“圓的內(nèi)接四邊形的對角互補”，構(gòu)造以MN為直徑的圓，則可證點A、M、D、N四點共圓，連接AD，易證∠DMN=∠DAN=∠C，問題便迎刃而解.

【解析】如圖，連接AD，

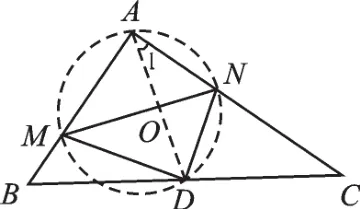
圖8

∵∠A=90°，AB=6，AC=8，

∵點D為邊BC的中點，

∴DA=DC=5，

∴∠1=∠C，

∵∠MDN=90°，∠A=90°，

∴點A、D在以MN為直徑的圓上，

∴∠1=∠DMN，

∴∠C=∠DMN，

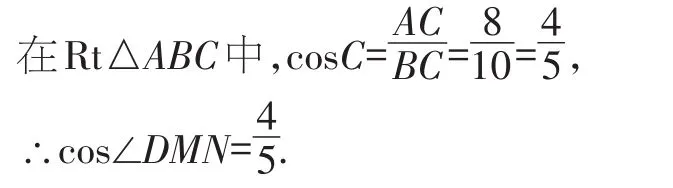
故選A.

【點評】利用構(gòu)造輔助圓解決問題，有助于我們很快找到符合要求的線段或角，使問題得到巧妙解決.