規范答題,提高考試成績
何廣謀

2017年的中考已落下帷幕,從答題情況來看,特別是解答題,不少同學出現了會做的題目做不對,解對的題目寫不全的現象,從而丟掉了一定的分數,這不能不讓人感到遺憾.針對這種情況,本人結合2017年中考命題的經驗和“圓”這一章節相關知識點,列舉典型的、有代表性的中考題來說明如何規范答題.
和“圓”相關的解答題在數學中考當中的分值一般為10分的中檔題或者12分的綜合題,下面我就以這兩個分值的題舉例說明.
類型一:10分的中檔題
1.設計有兩個問題的.
例1 (2017·阿壩州)如圖1,在△ABC中,∠C=90°,點O在AC上,以OA為半徑的⊙O交AB于點D,BD的垂直平分線交BC于點E,交BD于點F,連接DE.
(1)判斷直線DE與⊙O的位置關系,并說明理由;
(2)若 AC=6,BC=8,OA=2,求線段 DE的長.
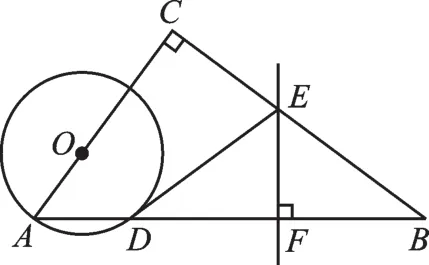
圖1
【分值猜想】本道題有兩個問題,一個證明一個計算,既考查說理又考查計算能力是一種常見的組合方式,這樣的10分題通常每問5分.
【考點】直線與圓的位置關系;線段垂直平分線的性質.
【分析】(1)直線DE與圓O相切,理由如下:連接OD,由OD=OA,利用等邊對等角得到一對角相等,等量代換得到∠ODE為直角,即可得證;(2)連接 OE,設DE=x,則 EB=ED=x,CE=8-x,在直角三角形OCE中,利用勾股定理列出關于x的方程,求出方程的解得到x的值,即可確定出DE的長.
【解答】(1)直線DE與⊙O相切.(1分)
理由:連接OD,
∵OD=OA,∴∠A=∠ODA,
∵EF是BD的垂直平分線,
∴EB=ED,∴∠B=∠EDB,
∵∠C=90°,∴∠A+∠B=90°,
∴∠ODA+∠EDB=90°,
∴∠ODE=180°-90°=90°,
∴直線DE與⊙O相切.(5分)
(2)連接OE,
設DE=x,則EB=ED=x,CE=8-x,
∵∠C=∠ODE=90°,
∴OC2+CE2=OE2=OD2+DE2,
∴42+(8-x)2=22+x2,(8分)
解得:x=4.75,
則DE=4.75.(10分)
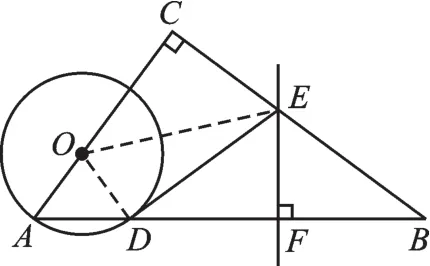
圖2
【注意】通常情況下,像第一問中判斷直線與圓的位置關系這樣的問題,只要回答正確也是能得1分的,所以同學們千萬不要忽視.
2.設計有3個問題的.
例2 (2017·揚州)如圖3,已知平行四邊形OABC的三個頂點A、B、C在以O為圓心的半圓上,過點C作CD⊥AB,分別交AB、AO的延長線于點D、E,AE交半圓O于點F,連接CF.
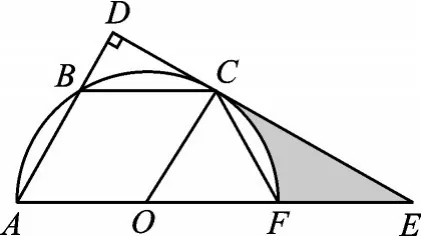
圖3
(1)判斷直線DE與半圓O的位置關系,并說明理由.
【分析】(1)結論:DE是⊙O的切線.由平行四邊形OABC易證∠OCE=90°,即可解決問題?.(?2)①連接 AC,證得∠BCA=∠FAC,得出即CF=AB,可得結論;②只要證明△OCF為等邊三角形即可解決問題.
【解答】(1)DE與半圓O相切.(1分)
理由:∵CD⊥AB,∴∠D=90°.
∵在?ABCO中,∴OC∥AD,
∴∠OCE=∠D=90°,
∴OC⊥DE,又∵OC是半圓O的半徑,
∴DE與半圓O相切.(4分)
(2)①證明:∵在?ABCO中,
連接AC,則∠BCA=∠FAC,∴
∴CF=AB=OC,(7分)
②∵CF=OC=OF,
(2)①求證:CF=OC;②若半圓O的半徑為12,求陰影部分的周長.
【分值猜想】本題滿分10分,共兩大問,3個小問題.在解題過程中,我們為了不丟分,應猜測一下這個10分怎樣分配.在正常情況下結論猜測正確的可以獲得1分,這樣還有9分,剛好分配給3個問題.所以在解題過程中我們就不能遺漏第1問的結論分,即使不會說理,也可以通過猜想得到分數.
【考點】直線與圓的位置關系;平行四邊形的性質;弧長的計算.
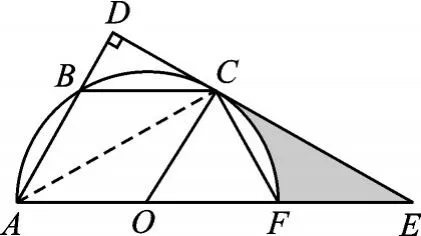
圖4
∴△OCF為等邊三角形,∴∠COF=60°,
∴在Rt△OCE中,
CE=3OC=123,OE=2OC=24,

∴C陰影部分=EF+CE+lC?F=12+124π.(10分)
類型二:12分的壓軸題
這類題目一般都是由3個問題構成,問題難度呈逐漸上升趨勢,入手易,但完整解題較難.
例3 (2017·煙臺)如圖5,菱形ABCD中,對角線 AC,BD 相交于點 O,AC=12cm,BD=16cm,動點N從點D出發,沿線段DB以2cm/s的速度向點B運動,同時動點M從點B出發,沿線段BA以1cm/s的速度向點A運動,當其中一個動點停止運動時另一個動點也隨之停止.設運動時間為t(s)(t>0),以點M為圓心,MB長為半徑的⊙M與射線BA,線段BD分別交于點E,F,連接EN.
(1)求BF的長(用含有t的代數式表示),并求出t的取值范圍.
(2)當t為何值時,線段EN與⊙M相切?
(3)若⊙M與線段EN只有一個公共點,求t的取值范圍.
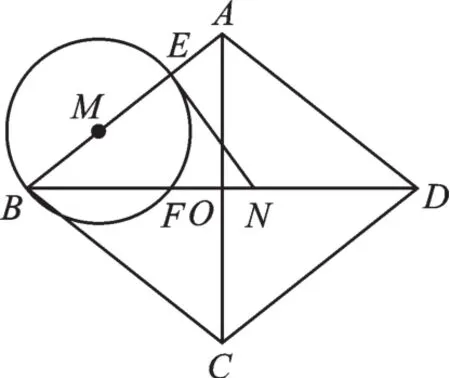
圖5
【分值猜想】本題有3個問題,可猜想每問4分或3分、4分、5分.
【考點】圓的綜合題.
(2)當線段EN與⊙M相切時,易知△BEN∽△BOA,可得解方程即可.
【解答】解:(1)連接MF.
∵四邊形ABCD是菱形,
∴AB=AD,AC⊥BD,OA=OC=6,OB=OD=8,
∵MB=MF,AB=AD,
∴∠ADB=∠ABD=∠MFB,
∴MF∥AD,
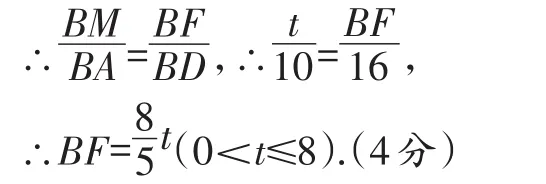
(2)當線段EN與⊙M相切時,易知△BEN∽△BOA,∴
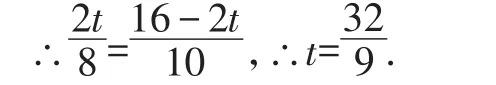
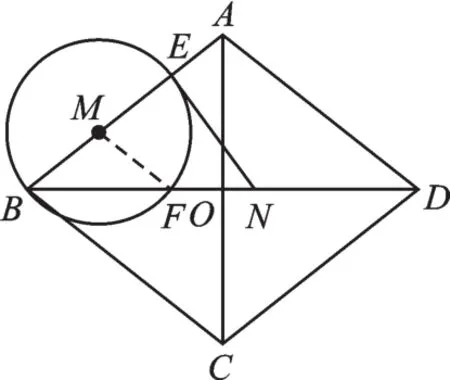
圖6
通過上面的舉例,不難看出,只要我們在平時的練習中,經常分析考點,猜想分值,就會在解題過程中,知道怎樣按考點規范解答,不跳步驟,做一步就能得一分,甚至不會做的也可以從考查方向上解答,盡量多得分,這樣在中考答題中才不會留下遺憾.

