基于離散指數函數優化的GM(1,1)模型在電子裝備系統故障預測中的應用
孫紅影
(三亞學院理工學院,海南 三亞 572022)
1 灰色GM(1,1)模型研究背景
在信息化戰爭理念的指引下,現代化大型艦船電子裝備系統復雜程度也大幅提高。這些武器裝備造價昂貴,試驗維修費用極高。而在實際應用中,影響艦船電子裝備故障因素的種類繁多、實驗數據量較少、具有很大的隨機性與不確定性。因此建立精確模型或者運用大量試驗數據預測故障周期是不現實的。在實際操作過程中只能利用極其有限的試驗數據對系統的故障周期進行預測。灰色GM(1,1)模型是灰色系統預測的基礎與核心。其特點是能用較少的數據序列建立模型去反映系統的主要動態特性。它將系統看成一個隨時間變化而變化的指數函數,因此不需要大量的數據就可以得到很好的預測效果[1-5]。在實際應用中和理論實踐中,人們發現了模型的諸多局限性,對此大家都對模型進行了改進。影響模型精度的原因有很多,但主要原因還是背景值的不足[6]。
本文從背景值出發,將原有的背景值公式進行改進,并將改進的背景值公式的GM(1, 1)模型首次運用到艦船的電子裝備系統的故障預測中。通過數據模擬和模型比較表明,與傳統的GM(1,1)模型相比,本文改進的模型的預測精度有顯著提高,能使其更好地服務于艦船電子裝備系統,有十分重要的意義。
2 GM(1,1)模型背景值最優化
2.1 GM(1,1)模型及誤差原因
的一次累加生成序列
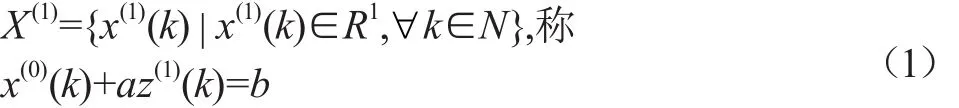
為GM(1,1)模型的定義式,也稱為灰色微分方程。這里

式(2)中的z(1)(k)稱為GM(1,1)模型的背景值,為累加生成序列的緊鄰均值生成值。
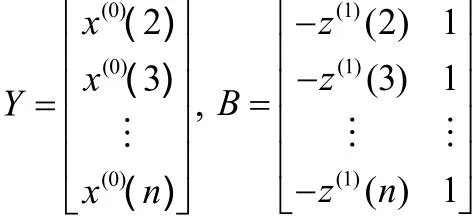
則GM(1,1)模型參數的最小二乘估計為

定義GM(1,1)模型的白化微分方程為

則灰色微分方程x(0)(k)+az(1)(k)=b的時間響應式為
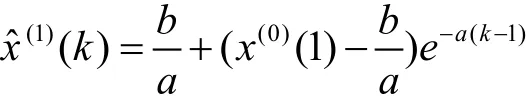
其中,k=1,2,…,n
累減還原值為

由此可見,傳統的背景值計算公式實質上是用梯形公式近似的計算x(1)(t)在區間[k-1,k]上與t軸圍成的面積。公式(2)是一個平滑公式,當時間間隔很小,序列數據變化平緩時,這樣構造的背景值是合適的。模型偏差較小,但當序列數據變化急劇時,這樣構造出來的背景值往往產生較大的滯后誤差,模型偏差較大。
2.2 背景值的優化
在區間[k-1,k]上對白化方程兩邊求積分


將式(6)代入z(1)(k)得
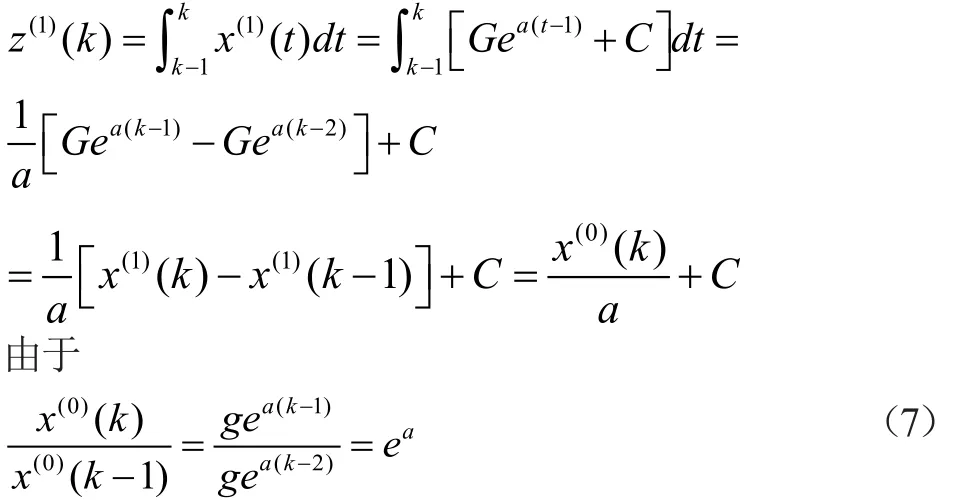
所以
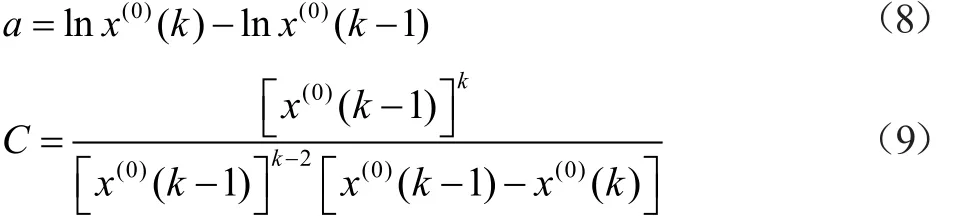
將a和C的表達式代入z(1)(k)得到新構造的背景值計算公式

2.3 利用最優化的背景值建模
灰色微分方程x(0)(k)+az(1)(k)=b的最小二乘估計參數序列為
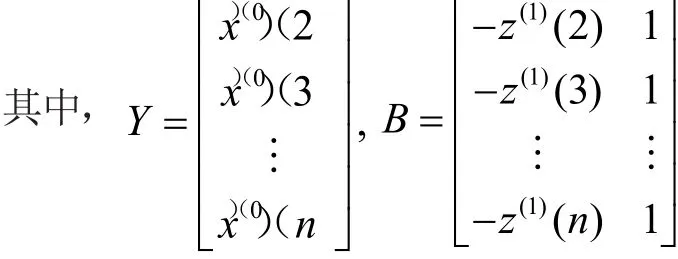
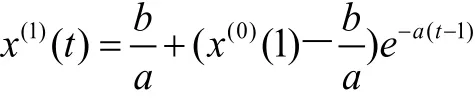
(2)灰色微分方程x(0)(k)+az(1)(k)=b的時間響應式為:
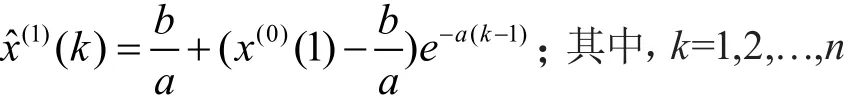
(3)還原值
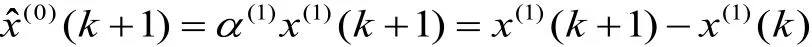
3 GM(1.1)模型在電子設備故障預測中的應用
根據文獻[7]中某電子裝備在高溫季節的失效數據,如表1所示,選取10個連續數據作為樣本。其中k表示第k次失效,t表示失效時刻。

表1 雷達累積失效時刻
運用已知的數據,運用上面優化的方法,對該裝備試驗過程中某次故障發生時,其失效時間進行估計。通過Matlab編程仿真,可以得到如表2所示結果。
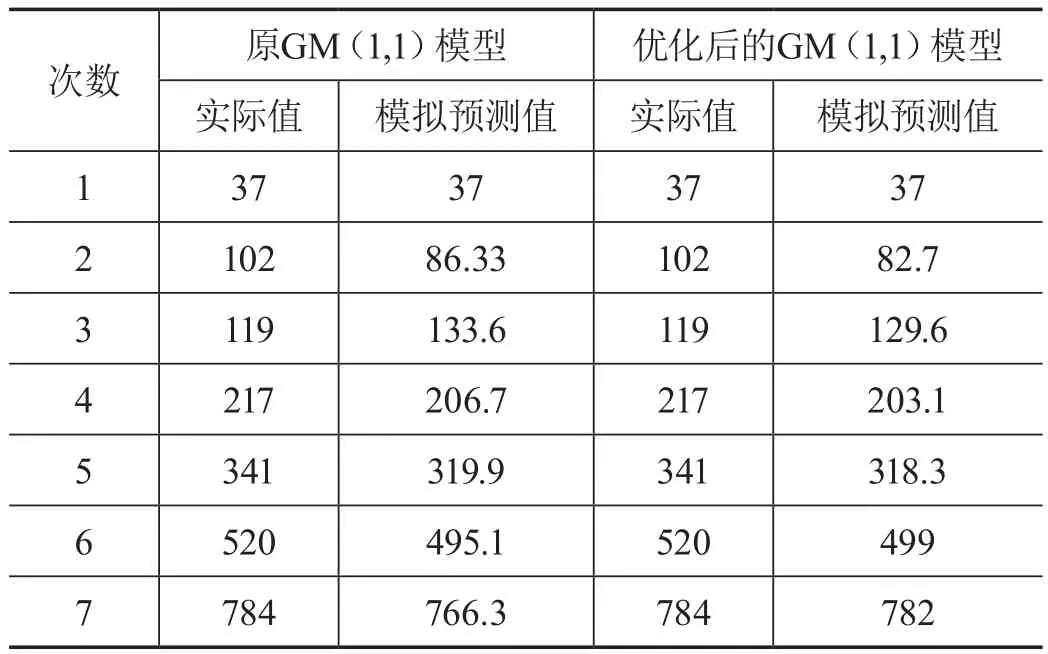
表2 兩種模型的模擬預測值與實際值得比較
其中,1—5次為模擬值,6—7次為預測值。
進一步計算兩種模型的模擬誤差與預測誤差,如表3—4所示。

表3 兩種模型對故障失效時間的模擬誤差(%)

表4 兩種模型對故障失效時間的預測相對誤差(%)
由表3可以看出來,優化之后的模型的誤差要顯著地小于原GM(1,1)模型,這說明優化后的模型精度要高于原模型,這個也是模型具有較高的預測精度的前提條件:由表4可以看出,優化后的模型對第六次和第七次故障失效時間的預測相對誤差為4.04%和0.26%,都小于原GM(1,1)模型。特別是第七次的預測精度達到了0.26%,從而可以看出來優化后的模型在模擬、預測方面具有的優勢。
4 結語
本文通過對某電子裝備在高溫季節的失效數據的分析,針對數據是離散的且累加后為指數函數的特性,在傳統的灰色GM(1,1)模型的基礎上從背景值入手進行模型改進。通過仿真實驗,將改進后的模型與傳統的GM(1,1)模型的模擬精度與預測精度進行對比,得出優化后的模型的精度要高于傳統的GM(1,1)模型,證明了新模型的可行性,即可提高艦船的電子系統的故障預測精度,能為裝備平時的維修保養提供數據支撐,對研究武器裝備的可靠性具有重大的現實意義。本文對模型的參量的選取有一定的局限性,且依賴于原始數據,對此可以進行進一步的研究。
[參考文獻]
[1]鄧聚龍.灰預測與決策(修訂版)[M].武漢:華中科技大學出版社,2002.
[2]劉思峰,黨耀國,方志耕. 灰色系統理論及其應用[M].3版.北京:科學出版社,2004.
[3]LIU S F,FORREST J.The role and position of grey system theory in science development[J].Grey System (UK),1997(4):351-356.
[4]肖新平,宋中民,李峰.灰技術基礎及其應用[M].北京:科學出版社,2005.
[5]張岐山.灰朦朧集的差異性信息理論[M].北京:石油工業出版社,2002.
[6]譚冠軍.GM(1,1)模型的背景值構造方法和應用(I)[J].系統工程理論與實踐,2000(5):98-103.
[7]賈占強,梁玉英.灰色GM(1,1)模型在電子裝備壽命預測中的應用[J].火力與指揮控制,2008(11):134-143.

