長引水大流量水電站小波動調節保證設計仿真計算
李明橋,余 洋,劉 君,劉建華,雷 亮
(1.中國電建集團西北勘測設計研究院有限公司,西安 710065;2.高縣水務局,四川省宜賓市 645150)
0 前 言
小波動過渡過程是指水力-機械系統中出現小波動時,在調速器和其他控制裝置的作用下,系統恢復到初始穩定運行狀態或達到新的穩定狀態并長時間保持穩定運行的能力。小波動運行是否穩定取決于系統自身特性,與所受干擾無關,系統自身特性主要包括水道特性、運行工況點特性、調速器特性、運行方式及負荷特性等。對于設置調壓室的水電站而言,調壓室穩定面積的確定是小波動穩定性分析的重要內容。通常,調壓室的穩定面積是以托馬斷面為極限最小面積,而托馬斷面是以孤立電站小波動穩定性確定的調壓室斷面面積,安全系數較大。隨著電力系統容量的增大和電器裝置的完善,國內外一些電站在設計中考慮系統或調速器的作用等因素,采用了小于托馬條件的調壓室穩定斷面的面積,有些電站的調壓室面積已達到托馬斷面的40%左右[1]。因此,在進行大波動過渡過程計算分析的同時,進行不同調壓室面積的小波動過渡過程分析,對于滿足系統穩定性和提高調節品質,優化調壓室穩定斷面面積,降低工程造價具有積極意義。
隨著中國水電事業的快速發展,有些水電站由于受地形條件的限制不得不修建超長的引水隧洞,這類電站的引水隧洞長度一般都達到了5 km有些甚至超過了15 km,該類型水電站由于引水隧洞太長,水流慣性極大[2],小波動過渡過程穩定性問題突出。本文以四川某水電站為例,引水隧洞長度約8 km,引用流量242 m3/s,屬于典型的長引水、大流量水電站工程。結合工程特點,擬定不同的調壓室斷面尺寸和調速器參數,運用數字仿真計算方法,最終找出滿足穩定運行保證調節品質的最優調壓室斷面和調速器參數整定值。
1 仿真計算基本理論及方法
小波動穩定計算和分析主要采用2種方法,一種是基于狀態方程的剛性水錘分析方法,另外一種是基于特征線法考慮水體彈性的分析方法[3]。本文采用剛性水錘模型,并假定負荷擾動及上、下游水位擾動均是微小量,因而可略去系統基本方程式中的高階微分項(即線性化處理)。
(1) 水流動力方程
(1)
(2)
(3)
(4)
(5)
(6)
式中:Hu為水電站上庫水位;Htui、Htdi(i=1~2)為機組進、出口壓力水頭;Zu為上游調壓室水位;Li、Ai分別為第i段管道長度、面積(i=1~31);QT為進水口至上游調壓室管段流量;Q0為調壓室至分岔管段流量;Q1為1號機組引用流量;Q2為2號機組引用流量;HB為上游分岔點測壓管水頭;HT為電站下庫水位;g為重力加速度。
(2) 水流連續方程
(7)
式中:QT為進水口至上游調壓室管段流量;Q0為調壓室至分岔管段流量;Fu為上游調壓室斷面積;Zu為上游調壓室水位變化量。
(3) 管道水流控制方程線性化處理
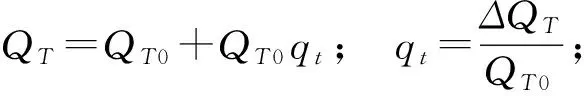
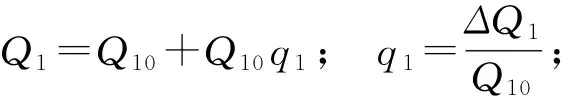

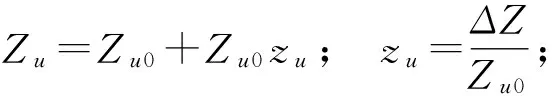
Htu1=Htu10+ΔH11;Htd1=Htd10+ΔH21;
Htu2=Htu20+ΔH12;Htd2=Htd20+ΔH22;
(4) 調速器方程
設D1i、Q1i′、PTi、ηi、n1i′、ni、τi(i=1~2)分別表示各水輪機的直徑、單位流量、出力、效率、單位轉速、轉速及導葉開度,則水輪機的出流、轉速、出力方程為:
(8)
(9)
(10)
式中:Q1i′=Q1i′(n1i′,τi)、M1i′=M1i′(n1i′,τi)為反映本電站機組特性的流量與力矩綜合特性曲線[4]。
2 仿真計算
2.1 水電站基本資料
四川某水電站為引水式電站,引水發電系統由擋水閘壩、有壓引水隧洞、調壓室和地面廠房組成,引水洞直徑 9.4 m,引水線路全長約8 km,水電站裝機 2臺46 MW混流式水輪機組,額定水頭43 m,引用流量 243 m3/s,上游正常蓄水位789.00 m,下游死水位784.00 m。采用“1洞2機”布置,上游設置阻抗式調壓室。從水電站基本參數可以看出,工程算例屬于較為典型的長引水、大流量、低水頭水電站工程,壓力水道水流慣性時間常數Tw較大,調壓室托馬臨界穩定斷面面積理論計算值F遠大于比選方案調壓室斷面面積。本文擬定了不同調壓室尺寸和調速器參數的組合方案,分別在控制工況下進行小波動分析計算,對引水發電系統進行當量化處理,水電站水道系統布置如圖1所示,仿真計算模型如圖2所示。
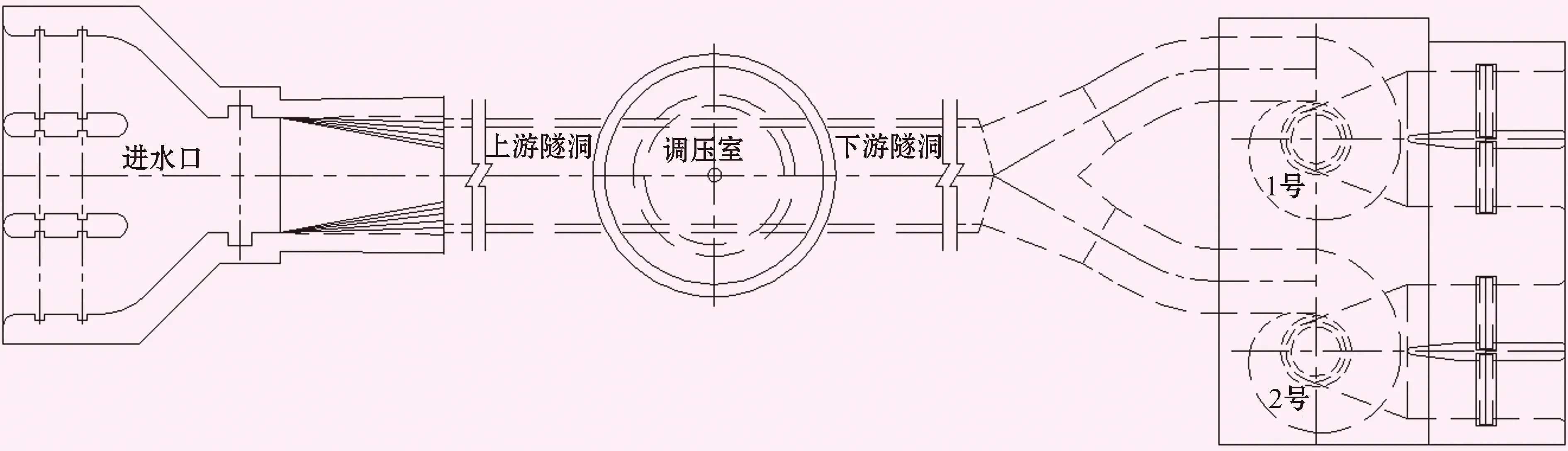
圖1 水電站水道系統布置簡圖
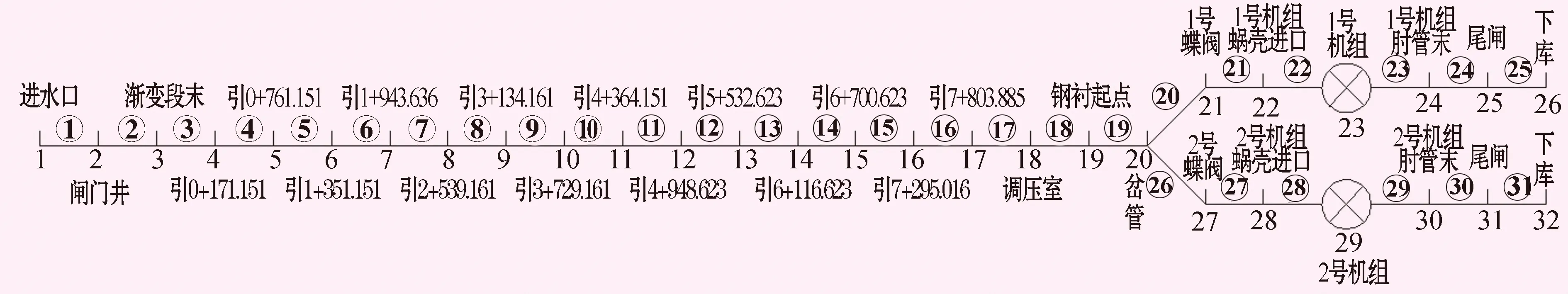
圖2 仿真計算模型圖 單位:m
2.2 控制工況
水電站小波動穩定性與水輪機的水頭損失系數、工作水頭有關,水頭損失系數越小、工作水頭越小,穩定性越差。同時考慮水輪機機組及調速器特性,系統小波動穩定性也與機組穩定運行工況點特性參數和調速器整定參數有關。為研究調壓室穩定斷面、機組調節品質,初步擬定控制工況如表1所示。

表1 小波動過渡過程仿真計算工況表
2.3 小波動仿真計算
調速器參數在常規范圍內取值時微分時間常數Tn取值范圍在0~2 s之間,暫態轉差系數Bt取值范圍在1%~200%之,Td取值范圍在0~20 s之間。
方案1:調壓室大井直徑取32 m,阻抗孔口直徑取5 m,電站負荷自調節系數Ep分別取1.8和2.0。圖3、4分別為調壓室大井直徑D=32 m、Ep=1.8和大井直徑D=32 m、Ep=2.0時,小波動仿真計算得到的穩定域,計算時微分時間常數Tn=1.5,永態轉差系數Bp=0。
方案1計算結果: 調壓室大井直徑D=32 m,系統負荷自調節系數Ep=1.8的情況下,基本能保證電站小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95時,能滿足穩定品質要求;若調速器參數減小,將不能滿足穩定品質要求。調壓室大井直徑D=32 m,系統負荷自調節系數Ep=2.0的情況下,基本能保證小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95時,能滿足穩定品質要求;若調速器參數減小,將不滿足穩定品質要求。

圖3 方案1:Ep=1.8時的不同工況小波動穩定域圖

圖4 方案1:Ep=2.0時的不同工況小波動穩定域圖
方案2:調壓室大井直徑取34 m,阻抗孔口直徑取5 m,電站負荷自調節系數Ep分別取1.8和2.0。圖5、6分別為調壓室大井直徑D=34 m、Ep=1.8和大井直徑D=34 m、Ep=2.0時,小波動仿真計算得到的穩定域,計算時微分時間常數Tn=1.5,永態轉差系數Bp=0。
方案2計算結果: 調壓室大井直徑D=34 m,系統負荷自調節系數Ep=1.8的情況下,基本能保證電站小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95時,能滿足穩定品質要求。若調速器參數減小,將不能滿足穩定品質要求。調壓室大井直徑D=34 m,系統負荷自調節系數Ep=2.0的情況下,基本能保證小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95;Td=18.0、Bt=1.90時,均能滿足穩定品質要求,該情況下,調速器參數取值具有一定的裕量。

圖5 方案2:Ep=1.8時的不同工況小波動穩定域圖

圖6 方案2:Ep=2.0時的不同工況小波動穩定域圖
方案3:調壓室大井直徑取36 m,阻抗孔口直徑取5 m,電站負荷自調節系數Ep分別取1.8和2.0。圖7和圖8分別為調壓室大井直徑D=36 m、Ep=1.8,大井直徑D=36 m、Ep=2.0時,小波動仿真計算得到的穩定域,計算時微分時間常數Tn=1.5,永態轉差系數Bp=0。
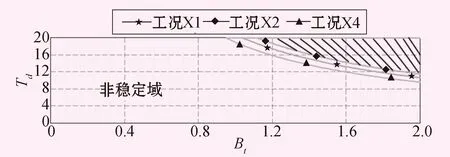
圖7 方案3:Ep=1.8時的不同工況小波動穩定域圖
方案3計算結果: 調壓室大井直徑D=36 m,系統負荷自調節系數Ep=1.8的情況下,基本能保證電站小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95;Td=18.0、Bt=1.90時,均能滿足穩定品質要求;該情況下,調速器參數取值具有一定的裕量。調壓室大井直徑D=36 m,系統負荷自調節系數Ep=2.0的情況下,基本能保證小波動穩定運行,調速器參數取值Td=19.8、Bt=1.95,Td=18.0、Bt=1.90,Td=17.0、Bt=1.80時,均能滿足穩定品質要求;該情況下,調速器參數整定值的魯棒性較好。
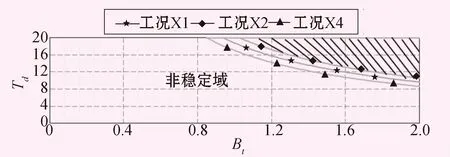
圖8 方案3:Ep=2.0時的不同工況小波動穩定域圖
3 結 語
該水電站引水隧洞長、流量大,水頭較低,引水發電系統Tw值較大,機組特性對系統的穩定性較為不利,小波動穩定性問題尤為突出。分析計算結果可知,對于X1、X2和X4三個控制工況,當調壓室大井直徑一定,電站系統負荷自調節系數Ep取1.8和2.0時,系統小波動均存在穩定域,圖中陰影部分為3個控制工況共有的穩定域面積,且Ep值越大,穩定域面積越大,調速器參數在共同穩定域內取值,可滿足水電站小波動穩定運行;對于整個引水發電系統來說,調壓室斷面尺寸對小波動穩定性影響更大,其敏感性遠大于系統負荷自調節系數,當系統負荷自調節系數一定時,調壓室斷面面積越大,水電站小波動運行穩定性越好,穩定域越大,調節品質越好[5]。
調壓室大井直徑D=34 m,系統負荷自調節系數Ep=2.0;調壓室大井直徑D=36 m,系統負荷自調節系數Ep=1.8兩種組合,基本能保證本電站小波動穩定運行,且調速器參數有一定裕量。
調壓室大井直徑D=36 m,系統負荷自調節系數Ep=2.0時,能夠保證電站小波動穩定運行,且調速器參數裕量最大,調節品質相對最好。工程實際中,綜合電站建設工程造價、建設工期考慮,建議調壓室直徑不小于34 m。
參考文獻:
[1] 鄭源.張健.水力機組過渡過程[M].北京:北京大學出版社出版時間,2008.
[2] 付亮,楊建東,王建偉.超長引水隧洞水電站大波動過渡過程特殊問題[J].中國農村水利水電,2006(09): 112-114.
[3] 周建旭,鄭源.水電站小波動穩定性分析方法的研究[J].江西水利科技,2004(03):125-128.
[4] 朱寧.自動控制理論[M].北京:清華大學出版社,2014.
[5] 方杰,汪德樓,陳順義.錦屏二級水電站小波動穩定性分析及對策研究[J].人民長江,2016(19): 111-114.

