空天飛行器彈道/軌道一體化設(shè)計

方群，劉怡思，王雪峰

1.西北工業(yè)大學 航天學院，西安 710072 2.西北工業(yè)大學 航天飛行動力學技術(shù)國家重點實驗室，西安 710072

空天飛行器是航空航天飛行器的簡稱，是航空技術(shù)與航天技術(shù)高度結(jié)合的飛行器。在現(xiàn)代空天飛行器的飛行任務(wù)中，越來越多地涉及到了大氣層內(nèi)外的穿梭，因此彈道/軌道一體化設(shè)計的需求也越來越凸顯[1]。彈道/軌道一體化設(shè)計具有精度高、易于優(yōu)化的優(yōu)點，同時也能從宏觀角度整體、全面地描述和設(shè)計空天飛行器的整個任務(wù)軌跡[2]。目前，針對彈道/軌道一體化設(shè)計的研究主要是集中在任務(wù)一體化和參數(shù)一體化上：任務(wù)一體化的設(shè)計方法是根據(jù)飛行器的飛行任務(wù)將飛行軌跡分為彈道段和軌道段分別建模設(shè)計，然后將設(shè)計結(jié)果按照任務(wù)要求進行拼接，最終得到完整的彈道/軌道設(shè)計結(jié)果；而參數(shù)一體化的設(shè)計方法是將軌道六要素用彈道的相關(guān)參數(shù)來表示，從而統(tǒng)一整個彈道段和軌道段參數(shù)，將彈道和軌道的設(shè)計轉(zhuǎn)化為彈道參數(shù)的設(shè)計[2-5]。上述方法存在的主要問題是沒有建立統(tǒng)一的空天飛行器動力學模型，因此不能真實準確地描述空天飛行器的受力和運動情況。同時彈道方程較為復(fù)雜，參數(shù)數(shù)量多，不易于優(yōu)化。

由于彈道是飛行器在大氣層內(nèi)飛行時質(zhì)心的運動軌跡，而軌道則是飛行器運動在外層空間中質(zhì)心的運動軌跡，因此兩者雖然都是表征飛行器運動軌跡的特征曲線，但有著區(qū)別較大的飛行環(huán)境，以及不同的動力學特性。為此針對大氣層內(nèi)和大氣層外力學環(huán)境不同難以統(tǒng)一動力學建模的問題，羅亞中等采用將軌跡拆分再拼接的建模方法[4-6]，將整個任務(wù)軌跡拆分為彈道段和軌道段來分別求解，最后將所得結(jié)果拼接獲得整個空天飛行器的軌跡解。該方法的特點是利用拆分再拼接的方法將任務(wù)軌跡拆分為彈道段和軌道段，使得原本變量耦合的復(fù)雜問題變成了采用兩種算法以一定的時間順序分別求解兩個相對簡單的問題，所建立的算法和模型具有較廣泛的適應(yīng)性。但是由于這種簡單的拆分拼接所反映的是一種單一任務(wù)過程，針對多次重復(fù)往返大氣層的任務(wù)該方法將難以反映真實情況，同時這種建模方法在彈道和軌道的轉(zhuǎn)換段精度較低，并且由于這種方法要進行彈道和軌道的聯(lián)合設(shè)計，所以如果有一方設(shè)計結(jié)果不理想，將會影響到另一方的設(shè)計結(jié)果和精度。另外這種分段設(shè)計再拼接的方法也難以進行軌道的優(yōu)化設(shè)計。

針對上述方法優(yōu)化難以進行的問題，張衛(wèi)華等提出了一種彈/軌參數(shù)一體化建模和優(yōu)化方法[3,7]。該方法利用彈道參數(shù)和軌道參數(shù)之間的轉(zhuǎn)化關(guān)系來統(tǒng)一處理任務(wù)軌跡，利用彈道參數(shù)來表示軌道根數(shù)，從而實現(xiàn)了將整個過程轉(zhuǎn)化為對彈道發(fā)射參數(shù)以及控制的優(yōu)化。該方法實現(xiàn)了彈道/軌道的參數(shù)一體化，從而使得對任務(wù)軌跡的整體優(yōu)化問題轉(zhuǎn)化為對發(fā)射初始參數(shù)和控制律的優(yōu)化問題，得到了滿足任務(wù)需求的優(yōu)化結(jié)果。然而，這種方法依然沒有擺脫將任務(wù)軌跡分解為彈道和軌道簡單疊加的建模方法，將一個實際上存在較強耦合的問題人為地線性化，一個實際上較為復(fù)雜的任務(wù)進程順序化、簡單化，從而導(dǎo)致無論是建模的精度還是優(yōu)化的程度都存在著明顯的不足。

由此可見，目前針對空天飛行器軌道設(shè)計所采用的方法主要是將飛行器的任務(wù)軌跡拆分為彈道段和軌道段，對彈道段和軌道段分別進行設(shè)計，再拼接產(chǎn)生空天飛行器軌道設(shè)計結(jié)果。這種方法計算效率較低，并且不利于后續(xù)的優(yōu)化設(shè)計。為此亟待解決針對空天飛行器的彈道/軌道一體化建模以及整體優(yōu)化設(shè)計的問題。本文首先提出采用軌道方程統(tǒng)一描述空天飛行器彈道/軌道一體化建模思想，即將除引力之外的合力都視為攝動力，并寫入軌道攝動方程中，從而建立彈道/軌道一體化動力學模型。然后在此基礎(chǔ)上，提出基于軌道設(shè)計反方法的彈道/軌道一體化設(shè)計方法。仿真分析表明本文提出的彈道/軌道一體化設(shè)計方法是可行和有效的，為空天飛行器的軌道設(shè)計開辟了新的思路。

1 彈道/軌道一體化設(shè)計

1.1 極坐標下的飛行器動力學建模

假設(shè)飛行器處于二體引力場中，即飛行器只受中心天體地球引力的影響，且中心天體地球?qū)︼w行器的引力為指向地心，引力大小與飛行器到地心距離的平方成反比，飛行器所受的其他力全部作為攝動力來表述。建立以地心為極點，從地心出發(fā)沿著赤道向某方向的射線作為極軸的二維極坐標下的軌道攝動方程為

(1)

式中：r為飛行器的位置矢量，r=‖r‖為飛行器位置矢量的模，表示飛行器到坐標原點即地心的距離；m為飛行器的質(zhì)量；f表示除了引力之外飛行器所受的其他力的合力；μ為引力常數(shù)。

圖1為極坐標下的飛行器受力圖，O表示中心天體，A表示飛行器的質(zhì)心，極角θ和距離r為兩個自變量，表征飛行器的位置，V為飛行器的速度。令R為飛行器徑向單位矢量，θ為法向單位矢量，γ為V與θ的夾角。

由r=rR，有

(2)

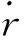
(3)

圖1 極坐標下的飛行器受力Fig.1 Forces of aircraft in polar coordinate

將式(3)代入式(1)，有

(4)

將式(4)沿徑向和法向展開，有[8-11]

(5)

式中：fjing和ffa分別為除引力外其他作用力在徑向和法向的投影。

飛行器除引力之外的其他受力如圖2所示。圖中：A點表示飛行器的質(zhì)心，兩條虛線表示θ和R的單位矢量方向，L是飛行器所受的升力，D是飛行器所受的空氣阻力，F(xiàn)為飛行器的推力，假設(shè)發(fā)動機沒有安裝偏差角，則迎角α即為推力方向與V之間的夾角。

將除引力之外的氣動力和推力代入式(5)，有

(6)

根據(jù)γ的定義，有

(7)

而位置矢量的極坐標形式為r=(rcosθ,rsinθ)，則有

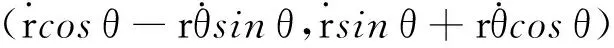
(8)

將式(8)代入式(7)，可得

(9)

圖2 飛行器所受除引力之外的其他力Fig.2 Forces of aircraft except gravity

將式(9)代入式(6)，有

(10)

定義無量綱化地心距、時間、速度以及各力分別為

(11)

(12)

(13)

(14)

式中：r0為地球半徑；v為飛行器速率。經(jīng)無量綱處理后，式(10)可表示為

(15)

式中：z′、z″、θ′和θ″分別為各個變量對廣義時間τ的一、二階導(dǎo)數(shù)。

由式(12)，有

(16)

由此可得

(17)

將式(16)、式(17)代入式(15)，得極坐標下飛行器無量綱動力學模型為

(18)

1.2 無量綱處理

為了編程方便，將式(18)寫成便于積分的形式，即

(19)

為了實現(xiàn)彈道/軌道的一體化設(shè)計，需要將動力學模型式(19)轉(zhuǎn)化為只含有狀態(tài)變量z、z′、θ、θ′和時間τ以及控制變量f、α的方程組，其他參數(shù)包括m、l和d等需要用狀態(tài)變量、控制變量與飛行器的特性參數(shù)來表示，其具體過程如下所述。

1) 氣動力

升力、阻力的基本計算模型為

(20)

(21)

式中：CL為升力系數(shù)；CD為阻力系數(shù)；ρ為大氣密度；s為飛行器橫截面積。

選取某型號飛行器為研究對象，對該飛行器在雷諾數(shù)Re=1.34，馬赫數(shù)Ma=8.02，努森數(shù)Kn=0.001下的氣動力系數(shù)進行了仿真計算，其結(jié)果如表1所示。

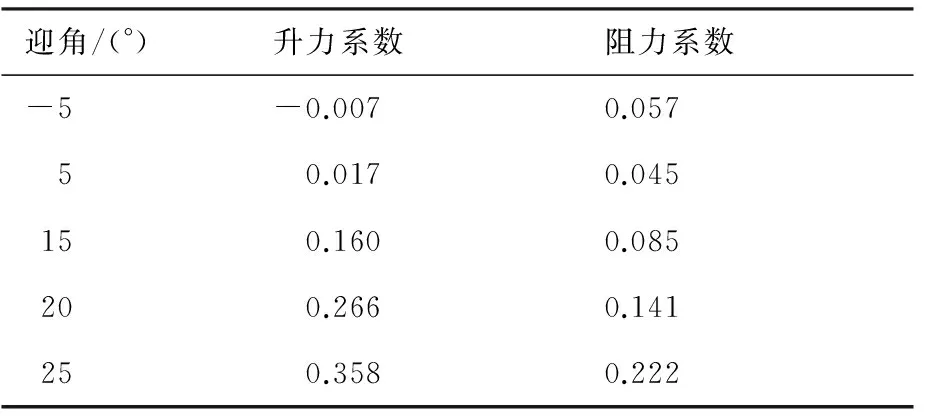
表1 某飛行器的氣動參數(shù)計算結(jié)果

經(jīng)擬合之后得到升力系數(shù)CL及阻力系數(shù)CD的表達式為

CL=1.253 4(α-γ)2+

0.259 6(α-γ)+0.006 1

(22)

CD=1.346 2(α-γ)2-

0.154 7(α-γ)+0.033 2

(23)

2) 飛行速率

飛行速率的無量綱表達式為

(24)

將式(17)代入式(24)，得飛行速率的無量綱表達式為

3) 推 力

由于本文推力是作為設(shè)計量和優(yōu)化量來處理的，因此推力可以看作可控制力，為此只需要給出推力約束條件即可，即

{F∈[0,Fmax]

Is=uef

(25)

式中：Fmax為最大推力；Is為發(fā)動機的比沖；uef為等效噴氣速度。

4) 飛行器質(zhì)量

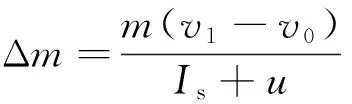
(26)

式中：v0、v1分別為飛行器初速率和末速率。

將式(12)代入式(26)，則有

(27)

式中：v為無量綱化之前的飛行器速度，由式(24)確定，由此可得

(28)

式中：v′為飛行速度對廣義時間的導(dǎo)數(shù)。

5) 無量綱的一體化模型

將式(20)～式(28)整理之后,得到式(19)可積分的形式為

圖4 彈道設(shè)計仿真結(jié)果Fig.4 Simulation results of trajectory design

3.2 軌道設(shè)計

將3.1節(jié)彈道設(shè)計的結(jié)果作為初值，目標軌道設(shè)定為軌道高度為35 860 km的圓軌道，即地球同步軌道。取距離單位為1 DU=1Rearth，Rearth為地球半徑,時間單位為1 TU=806.8 s，推力約束為Fmax=0.01 DU/TU2。得到仿真結(jié)果如圖5和圖6所示，圖5為應(yīng)用形狀方法得到的飛行器軌跡，圖6為飛行器推力加速度ac隨時間t變化的曲線。

由于本節(jié)的設(shè)計是將3.1節(jié)設(shè)計結(jié)果的末狀態(tài)作為初值，所以其與3.1節(jié)的彈道設(shè)計結(jié)果能夠自然地銜接，如此就完成了整個彈道/軌道的一體化設(shè)計。

圖5 形狀軌道Fig.5 Shape-based trajectory

圖6 飛行器軌道機動所需的推力加速度Fig.6 Required thrust acceleration using aircraft orbit maneuver

4 結(jié) 論

1) 提出了采用軌道方程統(tǒng)一描述彈道/軌道的思想，即將除引力之外的合力都視為攝動力，并寫入軌道攝動方程的攝動力項中，通過整合連續(xù)推力、氣動力、引力以及攝動力等多種作用力，建立彈道/軌道一體化動力學模型，為空天飛行器一體化軌道設(shè)計建立基礎(chǔ)。

2) 為了解決目前存在的彈道段軌跡設(shè)計方法與軌道段軌跡設(shè)計方法不統(tǒng)一的問題，將軌道設(shè)計中的反方法設(shè)計思想應(yīng)用于彈道設(shè)計中，提出了一種基于彈道/軌道一體化模型的彈道設(shè)計反方法，使得同時從模型與方法的角度體現(xiàn)一體化的設(shè)計思想。

3) 將彈道段的終端狀態(tài)參數(shù)值作為初值，目標軌道參數(shù)值作為終值，通過合理選擇軌道轉(zhuǎn)移時間和繞轉(zhuǎn)圈數(shù)，采用基于傅里葉級數(shù)展開的形狀方法，完成了軌道段軌跡的設(shè)計。由于是將彈道段的末狀態(tài)作為軌道段的初值，所以軌道設(shè)計結(jié)果能夠自然地與彈道銜接，形成了整個彈道/軌道的一體化設(shè)計結(jié)果。

4) 本文提出的彈道/軌道一體化設(shè)計方法的適用性和限制條件為：① 由于針對三維空間的軌跡設(shè)計需要考慮姿態(tài)運動方程，目前還不能實現(xiàn)統(tǒng)一建模，故現(xiàn)階段該方法只能應(yīng)用于二維平面的軌跡設(shè)計；② 應(yīng)用傅里葉級數(shù)法設(shè)計軌道段，需要事先給出一個飛行時間。與此同時，考慮到傅里葉級數(shù)的項數(shù)對計算效率和精度的影響，項數(shù)不能無限增加。

雖然目前本文方法受技術(shù)瓶頸的制約還存在著應(yīng)用局限性，但給未來先進空天飛行器的彈道/軌道一體化設(shè)計提出了新的思路和技術(shù)途徑。隨著相關(guān)技術(shù)問題的解決，方法的適用性將會得到提高。

[1] 趙瑞安.空間武器軌道設(shè)計[M]. 北京: 中國宇航出版社, 2008: 176-178.

ZHAO R A. Space weapon orbit design[M]. Beijing: China Astronautic Press, 2008: 176-178 (in Chinese).

[2] 黃文博, 張強, 肖飛，等. 空間快速響應(yīng)航天器軌道/彈道一體化規(guī)劃[J]. 固體火箭技術(shù), 2012, 35(1): 11-16.

HANG W B, ZHANG Q, XIAO F, et al.Orbit-trajectory integrated programming for operationally responsive space spacecraft[J]. Journal of Solid Rocket Technology, 2013, 35(1): 11-16 (in Chinese).

[3] 肖飛, 向敏, 張衛(wèi)華. 多級運載火箭總體/彈道/軌道一體化設(shè)計與優(yōu)化[J]. 空軍工程大學學報， 2008, 9(5): 19-23.

XIAO F, XIANG M, ZHANG W H. Orbit trajectory and system integration design and optimization of multi-stage solid rocket[J]. Journal of Airforce Engineering University, 2008, 9(5): 19-23 (in Chinese).

[4] 羅亞中, 唐國金, 梁彥剛, 等.近地軌道運載火箭軌跡/總體參數(shù)一體化設(shè)計與優(yōu)化[J]. 中國空間科學技術(shù)， 2003，10(5)： 16-32.

LUO Y Z, TANG G J, LIANG Y G, et al. Integrated optimization design for trajectory/system parameter of low earth orbit launch vehicle[J]. Chinese Space Science and Technology, 2003, 10(5): 16-32 (in Chinese).

[5] 羅亞中, 唐國金, 梁彥剛. 基于分解策略的SSO發(fā)射軌道遺傳全局優(yōu)化設(shè)計[J]. 航空學報， 2004， 25(5)： 443-446.

LUO Y Z, TANG G J, LIANG Y G. Decomposition approach and genetic algorithm based global optimization of launch trajectory for sun synchronous orbit[J]. Acta Aeronautica et Astronautica Sinica, 2004， 25(5)： 443-446 (in Chinese).

[6] 羅亞中, 唐國金, 梁彥剛, 等. GTO發(fā)射軌道的兩級分解全局優(yōu)化設(shè)計策略[J]. 中國空間科學技術(shù)， 2004, 24(4)： 36-46.

LUO Y Z, TANG G J, LIANG Y G, et al. Bilevel decomposition based global optimization approach for launch trajectory of GTO launchers[J]. Chinese Space Science and Technology, 2004,24(4): 36-46 (in Chinese).

[7] 楊希祥, 江振宇, 張衛(wèi)華. 小型運載火箭大氣層飛行段飛行程序設(shè)計研究[J]. 飛行力學, 2010, 28(4): 68-72.

YANG X X, JIANG Z Y, ZHANG W H. Flight program design for small launch vehicle in atmosphere flight stage[J]. Flight Dynamics, 2010, 28(4): 68-72 (in Chinese).

[8] BATTIN R H. An introduction to the mathematics and method of astrodynamics[M]. New York: AIAA Education Series, 1987: 408-418.

[9] BATTIN R H, FILL T J. Extension of gauss method for the solution of Kepler’s equation[J]. Journal of Guidance, Control and Dynamics, 1979, 2(5-6): 190-195.

[10] BATTIN R H.A scrapbook of beautiful equations and great ideas[C]∥ Astrodynamics Symposium, 2000:423-433.

[11] 鄭莉莉. 連續(xù)推力作用下的機動軌道設(shè)計與優(yōu)化[D]. 西安: 西北工業(yè)大學, 2011: 15-43.

ZHENG L L. Orbit design and optimization for spacecraft maneuver under continuous thrust[D]. Xi’an: Northwestern Polytechnical University, 2011: 15-43 (in Chinese).

[12] TAHERI E, ABDELKHALIK O. Shaped-based approximation of constrained low-thrust space trajectory using Fourier series[J]. Journal of Spacecraft and Rockets, 2012, 49(3): 535-546.