一種基于軌道根數(shù)約束的最優(yōu)制導(dǎo)方法

李超兵，呂春紅，尚騰

北京航天自動控制研究所，北京 100854

在空間航天器為完成預(yù)定任務(wù)，需要通過變軌控制來實現(xiàn)不同軌道之間的轉(zhuǎn)移，而為確保航天器能夠到達目標(biāo)軌道，同時節(jié)省變軌控制的燃料消耗，需要利用最優(yōu)控制原理設(shè)計制導(dǎo)算法。

以迭代制導(dǎo)為代表的最優(yōu)制導(dǎo)算法自應(yīng)用于美國的土星五號運載器以來，逐漸為許多航天器所采納[1-3]。針對航天器主發(fā)動機推力大小不可調(diào)的情況，傳統(tǒng)迭代制導(dǎo)通常以2個方向的位置和3個方向的速度作為5個終端約束，假設(shè)控制角指令由速度約束和位置約束兩部分組成，并且位置約束部分為小量[4-7]，這樣可以首先求解滿足速度約束部分的控制角，然后利用小角度近似求解滿足位置約束部分的控制角。但這一假設(shè)并無嚴格的理論支撐，且在某些變軌情形下這一假設(shè)不再成立，從而限制了傳統(tǒng)迭代制導(dǎo)的進一步應(yīng)用[8-11]。

針對傳統(tǒng)迭代制導(dǎo)的不足，研究人員從不同的角度進行了改進研究。陳新民和余夢倫[12]針對運載火箭多級飛行的特點，在傳統(tǒng)單級迭代制導(dǎo)方程的基礎(chǔ)上，進一步推導(dǎo)了多級迭代制導(dǎo)方程；茹家欣[13]利用最優(yōu)控制原理，從火箭簡化運動方程出發(fā)，以火箭推力方向的3分量為控制變量推導(dǎo)了迭代制導(dǎo)方法；池賢彬等[14]利用凸優(yōu)化技術(shù)簡化航天器的相對運動動力學(xué)模型，并通過迭代制導(dǎo)獲得追蹤航天器的制導(dǎo)策略。

進一步，在控制對象的模型復(fù)雜性和最優(yōu)控制必要條件的推導(dǎo)方式等方面，現(xiàn)有文獻也進行了改進研究。Lu等[15]結(jié)合最優(yōu)控制原理和多級打靶法推導(dǎo)了運載火箭的多級點火制導(dǎo)算法；針對大氣層內(nèi)火箭受力的復(fù)雜情況，Lu在文獻[16,17]中進一步推導(dǎo)了多級點火制導(dǎo)算法；傅瑜等[18]通過計算終端約束對協(xié)態(tài)變量的雅克比矩陣，獲得了解析求解約束方程的迭代制導(dǎo)方法；鄭旭等[19]推導(dǎo)了火箭在大氣層外的解析動力學(xué)模型，將共軛狀態(tài)向量和飛行時間作為迭代變量，給出了多終端約束下的迭代制導(dǎo)算法；鄧逸凡等[20]研究了適用于航天器空間變軌任務(wù)的迭代制導(dǎo)算法，直接以軌道根數(shù)為終端約束條件建立邊界條件；李超兵等[21]在入軌點軌道坐標(biāo)系下對制導(dǎo)的開關(guān)機點優(yōu)化，進一步得到改進的迭代制導(dǎo)方法。

現(xiàn)有文獻雖然從制導(dǎo)適應(yīng)性上對傳統(tǒng)迭代制導(dǎo)作出了種種改進，但很少直接從軌道根數(shù)的約束特性出發(fā)對制導(dǎo)算法進行設(shè)計，從而難以應(yīng)用于航天器空間變軌的一般情形。如文獻[17,18]以位置速度大小、飛行路徑角為終端約束；文獻[19,21]以位置和速度分量為終端約束；文獻[20]雖然直接針對軌道根數(shù)約束，但對乘子變量的消去處理方式復(fù)雜，不夠直觀，且沒有給出一般橢圓軌道情形下的約束方程形式。

考慮到上述文獻的不足，本文從對地心慣性坐標(biāo)系下航天器的運動模型出發(fā)，利用最優(yōu)控制原理得到位置速度與協(xié)態(tài)變量初值的關(guān)系式；進一步，針對軌道根數(shù)特性，推導(dǎo)了除真近點角外的5個軌道根數(shù)約束方程，并利用終端約束中位置速度和軌道根數(shù)的關(guān)系，以及協(xié)態(tài)變量的尺度特性得到另外兩個約束方程。通過直接求解7個完整約束方程組獲得協(xié)態(tài)變量初值，進而得到最優(yōu)推力方向。仿真結(jié)果表明了所提制導(dǎo)方法的有效性。

1 最優(yōu)制導(dǎo)問題描述

考慮有限推力大小的情形，在地心慣性坐標(biāo)系下，航天器的運動模型為

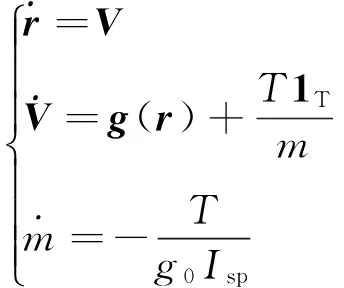
(1)

式中：r為位置；V為速度；g(r)為r處的地球引力加速度矢量；T為發(fā)動機推力大小；1T為單位矢量，表示發(fā)動機推力方向；m為航天器質(zhì)量；g0為在參考半徑R0(可取地球橢球模型的長半軸)處的標(biāo)準(zhǔn)重力加速度；Isp為發(fā)動機比沖(采用重量描述，單位為s)。

考慮到發(fā)動機點火持續(xù)時間通常在幾百秒以內(nèi)，航天器的運動量在整個軌道變化范圍內(nèi)可以看作小量，因此g(r)可采用式(2)近似：

(2)

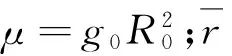
(3)

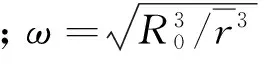
(4)

制導(dǎo)的終端約束通常由關(guān)于終端位置rf和終端速度Vf的k(k≤6)個等式約束組成：

φ(rf,Vf)=0

(5)

為節(jié)省燃料，推力方向1T可通過求解使得下面指標(biāo)最小的最優(yōu)控制問題來獲得：

(6)

注意式(6)中以當(dāng)前瞬時時刻為0時刻；τf=tf/tref，tf為終端時刻。整個制導(dǎo)的思路是：在每一個制導(dǎo)解算周期內(nèi)，通過迭代求解式(3)～式(6)組成的最優(yōu)控制問題來獲得最優(yōu)推力方向1T,隨著飛行時間的增加，實際位置與終端約束的位置越來越靠近，因此對引力加速度的近似誤差也會越來越小。

根據(jù)最優(yōu)控制理論，選擇如下哈密頓函數(shù)：

H0+TF

(7)

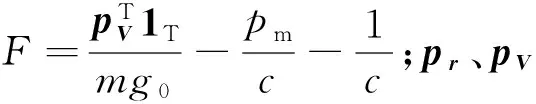
(8)

注意式(8)中的求導(dǎo)運算同樣是相對于無量綱化時間τ而言的。

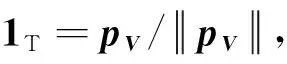
設(shè)pr的初值為pr0,當(dāng)前瞬時時刻的位置和速度分別為r0和V0,根據(jù)式(8)有

(9)

式(9)為關(guān)于pV和-pr/ω的線性微分方程，其解為

(10)

將式(10)進一步展開可得

(11)

根據(jù)式(3)有

(12)

定義

(13)

(14)

式中：

則式(12)的解可寫為

(15)

根據(jù)數(shù)值積分公式，有

(16)

(17)

式中:各ic和is的值均可根據(jù)式(11)來確定。因此有

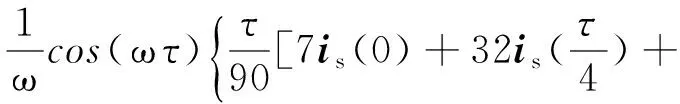
(18)

V(τ)=-ωsin(ωτ)r0+cos(ωτ)V0+cos(ωτ)·

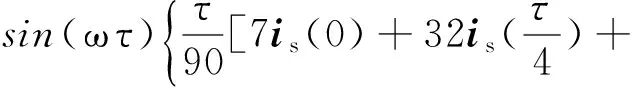
(19)

可見，在當(dāng)前瞬時時刻位置和速度確定的前提下，pr(τ)、pV(τ)、r(τ)和V(τ)均為協(xié)態(tài)變量初值pr0和pV0的函數(shù)，而實際最終的位置和速度還取決于τf,一共有7個未知變量，如果能夠構(gòu)造關(guān)于pr0、pV0和τf的7個方程，則求解這個方程就能獲得pV0,從而得到最優(yōu)推力方向。

2 約束方程構(gòu)造

在發(fā)動機推力大小T不可調(diào)的前提下，理論上只能滿足5個終端約束，對于航天器入軌來說，通常選取軌道根數(shù)來描述入軌條件，形成以軌道根數(shù)描述的終端約束條件。經(jīng)典的6個軌道根數(shù)為半長軸a、偏心率e、軌道傾角i、升交點赤經(jīng)Ω、近地點幅角w、真近點角f,對應(yīng)的目標(biāo)量均用下角標(biāo)T表示，通常不約束真近點角，即選取的5個終端約束為半長軸aT、偏心率eT、軌道傾角iT、升交點赤經(jīng)ΩT和近地點幅角wT。

2.1 半長軸約束

由二體問題中的活力公式可知

(20)

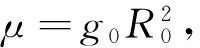
(21)

因此，半長軸的終端約束為

(22)

2.2 偏心率約束

φ2(rf,Vf)=

(23)

2.3 軌道傾角約束

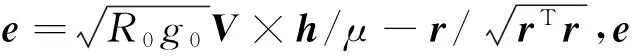
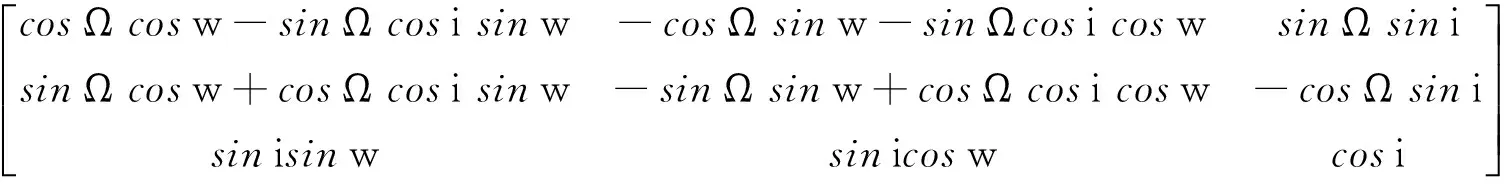
(24)

顯然，在慣性系中h方向的單位矢量為

(25)

(26)

2.4 升交點赤經(jīng)約束

根據(jù)2.3小節(jié)中的分析，升交點赤經(jīng)約束為

(27)

2.5 近地點幅角約束

偏心率矢量e在地心慣性坐標(biāo)系中的分量滿足：

(28)

從而有

(29)

(30)

從而有

(31)

結(jié)合式(28)、式(29)和式(31)可知，近地點幅角約束為

(32)

式中：

φ1～φ5構(gòu)成了關(guān)于rf和Vf的5個終端約束，為求解協(xié)態(tài)變量初值和飛行時間，還需要2個終端約束構(gòu)成完整的約束方程。

2.6 第6個約束方程

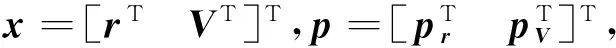
(33)

式中：zp為拉格朗日乘子向量，為避免數(shù)值求解困難，需要消去zp。通常的方法是求解下述方程:

(34)

得到關(guān)于rf和Vf的解y,則有

yTpf=0

(35)

式(35)構(gòu)成了第6個約束方程。

上述方法雖然直觀，但是實際求解式(34)，特別是獲得y的解析表達式并不容易，因此這里考慮另外一種思路。

由于位置速度和6個軌道根數(shù)之間可以互相轉(zhuǎn)換，rf和Vf可以表示為軌道根數(shù)的形式，因此φ1～φ5也可以表示成軌道根數(shù)的函數(shù)，即令η=[aeiΩwf]T,則終端約束可寫為

(36)

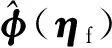
(37)

令y=?xf/?ff,則由式(35)可知第6個約束方程為

(38)

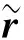
(39)

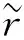
(40)

(41)

對式(39)微分可得

(42)

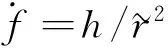
(43)

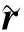
(44)

(45)

(46)

從而可知

(47)

比較式(43)和式(47)可得

(48)

(49)

進一步考慮無量綱位置和速度的情形，由式(48)和式(49)可得

(50)

(51)

因此有

(52)

從而式(38)可寫為

(53)

式(53)即為第6個約束方程。

2.7 第7個約束方程

由最優(yōu)控制原理，協(xié)態(tài)方程可寫為

(54)

(55)

可見，哈密頓函數(shù)也只是每一項進行了同樣的縮放，因此不會影響最優(yōu)推力方向的求解。因此，這里考慮針對協(xié)態(tài)變量的尺度設(shè)計第7個約束方程如下(選擇不唯一)：

(56)

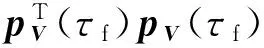
注：在獲得7個完整約束方程后，在每一次制導(dǎo)計算周期內(nèi)利用牛頓迭代法對方程進行求解獲得協(xié)態(tài)變量初值，即可得到最優(yōu)推力方向。在仿真程序中，牛頓迭代法求解方程組所需要的雅可比矩陣利用數(shù)值分析中常用的差商法獲得，因此計算量要大于傳統(tǒng)的迭代制導(dǎo)方法。與迭代制導(dǎo)類似，在一開始的幾次制導(dǎo)計算周期內(nèi)需要的迭代次數(shù)較多，后面基本迭代1～2次即可得到解。對于第3節(jié)仿真中的例子，在箭載計算機運行中程序時，完成一次制導(dǎo)指令解算所需的時間大約為5 ms。

3 仿真驗證

為驗證所提方法的有效性，針對航天器某一次變軌任務(wù)進行仿真驗證。設(shè)置航天器的初始質(zhì)量為8 680.554 8 kg，主發(fā)動機推力的大小為6 500 N，比沖為3 095 m/s，初始和目標(biāo)軌道根數(shù)如表1所示。

假設(shè)航天器的初始姿態(tài)已經(jīng)調(diào)整到合適位置，從初始位置開始即進行制導(dǎo)解算，不考慮前段累積偏差。仿真計算步長選為10 ms，考慮J2引力攝動項，終止姿態(tài)角迭代計算的條件選為剩余分析時間小于 5 s 時，關(guān)機條件為剩余飛行時間小于0.1 s時。

表1 航天器的初始和目標(biāo)軌道根數(shù)Table 1 Initial and target orbital elements of spacecraft

針對表1中的數(shù)據(jù)，將本文方法與文獻[20]中方法進行對比仿真，制導(dǎo)結(jié)果如圖1所示，本文方法的實際飛行時間為168.130 0 s，文獻[20]中方法的實際飛行時間為168.670 0 s。

由圖1中的仿真結(jié)果可以看出，在整個制導(dǎo)過程中，兩種方法均能保證剩余時間逐漸減小到0，除真近點角外的5個軌道根數(shù)誤差最終也趨于0，制導(dǎo)結(jié)束后的偏差數(shù)據(jù)如表2所示。

由表2可知，2種方法均能保證航天器最終到達的軌道與目標(biāo)軌道根數(shù)的偏差在容許范圍內(nèi)，且與文獻[20]中方法相比，本文方法的軌道根數(shù)偏差更小，如果需要進一步減小某個軌道根數(shù)偏差，可對該軌道根數(shù)的約束方程進一步進行加權(quán)，如若需要進一步減小偏心率偏差，則可根據(jù)式(23)，在程序中令φ2=γφ2,γ為大于1的數(shù)，如取為10、100等。

進一步，假設(shè)推力和比沖等各偏差均服從正態(tài)分布，對應(yīng)的3σ偏差值如表3所示。進行1 000次打靶仿真，最終得到的軌道根數(shù)偏差如圖2所示。

圖1 本文方法和文獻[20]中方法的制導(dǎo)結(jié)果仿真對比Fig.1 Simulation comparion of guidance results between proposed method and method in Ref.[20]

方法半長軸偏差/m偏心率偏差軌道傾角偏差/(°)升交點赤徑偏差/(°)近地點幅角偏差/(°)本文方法-22.0731-9.7929×10-5-4.9592×10-52.7294×10-51.5200×10-2文獻[20]方法345.3752-1.7219×10-4-7.6690×10-52.0290×10-42.2500×10-2

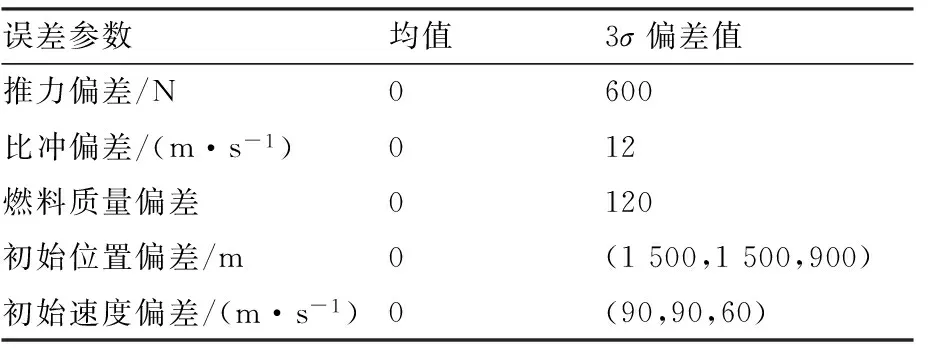
表3 誤差參數(shù)3σ偏差值Table 3 3σ deviation values of error parameters

從圖2可以看出，對于表3中的誤差條件，半長軸偏差最大為200 m，偏心率偏差最大為8.0×10-4，軌道傾角和升交點赤經(jīng)偏差最大為4×10-4(°)，近地點幅角偏差最大為0.15°。此外，各軌道根數(shù)偏差參數(shù)均集中在零附近，仿真結(jié)果表明本文所提制導(dǎo)算法對于偏差具有一定的適應(yīng)性。

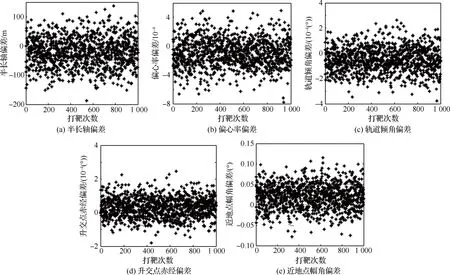
圖2 軌道根數(shù)統(tǒng)計偏差Fig.2 Statistical error of orbital element

4 結(jié) 論

本文直接從地心慣性坐標(biāo)系下航天器的運動模型出發(fā)，將制導(dǎo)指令求解問題轉(zhuǎn)化為約束方程組的構(gòu)造與求解問題，并進行了相應(yīng)的仿真分析。

1) 不需要假設(shè)制導(dǎo)指令角的形式，適用范圍大于傳統(tǒng)的迭代制導(dǎo)。

2) 從最優(yōu)控制理論出發(fā)求解制導(dǎo)指令，具有一定的最優(yōu)性。

3) 所提方法能夠保證航天器最終到達的軌道與目標(biāo)軌道根數(shù)的偏差在容許范圍內(nèi)，且對于偏差具有一定的適應(yīng)性。

[1] CHEN S Y, XIA Q L. A Multiconstrained ascent guidance method for solid rocket-powered launch vehicles[J]. International Journal of Aerospace Engineering, 2016(1):1-11.

[2] QUADRELLI M B, WOOD L J, RIEDEL J E, et al. Guidance, navigation, and control technology assessment for future planetary science missions[J]. Journal of Guidance, Control, and Dynamics, 2015, 38(7): 1165-1186.

[3] VACHON A, DESBIENS A, GAGNON E, et al. Launch ascent guidance by discrete multi-model predictive control[J]. Acta Astronautica, 2014, 95: 101-110.

[4] HULL D G, HARRIS M W. Optimal solutions for quasiplanar ascent over a spherical Moon[J]. Journal of Guidance, Control and Dynamics, 2012, 35(4): 1218-1223.

[5] LU P, FORBES S, BALDWIN M. A versatile powered guidance algorithm[C]∥AIAA Guidance, Navigation, and Control Conference. Reston, VA: AIAA, 2012: 4843-4858.

[6] JEB S O, JOHN H W, TANNEN S V, et al． Space launch system ascent flight dontrol design[DB/OL].http:∥ntrs.nasa.gov/archive/nasa/casi.ntrs.nasa.gov/20140008731.pdf．

[7] LAN X J, LIU L, WANG Y J. Online trajectory planning and guidance for reusable launch vehicles in the terminal area[J]. Acta Astronautica, 2016, 118: 237-245.

[8] HALBE O, RAJA R G, PADHI R. Robust reentry guidance of a reusable launch vehicle using model predictive static programming[J]. Journal of Guidance, Control, and Dynamics, 2014, 37(1): 134-148.

[9] SONG E J, CHO S, ROH W R. A comparison of iterative explicit guidance algorithms for space launch vehicles[J]. Advances in Space Research, 2015, 55(1): 463-476.

[10] TIAN B, FAN W, SU R, et al. Real-time trajectory and attitude coordination control for reusable launch vehicle in reentry phase[J]. IEEE Transactions on Industrial Electronics, 2015, 62(3): 1639-1650.

[11] LU B, CUI N, FU Y, et al. Closed-loop atmospheric ascent guidance based on finite element method[J]. Aircraft Engineering and Aerospace Technology: An International Journal, 2015, 87(5): 393-401.

[12] 陳新民, 余夢倫. 迭代制導(dǎo)在運載火箭上的應(yīng)用研究[J]. 宇航學(xué)報, 2003, 24(5): 484-489.

CHEN X M, YU M L. Study of iterative guidance application to launch vehicles [J]. Journal of Astronautics, 2003, 24(5): 484-489 (in Chinese).

[13] 茹家欣. 液體運載火箭的一種迭代制導(dǎo)方法[J]. 中國科學(xué)E輯:技術(shù)科學(xué), 2009, 39(4): 696-706.

RU J X. An iterative guidance method for liquid launch vehicle[J]. Science in China Series E: Technological Sciences, 2009, 39(4): 696-706 (in Chinese).

[14] 池賢彬, 岳曉奎, 李鵬. 基于凸優(yōu)化的自主交會迭代制導(dǎo)方法[J]. 中國空間科學(xué)技術(shù), 2014(1): 26-34.

CHI X B, YUE X K, LI P, et al. Iterative guidance method of autonomous rendezvous based on convex optimization[J]. Chinese Space Science & Technology, 2014(1): 26-34.

[15] LU P, GRIFFIN B J, DUKEMAN G A, et al. Rapid optimal multiburn ascent planning and guidance[J]. Journal of Guidance, Control, and Dynamics, 2008, 31(6): 1656.

[16] LU P, SUN H, TSAI B. Closed-loop endoatmospheric ascent guidance[J]. Journal of Guidance Control and Dynamics, 2003, 26(2): 283-294.

[17] LU P, PAN B. Highly constrained optimal launch ascent guidance[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(2): 404-414.

[18] 傅瑜, 陳功, 盧寶剛,等. 基于最優(yōu)解析解的運載火箭大氣層外自適應(yīng)迭代制導(dǎo)方法[J]. 航空學(xué)報, 2011, 32(9): 1696-1704.

FU Y, CHEN G, LU B G, et al. A vacuum adaptive iterative guidance method of launch vehicle based on optimal analytical solution[J]. Acta Aeronautica et Astronautica Sinica, 2011, 32(9): 1696-1704 (in Chinese).

[19] 鄭旭, 高長生, 陳爾康,等. 一種基于大氣層外解析動力學(xué)模型的最優(yōu)迭代制導(dǎo)方法[J]. 西北工業(yè)大學(xué)學(xué)報, 2016, 34(6):1093-1100.

ZHENG X, GAO C S, CHEN E K, et al. An optimal iterative guidance method based on exoatmospheric analytical dynamic model [J]. Journal of Northwestern Polytechnical University, 2016, 34(6): 1093-1100 (in Chinese).

[20] 鄧逸凡, 李超兵, 王志剛. 一種基于軌道要素形式終端約束的航天器空間變軌迭代制導(dǎo)算法[J]. 航空學(xué)報, 2015, 36(6): 1975-1982.

DENG Y F, LI C B, WANG Z G. An iterative guidance algorithm using orbital elements as terminal constraints for spacecraft orbit transfer [J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(6): 1975-1982 (in Chinese).

[21] 李超兵, 王晉麟, 李海. 一種基于多終端約束的最優(yōu)制導(dǎo)方法[J]. 中國空間科學(xué)技術(shù), 2016, 36(5): 9-17.

LI C B, WANG J L, LI H. An optimal guidance method based on multiple terminal constraints[J]. Chinese Space Science and Technology, 2016, 36(5): 9-17 (in Chinese).