路網宏觀基本圖中磁滯現象的產生機理

王鵬飛，岳 昊，關宏志

(1.河北科技師范學院城市建設學院，河北秦皇島066004；2.北京工業大學交通工程北京市重點實驗室，北京100124；3.北京交通大學城市交通復雜系統理論與技術教育部重點實驗室，北京100044)

0 引言

為了實時把握路網中車輛的運行狀態，進而對交通流進行誘導與控制，交通工程師在道路網中布設了各式各樣的檢測器(例如線圈檢測器、浮動車等)。但管理者想通過各路段上零散的交通信息把握路網整體的車輛運行狀態依舊十分困難，這是非線性的交通流現象與出行者路徑選擇行為相互作用的結果[1]。

對此，文獻[2]提出可以表征路網車輛數與路網總流量之間函數關系的路網宏觀基本圖(Macroscopic Fundamental Diagram,MFD)的概念。文獻[3]通過對日本橫濱商業中心的檢測器數據進行分析，驗證了MFD在真實城市道路網中的存在。近年來，針對法國圖盧茲[4]、美國明尼蘇達州[5]、波特蘭[6]、芝加哥與爾灣[7]高速公路網絡的研究發現，MFD會產生磁滯現象。同時，以中國北京[8-10]、上海[11-12]和日本仙臺[13]、京都[14]的城市道路網為研究對象，也發現MFD會產生磁滯現象。其中，文獻[13-14]使用1年的交通檢測器數據驗證了MFD中磁滯現象在一定條件下出現的穩定性。

針對MFD中磁滯現象的產生機理，在理論研究方面，文獻[15-16]通過仿真實驗，揭示了交通密度在時空上的不均勻分布是MFD出現磁滯現象的關鍵原因；文獻[17]以2環模型從理論上給出了MFD中磁滯現象的產生條件。在實證研究方面，文獻[5]使用檢測器數據發現在出行高峰時段過后的一段時間內，路網中會出現車輛在空間上分布不均衡的現象；文獻[8-9]認為高峰時段前后不同的車道變換率是產生磁滯現象的重要原因；文獻[12]發現各個檢測器檢測到的交通狀態并非同步，認為這是MFD磁滯現象產生的重要原因；此外，文獻[14,18]以1年的檢測器數據驗證了文獻[15-16]結論的正確性，即在同一平均交通密度下的交通密度標準差與平均流量之間呈現線性負相關。

但至今為止，鮮有研究從路網中高峰時段前后交通流狀態演變的角度去揭示磁滯現象的產生機理并對其存在的普遍性進行說明，而這是將MFD應用于實際交通管控中的重要環節。現階段，基于MFD的路網流入流出量控制策略(國內外代表研究見文獻[19-20])全部以區域內存在明確路網宏觀基本圖(well-defined MFD)為前提，而這與大量的現實觀測情況并不相符。

鑒于此，本文以存在單一交通瓶頸的、由若干同質路段串聯而成的交通網為對象，利用車流波動理論從交通流狀態演化的角度，對MFD中磁滯現象的產生機理及其存在的普遍性進行分析，并以日本京都市的實際觀測數據來驗證理論分析得到結論的可靠性。

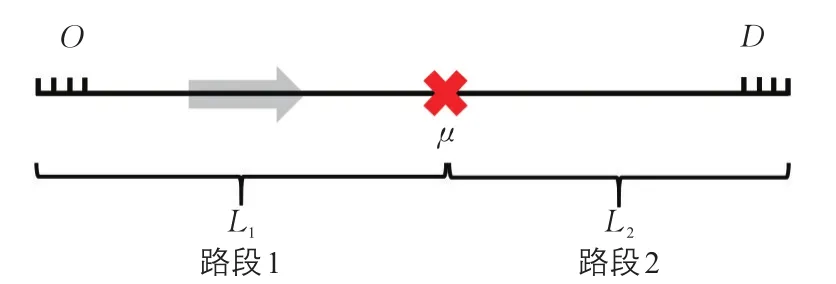
圖1 交通網Fig.1 Roadway network

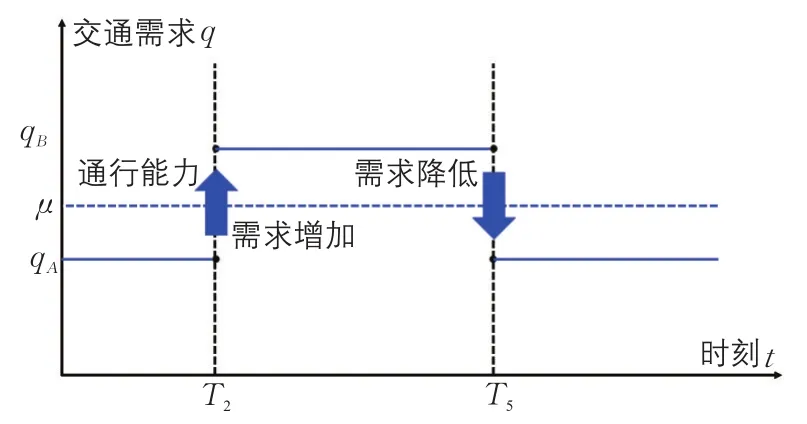
圖2 交通需求時變圖Fig.2 Time-vary diagram of transportation demand

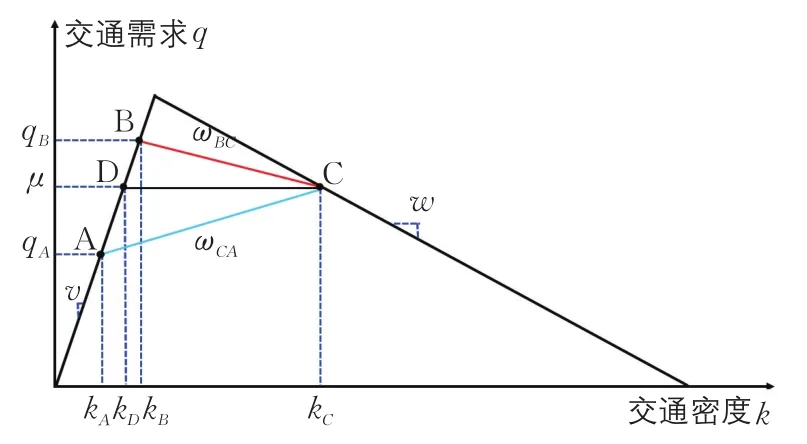
圖3 每個路段的交通基本圖Fig.3 Fundamental diagram for different roadway segment

1 模型建立

1.1 路網結構與交通需求的設定

所有車輛從O點(居住地)出發向D點(商業中心)移動，且在此過程中存在通行能力為μ的交通瓶頸(瓶頸可視為真實路網中的平面交叉口或通行能力較低的路段)，從O到瓶頸的部分稱為路段1，而從瓶頸到D的路段為路段2(見圖1)。上游的交通需求在T2時刻由qA(qA＜μ)增加至(qB(qB＞μ))，而后在T5時下降至qA(見圖2)，此設定反映了(早晚)高峰時段前后的交通需求時變特性。路段1表示路網中在瓶頸上游受到擁堵流影響的路段，路段2代表在瓶頸下游未受到擁堵流影響的路段。此外，各路段的交通基本圖如圖3所示。

1.2 路網交通狀態的演變過程

在上述設定的路網結構與交通需求的條件下，路網中交通狀態的演化過程可由時空圖(見圖4)表示。其中，各交通流狀態(A,B,C,D)的交通量與交通密度可由下列公式計算得出：qA=kAv，qB=kBv，qD=μ=kDv，qC=μ。另外，沖擊波ωBC與ωCA的波速為

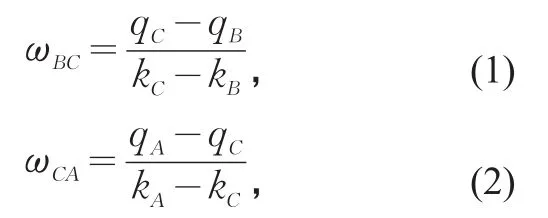
式中：qA，qB，qC為交通流狀態A，B，C的交通量；kA，kB，kC為交通流狀態A，B，C的交通密度。

由此可知，每一時段內路網中存在的交通流狀態不盡相同，并且每一種狀態所覆蓋的路段數量與長度也不同。

2 MFD中磁滯現象產生機理

2.1 MFD的定義

MFD表征路網總流量P(t)與路網車輛數N(t)之間的函數關系，即

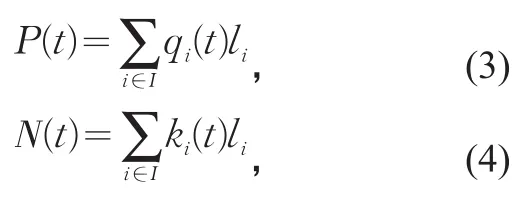
式中：li為第i條路段的長度/km；qi(t)為第i個檢測器在時段t內檢測到的交通量/(輛·5 min-1)；ki(t)為第i個檢測器在時段t內檢測到的平均交通密度/(輛·km-1)。

根據上述定義，要求解每一時段的MFD，必須首先計算每種交通流狀態在路網中所占有的路段總長度l(t)。例如，在時段⑤，路網中存在三種交通流狀態：B，C與D(見圖4)，它們的分布如圖5所示，因此，路網總流量與路網車輛數分別為

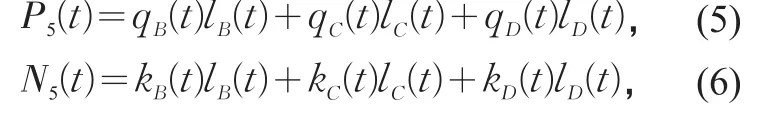
式中：交通量qC=qD=μ。

2.2 各時段的MFD及其變化趨勢

根據上述MFD的定義(公式(3)，(4))計算得出的每一時段的路網總流量與路網車輛數，并通過對計算結果進行判別，得出每一時段的路網總流量與路網車輛數的變化趨勢(見表1和表2)。其中，時段④的路網總流量與時段⑥的路網車輛數的變化趨勢因無法從符號判定，所以需要分情況討論，結果如表3與表4所示。

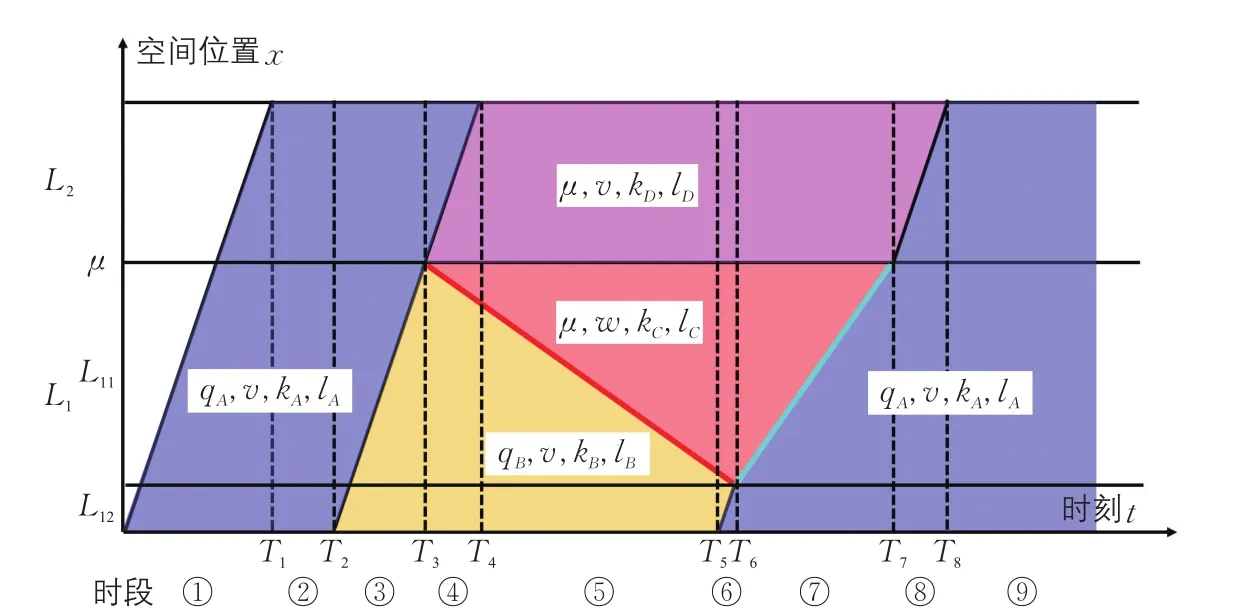
圖4 時空圖Fig.4 Time-space diagram

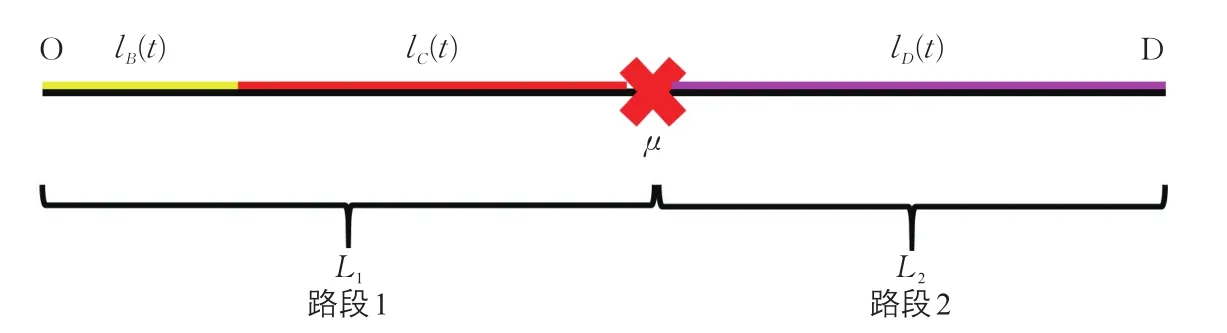
圖5 時段⑤交通流狀態的空間分布Fig.5 Spatial distribution of traffic flow state in roadway network during time period⑤

表1 路網總流量及其變化趨勢Tab.1 Total traffic flow and its variation trend

表2 路網車輛數及其變化趨勢Tab.2 Total number of vehicles and its variation trend

將表1～表4中的計算結果反映在MFD(見圖6)上則可明顯的發現，在此模型的設定(存在交通瓶頸，并且高峰時段的交通量超過瓶頸容量)下MFD一定會出現磁滯現象，其中，時段④與時段⑥的變化趨勢雖具有不確定性(圖6中的紅線)，但這些不確定性并不影響磁滯現象的出現。

2.3 磁滯現象的產生機理

首先，需要對磁滯環形成過程(時段④與⑤，上環用U表示)與消除過程(時段⑦與⑧，下環用L表示)中的路網總流量及路網車輛數的取值范圍，路網中存在的交通流狀態進行比較分析。

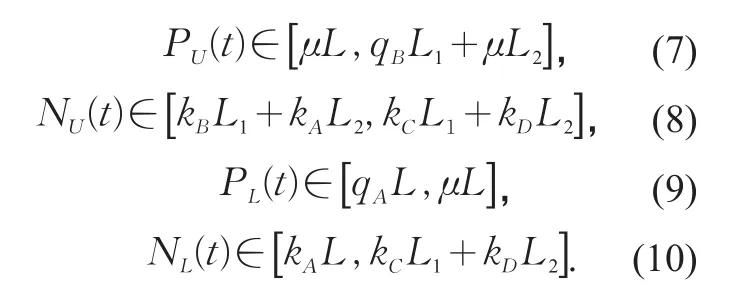
表3 時段④路網總流量的變化趨勢Tab.3 Variation trend of total traffic flow during time period④

表4 時段⑥路網車輛數的變化趨勢Tab.4 Variation trend of number of vehicles during time period⑥

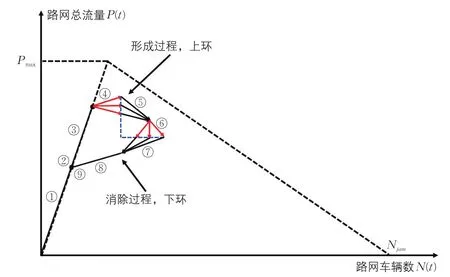
圖6 路網宏觀基本圖的形狀特征分析Fig.6 Characteristics of macroscopic fundamental diagram of roadway network

表5 磁滯環形成與消除過程中交通流狀態的演變Tab.5 Evolution of traffic flow state in loading and recovery process in the hysteresis loop

雖然兩個過程中的路網車輛數的取值范圍有所重合，但上環的路網總流量卻總是大于等于下環，即PU(t)≥PL(t)。

對比公式(7)與公式(9)即可發現產生此結果的關鍵原因是因為磁帶環在消除過程中缺少低密度、高流量的交通流狀態B。從磁滯環形成與消除過程中的交通流狀態演變過程(見表5)分析，在時段④⑤時，交通流狀態B逐漸被向上游蔓延的交通流狀態C(擁堵流)所代替。而當路網的交通需求開始下降后(時段⑥以后)，交通流狀態A(低流量、低密度)逐漸開始取代狀態B與狀態C。因此，狀態B的缺失是出行高峰時段的擁堵傳播(擁堵溢出點增加)與出行高峰過后的出行者需求降低這兩個原因接連作用的結果，非人為強制干預(即恢復、增加路網容量的交通管制措施，例如交通事故處理完畢或公交專用車道恢復為普通行車道等交通管制措施[21])不可避免，這也就是為什么在很多城市路網的MFD中都可觀測到磁滯現象(見引言部分)的重要原因。

進一步對比磁滯環的形成過程與消除過程中存在的交通流狀態即可發現：在消除過程中，低密度、低流量的交通流狀態A與擁堵流狀態C同時存在，即路網中交通密度在空間上的分布(相較形成過程)是不均勻的。此結論與文獻[5,14]中出行高峰前后交通密度在空間上的分布觀測結果相一致，從理論上闡述了此現象出現的機理。

此外，在同一路網車輛數的條件(公式(11))下，進一步定量分析磁滯環在形成與消除過程中的路網交通流狀態，即可得到lC,U(t)＜lC,L(t)的結論。即在同一路網車輛數的條件下，在磁滯環消除過程中，擁堵狀態C所占據的路段總數量更多、總長度更長。而在真實路網中，這意味著在比較相同路網車輛數條件下的擁堵模式時，會發現在磁滯環的消除過程中存在更多的擁堵路段與擁堵溢出點。此結論與文獻[14-15]中仿真實驗所得結果相符。

3 實例分析

大城市路網中MFD某種特征的產生機理受到交通數據采集方式、檢測器的數量與位置以及眾多因素的影響。本文以日本京都市為例，以實際的檢測器數據對上述理論分析的可靠性進行驗證，并非以研究京都市路網中MFD磁滯現象的真正產生機理為目的。

3.1 京都市道路網中的路網宏觀基本圖

京都市是日本的古都也是著名的旅游勝地，截至2013年10月人口約147萬。路網中的單向路段由1～3條車道組成，道路交叉口間距為100～500 m。在城市路網中分布著約800個檢測器，記錄各路段每5 min的斷面交通量與車速[14]。在剔除錯誤數據后，利用公式q=kv即可得到交通密度，再依照公式(3)，(4)計算每5 min的路網總流量與路網車輛數即得到路網宏觀基本圖。研究發現在每年①11月(紅葉觀光季節)的周末，京都市的MFD(見圖7)都會呈現如下兩個特點：1)具有一個巨大的磁滯環；2)在磁滯環形成的過程中(13:00—17:15)會出現罕見②的水平推移現象(即磁滯環在形成過程中路網車輛數持續增加、但路網總流量保持不變的現象)。

3.2 磁滯現象分析

在對磁滯現象進行分析前，首先需要對路網中的擁堵溢出數St進行定義。

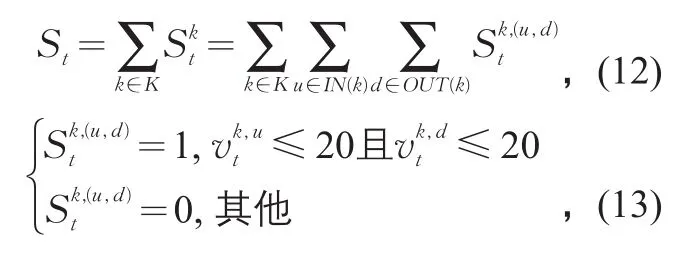
式中：K為路網中交叉口的集合；IN(k)，OUT(k)為交叉口k的上游流入與下游流出路段的集合；為交叉口k上游與下游路段的車速；為交叉口k處擁堵溢出點的個數。根據此定義，在時段t，某一交叉口處上游與下游路段同時陷入擁堵狀態時，則計算為1個擁堵溢出點。本文將時段t的平均車速小于等于20 km·h-1的路段定義為擁堵路段。

依據公式(12)，(13)對全天每5 min整個路網中擁堵溢出點的數量進行計算，發現在同一路網車輛數的條件(Nt≈8 250，t=13:00與t=18:55，見圖7)下，擁堵溢出點數量在磁滯環形成過程中為15，而在消除過程中為29(見圖8)。此實證結果驗證了2.3節理論分析得到的結論：在同一路網車輛數中，相較形成過程，磁滯環在消除過程中會擁有更多的擁堵溢出點。

3.3 水平推移現象分析

對于京都市MFD中產生的水平推移現象，文獻[14]并未從理論角度闡述其產生機理及意義。根據2.2節的理論分析，只要滿足 表 3 中 (μ-qA)v+(μ-qB)ωBC=0 這 一條件，即交通流狀態D代替狀態A導致的路網總流量的增加量與狀態C代替狀態B導致的路網總流量的減少量時刻等同，則會出現水平推移現象。

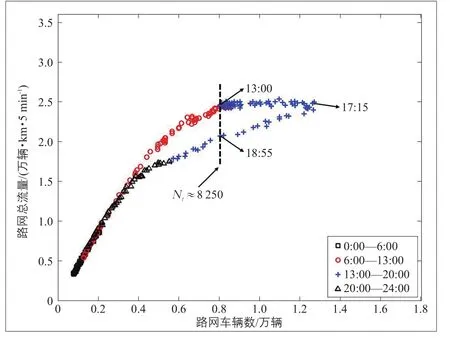
圖7 京都市紅葉觀賞季周末的MFDFig.7 Macroscopic fundamental diagram in Kyoto roadway networks on weekends during the autumn maple viewing

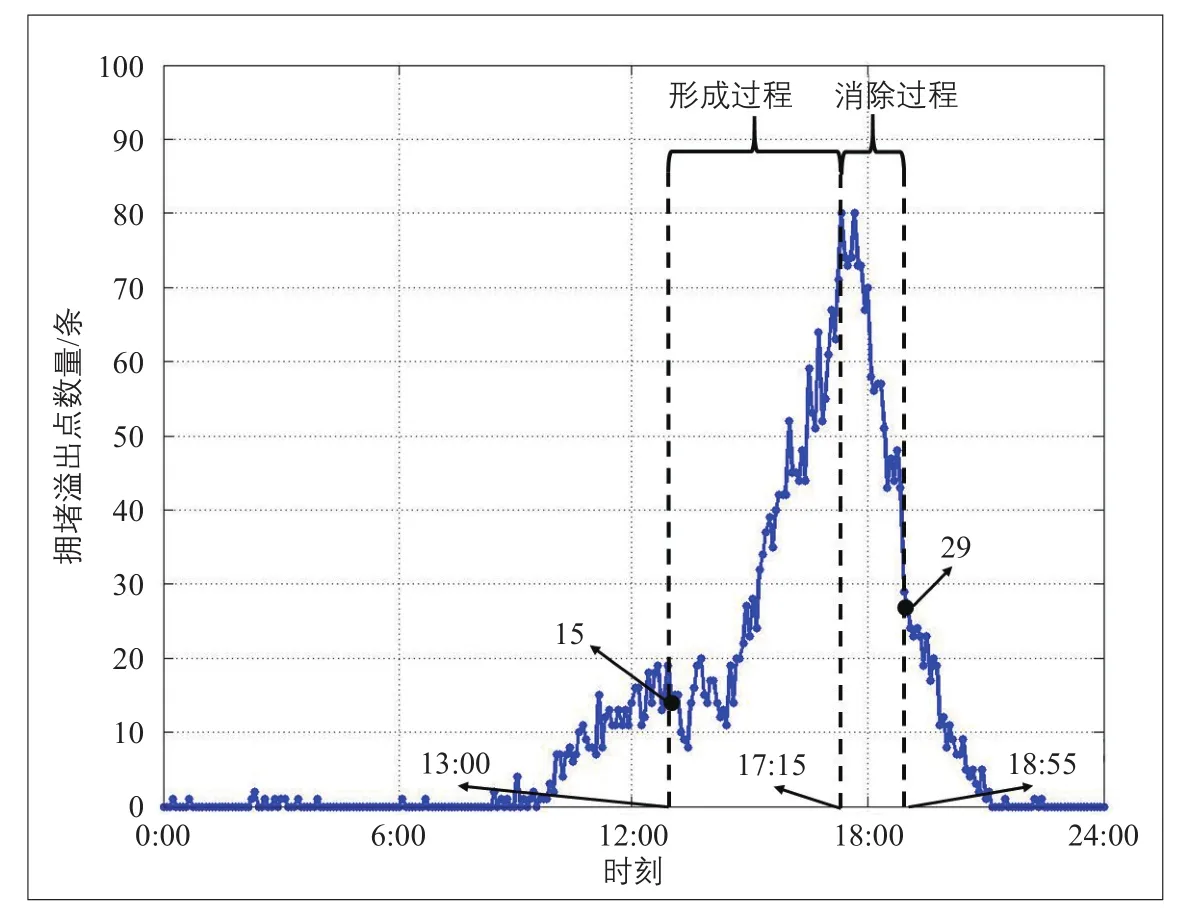
圖8 擁堵溢出點數量的推移Fig.8 Time-vary of the number of congestion spillover spots

在真實路網中，狀態A轉化為狀態D，意味著路網中不斷增加的車輛選擇了非擁堵路段(即擁堵可以回避，圖1中路段2上的車輛)，從而使得非擁堵路段的路網總流量(圖9a中的藍線)上升，接近其交通容量。相反，狀態C代替狀態B意味著車輛選擇了擁堵路段(即擁堵無法回避，圖1中路段1上的車輛)，使得擁堵路段的路網總流量(圖9a中的紅線)下降，低于交通容量。但無論怎樣，路網中車輛總數的增加總會使得擁堵路段與非擁堵路段的車輛數上升(見圖9b)，若兩種選擇使得路網總流量保持基本不變就會出現水平推移現象。此條件意味著路網中存在非擁堵路段可供不斷增加的車輛選擇，而這即是京都市MFD中出現水平推移現象的直接原因。上述分析是否符合實際路網中出行者的路徑選擇行為還有待考證。

4 結語

本文利用車流波動理論，從交通流狀態演化的角度闡述了MFD中磁滯現象的產生機理并得出以下結論：1)低密度、高流量的交通流狀態B經過擁堵流狀態C后逐漸被低密度、低流量的交通狀態A所代替，是磁滯現象產生的重要原因；2)在相同路網車輛數的前提下，磁滯環的消除過程將會產生更多的擁堵路段及擁堵溢出點；3)路網中尚存在非擁堵路段可供逐漸增加的車輛選擇是MFD中水平推移現象產生的必要條件。以日本京都市的實際觀測數據驗證了上述部分理論分析的可靠性。

未來，可以從以下幾個方面進行拓展研究：1)追加考慮道路網布局、OD的空間分布特性；2)追加考慮絕對理性或有限理性視野下的出行者路徑選擇行為[22]；3)探討網絡交通流逐日動態演化[23]與MFD特性再現的關系等。此外，本文以存在單一交通瓶頸、屬性相同的路段組成的串聯路網為對象得到MFD中磁滯現象產生的機理及特性，在應用于較大范圍路網時還有待進一步的嚴謹證明。

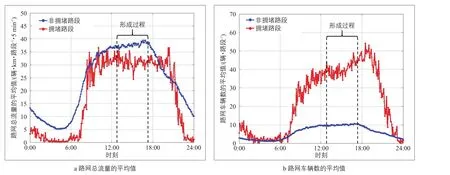
圖9 路網總流量與路網車輛數的平均值推移Fig.9 Time-vary of the average total traffic flow and number of vehicles

注釋：

Notes:

①在此僅展示具有代表性的2012年11月25日(周日，晴天)的路網宏觀基本圖。

②在至今為止關于MFD的實證或仿真研究中，尚未發現類似現象。

參考文獻：

[1]Daganzo C F.Queue Spillovers in Transportation Networks with a Route Choice[J].Transportation Science,1998,32(1):3-11.

[2]Daganzo C F.Urban Gridlock:Macroscopic Modeling and Mitigation Approaches[J].Transportation Research Part B,2007,41(1):49-62.

[3]Geroliminis N,Daganzo C F.Existence of Ur-ban-Scale Macroscopic Fundamental Diagrams:Some Experimental Findings[J].Transportation Research Part B,2008,42(9):759-770.

[4]Buisson C,Ladier C.Exploring the Impact of Homogeneity of Traffic Measurements on the Existence of Macroscopic Fundamental Diagrams[J].Transportation Research Record:Journal of the Transportation Research Board,2009,2124(12):127-136.

[5]Geroliminis N,Sun J.Hysteresis Phenomena of a Macroscopic Fundamental Diagram in Freeway Networks[J].Transportation Research PartA,2011,45(9):966-979.

[6]Saberi M,Mahmassani H S.Exploring Properties of Network Wide Flow-Density Relations in a Freeway Network[J].Transportation Research Record:Journal of the Transportation Research Board,2012,2315(16):153-163.

[7]Saberi M,Mahmassani H S.Hysteresis and CapacityDropPhenomenaFreewayNetworks:Empirical Characterization and Interpretation[J].Transportation Research Record:Journal of the Transportation Research Board,2013,2391(5):44-55.

[8]賀正冰，關偉，樊玲玲，等.北京市快速環路宏觀基本圖特征研究[J].交通運輸系統工程與信息，2014，14(2)：199-205.He Zhengbing,Guan Wei,Fan Lingling,et al.Characteristics of Macroscopic Fundamental Diagram for Beijing Urban Ring Freeways[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(2):199-205.

[9]He Zhengbing,He Shuyan,Guan Wei.A Figure-Eight Hysteresis Pattern in Macroscopic Fundamental Diagrams and Its Microscopic Causes[J].Transportation Letters,2015,7(3):133-142.

[10]朱琳，于雷，宋國華.基于MFD的路網宏觀交通狀態及影響因素研究[J].華南理工大學學報(自然科學版)，2012，40(11)：138-146.Zhu Lin,Yu Lei,Song Guohua.MFD-Based Investigation into Macroscopic Traffic Status of Urban Networks and Its Influencing Factors[J].Journal of South China University of Technology(Natural Science Edition),2012,40(11):138-146.

[11]姚崇富，付強，林航飛.上海快速路網宏觀基本圖特征研究[J].武漢理工大學學報(交通科學與工程版)，2016，40(3)：519-525.Yao Chongfu,Fu Qiang,Lin Hangfei.Research of Characteristics of Macroscopic Fundamental Diagram for Shanghai Expressway[J].Journal of Wuhan University of Technology(Transportation Science&Engineering),2016,40(3):519-525.

[12]付強，田光華，焦小龍.基于實際數據的宏觀基本圖磁滯現象及分析[J].城市道橋與防洪，2017(1)：125-128+132.Fu Qiang,Tian Guanghua,Jiao Xiaolong.Phenomenon and Analysis on Hysteresis of Macro Basic Graph Based on Actual Data[J].Urban Roads Bridges and Flood Control,2017(1):125-128+132.

[13]Wang P,Kentaro W,Akamatsu T,et al.An Empirical Analysis of Macroscopic Fundamental Diagrams for Sendai Road Networks[J].Interdisciplinary Information Sciences,2015,21(1):49-61.

[14]Wang P,Kentaro W,Akamatsu T,et al.Characterization of Macroscopic Fundamental Diagrams Based on Long-Term Detector Data[J].JSTE Journal of Traffic Engineering(in Japanese),2016,2(5):11-20.

[15]Mazloumian A,Geroliminis N,Helbing D.The Spatial Variability of Vehicle Densities as Determinant of Urban Network Capacity[J].Philosophical Transactions of Royal SocietyA,2010,368(1928):4627-4647.

[16]Mahmassani H S,Saberi M,Zockaie A.Urban Network Gridlock:Theory,Characteristics,and Dynamics[J].Transportation Research Part C,2013,36(11):480-497.

[17]Gayah V V,Daganzo C F.Clockwise Hysteresis Loops in the Macroscopic Fundamental Diagram:An Effect of Network Instability[J].Transportation Research Part B,2011,45(4):643-655.

[18]Knoop V L,Hoogendoorn S P.Empirics of a Generalized Macroscopic Fundamental Diagram for Urban Freeways[J].Transportation Research Record:Journal of the Transportation Research Board,2013,2391(13):133-141.

[19]Aboudolas K,Geroliminis N.Perimeter and Boundary Flow Control in Multi-Reservoir Heterogeneous Networks[J].Transportation Research Part B,2013,55(9):265-281.

[20]杜怡曼，吳建平，賈宇涵，等.基于宏觀基本圖的區域交通總量動態調控技術[J].交通運輸系統工程與信息，2014，14(3)：162-167.Du Yiman,Wu Jianping,Jia Yuhan,et al.MFD-Based Regional Traffic Volume Dynamic Control[J].Journal of Transportation Systems Engineering and Information Technology,2014,14(3):162-167.

[21]Wang P,Wada K,Akamatsu T.An Empirical Analysis on Macroscopic Fundamental Diagram for Urban Street Networks Based on Long-Term Detectors Data:Characteristics and Its Mechanism[C]//Transportation Research Board 96thAnnual Meeting,Washington DC,January 8-12,2017.

[22]劉詩序，關宏志，嚴海.網絡交通流動態演化的混沌現象及其控制[J].物理學報，2012，61(9)：58-67.Liu Shixu,Guan Hongzhi,Yan Hai.Chaotic Behavior in the Dynamical Evolution of Network Traffic Flow and Its Control[J].Acta Physical Sinica,2012,61(9):58-67.

[23]李濤，關宏志，梁科科.有限理性視野下網絡交通流逐日演化規律研究[J].物理學報，2016，65(15)：11-21.Li Tao,Guan Hongzhi,Liang Keke.Day-to-Day Dynamical Evolution of Network Traffic Flow Under Bounded Rational View[J].Acta Physical Sinica,2016,65(15):11-21.