高頻數據波動率小波估計方法的比較

盧小華，張艷慧，鄭宇軒

（北京工商大學 數學系，北京 100048）

0 引言

隨著金融高頻數據的普及，用小波分析方法對“原始信號”——金融高頻數據進行多分辨率分析，達到高頻處時間細分，低頻處頻率細分，進而估計其波動率的目的，具有很好的應用前景。此外，小波分析在計算機應用、信號處理、圖像分析等領域也有著廣泛應用。

目前已有許多學者對金融高頻數據的波動率進行研究，如Andersen等[1]提出的實際波動率及其改進[2]和Lunde等[3]提出的積分波動率的小波估計。實際波動率作為積分波動率的估計，開啟了對金融高頻數據波動率研究的熱潮；而由于金融高頻數據和小波分析中的信號具有相同的特性，因此可將收益率序列看成一輸入信號，從小波的角度來描述信號的波動問題。

秦喜文等[4]在小波估計基礎上利用5分鐘高頻交易數據，通過極大重疊離散小波變換方法對資產收益的積分波動率進行估計，克服了普通離散小波變換對樣本容量的限制問題。受此啟發，本文采用上證綜指1分鐘高頻交易數據，利用極大重疊離散小波變換方法對波動率進行估計，并與實際波動率估計方法進行比較，同時考察了不同采樣頻率下兩種估計方法的差異程度。

1 積分波動率的估計方法

1.1 小波分析方法

小波變換是空間和頻率的局部變換，可對函數或信號進行多尺度的細化分析，因而能有效地從信號中提取信息。極大重疊離散小波變換(MODWT)克服了離散小波變換(DWT)對樣本容量的限制問題，且由于沒有下采樣過程，在對非平穩時間序列分解時，能最大限度減少數據信息的遺失[4,5]。因此，本文采用極大重疊離散小波變換方法估計積分波動率。

設Pt是資產的對數價格過程，定義式（1）為[ ]t，t+1時間段的連續復合收益率。

假定資產對數價格Pt服從伊藤過程，即滿足：

這里μt和σt分別表示漂移項和擴散項，且均為隨機過程；ωt服從標準布朗運動。對式（2）兩側積分有：

其中等號右邊第一項來源于有限變差過程，第二項為伊藤積分，來源于局部鞅[6]。用表示由生成的σ-域，則有：

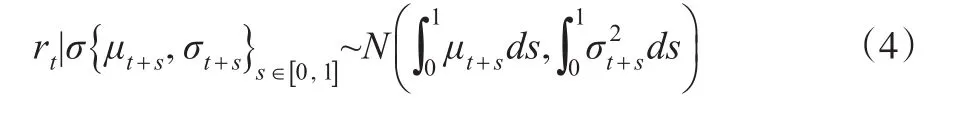
稱對數收益率rt的方差為[t，t+1] 時間段的積分波動率。它表明了在連續時間下價格波動的定義，故波動率在金融市場中具有重要的參考價值，因而對波動率進行準確估計是十分必要的。下面先簡單介紹一下積分波動率的小波估計方法。

令分別是極大重疊離散小波變換的第j層小波濾波器和尺度濾波器，長度為Lj=(2j-1)(L-1)+1。當j=1時，L1=L是單位尺度濾波器的長度，其中:

且{hj，l} ，{gj，l}是j級DWT小波濾波器和尺度濾波器。設X是一個N維向量，其元素為實值的時間序列{Xt，t=0，1，…，N-1}，其中N為任意整數，則X經過第j層極大重疊離散小波變換的小波系數向量和尺度系數向量分別為:

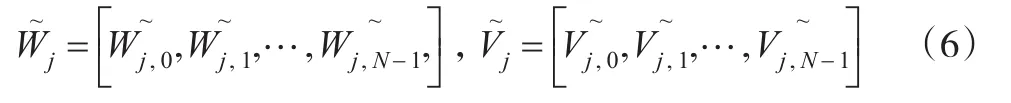
其元素分別為：

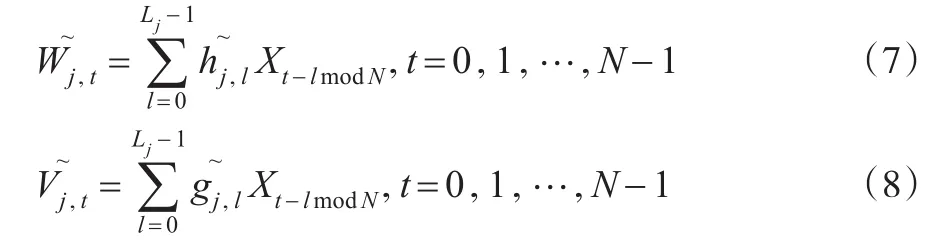
假設{Xt，t=…，-1，0，1，…} 是一個離散參數的實值隨機過程，則經過MODWT小波濾波器濾波后的隨機過程記為

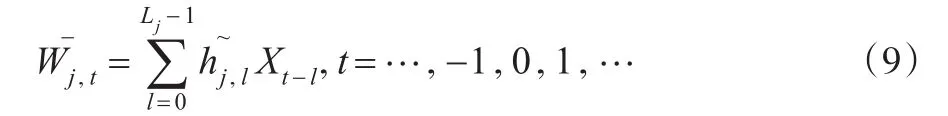
j波方差為：

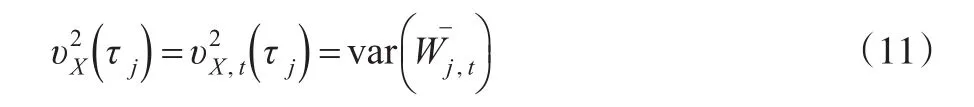
因而可以將過程{Xt}的方差依尺度τj分解，得到：

可知在尺度τj下小波方差越大，則對{Xt}總體方差的貢獻度越大，從而小波方差有助于在不同尺度下清晰地研究過程的波動持續性特征[8]，且當{Xt}非平穩，var(Xt)無窮大。

假設{Xt}是一個具有平穩d階后向差分的非平穩過程，{Xt，t=0，1，…，N-1} 是過程{Xt}的一個實現，在對小波方差進行估計時，本文選取長度為L(L≥2d)的小波濾波器，且當L足夠大時，滿足從而有：

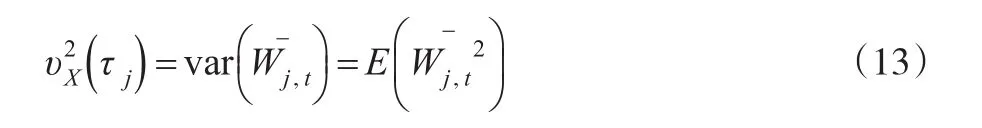
對于一組給定的含有dPt的n個觀測值的樣本，定義jn=[lo g2(n)-1]，則：

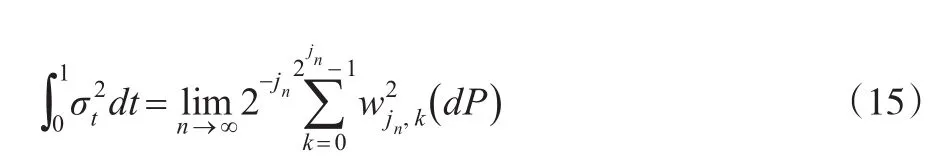
1.2 實際波動率

實際波動率也稱已實現波動率，定義式（16）為日對數收益率的實際波動率[10]。

其中rt，i表示第t天的第i個對數收益率，n為第t天的對數收益率的個數。

為了考慮[t，t+1]時間段內的收益波動，對[t，t+1] 進行離散劃分：

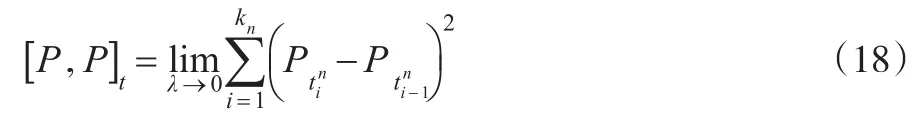
由于伊藤過程二次變差完全由伊藤積分貢獻，則利用伊藤積分二次變差有：

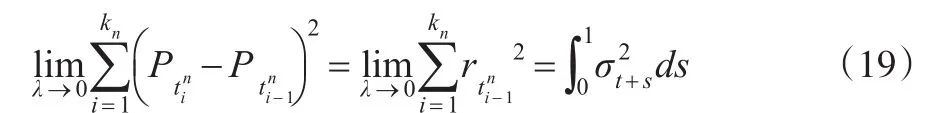
由式(19)可知，在時間間隔合理的條件下，實際波動率可用來估計積分波動率。

2 實證分析

本文選取上證綜指2016年4月18日至2016年10月21日正常交易時間的1分鐘高頻交易數據作為樣本，在計算對數收益率時，采用區間的最后一個交易價格作為該區間的股票價格，并選用Daubechies、Least Asymmetric、Coiflets、Haar這4種小波函數對對數收益率序列進行極大重疊離散小波變換，估計積分波動率。同時為了對比，本文也利用實際波動率來估計積分波動率。

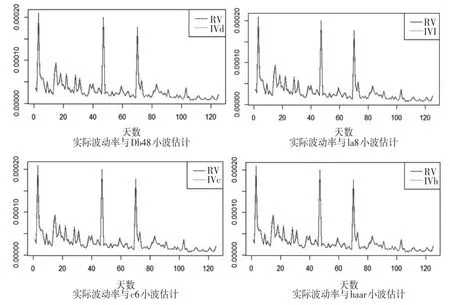
圖1 實際波動率與不同小波函數對積分波動率估計的時序圖

從積分波動率不同估計方法比較可知（見圖1），4種小波函數估計的積分波動率時序圖與實際波動率時序圖差別均很小，變化趨勢一致，圖形基本吻合，其中IVd、IVl、IVc、IVh分別表示用Daubechies、Least Asymmetric、Coiflets、Haar小波函數對積分波動率的小波估計，RV為實際波動率。

以1分鐘交易數據為樣本，分別抽取5分鐘和10分鐘間隔數據作為新樣本L1和新樣本L2，其中5分鐘間隔抽樣規則為：從原始樣本第一個數據開始數，數到第5個作為L1的第一個數據，再往后數5個，即第10個數作為新樣本的第2個數據，并以此類推，得到新樣本L1。10分鐘間隔數據也采用同樣抽樣規則，得到新樣本L2。利用新樣本L1和L2計算實際波動率與積分波動率的小波估計，并以實際波動率與小波估計的相對誤差ξ=(IV-RV)/RV為研究指標，其中IV表示積分波動率的小波估計，則得到不同采樣頻率下的4種相對誤差。結果如表1所示。

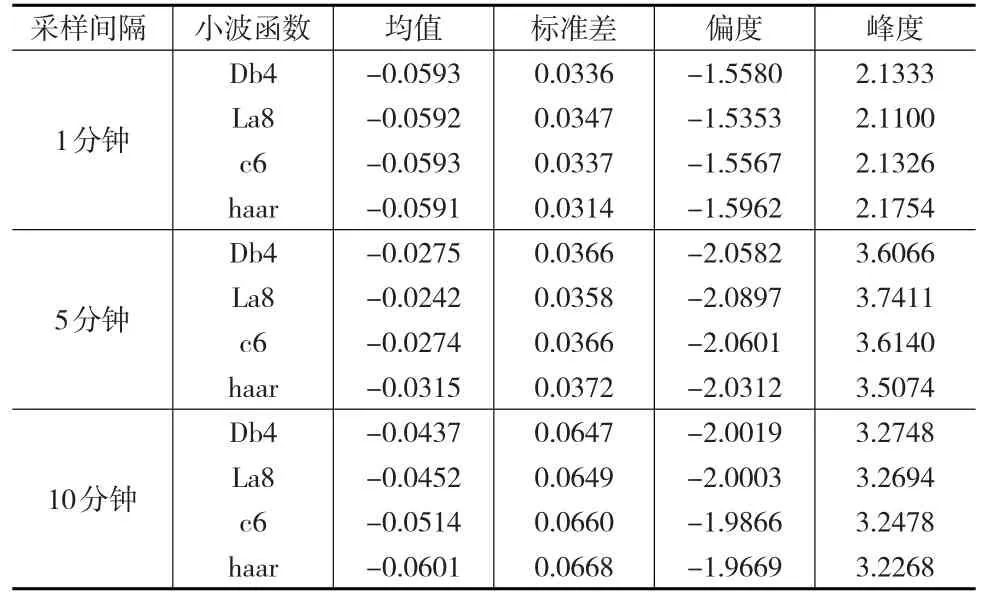
表1 不同小波函數下的相對誤差統計結果

由表1可知在相同抽樣頻率下，利用不同小波函數估計得到的相對誤差的各均值、標準差、偏度和峰度均比較接近，且都是左偏的，說明利用極大重疊離散小波變換估計積分波動率對所選用的小波函數不敏感，無論采用哪種小波函數，采樣間隔是1分鐘和5分鐘的相對誤差的標準差均明顯小于10分鐘采用間隔。特別地，對于5分鐘采樣間隔，相對誤差的均值絕對值最小。

從不同抽樣頻率各小波函數估計的相對誤差的直方圖可知，無論選取哪種小波函數及采樣頻率，實際波動率與積分波動率的小波估計的相對誤差均小于零，說明利用極大重疊離散小波變換方法估計積分波動率時比實際波動率要小，且從圖中可以看出5分鐘采樣頻率下相對誤差趨于零的天數明顯比1分鐘和10分鐘的多，即5分鐘采樣間隔下積分波動率小波估計與實際波動率最接近。從10分鐘相對誤差直方圖可以看出，相較于1分鐘和5分鐘，不同小波函數得到的估計值與實際波動率的誤差均變大，從尾部可以看出，極端值越來越多，說明有更大的誤差出現。

3 結論

高頻數據由于包含了更多的有效信息，能更加細膩地刻畫金融市場的細節，因而在對金融資產收益率的波動性進行研究時，金融高頻波動率有著低頻數據無法比擬的信息優勢。實際波動率作為金融高頻數據波動率的度量，無模型，計算相對簡便，而受到熱烈追捧。小波變換方法由于具有多分辨率特性，可以對信息成分采取逐漸精細的時域與頻域處理，被譽為“數學顯微鏡”，因而得到廣泛應用。本文首先用1分鐘高頻數據對波動率研究，得到實際波動率與基于極大重疊離散小波變換的積分波動率的小波估計時序圖基本吻合，然后對不同采樣間隔下的實際波動率與積分波動率小波估計進行比較分析，無論選取何種小波函數及抽樣頻率，小波估計均低于實際波動率。在頻率較高時，小波估計與實際波動率比較接近。特別在5分鐘采樣間隔下，小波估計與實際波動率最接近，說明5分鐘采樣頻率對波動率具有良好估計效果，且大部分學者均是基于5分鐘采樣間隔進行研究的[4,9,11]。同時在所選樣本中，也可以得到小波函數的選取對小波估計無明顯差異。

參考文獻：

[1]Andersen T G，Bollerslev T，Diebold F X，et al.The Distribution of Realized Stock Return Volatility[J].Financ Econ，2001b，(61).

[2]Barndorff-Nielsen O E，Shephard N.Power and Bipower Variation With Stochastic Volatility and Jumps[J].Journal of Financial Econo?metrics，2004，2(1).

[3]Lunde A，Hoeg E.Wavelet Estimation of Integrated Volatility[J].Com?puting in Economics&Finance，2003，33(2).

[4]秦喜文，劉文博，董小剛等.基于極大重疊離散小波變換的金融高頻數據波動率估計[J].吉林大學學報：理學版，2014，52(6).

[5]Percival D B，Walden A T.Wavelet Methods for Time Series Analysis[M].Cambridge:Cambridge University Press，2006.

[6]韓清，劉永剛.已實現波動率估計中不同降噪方法的比較分析及實證[J].數量經濟技術經濟研究，2009,(8).

[7]Daubechies I.Orthonormal Bases of Compactly Supported Wavelets[J].Communications on Pure and Applied Mathematics，1988，41(7).

[8]高靜.基于小波分析的高頻時間序列研究[D].天津:天津大學碩士論文,2007.

[9]蔡豐澤.基于小波分析的金融高頻數據波動率估計研究[D].長春：長春工業大學碩士論文,2016.

[10][美]Ruey S.Tsay.金融數據分析導論:基于R語言[M].北京：機械工業出版社,2013.

[11]劉文博.小波分析方法在高頻金融數據分析中的應用[D].長春：長春工業大學碩士論文,2010.