沃土為田 始得百花爭艷

徐光輝

“導學”是課堂教學的第一步，其重在導入，而意義卻在為“學”服務或是“學”本身。如何使一節課的開場讓學生耳目一新，迅速抓住學生的興趣點，同時緊密結合即將進行的研學給予學生啟示或是引發其對新知的關注和思考，為本節課的學習作好情感和知識上的準備，是“沈占立名師工作室”一直在研究的問題。

“妙語如珠”，暗藏深意

導學策略：巧妙設置導學語，在導學語中處處滲透新知識。

導入方式：聊天導入、故事導入、詩詞（歌曲）導入等。

啟示類型：概念的引入

例 《隨機事件》（人教版九年級數學上冊第二十五章第1節第一課時）

師：今天降溫了（結合當日天氣），大家要做好保暖。常說天有不測風云，是啊，月有陰晴圓缺，人有旦夕禍福；大千世界，精彩紛呈，有人守株待兔，有人甕中捉鱉。我們期待的結果，有時說曹操曹操到，有時卻是等到花兒也謝了。我們身邊常發生著各種各樣的事件，有些事件發生的結果可以預知，有些不可預知，這節課，我們就來研究一下這些有關“事件”的數學知識。

出示課題《隨機事件》

【設計意圖】導學語將本節課要學習的概念——隨機事件、必然事件、不可能事件都暗含其中。開頭的三個俗語：天有不測風云、人有旦夕禍福是隨機事件，月有陰晴圓缺是必然事件，形成初步印象。緊接著的兩個成語：“甕中捉鱉”代表了典型的必然事件；“守株待兔”在日常生活中被認為是一個不可能事件，數學角度解釋為可能性很小的隨機事件，正好可以作為研學環節中探究事件可能性大小的材料。最后用“說曹操曹操到”和“等到花兒也謝了”來表達必然事件和不可能事件帶給人們的主觀感受，引發情感參與。

【案例評析】此例使學生在聆聽導學語的過程中就領悟了各類事件的基本內涵，后續教學中，只需稍作引導便可明確三類事件的含義，概念的引入和教學變得輕松而自然。同時，成語和俗語充滿情趣，讓枯燥的概念課變得生動俏皮，容易引發學生的關注，達到知識導學和情感導學的目的。當概念教學完畢后，還能將這些材料作為概念辨析的素材，物盡其用，前后呼應。

“躬行實踐”，觀隅反三

導學策略：結合生活實踐，用實例或實驗操作讓學生感悟新知識。

導入方式：實驗操作導入、游戲導入、視頻導入等。

啟示類型：規律的探尋

例 《等式的性質》（人教版七年級數學上冊第三章第1節第二課時）

師：今天的數學課上我給大家帶來了一個新玩意兒，大家認識嗎？（指著天平）

生：天平。

師：你知道天平代表什么嗎？

生：公正、平等。

師：大家看現在天平兩邊放了重物，天平處于平衡的狀態，說明了什么？

生：兩邊的重量相等。

師：如果我們將天平的一端看作我們自己，另一端看作我們的對手，目前的狀態說明我和我的對手是平等的、旗鼓相當。可是，如果對方再努力一點點（老師向天平代表對手的一端放入一個很小的砝碼，天平失衡），天平就會向對方傾斜；如果對方倦怠或是退縮（老師從天平代表對手的一端取出一個砝碼，天平失衡），成功就會向我們靠近；如果我們倦怠或退縮了（老師從天平代表自己的一端取出一個同樣的砝碼，天平平衡），我們又回到了和對手同樣的位置。這就是“天平與人生”，天平中不僅包含著人生哲理，也包含著數學知識。等式就像平衡的天平，具有和天平同樣的性質。這節課，我們就來研究一下等式的性質。

出示課題：《等式的性質》

【設計意圖】此例導學部分采用天平實物操作，借助天平失衡又平衡的過程反復凸顯規律，學生在觀察實驗操作的過程中，已經感悟到“天平的兩邊同時增加或減少相同的重量，天平仍平衡”這一性質。在接下來的研學過程中，稍作引導，學生便可將天平的性質轉移到等式，得出等式的性質。

【案例評析】這個導學過程快速而精準，同時，語言中飽含的人生哲理而不顯突兀，體現了教學的藝術性，融合了學科教學和德育滲透，給予學生美好的情感體驗，展現了數學怡情之美。

“宣之使言”，引人入勝

導學策略：精心設置開放性探究，讓發散的途徑指向新知識。

導入方式：懸疑導入、探究性導入、舊知拓展等。

啟示類型：定理的生成

例 《垂徑定理》（人教版九年級數學上冊第二十四章第1節第二課時）

知識回顧：圓是中心對稱圖形，對稱中心即圓心；圓也是軸對稱圖形，它有無數條對稱軸，過圓心的直線就圓的對稱軸。（強調圓心地位）

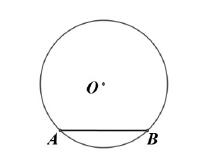
如圖：在⊙O中任取一弦AB。

鋪墊性設疑：這一圓一弦組成的圖形還是中心對稱圖形嗎？（不是）；是軸對稱圖形嗎？（是）。有幾條對稱軸？（1條）。探究導學：怎樣作出這條對稱軸？

【設計意圖】學生最有可能會考慮到兩種方法：1.過圓心O作弦AB的垂線；2.取弦中點M，作直線OM；其他可能考慮到的方法還有：取弧中點，作弧中點和圓心兩點所在的直線、作兩弧中點所在的直線、過弧中點作弦的垂線等。

方法1和方法2剛好對應垂徑定理及其推論。過圓心保證了這條直線是圓的對稱軸，同時引出等腰三角形△OAB，作垂線和取弦中點都可以聯系到等腰三角形的“三線合一”，得證其為弦的垂直平分線，結合過圓心便證明了這條直線是整個圖形的對稱軸了，垂徑定理的模型就此生成，結論也就呼之欲出了。

同時，方法1可歸結為過點作已知直線的垂線，無論點（圓心）在弦上還是弦外，直線有且只有一條；方法2可歸結為兩點確定一條直線（圓心、弦中點），則必須保證不重合，由此解決了學生在掌握定理時的頑疾——推論中，被平分的弦為什么不能是直徑的問題：若弦是直徑，中點就是圓心，兩點變一點，無法確定這條直線。其他幾種方法，都是垂徑定理的推廣，目前教材將其作為刪減內容，但其均為正確的命題，正好可以根據學生探究的深度和廣度靈活處理。

【案例評析】此導學過程既展現了“開放”的不確定性，也保障了導學的集中指向性，開放性所發散的各個方向均為生成定理、探究定理的一部分，探究的結果將全面涵蓋垂徑定理及其推論的方方面面，學生的探究成果全部成為研學的素材。

到目前為止，這是沈占立老師工作室的教師們公認的導學垂徑定理這一內容的最好方式，對其他生成性定理的課型導學有很好的示范作用。

畢達哥拉斯說：“在數學的天地里，重要的不是我們知道什么，而是我們怎么知道什么。”導學環節就是教師輔助學生實現“怎么知道什么”的開端，它絕不是單純的導入，必須精練簡短而目標明確。今后的教學中，工作室仍將集眾人之智，全力探索。

（作者單位：武漢市光谷實驗中學）