基于阻力和EEDI的船舶主尺度要素多學科設計優化

蘇紹娟 介推 劉波

摘要：

為尋找高效節能船舶主尺度要素，以一艘多用途船作為研究對象，從多學科設計優化的角度入手，根據普魯哈斯卡假設和三因次換算方法將船舶阻力參數化，采用等效能效指數將船舶能效設計指數（energy efficiency design index， EEDI）參數化，使其均為船舶主尺度要素函數。選用合適的多學科設計優化模型，運用第二代非支配排序遺傳算法（second generation non-dominated sorting genetic algorithm， NSGA-II）得到優化的船舶主尺度要素。對原船進行船型變換，得到優化船。利用CFD進行數值模擬，驗證優化船的阻力性能和EEDI優于原船的阻力性能和EEDI，達到優化的目的。

關鍵詞：

船舶能效設計指數（EEDI）; 船舶主尺度; 多學科設計優化; 阻力

中圖分類號： U661.1;U662

文獻標志碼： A

Multidisciplinary optimization design on ship principal dimensions

based on resistance and EEDI

SU Shaojuan1， JIE Tui1， LIU Bo2

（1. Naval Architecture and Ocean Engineering College， Dalian Maritime University， Dalian 116026， Liaoning， China;

2. Marine Departmnet， Dalian Shipping College， Dalian 116000， Liaoning， China）

Abstract：

To find the principal dimensions of high efficiency and energy saving ships， a multi-purpose ship is studied. From the perspective of the multidisciplinary optimization design， the ship resistance is parameterized according to Prohaska hypothesis and the three-dimensional conversion method， and the energy efficiency design index （EEDI） is parameterized using the equivalent efficiency index， which makes them to be the ship principal dimension functions. An appropriate multidisciplinary optimization design model is chosen. The second generation non-dominated sorting genetic algorithm （NSGA-II） is used to get the optimal ship principal dimensions. The original ship is converted into an optimal ship. The numerical simulation by CFD verifies that the resistance performance and EEDI of the optimal ship are superior to those of the original ship， thus the optimization is achieved.

Key words：

energy efficiency design index （EEDI）; ship principal dimension; multidisciplinary optimization design; resistance

收稿日期： 2017-05-03

修回日期： 2017-11-22

基金項目： 國家自然科學基金（51609031）;中央高校基本科研業務費專項基金（3132016346，3132017018）;遼寧省教育廳科學研究一般項目（L2015067）

作者簡介：

蘇紹娟（1979—），女，遼寧葫蘆島人，副教授，博士，研究方向為數字化船舶設計制造，（E-mail）katie306@163.com

0 引 言

船舶主尺度要素優化是一個復雜的非線性優化問題，涉及的因素較多。長期以來，國內外專家學者對此做了大量的研究工作：金雁等[1]運用網格法和AHP將多目標轉化為單目標進行船型主尺度論證;張寶吉等[2]以最小阻力為目標采用遺傳算法進行船型優化設計;劉寅東等[3]應用AHP和1～9標度將定性分析與定量分析結合，解決船型優選排序問題;金雁等[4]采用蟻群算法進行船舶主尺度優化論證。上述研究有的考慮阻力等單一技術指標，有的考慮技術、經濟等多個指標，均能有效地選擇合理的船型主尺度要素，但很少從系統的角度考慮各指標間的內在聯系。劉蔚[5]將7 000 m載人潛水器分解為若干個子系統，結合不同的多學科設計優化方法對其進行優化，取得了不錯的成果。張恒等[6]基于船的水動力性能對船型進行了綜合優化，并開發了船體型線多學科設計優化平臺，實現了基于所需目標的船體型線自動優化過程。

本文以一艘多用途船作為研究對象，研究阻力性能和

船舶能效設計指數（energy efficiency design index， EEDI）及其相互作用關系，通過多學科設計優化設計理論，采用第二代非支配排序遺傳算法（second generation non-dominated sorting genetic algorithm， NSGA-II）對該船的船型要素值尋優，從而實現尋找高效節能船型的目的。

1 阻力參數化

根據三因次換算方法[7]，船模的總阻力因數為

Ctm=Cpvm+Cfm+Cwm=（1+k）Cfm+Cwm （1）

式中：1+k為形狀因子;Cpvm，Cfm和Cwm分別為船模的黏壓阻力因數、摩擦阻力因數和興波阻力因數。

按照普魯哈斯卡假設，通常弗勞德數Fr在0.1與0.2之間時，可近似認為Cwm與Fr的四次方呈線性關系，故將式（1）變換為

CtmCfm=1+k+bFr4Cfm （2）

k采用Granville提供的計算公式[8]計算：

k=-0.03+32.8C2b（Lpp/B）2B/T （3）

式中：Cb為方形系數;Lpp為垂線間長;B為型寬;T為設計吃水。

摩擦阻力因數用國際拖曳水池會議（ITTC）公式計算：

Cf=0.075（lg Re-2）2（4）

式中：雷諾數Re=vLwl/ν，其中v為航速，Lwl為水線間長，ν為水的運動黏性系數，取海水在20 ℃時的運動黏性系數。

在相同Fr的情況下，船模興波阻力因數Cwm等于實船興波阻力因數Cw，故實船總阻力因數為

Ct=（1+k）Cf+Cwm+ΔCf=

（1+k）（Cf-Cfm）+Ctm+ΔCf

（5）

ΔCf為粗糙度補貼因數，通常取0.4×10-3，也可用ITTC推薦的公式：

ΔCf=105ksLwl1/3-0.64×10-3 （6）

ks通常取1.5×10-4 m，因此實船總阻力為

Rt=ρv2SCt/2 （7）

式中：ρ為海水密度;S為濕面積。S由文獻[9]提供的減量法計算：

S=LwlBT1T+2B+2Lwl-4.31Cb-12/3 （8）

式中：為排水體積，m3。

采用Fluent模擬船模在0.436，0.581，0.872，0.945，1.017，1.090，1.163 m/s這7個航速下的運動狀態。船模與實船的縮尺比為1∶50，故對應的實船航速為6 kn， 8 kn， 12 kn， 13 kn， 14 kn， 15 kn， 16 kn，其中12 kn為設計航速。在流體流過整個流域的過程中，阻力監視器監測的阻力值變化不大;基本穩定后，取相鄰總阻力的平均值，所得船模數值見表1。

表1 船模數值

根據普魯哈斯卡假設，取Fr在0.1與0.2之間

圖1 擬合曲線

的摩擦阻力因數和總阻力因數，將Ctm/Cfm作為y軸坐標，

Fr4/Cfm作為x軸坐標作圖，擬合出的曲線見圖1。根

據式（2），可得k=0.211，b=

0.750 5。采用式（3）得到k=0.212，模擬誤差僅為0.47%，說明本文模擬出的數值正確。

這樣便把總阻力值與船型要素聯系起來，總阻力值可用垂線間長Lpp，水線間長Lwl，型寬B，吃水T，方形系數Cb等要素表示出來，實現了參數化[10]。

2 EEDI參數化

EEDI的概念[11-12]如式（9）所示：

IEEDI=cFcSFCPmDHv （9）

式中：cF為碳轉換因子;cSFC為燃油消耗率;mDH為載質量;P為總功率。

EEDI與船舶主機功率和副機功率有關，主機功率為在無風無浪條件下75%的額定功率，副機功率是個大約值。若式（9）中的P約等于航行狀態下的有效功率Pe，則等效能效指數[8-9]為

I′EEDI=cFcSFCPemDHvref （10）

式中：Pe=Rtv;vref為船舶航行狀態下的航速。

mDH=Δ-m0

m0=（mh+mf+mm）（1+k′）

mh=chL1.657B0.777D0.282 5T0.045 7Cb0.014 56

mf=cfΔ

mm=cmPB（11）

式中：Δ為排水量;m0為空船質量;mh為鋼料質量;mf為舾裝質量;mm為機電設備質量;ch為鋼料因數，取值為0.038 9;cf為木作舾裝因數，取值為0.023 1;cm為機電質量因數，取值為0.112;k′為儲備浮力因數，取值為0.045;L為船長;D為型深;PB為主機額定功率。

該船的主機使用的是MAN B&W 8L27/38，額定功率為2 640 kW，臺數為3，使用重油航行，cF=3.114 4，cSFC=185 g/（kW·h）;副機的cSFC=205 g/（kW·h）;未使用軸帶發電機與創新節能技術。

綜上，該船的等效能效指數也可以用船型要素表示，同樣實現了參數化。

3 多學科設計優化

3.1 多學科設計優化理論

多學科設計優化是一種設計優化的方法論，它最早是由美籍波蘭人J Sobieszczanski-Sobieski提出的，隨后NASA的Langley研究中心對多學科設計優化給出了定義：多學科設計優化是一種利用系統中相互作用的協同機制來設計復雜工程系統和子系統的方法論。它的主要思想就是通過分解、協調等手段將復雜工程系統分解為與現有工程設計組織形式相一致的若干子系統，從而利用現有的各學科分析設計工具及合適的優化策略，對復雜工程系統進行綜合設計，實現復雜產品的功能需求，以達到縮短設計周期、降低開發成本、提高產品競爭力的目的。[13]

3.2 多學科設計優化方法

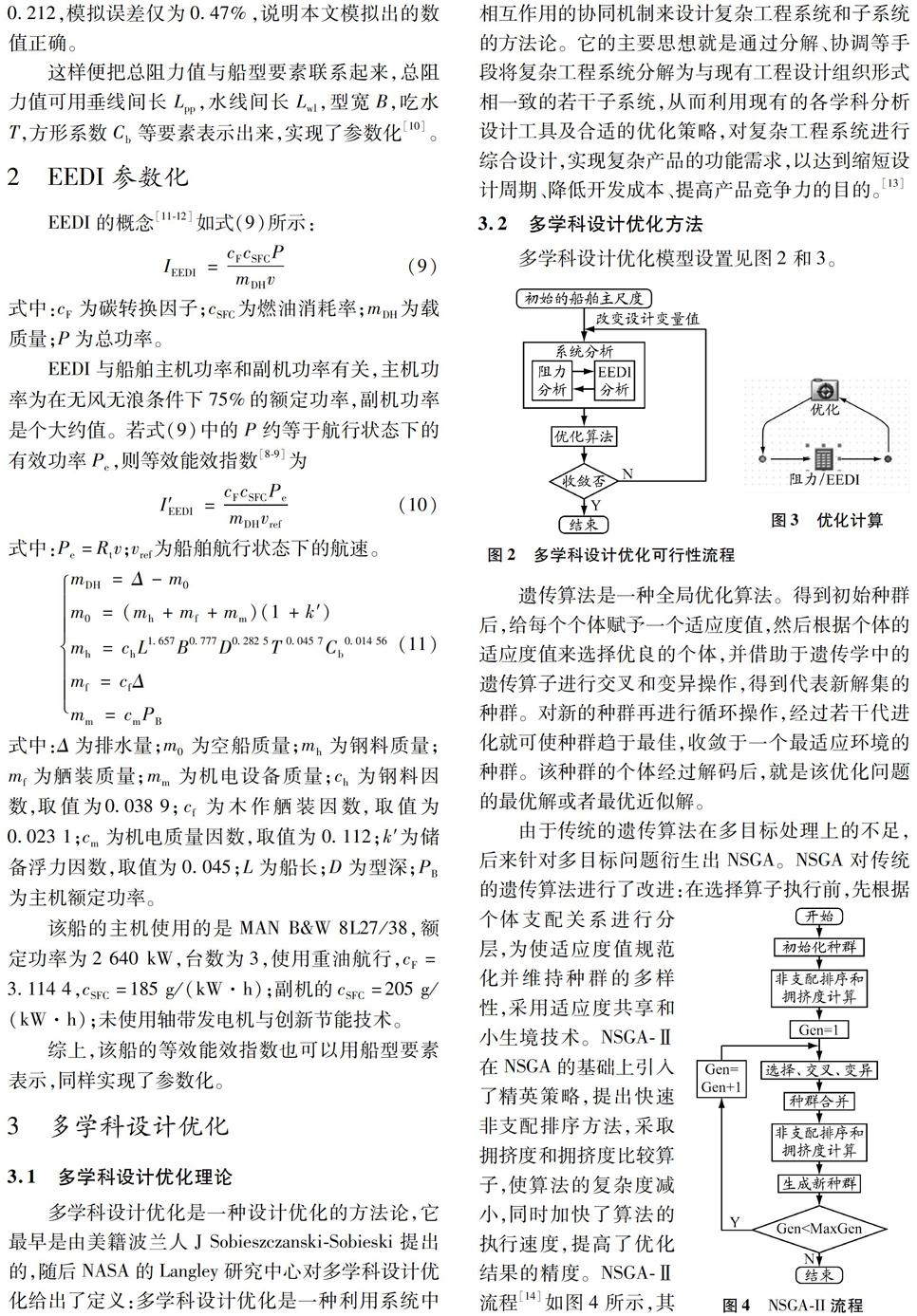
多學科設計優化模型設置見圖2和3。

遺傳算法是一種全局優化算法。得到初始種群后，給每個個體賦予一個適應度值，然后根據個體的適應度值來選擇

優良的個體，并借助于遺傳學中的遺傳算子進行交叉和變異操作，得到代表新解集的種群。對新的種群再進行循環操作，經過若干代進化就可使種群趨于最佳，收斂于一個最適應環境的種群。該種群的個體經過解碼后，就是該優化問題的最優解或者最優近似解。

由于傳統的遺傳算法在多目標處理上的不足，后來針對多目標問題衍生出NSGA。NSGA對傳統的遺傳算法進行了改進：在選擇算子執行前，先根據

圖4 NSGA-II流程

個體支配關系進行分層，為使適應度值規范化并維持種群的多樣性，采用適應度共享和小生境技術。NSGA-Ⅱ在NSGA的基礎上引入了精英策略，提出快速非支配排序方法，采取擁擠度和擁擠度比較算子，使算法的復雜度減小，同時加快了算法的執行速度，提高了優化結果的精度。NSGA-Ⅱ流程[14]如圖4所示，其中：Gen為迭代次數，MaxGen為最大迭代次數。

3.3 優化過程和優化結果

優化目標：在設計航速下，Rt最小和I′EEDI最小。

設計變量：主要是主尺度要素變量Lpp，Lwl，B，T和Cb。該船屬于多用途船，對甲板上的布置有一定的要求，故要保證其型寬B（37.2 m）不變，而其他要素在設計值左右變化，具體取值范圍見表2。

表2 設計變量的取值范圍及優化結果

約束條件：除了設計變量的約束外，排水量

（31 496.9 t）、設計航速（12 kn）、海水密度、水的運動黏度系數、重力加速度、碳轉換因子和燃油消耗率是不變的。

采用NSGA-II，種群規模為20，進化代數為30，交叉概率為0.9，交叉分布指數為10，變異分布指數為20。經過600次的迭代優化計算，整個優化過程如圖5所示，圈起來的點即為最優解。選取這個最優解方案，優化結果見表2。原船與優化船的其他主尺度要素對比見表3。

圖5 優化過程

表3 原船與優化船的其他主尺度要素對比

3.4 優化后的船型阻力及EEDI結果分析

根據式（1）～（8）可得到原船和優化船在相應航速下的總阻力因數和總阻力值，根據式（10）和（11）可得到各航速下優化船的EEDI，見表4。

從表4可以看出，優化船的阻力性能和EEDI

表4 原船與優化船的總阻力和EEDI比較

優于原船的阻力性能和EEDI，優化的目的已經達到。在航速偏低的情況下，原船與優化船的總阻力和EEDI幾乎一致;在設計航速為12 kn時，船舶減阻9.29%，節能6.66%;隨著航速的增加，減阻效果越發明顯，節能效果無明顯變化規律，這主要是由于影響EEDI的因素很多。

4 CFD數值模擬驗證

采用Fluent對船型進行數值模擬。

圖6～9為原船與優化船在航速為12 kn時的速度和動壓力云圖以及流線圖對比。圖6中，兩船首部自由液面的速度云圖雖然差別不很明顯，但仍能看出原船首肩處的速度大于優化船的，這可能是因為進流段曲率過大而使肩波處受到不利干擾，興波阻力增大，而優化船有效緩解了這一點。從圖7可以明顯看出，原船自由液面的速度波動更劇烈，這從側面說明優化船的興波阻力性能優于原船的。從圖8可以看出，原船首尾的壓差明顯大于優化船的，這也說明原船的黏壓阻力大于優化船的。從圖9可以看出，優化船的船尾流線比原船的更加光滑、流暢，并且流線更向中部集中，適當緩解了艉部流線的分離現象[15]。這些云圖、流線圖均能在一定程度上反映優化船的阻力性能優于原船的。

圖6 航速為12 kn時原船（左）和優化船（右）首部自由

液面速度云圖

圖7 航速為12 kn時原船（左）和優化船（右）自由液面

速度云圖

圖8 航速為12 kn時原船（左）和優化船（右）動壓力云圖

圖9 航速為12 kn時原船（左）和優化船（右）船尾流線圖

表5為原船與優化船的摩擦阻力、黏壓阻力和興波阻力的對比。從表5看出：主要是黏壓阻力和興波阻力的減小致使優化船總阻力小于原船總阻力;優化船的摩擦阻力大于原船的，這主要是因為優化船的長度增加且濕面積較大，但摩擦阻力增量較小。雖然優化船船長增加導致摩擦阻力增加，但相應的進流段和去流段的加長使艏艉曲率變小，緩解了艏艉可能出現的舭渦，進而使黏壓阻力減少;船長的增加使得整艘船更加“瘦削”，這也有利于興波阻力的減少。

表5 原船與優化船阻力比較

參數化的優化過程雖然只提供了一個尋優的依據，但也間接反映了各船型要素與阻力間的關系。結合圖10，在本文設置的垂線間長、水線間長、吃水和方形系數的范圍內，在排水量和型寬不變的情況下，總體分析船型要素對總阻力的影響。

c）方形系數

圖10 船型要素與總阻力的關系

垂線間長的增加會導致總阻力的減小。垂線間長的增加必然會導致船長增加，雷諾數增加，摩擦阻力因數減小，濕面積增大，但總體摩擦阻力的增加是相對微小的，而且船長的增加相當于長寬比增加了，“瘦削”的船型會使黏壓阻力和興波阻力下降，且其下降值大于摩擦阻力的上升值，故總阻力下降。然而，在航速很低時，興波阻力過小，甚至模擬結果為負值，船長的增加可能會導致總阻力增加。

吃水減小會導致總阻力減小。原船的吃水已經為6.2 m，為保證排水量不變，縮小的空間并不大，而且吃水的減小會在一定程度上減少濕面積，減小摩擦阻力。然而，吃水的選擇通常不依據阻力性能，而從布置、穩性、航道和港口水深限制等方面考慮（若船舶吃水減小則航道和港口對其的限制就會減弱）。該船是肥大船且兼有打撈運輸的功能，稍微減小其吃水就能對阻力有一定的改善且又滿足了各航道的要求。

方形系數減小會導致總阻力減小。方形系數是表示船體水下部分肥瘦的一個重要標準。在排水量不變的情況下，減小方形系數，相當于讓船變“瘦”，黏壓阻力和興波阻力會明顯減小，但鑒于排水量、艙容、布置等的要求，方形系數不能過小。

5 結 論

本文闡述了多學科設計優化的技術理論，并且介紹了多學科設計優化的流程，對阻力和EEDI進行參數化分析后使用多學科設計優化算法對船型要素進行尋優，得到了優化的船型要素值。最后通過對原船進行船型變換，得到優化船。通過數值模擬，驗證了優化船的阻力性能和EEDI確實優于原船的，達到了優化的目的。

由于軟、硬件條件限制影響了CFD的計算精度，下一步的工作應進一步加強網格的劃分，合理劃分疏密有致的結構網格和非結構網格，流域的劃分應再精簡、分塊，這樣既能減少網格又能提高網格質量，有效提高模擬計算的精度。

在對EEDI的分析中，取主副機功率近似等于有效功率，因為減小阻力和降低能效指數的本質是相同的，所以結果分析著重于阻力性能分析。阻力性能的提高和推進效率的提高勢必會帶來主機功率的下降和EEDI的下降。

本文中原船的載質量為20 500 t，優化后載質量為20 190 t，載質量變小對船舶的經濟性能有一定的不良影響。在接下來的工作中要考慮更多的指標，從技術、經濟、環境等多方面對船型進行優化論證。

參考文獻：

[1]金雁， 王麗錚， 陳順懷. 川江及三峽庫區變吃水干散貨船的優化論證[J]. 船海工程， 2006（6）： 44-47.

[2]張寶吉， 馬坤， 紀卓尚. 基于遺傳算法的最小阻力船型優化設計[J]. 船舶力學， 2011， 15（4）： 325-331.

[3]劉寅東， 唐煥文， 李紀選. 船型多方案選優決策的層次分析方法[J]. 船舶工程， 1996（1）： 22-25.

[4]金雁， 趙耀. 基于改進蟻群算法的船舶主尺度優化[J]. 華中科技大學學報（自然科學版）， 2008， 36（11）： 99-102.

[5]劉蔚. 多學科設計優化方法在7 000米載人潛水器總體設計中的應用[D]. 上海： 上海交通大學， 2007.

[6]張恒， 詹成勝， 劉祖源， 等. 基于船舶阻力性能的船型主尺度參數敏感度分析[J]. 船舶工程， 2015， 37（6）： 11-14.

[7]姜次平. 船舶阻力的三因次換算方法[J]. 船舶工程， 1981（1）： 7-11.

[8]宋家瑾， 周占群， 謝克振. 對肥大船估算形狀因子實用方法的探討[J]. 交通部上海船舶運輸科學研究所學報， 1981， 1（1）： 81-91.

[9]曾祥華， 王介文. 減量法求船舶濕面積[J]. 武漢造船， 1997， 3（1）： 19-23.

[10]LI Dongqin， WILSONP A， ZHAO Xin. Establishment of effective metamodels for seakeeping performance in multidisciplinary ship design optimization[J]. Journal of Marine Science and Technology， 2016， 24（2）： 233-243.

[11]劉繼龍. 船舶能效設計指數分析[D]. 大連： 大連海事大學， 2013.

[12]LIU Shukui， SHANG Baoguo， PAPANIKOLAOU A， et al. Improved formula for estimating added resistance of ships in engineering application[J]. Journal of Marine Science and Application， 2016（4）： 442-451

[13]張利. NSGA2算法及其在電力系統穩定器參數優化中的應用[D]. 成都： 西南交通大學， 2013.

[14]倪崇本. 基于CFD的船舶阻力性能綜合研究[D]. 上海： 上海交通大學， 2012.

[15]劉英良. 基于CFD的超大型集裝箱船線型優化研究[D]. 北京： 中國艦船研究院， 2014.