MMC在船舶中壓直流電力系統中的應用

郭燚 張震 雷玉磊

摘要：

在船舶中壓直流（medium voltage direct current， MVDC）電力系統中，為解決功率為36 MW的發電機電壓的整流問題，建立適用于船舶MVDC電力系統的模塊化多電平換流器（modular multilevel converter，MMC）模型。在空間矢量控制方法的基礎上，加入橋臂電壓控制。在直流電壓為5 kV及負載不同的情況下，應用MATLAB/Simulink對該模型進行仿真，驗證模型和控制方法的有效性。基于此，研究該模型在不同直流電壓（5～30 kV）等級下的性能表現。仿真結果表明：在36 MW/5 kV的額定工況下MMC存在效率低的問題;直流電壓等級對MMC輸出直流電壓的紋波影響不大，但對MMC的效率有明顯的影響。

關鍵詞：

模塊化多電平換流器（MMC）; 中壓直流（MVDC）; 直流電壓等級; 損耗

中圖分類號： U665.12

文獻標志碼： A

Application of MMC in ship MVDC power system

GUO Yi， ZHANG Zhen， LEI Yulei

（

Logistics Engineering College， Shanghai Maritime University， Shanghai 201306， China）

Abstract：

In order to solve the voltage rectification problem of generators with the power of 36 MW in the ship medium voltage direct current （MVDC） power system， a modular multilevel converter （MMC） model is established for ship MVDC power system. On the basis of the space vector control method， the bridge arm voltage control is joined. The model is simulated by MATLAB/Simulink in the condition of 5 kV DC voltage and the different loads so as to validate the effectiveness of the model and the control method. Based on the above， the performance of the model in different DC voltage （between 5 kV and 30 kV） grades is studied. The simulation results show that： the efficiency of MMC is lower under the rated condition of 36 MW/5 kV; the DC voltage grade has slight influence on the DC voltage ripple output by MMC， but has significant influence on the efficiency of MMC.

Key words：

modular multilevel converter （MMC）; medium voltage direct current （MVDC）; DC voltage grade; loss

收稿日期： 2017-03-24

修回日期： 2017-05-23

作者簡介：

郭燚（1971—），男，安徽安慶人，副教授，博士，研究方向為電力電子與電力傳動，（E-mail）gymwmw@live.cn

0 引 言

隨著現代艦船對能量需求的不斷提升，船舶電網從中壓交流系統向中壓直流（medium voltage direct current， MVDC）系統轉變[1-4]。文獻[5]率先提出了具有高可靠性和良好供電連續性的環形電網。文獻[6]和[7]在此基礎上提出了新型環形船舶MVDC電力系統模型，以2臺36 MW的主發電機和2臺4 MW的輔助發電機作為電源，每臺發電機均經過整流器整流后輸出5 kV的直流電壓，為環形直流母線供電，并采用分區供電，使船舶MVDC電力系統即使在惡劣的工況下也能保持極佳的性能。該模型如圖1 所示，為了研究方便，省去了輔助發電機部分。

圖1

簡化后的環形船舶MVDC電力系統模型

圖1中，發電機發出的交流電，由整流器進行整流后變成直流電送入環形直流電網，直流電網為常規負載、雷達、脈沖負載、推進電機等供電。在該模型中，如何設計適合的整流器成為研究熱點。[8-9]文獻[7]中，整流部分采用橋式二極管整流器，而在實際工況下一般不使用二極管的整流方式。目前第三代直流輸電系統中常用的整流器主要有3種，即三相半橋換流器、二極管箝位型換流器和模塊化多電平換流器（modular multilevel converter， MMC）。

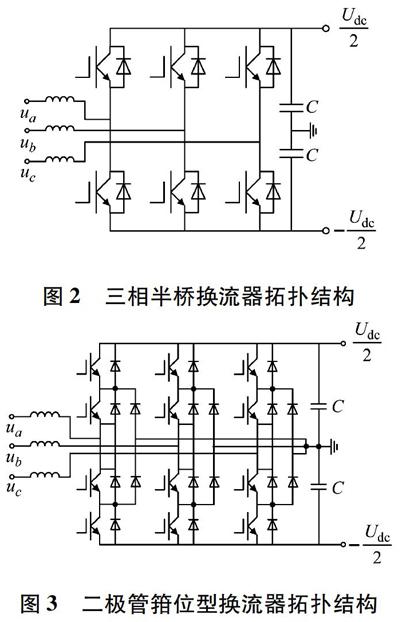
圖2是三相半橋換流器的拓撲結構（uj，j=a，b，c，為j相交流電壓;Udc為直流側電壓;C為電容），由6個橋臂組成，在高壓、大功率的情況下，往往需要多個IGBT并聯或串聯以提高換流器的容量和電壓等級。圖3所示的二極管箝位型換流器能夠產生3個電平，比三相半橋換流器更能改善諧波質量，代價是需要更多的電力電子器件。這兩種換流器都需要在直流側并聯大容量電容，并且均使用脈沖寬度調制（pulse width modulation，PWM）技術進行調制。與這2種換流器相比，MMC因具有制造難度低、損耗低、階躍電壓低、波形質量好以及故障處理能力強的優點[10]而被廣泛應用于直流輸電系統。目前已經有一些學者[2，8-9]開始研究使用MMC對船舶發電機進行整流，并且取得了不錯的成果，但在已有的研究成果中，MMC的功率均小于6 MW，很難直接應用于圖1所示的船舶MVDC電力系統中。

本文針對圖1所示的船舶MVDC電力系統，搭建功率為36 MW的MMC-MVDC仿真模型，通過仿真驗證該模型的可行性。提出MMC損耗

估算公式，進一步研究MMC-MVDC模型在不同的直流電壓等級下的性能，并驗證估算公式的有效性。

圖2

三相半橋換流器拓撲結構

圖3

二極管箝位型換流器拓撲結構

1 MMC-MVDC模型設計

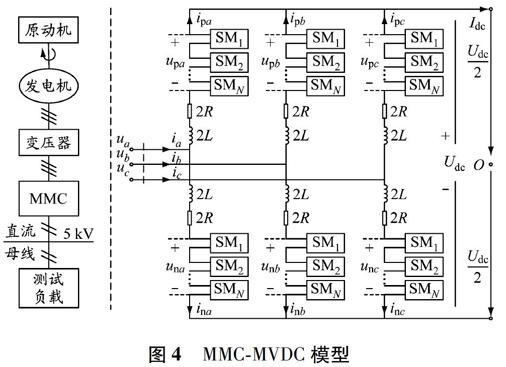
在圖1所示的模型中，原動機、發電機和整流器共同組成了直流電網的發電系統。使用MMC作為整流器，并且引入變壓器進行電氣隔離，設計出MMC-MVDC模型，見圖4。

圖4

MMC-MVDC模型

在圖4中，左側是模型框圖：原動機提供原始動力，帶動發電機發出三相交流電;在發電機與MMC之間加入變壓器，使發電機在額定電壓下工作，并保證MMC交流側的電壓保持在最佳狀態，同時將發電機與船舶電網部分進行電氣隔離，使系統更加安全可靠。MMC采用如圖4右側所示的三相結構[11]，其中：O點表示零電位點;三相MMC包含6個橋臂，每個橋臂由N個子模塊（SM）串聯而成;同一相上、下兩個橋臂（用p和n區分）之間引入2個電感值為2L的限流電感，對子模塊的充放電電流進行限制，同時也能限制相間環流;帶不同下標的i和u分別表示某一相或某一相上、下橋臂的電流和電壓;Idc為總直流電流;2R為電阻值。采用這種經典結構控制方便，性能穩定。

2 MMC模型設計

2.1 MMC主電路設計

MMC主電路的設計主要包括交流側電壓計算、子模塊拓撲選擇、單橋臂子模塊數量確定，以及子模塊電容和橋臂電感參數的選擇計算，其中最重要的是子模塊電容和橋臂電感參數的選擇計算，它們直接影響MMC的可控性和工作性能。

為使MMC具備向交流系統發出無功功率的能力，文獻[12]認為MMC交流側相電壓峰值應小于直流母線電壓的一半，即選取

Uv<Udc/2

（1）

在MMC-MVDC模型中，發電機輸出的三相交流電的相電壓峰值為4 100 V， 頻率為240 Hz，因此可選擇變壓器的變比為4 100∶2 250，使得MMC交流側相電壓峰值Uv=2 250 V。

傳統的MMC的子模塊主要分為半橋型和全橋型兩類（見圖5，其中T1，T2，T3和T4為開關器件）。

圖5

半橋型子模塊和全橋型子模塊

全橋型子模塊結構復雜，控制策略多，在系統發生故障時能夠實現閉鎖，具有故障穿越的能力[13];半橋型子模塊結構簡單，控制方便，并且成本低，但是在系統發生故障時不能實現完全閉鎖。本文暫時不考慮系統出現故障時的情況，因而選擇半橋型子模塊進行建模。

MMC用于整流時，在使用載波相移技術進行調制時，一般N取值為4～10，在使用最近電平逼近調制（nearnest level modulation， NLM）方式時，N取值越大效果越好，例如Trans Bay Cable HVDC工程的N=216[14]，上海南匯風電場MMC-HVDC示范工程的N=48[15]。NLM方法簡單，耗費控制器資源少，特別對于船上頻率為240 Hz的高頻發電機，這種調制方式能夠明顯減小開關頻率，因此本文選擇NLM方式進行調制。參考文獻[16]，設置N=20。

在高壓直流輸電系統中，常使用以下的公式計算子模塊電容和橋臂電感參數[12，17]：

C0=Ps3kNωεUC2

1-kcos φ2232

（2）

L0=18ω20C0UC

Ps3Ikm+Udc

（3）

對于MMC-MVDC模型，取MMC功率Ps=36 MW，電壓調制比k=0.9，單橋臂子模塊數N=20，交流電源角速度ω=1 508 rad/s，子模塊電容電壓UC=250 V，功率因數cos φ=1，電容電壓波動百分比ε=5%和二倍頻環流峰值Ikm=1.2 kA，計算得出電容和電感的參考值分別為C0=0.1 F和L0=32.7 mH。然后，開環運行MMC，k固定在0.9，將電容和電感在計算出的參考值附近進行微調，直到MMC的輸出直流電壓為5 kV為止。這樣能夠保證MMC在穩態工作時k穩定在0.9左右。經過仿真調試，最終確定C0=0.13 F， L0=2L=28.5 mH。

由式（2）和（3）不難分析出，相比于高壓電力系統，中壓電力系統電壓低、電流大，設計MMC時就需要更大的電容和更小的電感才能使其工作在最佳狀態。

2.2 MMC控制策略設計

控制系統對MMC整流的實現至關重要。對MMC這類電壓源型換流器控制方法的研究一直在進行，早期通常采用間接電流控制，方法簡單，無須電流反饋控制，實現方便，但是存在電流響應慢的缺點。隨著現代電力電子技術的飛速發展，直接電流控制應運而生。該控制方法以快速的直接電流反饋為特征對電流進行直接控制，能夠獲得高品質的電流響應，已成為發展的主流[18]。在直接電流控制技術中，矢量控制技術應用最為廣泛，該技術將變換

器在abc坐標系下的數學模型轉換為dq坐標系下的數學模型，將電流電壓等三相交流量轉換成兩相直流量，引入前饋量進行解耦，簡化了數學模型，適

合于MMC的控制。

對于圖4中的三相MMC拓撲結構，由文獻[19]得到dq坐標系下MMC基本單元的頻域數學模型：

（R+sL）id（s）=ud（s）-vd（s）+ωLiq（s）

（R+sL）iq（s）=uq（s）-vq（s）-ωLid（s）

根據上述頻域數學模型，

以id和iq為狀態變量，以ud和uq為擾動分量，以vd和vq（MMC輸出的電壓分量）為輸入變量，引入電壓耦合補償項ωLid和ωLiq，采用PI控制器，得到電流控制器數學模型：

vd=ud+ωLiq-kp1（i*d-id）-ki1∫（i*d-id）dt

vq=uq+ωLid-kp2（i*q-iq）-ki2∫（i*q-iq）dt

式中：i*d和i*q為電流參考值;kpj和kij（j=1，2）分別是PI控制器的比例系數和積分系數。

根據上式設計內環電流控制器，以電壓控制和無功功率控制為外環控制器，同時增加橋臂電壓控制，設計出如圖6所示的MMC控制器。

圖6

MMC控制器

圖6所示的MMC控制器，由矢量控制與橋

臂電壓控制結合而成，pjC和njC分別是j相上橋臂和下橋臂子模塊電容電壓的平均值。外環是電壓環和無功功率環，內環是電流環，控制器的輸入為Udc和無功功率Q，Udc參考值U*dc設為5 kV。MMC對Q進行控制，能夠起到動態補償交流側Q的作用[20]，為簡化研究，將Q參考值Q*設為零。輸出三相虛擬電動勢ej （j=a， b， c）。在此基礎上，將ej加上一個修正量，實現對橋臂電壓的控制。最終控制器輸出MMC三相調制電壓ej_ref （j=a， b， c），結合NLM算法和電容電壓均衡策略最終對MMC進行控制。控制器直接對電流進行控制，因而能夠獲得高品質的電流響應。

3 MMC-MVDC仿真建模和分析

在對MMC主電路以及控制策略分析的基礎上，建立如圖7所示的MMC-MVDC仿真模型，包括原動機模型[21]、發電機模型[22]、變壓器模型、MMC模型和測試負載。圖7中：P1為系統有功功率;P、N為直流電壓輸入端口;P為功率計算模塊計算出的

圖7

MMC-MVDC仿真模型

有功功率。

發電機額定功率36 MW，相電壓峰值4.1 kV，頻率240 Hz;變壓器變比4 100∶2 250，額定轉速3 600 r/min;MMC模型采用上一節計算的參數。建模的具體參數見表1。

表1

MMC-MVDC建模參數

3.1 MMC對發電機影響仿真分析

為研究MMC對交流側發電機的影響，將測試負載設置為36 MW的感性負載，使系統工作在額定功率下，仿真結果見圖8。

a）直流側電壓

b）交流側電壓

c）交流側電流

圖8

額定功率運行時MMC電壓

電流波形

圖8a）是MMC直流側電壓波形，從圖中可以看出，穩態時直流電壓在5 kV上下波動，且紋波因數僅為0.5%，完全滿足直流電網的要求。圖8b）和8c）是MMC交流側電壓和電流波形，諧波失真（THD）率分別是0.13%和0.14%，基本沒有波形畸變，這表明MMC對交流側發電機的負面影響很小。

3.2 MMC-MVDC模型在不同負載下仿真分析

為進一步驗證所搭建模型的動態特性和穩態特

性，對MMC-MVDC模型在不同負載下的性能表現進行仿真分析。開始時，系統連接功率為9 MW的阻性負載啟動;在0.1 s時，負載突變為18 MW的感性負載;在0.2 s時，滿載運行，負載為36 MW的感性負載。仿真結果見圖9。

a）交流側電壓

b）交流側電流

c）直流側電壓

d）直流側電流

e）MMC輸入、輸出有功功率

圖9

MMC-MVDC電壓、電流、功率仿真波形

圖9a）是交流側輸入的三相電壓波形，由圖可知MMC對發電機發出的交流電壓基本無影響。圖

9b）顯示，交流側三相電流隨著負載功率的增加而增大。圖9c）是直流側的電壓波形，可以看到：直流電壓達到穩態時穩定在5 000 V;隨著負載增加，紋波電壓略有增大，但是均保持在±12.5 V之內;在0.1 s負載突變時，直流電壓波動小于80 V;在0.2 s時，電壓波動小于150 V，滿足船舶MVDC電力系統母線電壓4 500～5 500 V的限制[6]。圖9d）是直流側的電流波形。實驗結果表明，MMC-MVDC仿真模型無論是動態特性還是穩態特性均滿足船舶MVDC電力系統的要求。圖9e）是交流側輸入的有功功率和直流側輸出的有功功率，經計算，在前0.2 s，MMC的效率在98%以上，但是當系統滿載運行時，效率卻降到了93%，MMC的損耗率高達7%，在高壓系統中這一損耗率僅為1%[13]，可見在36 MW和5 kV的工況下，雖然MMC的電壓電流和動態響應均能滿足電網要求，但是存在效率過低的問題。

3.3 MMC損耗分析

為對MMC的損耗進行分析，用下式進行損耗估算：

Ploss=3N（λIrms）2RIGBT+NIout2RIGBT

（4）

式中：Irms是交流側電流的有效值;λ是損耗因數，與MMC的控制策略有關，經試驗研究，MMC-MVDC模型中λ=0.592。在36 MW和5 kV的工況下，N=20，RIGBT=0.001 Ω，Irms=8.49 kA，Iout=7.20 kA，因此Ploss=2.52 MW。在仿真試驗中，實際損耗為2.55 MW，與計算結果基本相等。

從式（4）可以看出，MMC的效率受流經MMC電流的影響。為驗證猜想的正確性，接下來研究在不同直流電壓等級下MMC-MVDC模型的性能。

4 不同直流電壓等級下MMC-MVDC模型的性能

針對船舶MVDC電力系統母線電壓的要求，文獻[5]中給出1～35 kV的7個電壓等級。本文選取5， 6， 12， 18， 24， 30 kV等6個電壓等級進行仿真驗證，仿真結果見表2，MMC的效率見圖10。

表2

不同直流電壓等級下MMC-MVDC模型的特性

由表2可以看出，在不同直流電壓等級下，MMC的輸出直流電壓紋波因數均小于1%，說明直流側電壓的高低對紋波影響較小。隨著電壓等級的升高，需要調節變壓器的變比，使得MMC交流側電壓滿足式（1）的要求。同時，隨著MMC交流側電壓的升高，交流側電流降低，并且MMC的效率顯著提高，當直流側電壓大于18 kV后，MMC效率達到99%以上。

圖10

不同直流電壓等級下MMC效率

圖10是在不同直流電壓等級下，根據式（4）計算得到的MMC效率和通過仿真得到的MMC效率曲線圖。兩條曲線基本吻合，證明式（4）能夠對MMC的損耗進行合理估算。同時可以看到，MMC效率隨著直流電壓的升高而升高，容易得到MMC

的損耗與流經MMC的電流的平方成正比。

5 結束語

針對船舶中壓直流（MVDC）電力系統，設計了功率為36 MW的MMC-MVDC模型，提出了空間矢量控制與橋臂電壓控制相結合的控制策略。通過MATLAB進行仿真，驗證了模型和控制算法的有效性。提出了MMC的損耗估算公式，研究了模型在不同直流電壓等級下的性能，結果表明估算公式的誤差不超過1%。進一步的研究方向為：（1）在MMC子模塊最大功率受限的情況下，設計出適合大功率船舶MVDC電力系統的MMC模型;（2）在直流電壓等級較低的情況下，提高MMC的效率。

參考文獻：

[1]

SU Chun-lien， LIN Kun-liang， CHEN Ching-jin. Power flow and generator-converter schemes studies in ship MVDC distribution systems[J]. IEEE Transactions on Industry Applications， 2016， 52（1）： 50-59. DOI： 10.1109/TIA.2015.2463795.

[2]VECHALAPU K， BHATTACHARYA S. Modular multilevel converter based medium voltage DC amplifier for ship board power system[C]//International Symposium on Power Electronics for Distributed Generation Systems. IEEE， 2015： 1-8. DOI： 10.1109/PEDG.2015.7223098.

[3]THONGAM J S， TARBOUCHI M， OKOU A F， et al. All-electric ships - a review of the present state of the art[J]. IEEE Conference Publications， 2013： 1-8. DOI： 10.1109/EVER.2013.6521626.

[4]MO Ran， LI Rui， LI Hui. Isolated modular multilevel （IMM） DC/DC converter with energy storage and active filter function for shipboard MVDC system applications[C]//Electric Ship Technologies Symposium （ESTS）. IEEE， 2015： 113-117. DOI： 10.1109/ESTS.2015.7157871.

[5]IEEE Industry Applications Society. IEEE recommended practice for 1 kV to 35 kV medium-voltage DC power systems on ships[S]. IEEE Standards Association， 2010： 1-54. DOI： 10.1109/IEEESTD.2010.5623440.

[6]ALI H， DOUGAL R， OUROUA A， et al. Cross-platform validation of notional baseline architecture models of naval electric ship power systems[C]//Electric Ship Technologies Symposium. IEEE， 2011： 78-83. DOI： 10.1109/ESTS.2011.5770845.

[7]郭燚， 楊濤. 超級電容儲能在船舶中壓直流系統能量管理中的應用[J]. 上海海事大學學報， 2016， 37（4）： 75-81. DOI： 10.13340/j.jsmu.2016.04.014.

[8]STEUER M， BOGDAM F， BOSWORTH M， et al. Multifunctional megawatt scale medium voltage DC test bed based on modular multilevel converter （MMC） technology[J]. IEEE Transactions on Transportation Electrification， 2016， 99： 1-1. DOI： 10.1109/ESARS.2015.7101535.

[9]CHEN Yu， LI Zuoyu， ZHAO Shanshan， et al. Design and implemenation of a modular multilevel converter （MMC） with hierarchical redundancy ability for electric ship MVDC system[J]. IEEE Journal of Emerging & Selected Topics in Power Electronics， 2017， 5（1）： 189-196. DOI： 10.1109/JESTPE.2016.2632858.

[10]GLINKA M， MARQUARDT R. A new AC/AC-multilevel converter family applied to a single-phase converter[C]//International Conference on Power Electronics and Drive Systems. IEEE Xplore， 2003： 16-23. DOI： 10.1109/PEDS.2003.1282669.

[11]孫廣星， 茍銳鋒， 孫偉. 基于MMC結構的電力電子變壓器拓撲結構及控制策略研究[J]. 高壓電器， 2016， 52（1）： 142-147. DOI： 10.13296/j.1001-1609.hva.2016.01.024.

[12]徐政. 柔性直流輸電系統[M]. 北京： 機械工業出版社， 2013： 122-123.

[13]趙成勇， 許建中， 李探. 全橋型MMC-MTDC直流故障穿越能力分析[J]. 中國科學， 2013， 43（1）： 106-114.

[14]TEEUWSEN S P. Modeling the trans bay cable project as voltage-sourced converter with modular multilevel converter design[C]//Power and Energy Society General Meeting. IEEE， 2011： 1-8. DOI： 10.1109/PES.2011.6038903.

[15]孫立明， 駱亮， 王沁， 等. 上海柔性直流接入系統的電網運行方式探討[J]. 華東電力， 2011， 39（11）： 1838-1841.

[16]楊光豪. 基于MMC的直流輸電系統控制方法研究[D]. 杭州： 浙江工業大學， 2015.

[17]TU Qingrui， XU Zheng， XU Lie. Reduced switching-frequency modulation and circulating current suppression for modular multilevel converters[J]. IEEE Transactions on Power Delivery， 2011， 26（3）： 2009-2017. DOI： 10.1109/TPWRD.2011.2115258.

[18]王也仿. PWM整流器的直接電流控制策略和控制器的設計[J]. 科技通報， 2005， 21（5）： 580-583. DOI： 10.13774/j.cnki.kjtb.2005.05.020.

[19]GUAN Minyuan， XU Zheng. Modeling and control of a modular multilevel converter-based HVDC system under unbalanced grid conditions[J]. IEEE Transactions on Power Electronics， 2012， 27（12）： 4858-4867. DOI： 10.1109/TPEL.2012.2192752.

[20]謝龍裕， 羅安， 徐千鳴， 等. 基于MMC的STATCOM控制方法[J]. 電網技術， 2014， 38（5）： 1136-1142. DOI： 10.13335/j.1000-3673.pst.2014.05.002.

[21]ROWEN W I. Simplified mathematical representations of heavy-duty gas turbines[J]. Journal of Engineering for Gas Turbines & Power， 1983， 105（4）： 865-869. DOI： 10.1115/1.3227494.

[22]HANNETT L N， KHAN A. Combustion turbine dynamic model validation from tests[J]. IEEE Transactions on Power Systems， 1993， 8（1）： 152-158. DOI： 10.1109/59.221261.