最大稀布平面陣的WOA綜合
袁鵬亮
(1. 慶陽職業技術學院 能源工程系,甘肅 慶陽745000;2. 西北工業大學 電子信息學院,陜西 西安 710129)
陣列綜合是根據系統所要求的天線指標、波束形狀等來求解天線的陣元間距、激勵幅度和相位等參數的過程.可以看出,陣列綜合是天線設計的逆向過程.在通信、射電天文望遠鏡以及衛星通信等應用中,通常要求天線輻射的波束形狀具有主瓣寬度盡可能窄、旁瓣峰值電平(PSLL, peak sidelobe level)盡可能的低的特點,這樣的波束特點一方面可以減小降低對消工作過程中的環境噪聲及人為干擾,提高傳輸的質量和效率,另一方面,窄波束比寬波束更節省功率,方向性更好[1].
實現以上波束形狀一般有硬件和軟件兩種實現途徑.硬件實現不可避免的會抬高設備的復雜度和造價成本,于是一般采用軟件的方式.軟件的方式來做綜合天線陣列,大致有數值法和解析法兩類.解析法對于許多實際的工程問題來說過于復雜,且影響因素多是未知,解析求解精確值根本不可能實現,造成解析法的難以應用.數值法隨著計算機技術的發展興起,尤其是算法研究的突飛猛進,開始被陣列綜合廣泛采用.特別是對于參數要求不太高的情況,這使得工程應用更為經濟便利[2].
迄今為止,陣列綜合已經有七十多年的研究歷史.多種隨機的、進化型、單目標和多目標的算法陸陸續續被引入到研究當中,例如,遺傳算法(GA,genetic algorithm)、粒子群算法(PSO,particle swarm algorithm)、差分進化算法(DE,differential evolution algorithm)等.
在文獻[3]中,利用GA方法對16陣元均勻間距的線陣和16×16陣元的矩形平面陣進行了優化,優化變量是激勵幅度,實現給定PSLL的方向圖綜合.與Taylor綜合方法相比,綜合相同的方向圖,速度有了提高.在文獻[4]中,采用GA算法對稀疏平面陣做了綜合,約束條件是陣元間距大于半波長.采用0°和90°方位的PSLL和作為適應度目標函數.這里的陣元總數目為108,孔徑約束規格在9.5λ×4.5λ.
在文獻[5]中,引入PSO方法到稀布陣的綜合,考慮的是奇數陣元對稱線陣的陣元間距優化,約束條件是獲得盡可能低的最大PSLL.在文中,將PSO算法的交叉、變異操作環節去除,改進后的PSO算法更快,取得了比以前更好的優化結果.不足之處在于優化的陣列數目較小.
在協同搜索算法(harmony search algorithm)基礎上改進的DE算法綜合線性非周期陣列見于文獻[6].通過在經典的DE算法中加入參數選擇策略,結合了DE算法較好的區域搜索能力和協同搜索算法的好的搜索多樣性.該復合算法有較快的收斂速度,計算負荷也較小.
鯨算法WOA(Whale Optimization Algorithm)是一種最近提出的新的隨機仿生優化算法[7],在對單目標的優化上有較為明顯的效率優勢.并且,優化結果較好,也有較高尋優命中率.本文就最大矩形平面陣的WOA綜合方法做了研究.
1 問題描述
1.1 陣列模型
現在我們考慮一個陣元數目為4N的可分離的矩形平面陣,陣列的陣元排列限定在2L×2H(L是矩形長,H是矩形寬)范圍.陣列的陣元表示采納球坐標系(見圖1).每個陣元在坐標系中的位置可以表示為(rn,θn,φn),陣元在XOY坐標平面以原點對稱分布,那么其遠場輻射方向圖為
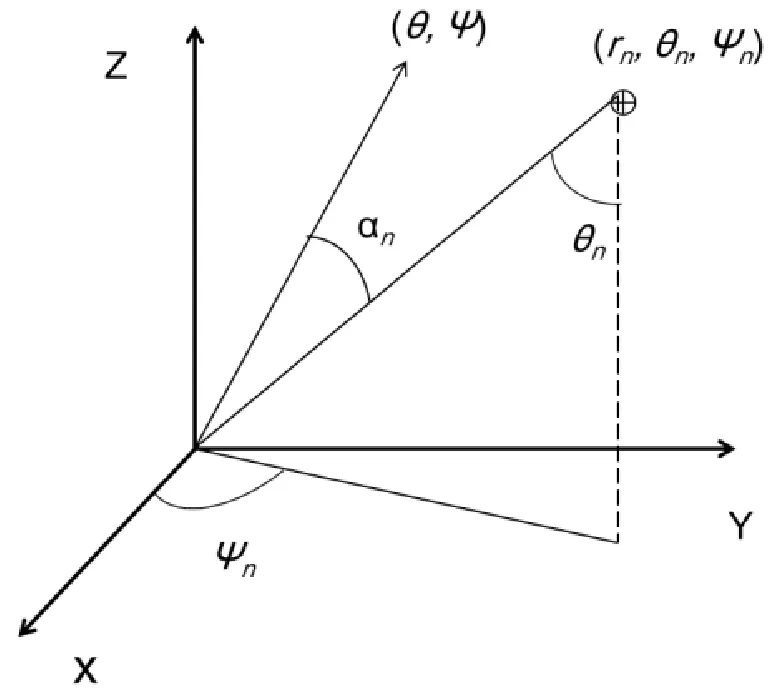
圖1 天線陣的坐標系統
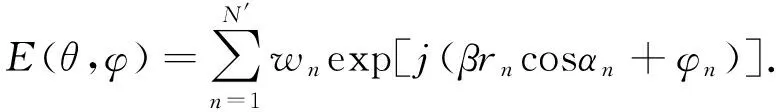
(1)
在此,wn為激勵幅度,相應的激勵相位φn,β=2π/λ為波數,λ是波長.若令
cosαn=sinθsinθncos(φ-φn)+cosθcosθn,θ∈[0,π],φ∈[0,2π].
(2)
假設陣元采用均勻等幅激勵,wn=1,φn=0.根據給定的陣列幾何形狀,則表達式(1)改寫為
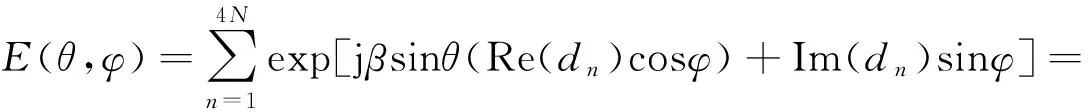
(3)
根據(2),當φ=0,(3)的具體形式可以表示為
(4)
相似的,在φ=π/2,(3)的具體形式可以表示為
(5)
本文優化的目標是取得在PSLL最低時的陣列陣元的排布參數,取E(θ,0)與E(θ,π/2)的和最大值作為適應度函數,那么,這里的約束性優化問題就可以定義為
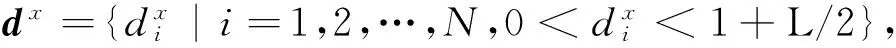
(6)
1.2 WOA算法
WOA算法是一種最近新提出的仿生優化算法,其靈感來源于海洋中的座頭鯨的捕獵行為.該算法是基于隨機搜索來得到最優解的,主體結構包含三個組成部份:圍取目標、螺旋形泡泡網反饋策略、搜索目標.算法主要流程見圖2.
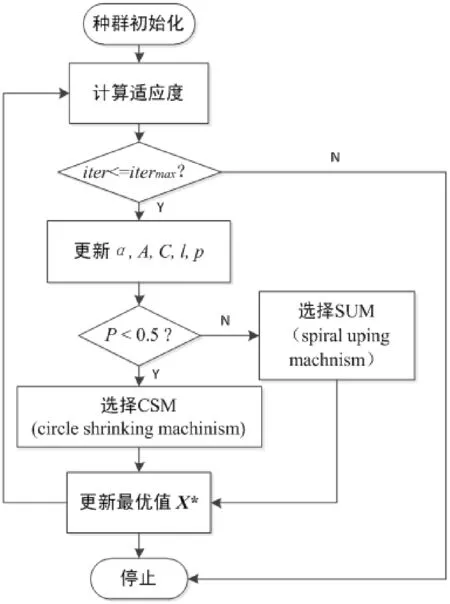
圖2 WOA算法的流程圖
1.2.1 圍取目標
初始化種群.若d為一個矢量,其表示為d={d1,d2,…,dn}.又令x=d,則
x=(x1,x2,…,xn)T,?xn∈R,
y=(θ1,θ2,…,θr)T,?θn∈Θs.
(7)
Θ2表示天線方向圖的旁瓣區域.在進行優化時,若初始種群規模設定為m,優化變量個數為n,那么種群的維度就應為m×n,具體可以表示為
(8)
現在我們可以令
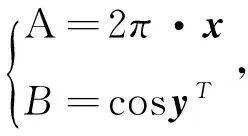
若x(t)是當前的優化變量,x*(t)為本次迭代時的最優解,其主要行為由以下表達來概括.
(9)
1.2.2 反饋策略
內含兩個步驟:環縮小策略(circle shrinking mechinism,CSM),螺旋上升策略(spiral upingmechinism,SUM).
為了模仿隨機性P取隨機值.當p<0.5,選擇CSM來搜索可行解;否則,選擇SUM來搜索可行解.
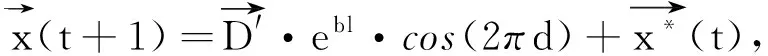
(10)
1.2.3 搜索目標
在自然界中座頭鯨的搜索隨機性主要取決于彼此間的具體位置.為此,這里利用A的隨機值來實現遠離參考鯨當前位置.其數學模型如下:
(11)
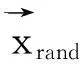
WOA算法主要的控制參數是A、C,控制參數相對較少,其優點是計算速度快效率高,易于實現.
2 仿真結果及討論
在此我們考慮一個對稱的矩形平面陣,陣元個數為108,孔徑約束規格為2L×2H=9.5λ×4.5λ.在, 取樣100,分辨率為0.9°.優化變量的上下界分別設定為4.75、0.25,迭代最大次數選擇50次.
優化得到的最優解對應的遠場輻射方向圖如圖3所示,小圖為φ= 0°和90°的各自對應的輻射方向圖,主圖為兩者副瓣區域電平值和的輻射方向圖.在文獻[4]中,本例的GA算法優化得到的最優適應度值為-45.456 dB(φ= 0°平面的PSLL為-29. 597 dB,φ= 90°平面的PSLL為-15.859 dB).本文的WOA算法得到的單個方向圖中最大PSLL為-48.65 dB(φ=0°平面的PSLL為-20.29 dB,φ=90°平面的PSLL為-28.36 dB).與文獻[4]相比,在最優適應度值上降低了3 dB,φ=0°平面和φ=90°平面的PSLL都分布在-20 dB以上.圖4為優化得到的陣元位置分布,可以看出,陣元隨機的分布在第一象限的平面.
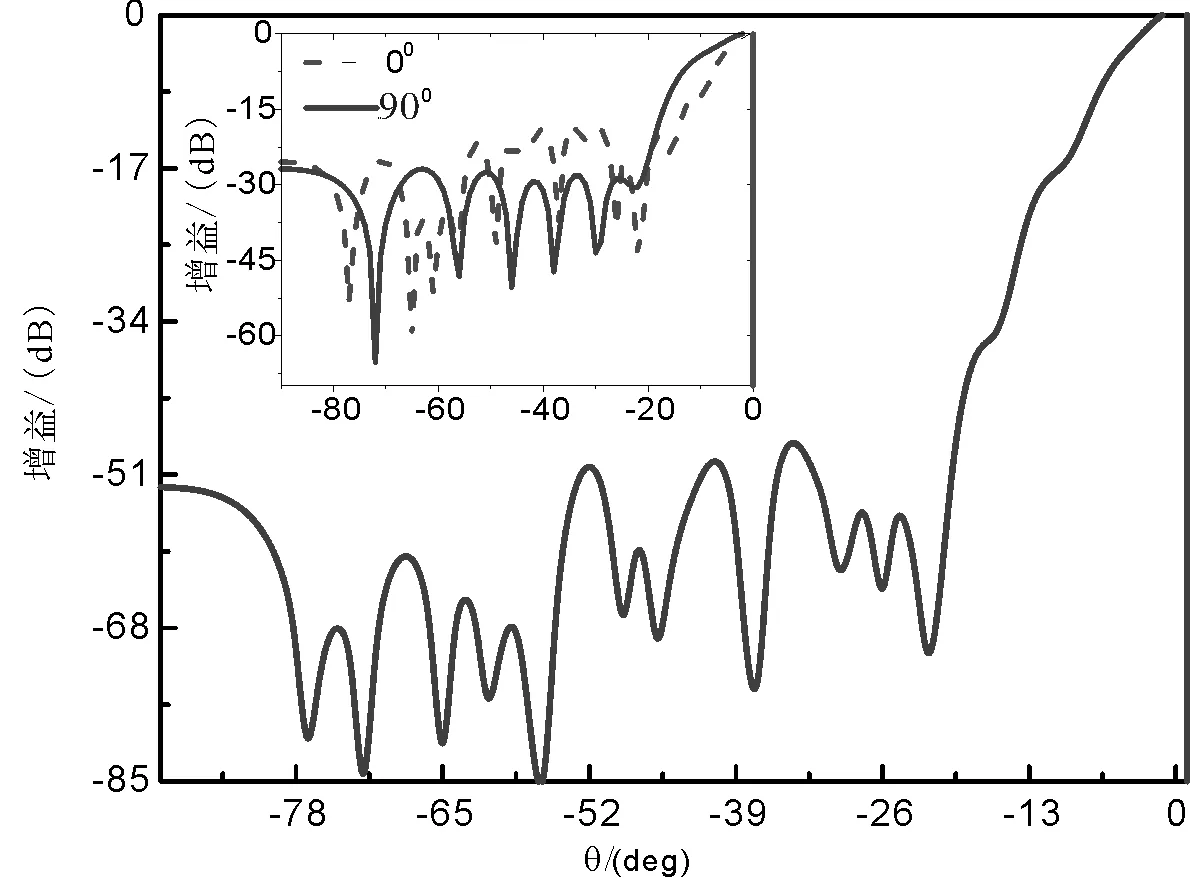
圖3 最終優化結果對應的方向圖
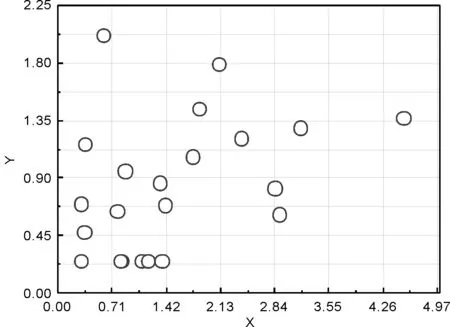
圖4 陣元位置分布
為證實WOA方法的穩健性,列出了最優結果迭代過程的收斂曲線(圖5),以及最后3次單獨運行的收斂曲線與平均收斂曲線的對比圖(圖6),可以看出,WOA算法是有效且穩健的.
3 結語
WOA算法作為一種新提出的算法,目前為止在陣列綜合中還沒有應用.本文就WOA算法引入到最大稀布矩形平面陣的陣元位置的綜合,由于矩形平面陣在等幅激勵的情況下即是可分離的,可以等效為兩個維度上的線陣綜合,與WOA算法結合,不考慮互耦效應和陣元間距約束的情況下,取得了較GA算法更優的結果.WOA算法目前僅是一種只能優化單目標的算法框架,如何應用于多目標問題將是后續的可探討的問題.
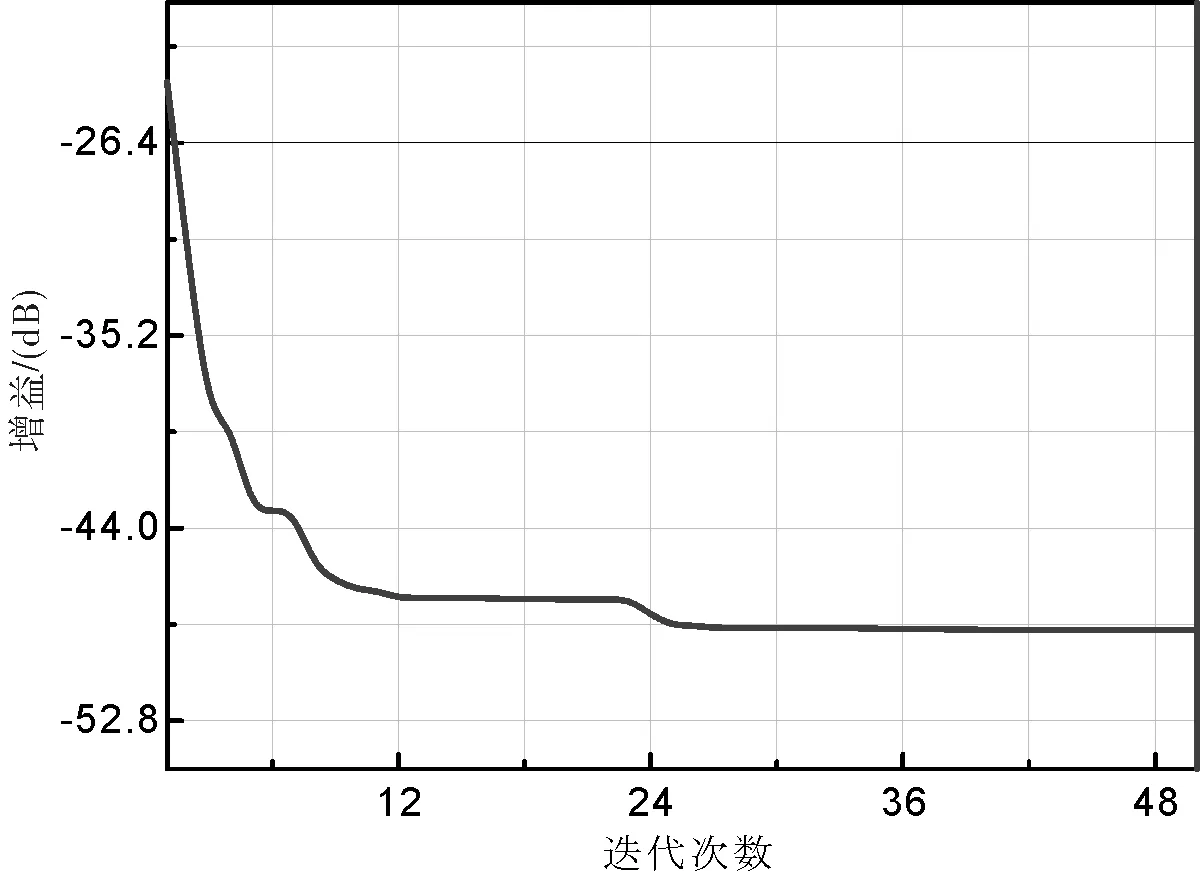
圖5 最終得到的優化結果的收斂曲線
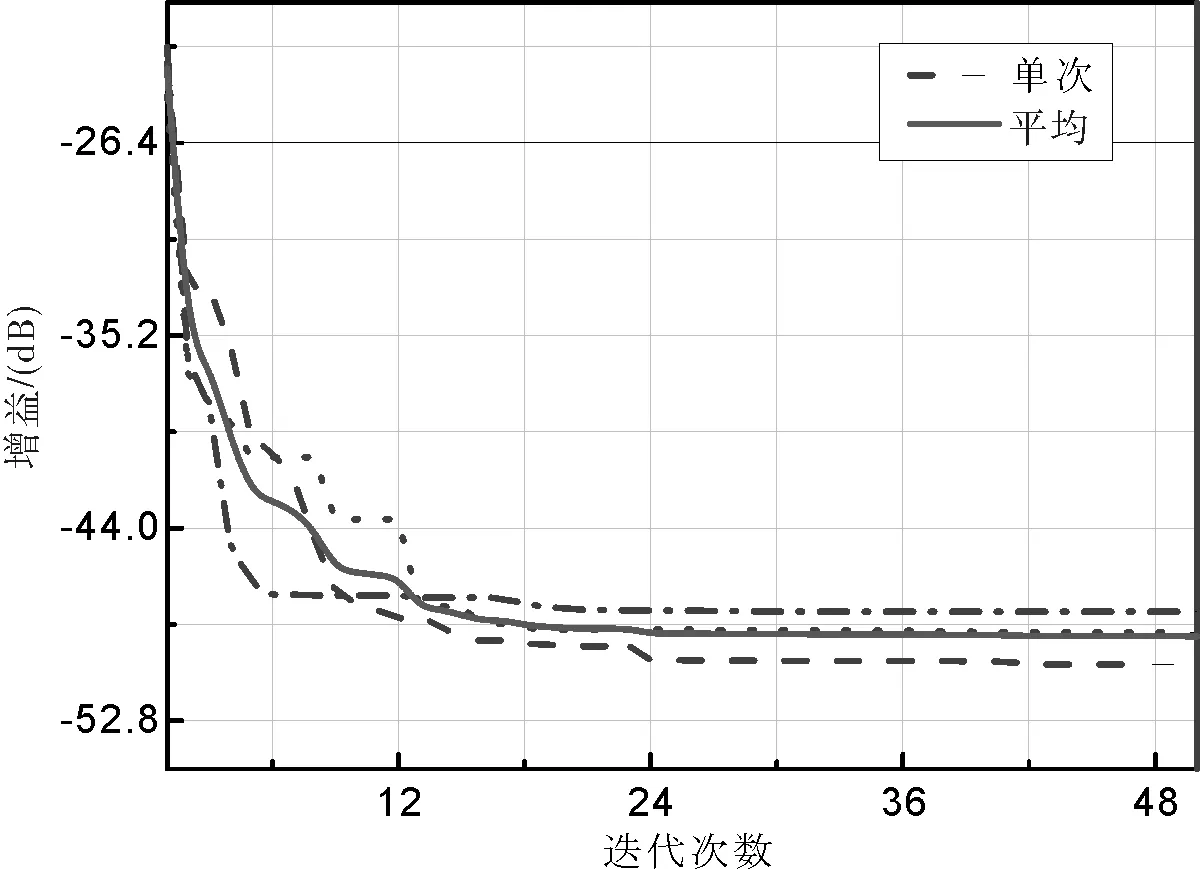
圖6 單次與平均收斂曲線
參考文獻:
[1] 呂善偉.天線陣綜合[M].北京:北京航空學院出版社,1988.
[2] 袁亞湘,孫文瑜.最優化理論與方法[M].北京:科學出版社, 1997.
[3] 邊 莉,車向前,楊國輝,等.基于遺傳算法的低副瓣陣列天線綜合[J].計算機應用,2008, 28(7): 1 656-1 658.
[4] 陳客松,何子述.平面稀布天線陣列的優化算法[J].電波科學學報, 2009, 24(2): 193-198.
[5] 劉姜玲,王小謨.改進粒子群算法綜合有間距約束的稀布陣列[J].微波學報, 2010, 26(5): 7-10.
[6] Zhang F, Jia W, Yao M. Linear Aperiodic Array Synthesis Using Differential Evolution Algorithm[J]. IEEE Antennas & Wireless Propagation Letters, 2013, 12(9): 797-800.
[7] Mirjalili S, Lewis A. The Whale Optimization Algorithm[J]. Advances in Engineering Software, 2016, 95(3):51-67.

