不確定CTO系統訂單承諾決策研究

孫德廠

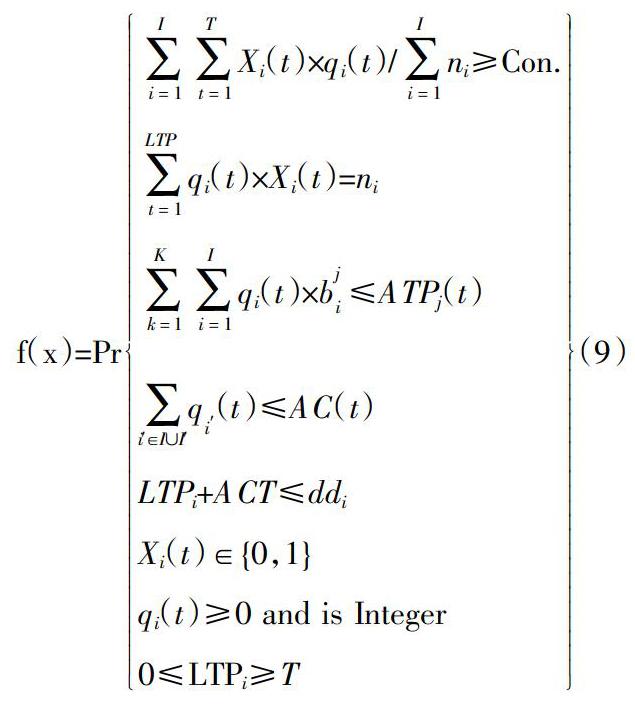
【摘 要】CTO系統中，受不確定因素影響，訂單接受率、訂單承諾可靠性、準確性不高。為解決此問題，首先，分析不確定因素對訂單承諾的影響，構建基于可承諾量/可承諾能力的訂單承諾流程。然后，建立了隨機相關機會規劃訂單承諾模型。最后，將模型和算法應用于某整車生產企業，提升了訂單接受率、訂單承諾可靠性和準確性。

【Abstract】 Under the influence of the uncertain factors， the order acceptance rate， the reliability and the accuracy of the order promise are often not high in CTO system. To improve the decision-making problem， based on the analysis of the influence of uncertain factors on the order promise， we should build an order promise process based on the Available-to-Promise/Capable-to-Promise. Then， an order promise model of random correlation opportunity planning is established. Finally， the model and algorithm are applied to a vehicle production enterprise to enhance the order acceptance rate， reliability and accuracy of order promise.

【關鍵詞】訂單承諾；可承諾量；可承諾能力

【Keywords】order promise； Available-to-Promise； Capable-to-Promise

【中圖分類號】F273 【文獻標志碼】A 【文章編號】1673-1069（2018）03-0182-05

1 引言

按訂單配置（Configure-to-Order， CTO）是按訂單裝配（Assemble-to-Order， ATO）的一種特殊形式，二者具有相同的顧客訂單分離點（Customer order decoupling point， CODP），通過延遲裝配控制庫存和交貨期。二者的區別是，前者提供部分零部件的多個選項供顧客選擇，進行配置，能夠在較大程度上滿足客戶的個性化需求，而后者為客戶提供標準化的配置產品供客戶選擇。CTO生產系統由兩部分構成，即零部件庫存補充系統和最終產品裝配系統。零部件庫存補充系統采用外購或/和內部生產，根據預測數據進行庫存控制，內部生產采用推式；最終產品裝配采用拉式，由客戶訂單驅動。CTO生產系統是典型的推拉結合的混合生產系統，普遍存在于汽車、電子等行業[1]。

伴隨著ATO/CTO生產方式的廣泛應用和日漸成熟，學術界和實務界關注焦點也從最初的系統構建[2]、特征刻畫[3]、績效分析[4-6]轉向外部供應鏈協調，訂單承諾即是其中的熱點之一。訂單承諾決策，在更多的文獻里也稱為訂單接受、訂單選擇、生產決策等，這方面的研究主要從三方面展開，即：面向庫存控制的可承諾量（Available-to-Order， ATP）[7，8]，面向產能分配的可承諾能力（Capacity-to-Order， CTP）[9，10]，面向收益管理的可承諾利潤（Profitable-to-Order， PTP）[11]，以及他們之間相互纏繞的情形[12，13]。對ATO/CTO系統不確定性要素的研究主要有提前期[4]、裝配能力[10，14]，客戶需求[14，15]等，其研究方法有：數學規劃、系統仿真等。

研究內容安排如下：引言部分對CTO/ATO生產系統特征進行介紹，并綜述CTO/ATO環境下訂單承諾問題研究現狀。第2部分，在分析不確定要素對訂單承諾影響的基礎上，給出基于ATP/CTP分配機制的訂單承諾流程。第3部分，建立基于隨機相關機會規劃的訂單承諾模型，并運用混合智能算法進行求解。第4部分，以實際生產環境，基于歷史數據進行案例研究，并進行對比分析。最后，給出本研究的結論及展望。

2 CTO系統訂單承諾決策問題分析

2.1 訂單承諾決策空間

CTO環境下訂單承諾決策，從企業業務角度看，是一個戰術層決策問題。從信息系統角度，是一個決策支持系統。訂單承諾決策空間包括客戶響應空間和企業資源空間。客戶響應空間，輸入是客戶需求，即客戶訂單；輸出是訂單承諾的數量和交貨期。企業資源空間，輸入是各種企業資源；輸出是承諾訂單對資源占用及生產計劃，如圖1所示。

2.2 不確定性對訂單承諾的影響分析

不確定性指在有限時間范圍內的不可預知事件，具有難以定量表達、難以預測的特點 [16，17]。對生產系統而言，指任何干擾生產計劃順利執行的不可預知的事件。不確定性分為兩種類型：環境不確定性、系統不確定性。環境不確定性指生產過程之外的不確定性，即不受企業嚴格控制的外部因素；系統不確定指生產過程不確定，存在于企業內部。從訂單承諾的角度而言，CTO生產系統不確定要素主要是通過影響零

部件的可承諾量、產成品可承諾裝配能力和裝配周期，進而影響客戶訂單數量、交貨期承諾。詳細影響機制如圖2所示。

2.3 基于ATP/CTP分配的訂單承諾流程

CTO模式下，必須同時考慮零部件可承諾量、最終產品可承諾裝配能力兩個變量，這是一個相互纏繞的問題，往往存在零部件充足而產品裝配能力不足的情況，反之亦然。為使成品裝配能力得到最大化利用、控制零部件庫存，訂單承諾決策流程如下：

步驟1：根據銷售預測，展開零部件需求計劃、最終成品裝配能力計劃。

步驟2：根據零部件需求計劃，計算零部件可承諾量。由于庫存、生產、供應的不確定性，零部件可承諾量是一個服從某種分布的隨機變量，其分布特征通常采用歷史數據分析、擬合的方法得到。

步驟3：根據成品裝配能力計劃，計算可承諾裝配能力。由于機器、人員能力的不確定性，可承諾裝配能力也是服從某種分布的隨機性變量，其分布特征同樣采用歷史數據分析、擬合的方法得到。

步驟4：根據客戶訂單數量、產品配置、交貨期，進行訂單分解，計算零部件需求量、成品裝配能力需求量，并估算該特定配置產品的裝配周期。

步驟5：基于零部件可承諾量對各個訂單的零部件需求進行優化分配。對于零部件需求不能滿足的訂單，轉步驟7，拒絕該訂單或與客戶進行協商。對于零部件需求能夠滿足的訂單，轉步驟6。此處，需要反復進行分配優化。

步驟6：對物料需求得到滿足的訂單，根據可承諾裝配能力進行優化分配。對于優化結果，如果滿意，對裝配能力需求不能滿足的訂單，轉步驟7，對于裝配能力需求滿足的訂單轉步驟8。如果不滿意，轉步驟5，再次對零部件進行分配。此處需要反復進行分配優化。

步驟7：針對零部件需求不能滿足或零部件需求滿足而裝配能力不能滿足的訂單，與客戶進行協商或拒絕。

步驟8：針對零部件需求、裝配能力需求均能滿足的訂單，對客戶輸出承諾數量、交貨期，對生產系統輸出上線時間、零部件、成品裝配能力預留。

3 模型構建與求解

3.1 隨機相關機會規劃訂單承諾模型

對不確定性變量的定量描述數學方法有隨機變量、模糊變量、粗糙變量以及他們的多重變量[18]。在構建含有隨機變量的優化問題建模中，隨機規劃是一個有效的工具，包括三個分支：①丹澤于1955年提出，康托洛維奇發展出來的期望值模型。②查納斯和庫伯于1959提出的機會約束規劃。③劉寶碇于1997年提出的隨機相關機會規劃。

基于ATP/CTP分配的訂單承諾流程、隨機規劃的相關理論基礎，本文構建基于隨機相關機會規劃的訂單承諾決策模型如下：

模型假設：

①CTO生產系統包括兩個階段，零部件庫存與成品裝配；

② 一個客戶訂單僅包含一種產品；

③系統僅有零部件庫存，沒有成品庫存；

④ 零部件需求計劃和成品裝配能力計劃有銷售預測驅動，即客戶訂單不引起相關需求；

⑤CTO生產系統的不確定性包括零部件可承諾量、可承諾裝配能力、裝配周期；

⑥零部件指每個訂單產品的關鍵零部件，成品裝配能力指裝配工序的瓶頸工序能力；

⑦CTO生產系統處于均衡負荷狀態；

⑧訂單只能全部接受，不能被部分接受。

索引與集合：

I： 新到達客戶訂單集合，i∈I；

I′：已承諾訂單集合，i′∈I∪I′；

k： 零部件類型，k∈K；

J：第k類零部件的零部件索引，j∈Jk；

T： 計劃周期，t∈T。

參數：

ni：訂單i的數量；

ddi：訂單i的交貨期；

bij：訂單i中，零部件j的需求數量；

CTP（t）：時刻t可承諾裝配能力，服從某種隨機分布；

ACT：裝配周期，服從某種隨機分布；

Con.： 常量值；

ATPj（t）：零部件j時刻t的可承諾量，服從某種隨機分布；

決策變量：

Xi（t）=1，如果訂單i在時刻t被承諾0，否則；

qi（t）：時刻t訂單i被承諾的數量；

LTPi：訂單i被承諾的最后時間；

目標函數：

目標函數是最大化訂單接受率，其含義是最大化最終產品裝配能力利用率。目標函數如公式（1）。

約束（2）表示訂單在所有的時段中被承諾的量之和，等于訂單數量。約束（3）表示，對包含物料的訂單在所有時段的承諾量，必須小于等于物料的可承諾量，服從某種隨機分布。約束（4）表示在每個時段承諾的訂單產品數量之和小于等于該時段可承諾裝配能力，服從某種隨機分布。約束（5）表示訂單被承諾的最晚的日期加上裝配周期，必須小于等于訂單的交貨日期。約束（6）表示決策變量Xi（t）是0～1變量。約束（7）表示決策變量qi（t）是大于等于零的整數。約束（8）表示決策變量LTPi必須在訂單承諾的周期范圍內。

3.2 混合智能算法

求解隨機相關機會規劃模型，目前主要有兩種方法，一類是轉化法，即將隨機規劃轉化成各自的確定性等價類，然后利用已有的確定性規劃的求解方法解之；另一類是逼近方法，利用隨機模擬技術，通過一定的智能優化算法，得到隨機規劃問題的近似最優解和目標函數的近似最優值。由于在做模型求解時，有些問題從隨機規劃到確定性等價類的轉換并不總是奏效，而且已有的確定性規劃求解方法自身的局限性，如不適合求解大規模問題，求解速度慢，需要深刻數學理論基礎，不便于計算機程序實現等。本文對劉寶碇教授提出的混合遺傳算法進行適應性改造，主要步驟如下：① 根據不確定性原理，構建機會函數，公式（9）；②使用Mo∈∈nte Carlo隨機模擬方法，根據隨機變量的分布特征，生成隨機樣本數據；③用隨機模擬的樣本數據訓練神經網絡逼近不確定函數（機會函數）；④使用業務規則，初始化染色體種群，利用訓練好的不確定函數檢驗每個染色體的可行性；⑤通過交叉和變異操作更新染色體，并利用訓練好的神經元網絡檢驗子代染色體的可行性；⑥ 利用訓練好的不確定函數計算所有染色體的目標值；⑦ 根據目標值計算每個染色體的適應度；⑧通過旋轉輪盤賭選擇染色體；⑨重復步驟（4）到（8）直至滿足終止條件；⑩給出最好的染色體作為最優解。

4 案例研究

4.1 實驗方案及數據準備

為檢驗所構建的基于ATP/CTP分配的隨機相關機會規劃訂單承諾模型以及混合智能算法的可靠性、準確性，針對某客車裝配企業，選取歷史數據中的10個訂單進行驗證。為便于演示和減少數據規模，選擇關鍵零部件作為示例。對汽車整車配置，選擇底盤和車身6個配置項，14個零部件，其中底盤配置項為必選項，車身配置項為可選項。車型配置結構如圖3所示，配置項括號中數字為單車物料需求數量。表1給出訂單的基本信息，主要包括訂單數量、交貨期和車型配置實例。表2給出了隨機變量的分布特征，根據歷史數據分析、擬合，零部件可承諾量、成品可承諾裝配能力服從均勻分布，裝配周期服從非負二項分布。計劃周期為1周，時段以天為單位，1周5個工作日。

4.2 實驗執行

根據混合智能算法流程，首先，將實驗數據帶入模型，并構造機會函數。其次，隨機模擬5000次，產生5000個數據樣本。再次，使用數據樣本訓練神經網絡，逼近不確定函數，最大訓練次數為2000次，隱含層神經元個數為78個，訓練精度為0.1。最后，將訓練好的不確定函數作為評價函數，使用遺傳算法進行搜索。初始種群為30，交叉概率，變異率，最大迭代次數為2000，運算后的數據進行整理，訂單承諾結果如表3所示。

4.3 實驗分析

SDCPOP與FCFS、LDP規則比較。采用上述同一訂單承諾案例，使用常用業務規則：先到先服務（First Come First Server，FCFS）、最長交期優先（Longest Delivery Priority，LDP）進行訂單承諾，相關指標如表4所示。訂單接受率分別提升60%、33%；訂單產品接受數量分別提升42%、36%；完工時間與交貨期一致性訂單比率均提升150%；完工時間與交貨期一致性訂單產品數量比率分別提升67%、51%；提前完工訂單產品數量加權天數分別降低47%、57%；裝配能力利用率分別提升43%、26%。SDCPOP模型具有較大的優越性。

5 結論

針對不確定CTO系統下訂單承諾決策質量不高的問題，提出一種基于ATP/CTP分配的隨機相關機會規劃訂單承諾模型，運用混合智能算法求解模型。模型能夠為客戶提供訂單數量和交貨期承諾，為企業提供上線時間制定，零部件可承諾量、可承諾裝配能力預留，為訂單承諾決策者提供支持。通過實際案例研究，與FCFS、LDP規則相比，可以提升訂單接受率，訂單承諾可靠性、準確性。同時表明，必須考慮系統不確定性，才能提升訂單承諾質量，提升客戶服務水平。

由于訂單承諾是一個復雜的決策問題。對外，涉及客戶服務水平、供應鏈協調；對內，涉及生產資源優化、生產效率提升。本文主要研究CTO系統內部要素對訂單承諾的影響，如何考慮決策者偏好、客戶偏好、客戶訂單等環境要素，需要將模型進一步擴展。此外，如何提高訂單盈利水平也需要深入研究。

【參考文獻】

【1】Omar Ghrayeb， Nipa Phojanamongkolkij， Boon Aik Tan. A hybrid push-pull system in assemble-to-order manufacturing environment [J]. Journal of Intelligence Manufacture， 2009（20）： 379-387.

【2】Jing-Sheng Song， Paul Zipkin. Supply Chain Operations： Assemble-to-Order Systems [M]. Handbooks in Operation Research & Management Science， 2003.

【3】F. Alarcón， M.M.E. Alemany， A. Ortiz. Conceptual framework for the characterization of the order promising process in a collaborative selling network context [J]. International Journal of Production Economics. 2009 （120）：100-114.

【4】Jing-Sheng Song， David D. Yao. Performance analysis and optimization of assemble-to-order systems with random lead times [J]. Operation Research， 2002 ，50（5）： 889-903.

【5】Fernando Bernstein， Gregory A. DeCroix， Yulan Wang. The Impact of Demand Aggregation through Delayed Component Allocation in an Assemble-to-Order System [J]. Management Science， 2011， 57（7）： 1154-1171.

【6】楊水利，周孫福，李韜奮. 客戶訂單多分離點對加工裝配型產品的生產成本影響研究——裝配延遲視角[J]. 運籌與管理，201019（3）：144-150.

【7】Kune-muh Tsai， Shan-chi Wang. Multi-site available-to-promise modeling for assemble-to-order manufacturing：An illustration on TFT-LCD manufacturing [J]. International Journal of Production Economics， 2009（117）： 174-184.

【8】Juin-Han Chen， Chin-Tai Chen. Using Mathematical Programming on Two-Phase Order Promising Process with Optimized Available-To-Promise Allocation Planning [J]. International Journal of the Computer， the Internet and Management， 2009， 17（3）： 25-40.

【9】Ann Bixby， Brian Downs， Mike Self. A Scheduling and Capable-to-Promise Application for Swift & Company [J]. Interfaces ，2006，36（1）：69-86.

【10】Yongbo Xiao， Jian Chen， Chung-Yee Lee. Optimal decisions for assemble-to-order systems with uncertain assembly capacity [J]. International Journal of Production Economics， 2010（123）： 155-165.

【11】Frederick Faber. An Extensible Order Processing and Revenue Management Testbed [D]. University of Maryland， College Park， Masters of Science， 2005.

【12】Anne Gillian Robinson. Real-time ATP/CTP： Policies for Dynamic Order Promising [D]. Stanford University， Doctor of Philosophy，2005.

【13】Juin-Han Chen， James T. Lin， Yi-Sheng Wu. Order Promising Rolling Planning with ATP/CTP Reallocation Mechanism [J]. IEMS ，2008（7）：57-65.

【14】肖勇波，陳劍，吳鵬. 產能和需求不確定情形下ATO系統最優庫存和生產決策研究[J].中國管理科學，2007，15（5）：56-64.

【15】吳鵬，呂有廠. 隨機需求下考慮半成品庫存的多周期生產決策優化[J]. 運籌與管理，2014，（4）：49-54.

【16】Brian Daniel Keller. Models and Methods for Multiple Resource Constrained Job Scheduling under uncertainty [D]. The University of Arizona， 2009.

【17】S. C. L. Koh， S. M. Saad. Development of a business model for diagnosing uncertainty in ERP environments [J]. International Journal of Production Research， 2010， 40（13）：3015-3039.

【18】Liu Baoding. Dependent-chance goal programming and its genetic algorithm based approach [J]. Computers Mathematical Application， 1997，34（12）： 89-104.