MT阻抗張量在二維與三維介質中的分析

胡瑋哲， 熊高君

(成都理工大學 地球物理學院 成都 610059 )

0 引言

大地電磁測深法(Magnetotelluric ,MT)是20世紀50年代初，由前蘇聯學者A.T.Tikhonov[1]與法國地球物理學家L.cagnird[2]分別提出，以天然交變電磁場為場源來獲取有關地下地質體的電性結構特征的信息，屬于頻率域測深的一種方法。通過對二維以及三維的阻抗張量的分析來表征地球系統的傳輸性質以及描述其地質意義。傳統的處理方法是將Z(阻抗張量)進行旋轉分析，一般可以滿足對二維構造問題的研究。但三維的分析只能將其近似的表現為二維介質來研究，所以Z的旋轉分析效果是有限的。在阻抗張量的分析方法中，Swift[3]提出了對阻抗張量的傳統分解方法,通過對觀測坐標的旋轉，使得阻抗張量的對角最小或者反對角元素最大，由此求得構造主軸方位以及阻抗大小；Yee[4-5]利用數學上的奇異值分解方法推導出阻抗張量Z的正則分解形式，既結合了傳統旋轉分析的基礎又拓展了對阻抗張量地質意義的認知；國內對大地電磁測深法的真正應用起始于20世紀70年代，于20世紀初王光鍔[6]闡述了阻抗張量的正則分解與傳統分析方法的等價性條件。由于電磁場于三維介質傳播的復雜性，目前國內、外對三維介質阻抗張量的研究正在進行。筆者通過分析二維與三維介質的阻抗張量，來闡述對阻抗張量的意義。

1 二維介質阻抗張量的分析

1.1 Z的旋轉分析

(1)

旋轉后所得的阻抗張量：

Z(θ)=[u]·Z·[u]T

(2)

即可得

(3)

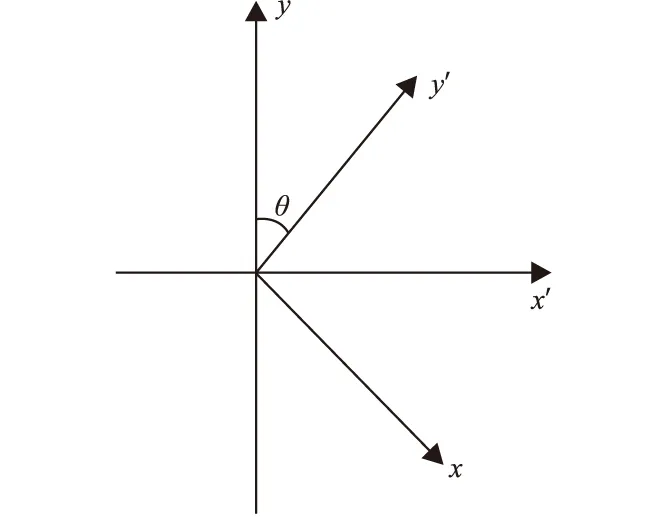
圖1 坐標變換示意圖Fig.1 Coordinate transformation

由式(3)可以令：

Zxx(θ)=Z2-Z1cos 2θ+Z4sin 2θ

Zxy(θ)=Z3-Z1sin 2θ+Z4cos 2θ

Zyx(θ)=-Z3+Z1sin 2θ+Z4cos 2θ

Zyy(θ)=Z2+Z1cos 2θ-Z4sin 2θ

(4)

其中

(5)

若經過旋轉角θ0觀測坐標系與二維介質電性主軸重合，則

Zxx(θ0)=0,Zxy(θ0)=ZTE

Zyx(θ0)=-ZTM,Zyy(θ0)=0

(6)

但在實際觀測中Zxx(θ0)、Zyy(θ0)不可能為“0”，所以可構造函數F(θ)使得

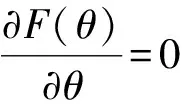
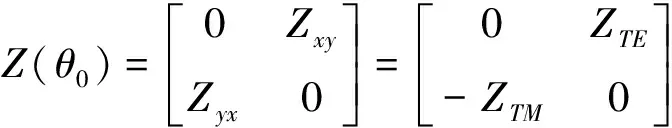
(7)

所以在二維介質中，通過對觀測坐標系中的阻抗張量進行旋轉分析可以獲得旋轉角度θ0，從而可以確定二維介質的電性主軸所在的正交方位。

1.2 的SVD分解

由Z代數中矩陣的奇異值分解原理可知[8]，對阻抗張量可進行如下分解：

Z=U·∧·V+(+表示轉置共軛)

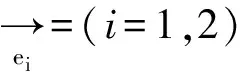
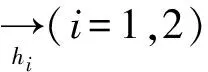
稱為Z的奇異值，且λ1≥λ2>0

對于任意的平面單色電磁波，取角頻率ω，波數為k，沿Z軸傳播，則在地面x-y平面內，一般產生橢圓極化。以電場矢量為例，數學表達式為式(8)。

(8)

其中：A為波的振幅；a為共同相位；φ為相對相位；

(9)

為了更方便地確定電磁波的極化狀態，我們引入復極化率P:

(10)

由式(9)可以令

a1=cosθ，a2=sinθ,θ∈[0,π]

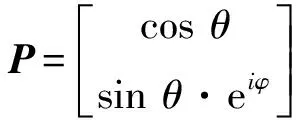
所以相應的電場向量與磁場向量對應形式為：

(11)

(12)

即

(13)

(14)

我們可以清晰觀察出[U]、[V]分別描述了電場與磁場的極化狀態，并且有兩個相互正交的主極化狀態。

依據上述的分解性質，將共同相位引入∧中并與[U]、[V]結合:

(15)

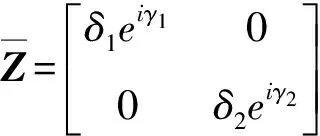
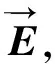
2 三維介質的阻抗張量的分析

2.1 三維介質阻抗張量的通用分析

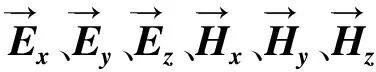
(16)

其中：α1、α2、β1、β2、γ1為對應分量的系數；它們可以通過電阻率ρ(Ω·m)與空間坐標(x，y，z)計算得出。

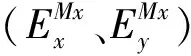
(17)

其中:α3、α4、β3、β4、γ2為對應分量的系數，它們可以通過電阻率ρ(Ω·m)與空間坐標(x，y，z)計算得出。將大地電磁場源分離成兩個相互正交的線性極化平面波, 場源Mx、場源My存在如下形式：

(18)

其中電場分量在水平方向的分量示意如圖2 所示。

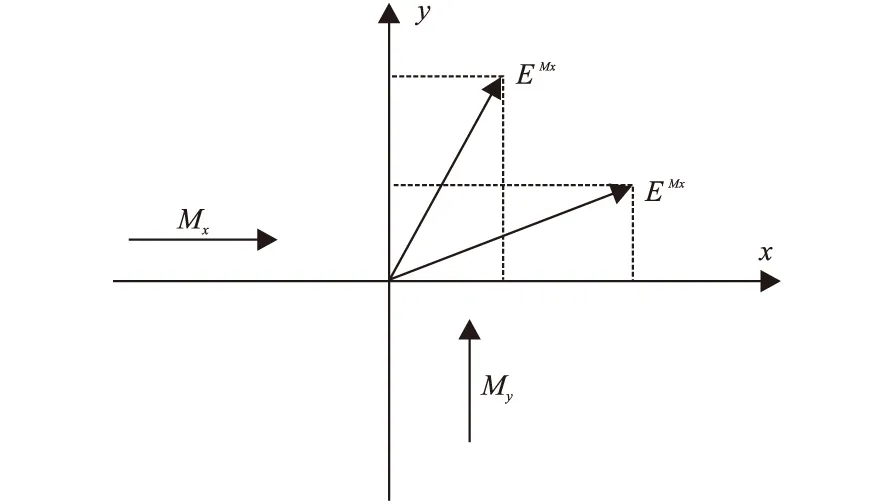
圖2 正交場源作用下電場分量在水平方向 的分量示意圖Fig.2 Component of the electric field component in the horizontal direction under the action of the orthogonal field source

根據場的疊加原理，對于一般垂直入射平面電磁波，各分量存在如下關系：

(19)

或表示為：

(20)

因為E=Z·H

(21)

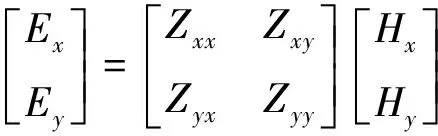
(22)

即

(23)

聯立式(14)、式(15)解方程組(23)，可得阻抗張量元素解

(24)

(25)

(26)

(27)

式(24)～式(27)為計算阻抗張量各元素的通用公式。 因此三維介質條件下，將場源M分解為電場形式或磁場形式代入即可獲得其值。綜上對于張量阻抗的計算，是不同場源在水平面上的分量疊加，將不同的場源分量帶入通用公式中可以計算出張量阻抗元素的值。

2.2 三維介質阻抗張量擴展

在三維介質的一般情況下，電場矢量存在:

(28)

(29)

(30)

k2=-iωμδ-ω2με

(31)

由式(28)～式(31)可知在三維條件下，電磁場的6個分量Ex、Ey、Ez、Hx、Hy、Hz全部耦合，不能解耦。

現推導出三維介質張量阻抗的形式，由方程可知，在三維介質中6個電磁場分量是相互耦合的，因此，提出如下三階阻抗張量形式：

(32)

由對張量阻抗的通用分析可知：

(33)

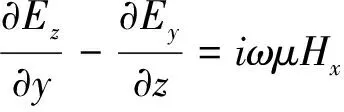
(34)

(35)

在實際的操作過程中可以獲得Ex、Ey、Hx、Hy、Hz這5個電磁場分量，結合式(35)計算出的電場垂直分量Ez，則電磁場的6個分量都成為已知。因此,可由電磁場分量求出阻抗張量各元素，由此可計算出相應的視電阻率以及相位特征。

Ex=ZxxHx+ZxyHy+ZxzHz

(36)

討論阻抗張量的計算方法。

若對某一頻率的電磁場作3次獨立觀測，則應有

(37)

式(37)中，上標表示對電磁場分量的觀測次數。

寫作矩陣形式：

(38)

式(38)可寫為

(39)

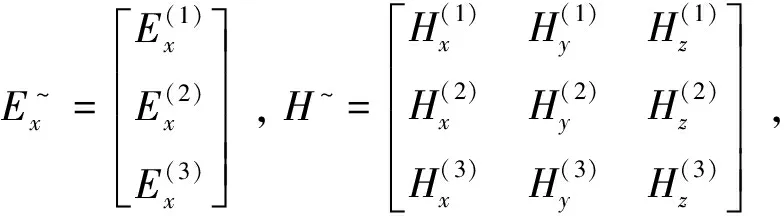
同理存在

因地下地質體的相應是非線性的，所以對式(39)有

因為|H～|≠0

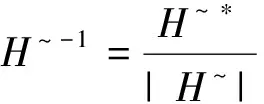
其中*表示伴隨矩陣。

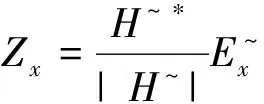
(40)

同理

(41)

(42)

綜上由式(40)～式(42)，將阻抗張量寫作：

(43)

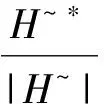
2.3 三維介質阻抗張量算法

為求阻抗張量計算方法，可采用算法(代數重構)進行反演計算。通過對給定初值進行計算，再將計算的結果與已知的數據求差，將差值以對應系數所占的權重進行分配，以上一次迭代結果相加，得到下一次的迭代值。

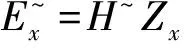
當滿足給定誤差時，停止迭代，輸出阻抗元素。獲得在三維介質中的阻抗張量元素值，由此給出了在無噪的情況下三維介質阻抗張量計算的具體方法。

但實際上不能直接這樣處理，因為實際觀測的數據存在噪音，僅從3組觀測數據來確定阻抗張量元素是不嚴謹的。為盡量減小噪音對數據質量的損壞，可以采用對大量觀測數據求平均值的方法，一般根據最小二乘原理求取阻抗張量元素的最佳估計值。

令

Exc=ZxxHx+ZxyHy+ZxzHz

(44)

其中:Hx、Hy、Hz為實測值；Exc為理論計算值，因觀測誤差與噪音的綜合影響，Exc并不等于實際觀測值，因此可以定義均方差函數

(45)

式中：*表示共軛復數；N為觀測次數(一般取3)。

將式(44)代入式(45)中得：

(46)

為使Ψ→min，則有

(47)

因為式(46)中Zxx、Zxy、Zxz均為復數，所以

iImZxy)Hyi+(ReZxz+(ReZxz+iImZxz)Hzi]}·

(48)

以Zxy為例，對其實部與虛部求偏導數，則有

(49)

(50)

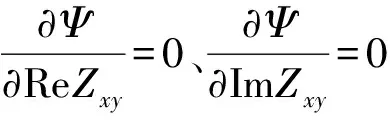
(51)

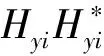
若用<>符號表示功率譜的平均值，則式(51)可表示為:

(52)

若對Zxx實部與虛部求偏導數，則有

(53)

若對Zxz實部與虛部求偏導數，則有

(54)

將(52)～(54)寫作矩陣形式

(55)

也可利用ART算法可以直接反演出阻抗張量。

同理可分析

Ey=ZyxHx+ZyyHy+ZyzHz

Ez=ZzxHx+ZzyHy+ZzzHz

的情況。

以上通過對已觀測的數據進行最小二乘處理以及求出觀測數據的功率譜平均值，可以得到如式(55)的矩陣形式，采用算法可以求解出阻抗張量元素的值。

3 結論

1)大地電磁測深法利用天然交變的平面電磁波為場源，依據在地表觀測到的包含地下地質體信息的電場值與磁場值計算出阻抗張量，并由阻抗張量計算出的視電阻率以及相位曲線特征來分析大地電性結構特征。 在 MT張量阻抗的分析中，對嚴格的二維介質可以進行旋轉分析以及正則分解，若要描述復雜的三維介質必須采用二維近似以及引入二維偏離度，其中正則分解可以描述主阻抗與電場與磁場的關系，可以確定地球的傳輸性質，較傳統的旋轉分析有了更明顯的地質含義。但自然界地下地質體是以三維形式出現，因此二維近似會產生偏差。而阻抗張量的通用分析則通過對場源的分解計算阻抗張量元素的值，可以直接對三維介質進行表述。

2)對于張量阻抗的分析中，對嚴格的二維介質可以進行旋轉分析以及正則分解，若要描述復雜的三維介質必須采用二維近似以及引入二維偏離度，其中正則分解可以描述主阻抗與電場與磁場的關系，可以確定地球的傳輸性質，較傳統的旋轉分析有了更明顯的地質含義。但自然界地下地質體是以三維形式出現，因此二維近似會產生偏差。而阻抗張量的通用分析則通過對場源的分解計算阻抗張量元素的值，可以直接對三維介質進行表述。

3)對三維介質阻抗張量的形式進行了更進一步的描述，采用了三階張量的形式表述阻抗，使得在形式上進行大地電磁測深時獲得的電場與磁場的關系統一，可以計算出三維介質的阻抗張量。

4)通過三維介質阻抗張量擴展中的分解方法，可以獲得阻抗張量的計算公式，對阻抗張量元素進行分部處理，結合觀測數據的功率譜平均值計算出功率譜矩陣，利用算法反演出對應的阻抗張元素值。

參考文獻：

[1] А.Н.Тихонв.Об определиии Электрических Характерстих Глубокихслоев Земной Коры，Докл.АН[J].СССР73，1950：295-297.

[2] CAGNIARD L．Basic theory of the magnetotelluric method of geophysical prospecting[J]．Geophysics，1953，18(3):605-635．

[3] SWIFT C W. A magnetotelluric investigation of an electrical conductivity in the south western united states[D].Cambridge:University of Cambridge，1967.

[4] E.YEE,K .V .PAULSON.The canonical decomposition and its relationship to the other forms of magnetotelluric impedance tensor analysis[J].Journal of Geophysics ，1987， 61(3):173-189.

[5] E.YEE,K.V .PAULSON.Canonical decomposition of the telluric transfer tensor[J].Journal of Geophysics，1987，61(3):190-199.

[6] 李偉.一種改進的阻抗張量分解方法及其應用[D].長沙：中南大學，2010.

LI W. An improved impedance tensor decomposition method and its application [D]. Changsha: Central South University, 2010. (In Chinese)

[7] 陳樂壽，王光鄂.大地電磁測深法[M].北京：地質出版社，1990.

CHEN L S, WANG G E. Magnetotelluric sounding method[M]. Beijing: Geological Publishing House, 1990. (In Chinese)

[8] 晉光文，孫杰，王繼軍.大地電磁(MT)阻抗張量的正則分解及其初步應用[J].地震地質，1998,20(3)：243-249.

JIN G W, SUN J, WANG J J. Magnetotelluric (MT) impedance tensor canonical decomposition and its preliminary application[J]. Seismology and geology, 1998,20 (3): 243-249. (In Chinese)

[9] 尹兵祥，王光鄂.大地電磁的阻抗張量正則分解的地質含義分析[J].地球物理學報,2001(3)：279-288.

YIN B X, WANG G E. Geological implication analysis of impedance tensor decomposition of magnetotelluric[J].Chinese Journal of Geophysics,2001(3):279-288.(In Chinese)

[10] 譚捍東，魏文博，鄧明,等. 大地電磁的張量阻抗通用計算公式[J].石油地球物理勘探,2004，39(1)：113-116.

TAN H D, WEI W B, WANG L, et al. Universal calculation formula of tensor impedance of magnetotelluric petroleum geophysical exploration[J].Oil geophysical prospecting,2004, 39 (1): 113-116.(In Chinese)