基于Rydberg原子的超寬頻帶射頻傳感器?

焦月春趙建明賈鎖堂

1)(量子光學與光量子器件國家重點實驗室,山西大學激光光譜研究所,太原 030006)

2)(山西大學極端光學協同創新中心,太原 030006)

1 引 言

電磁場強度與極化方向的精密測量在通訊、遙感、航空航天和雷達探測等方面具有重大的研究意義.傳統的測量通常采用偶極天線作為接收測量儀[1],但是測量前需要將偶極天線探頭放在一個標準電場中進行校準,而標準電場的測量又需要被校準過的探頭,因此這樣的校準沒有絕對固定的標準[2],會引入較大的校準誤差;并且當射頻電場的頻率較小時,所需要的探頭會非常龐大,導致探頭的靈敏度受到限制,且探頭一般為金屬,會對被測場產生干擾;傳統方法的最小測量值約為1 mV/cm,根據所測頻率的不同,其測量不確定度在4%—20%的范圍[3].現代技術中,人們通過光學手段將最小測量值降低到30μV/cm[4],靈敏度可達1 mV…cm?1…Hz?1/2[5],此方法主要受限于天線的轉換效率.人們也發展了其他的探測手段,例如基于光學非線性材料制作的探頭,但仍需要校準且會干擾待測電場.傳統射頻電場的測量精度和靈敏度已遠不能滿足目前科技和軍事需求的快速發展,因此迫切需要一種全新的測量方法來突破經典測量的限制.

近年來,利用原子本身性質的恒定不變性,將其作為多種測量標準,取得了巨大的研究進展.例如,原子鐘的測量精度優于10?17[6,7],基于原子的磁場測量儀可實現高靈敏度和高分辨率的磁場測量,靈敏度達到fTHz?1/2量級[8,9].利用Rydberg原子極化率大和能級間隔處于微波波段的特性,人們發展了一種基于原子能級的微波電場測量的新方法,基于原子的微波場測量具有非常重要的應用價值,并取得了快速的發展.文獻[10,11]綜述了基于Rydberg原子測量微波電場的研究進展,主要介紹頻率大于1 GHz微波場的測量方法,而對于頻率小于1 GHz的長波長射頻場的測量則需要采用完全不同的物理機制,本文重點介紹長波長射頻場的測量.

通過利用全光學的電磁感應透明(EIT)[12]探測微波場(>1 GHz)耦合形成的Autler-Townes(AT)分裂[13?25]和射頻場(<1 GHz)調制產生的AC Stark頻移[26]和射頻邊帶光譜[27?33],實現了超寬頻帶(0.01—1000 GHz)射頻電場的測量,理論上可探測的最小場強達100 nV/cm[14].這種測量方法無需校準[34],對被測電場無干擾且易于實現微型化和集成化[35].這里結合我們在射頻場測量方面的研究工作,對基于原子能級的免校準寬頻帶的電場測量方法進行較詳細的介紹,主要包括微波場測量原理簡介、長波長射頻場的強度、頻率和極化方向的測量原理和方法.

2 基于Rydberg原子的微波電場的測量(>1GHz)

Rydberg原子具有很大的極化率,相鄰Rydberg能級間隔處于微波波段,對應的微波躍遷偶極矩正比于主量子數n的2次方(～n2)[36].微波場耦合相鄰的Rydberg能級可產生微波A-T效應,利用Rydberg原子EIT測量微波A-T分裂實現微波電場的精密測量.

2.1 微波電場的測量及探測靈敏度的提高

基于Rydberg原子量子相干效應測量微波電場是一種全光學的方法,測量中不會對Rydberg原子產生破壞,具有探測速度快、可連續測量等優勢.早在1999年,人們就利用Rydberg原子實現了微弱靜電場的測量[37].2012年,Shaffer小組[14]利用微波耦合相鄰的兩個Rydberg能級,實現了基于Rydberg原子的微波電場測量,其測量的最小電場強度為8 μV/cm,靈敏度為30 μV…cm?1…Hz?1/2.相關的能級結構和實驗裝置如圖1所示,探測光和耦合光相對入射作用于一個裝有銣原子的熱蒸氣池中,當沒有微波電場作用時,可以觀測到如圖1(a)插圖上部分所示的標準階梯型三能級系統的EIT光譜,當施加與兩Rydberg能級共振作用的微波電場時,形成四能級系統,產生微波A-T分裂,進而形成如圖1(a)插圖下部分所示的EIT-AT光譜,分裂峰的大小?f對應于微波電場躍遷的Rabi頻率?MW,即

考慮多普勒修正因子,微波電場的幅值|E|表示為

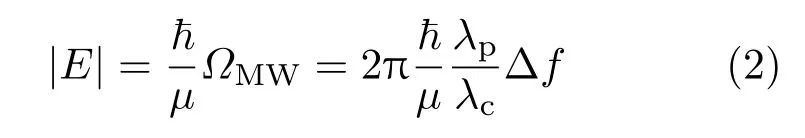
其中,μ表示微波電場耦合的兩個Rydberg能級的躍遷矩陣元,其不確定度在0.1%—1%范圍[38];λc和λp分別為耦合光和探測光的波長,其比值誤差約為10?8;～為普朗克常數.由測量的EIT-AT分裂獲得微波電場的強度,可探測的微波電場強度小于100 nV/cm.這一物理機理對于雙光子躍遷也同樣適用,這時微波電場導致的EIT分裂?f則與微波電場的振幅平方(|E|2)成正比[15,16].

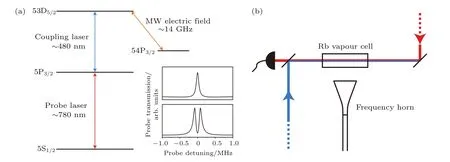
圖1 基于Rydberg原子量子相干效應測量微波電場的能級示意圖(a)和實驗裝置圖(b);圖(a)插圖中上曲線是沒有微波場作用時的三能級EIT光譜,下曲線是有微波場作用時的EIT-AT分裂光譜[14]Fig.1.The energy level diagram for the four-level system used for microwave(MW)measurements(a)and experimental set-up(b).Inset of(a):the top curve shows an EIT spectrum in the ladder three-level system without MW electric f i eld,the bottom is an EIT-AT spectrum with MW f i eld[14].

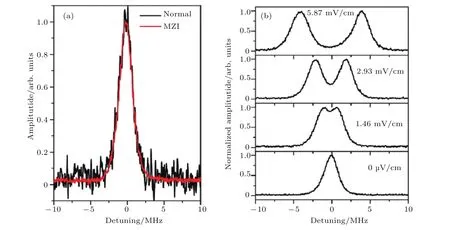
圖2 (a)普通探測和平衡零拍技術測量的EIT信號的比較;(b)微波場作用時,采用平衡零拍探測的不同微波場強的EIT-AT光譜[17]Fig.2.(a)Comparison of the Rydberg EIT signal with and without Mach-Zehnder interferometer(MZI);(b)measurements of A-T splitting spectra using the MZI for different RF electric f i eld amplitudes[17].

利用馬赫-曾德爾(MZ)干涉儀和平衡零拍探測技術測量探測光的正交相位分量,將測量的最小電場強度降低到1μV/cm,靈敏度提高到5 μV…cm?1…Hz?1/2[17], 如圖2 所示; 利用頻率調制光譜技術,進一步將測量靈敏度提高到3 μV…cm?1…Hz?1/2[18].

微波電場強度的測量不確定度和可測的最小空間分辨率同樣是微波測量的重要參數.Raithel小組[19]對基于Rydberg原子測量微波電場的不確定度進行了研究,指出當微波電場躍遷的Rabi頻率?MW大于兩倍的EIT譜線線寬時,測量的不確定度小于1%,并且實現了微波電場亞波長成像[20],對應的空間分辨率可達約100μm.隨后人們對微波場的極化方向進行了測量,測量精度可達0.5?[24].基于Rydberg原子EIT-AT測量微波電場的分辨率和極化方向的方法詳見綜述文獻[10].

2.2 寬頻帶微波電場的測量

傳統的微波測量方法,需要根據不同的頻段選取不同的天線探頭.基于Rydberg原子的測量是由微波耦合不同主量子數的Rydberg能級實現不同波段微波場的測量.通過Stark頻移改變兩個Rydberg能級間的能級差可以進一步擴展所測微波頻率的范圍.因此,選擇不同的Rydberg態即可實現頻率范圍在1—1000 GHz微波電場的連續測量.

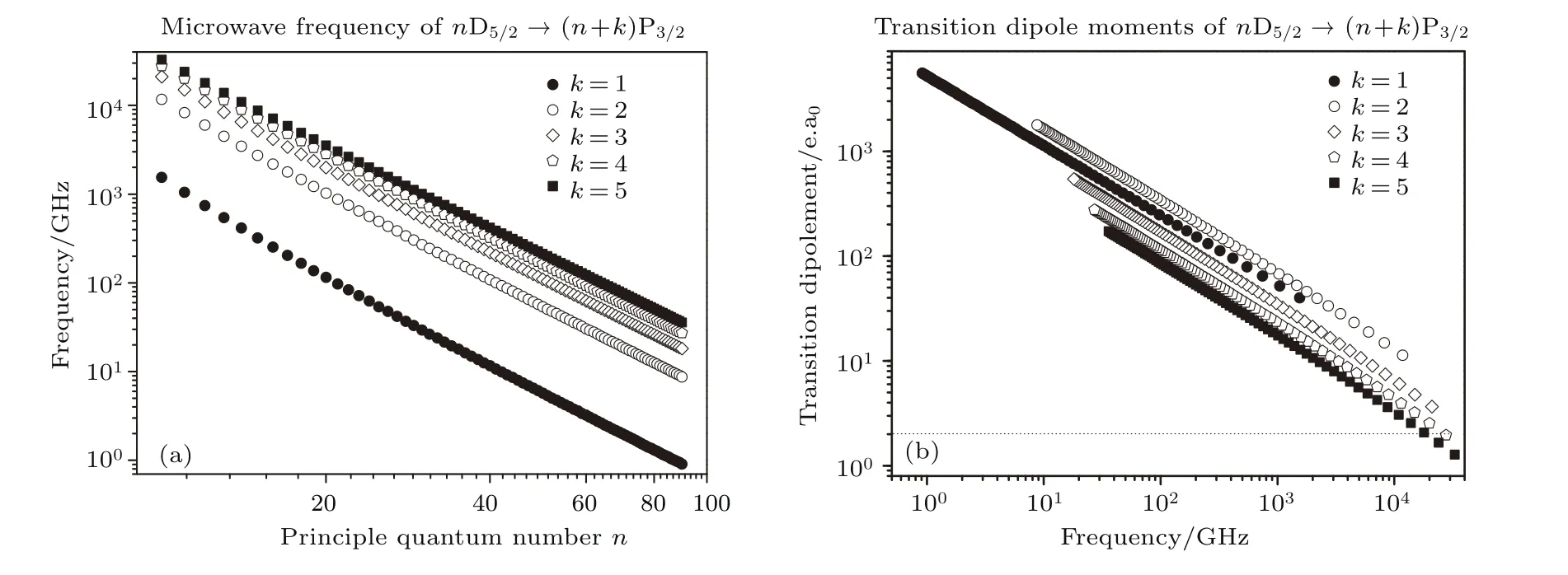
圖3 理論計算的不同主量子數n的銫Rydberg態對應nD5/2→(n+k)P3/2躍遷時的微波頻率(a)和相應的躍遷偶極矩(b)[11]Fig.3.(a)Calculations of the microwave frequency coupling the transition ofnD5/2→(n+k)P3/2as a function of the principal quantum numbern(a)and corresponding transition dipole moments(b)for Cs[11].

圖3(a)所示為理論計算的銫原子不同Rydberg態對應的耦合nD5/2—(n+k)P3/2躍遷時的微波頻率[11],其中k為整數.可以看出利用不同的Rydberg態可實現1—1000 GHz微波電場的測量,k>1時還可實現更高頻率微波場的測量.圖3(b)所示為相應的微波躍遷偶極矩.Rydberg原子具有豐富的能級結構,可以采用相鄰Rydberg原子的其他能級躍遷,或施加直流電場使Rydberg原子產生Stark頻移來調節Rydberg能級間的間隔以滿足所測微波頻率的要求.

目前實驗上已經實現了毫米波[21]及頻率大于200 GHz微波場[22]的測量,并且在Ka波段實現了對強微波電場頻率的連續測量,連續測量范圍達到±1 GHz[23].

3 基于Rydberg原子長波射頻場的測量(<1 GHz)

當被測射頻場的頻率小于1 GHz時,所需Rydberg能級很高,接近于原子的電離閾值且Rydberg能級非常密集,上述方法不再適用,此時需要采用射頻場調制Rydberg能級的方法進行測量.

3.1 射頻場強度和頻率的測量

在射頻場作用下,Rydberg能級會發生AC Stark頻移和射頻調制邊帶(Floquet能級),邊帶光譜線對射頻場的幅度和頻率都非常敏感,可以利用射頻場調制的RydbergEIT光譜實現射頻電場強度和頻率的精確測量.

Adams小組[27]于2010年利用EIT效應研究了長波射頻場調制的Rydberg原子光譜,觀察到Rydberg原子射頻EIT邊帶光譜.圖4(a)所示為相應的實驗裝置示意圖,探測光和耦合光相對入射作用于一個裝有銣或銫原子的熱蒸氣池中,射頻電場通過置于樣品池兩側的極板作用到原子上,通過探測透過的探測光可得到射頻EIT邊帶光譜;圖4(b)所示為射頻場調制的銣原子nS Rydberg態的能級示意圖,當沒有射頻電場作用時為標準的階梯型三能級系統,當施加射頻場作用時,在Rydberg能級兩邊出現一系列的邊帶能級,且能級間隔精確的等于所加射頻場的頻率.

圖4 (a)基于Rydberg原子量子相干效應測量長波射頻場的裝置示意圖,其中RF為射頻信號源,PD為光電探測器;(b)射頻場作用的銣原子nS Rydberg能級示意圖,Rydberg能級在射頻場中產生一系列的邊帶能級,能級間隔等于所加射頻場的頻率[27]Fig.4.(a)The schematic of the experimental setup for RF measurements,where RF is radio-frequency source,PD is photodiode detector;(b)the energy level scheme.An applied electric f i eld with angular frequencyωmgenerates a ladder Floquet state separated by integer multiples ofωm[27].

圖5為測量的射頻場作用下的Rydberg原子EIT光譜,圖5(a)為無射頻場時的EIT信號,圖5(b)為施加一個2π×26 MHz射頻場時觀測到的譜線,EIT主峰由于AC Stark效應產生頻移,同時在EIT主峰兩側的兩個對稱的小峰為射頻EIT邊帶光譜,由于躍遷選擇定則的限制,觀測到的邊帶譜線為2級邊帶,中心譜線與邊帶能級的間隔為所加射頻場頻率的2倍,即52 MHz.采用弱場作用下的微擾理論對實驗結果進行擬合,即可得到所加射頻場的大小.當施加一個DC偏置電場時,可觀測到1級邊帶的躍遷,如圖5(c)和圖5(d)中的小圓所示.隨后人們在小型化的空芯光纖中對射頻場綴飾的Rydberg原子光譜進行研究,實驗測量射頻場強度的不確定度小于4%,頻率測量范圍達到500 MHz[28].另外,人們還采用場電離的方法,對射頻場調制的鉀原子Rydberg光譜進行了研究[29].

在強射頻場作用下,Rydberg原子EIT譜線呈現出能級的交叉和避免交叉等更豐富的譜線特征[30,31],圖6(a)所示為在2π×70 MHz的射頻場作用下,觀測到的銫原子57S1/2Rydberg態的射頻EIT譜線隨所施加電場強度的變化,可以看到在弱場區域,EIT譜線只發生Stark頻移,隨著電場強度的增加,開始出現RF邊帶能級,到達強場區域后,由于57S1/2態原子與相鄰的多重態形成能級的避免交叉導致EIT的主峰強度逐漸減弱,當電場>2.7 V/cm時形成0級峰完全消失而邊帶峰增強的光譜結構,如圖中的數字1所示;在0級峰的正失諧區域,邊帶譜線表現出線性的平行光譜結構,如圖中的方形框所示.由理論計算與測量的譜線相比較,即可獲得待測射頻場的值.如圖6(b)所示,黑色的線表示電場強度為2.8 V/cm時的實驗結果,紅色的線為理論計算曲線,利用理論計算與實驗測量相比較,得到所施加的射頻場強度為2.8 V/cm,對應的測量不確定度小于3%.然而上述的測量方法都是根據譜線的特征與理論計算譜[16]相比較而得到射頻電場的大小,譜線本身沒有明確的校準點導致測量誤差偏大.

圖5 射頻電場作用下的EIT譜線 (a)無射頻場時的EIT信號;(b)—(d)2π×26 MHz射頻場中的EIT譜線;(c)和(d)中圓圈所示為施加一個DC偏置電場時,觀測到EIT光譜的1級邊帶[27]Fig.5.The effect of AC and DC electric f i elds on the Rydberg EIT spectrum.EIT spectra without a RF f i eld(a)and with a 2π×26 MHz RF f i eld(b),the circles in(c)and(d)denote the f i rst order side bands of EIT spectra as we apply a bias DC f i eld[27].

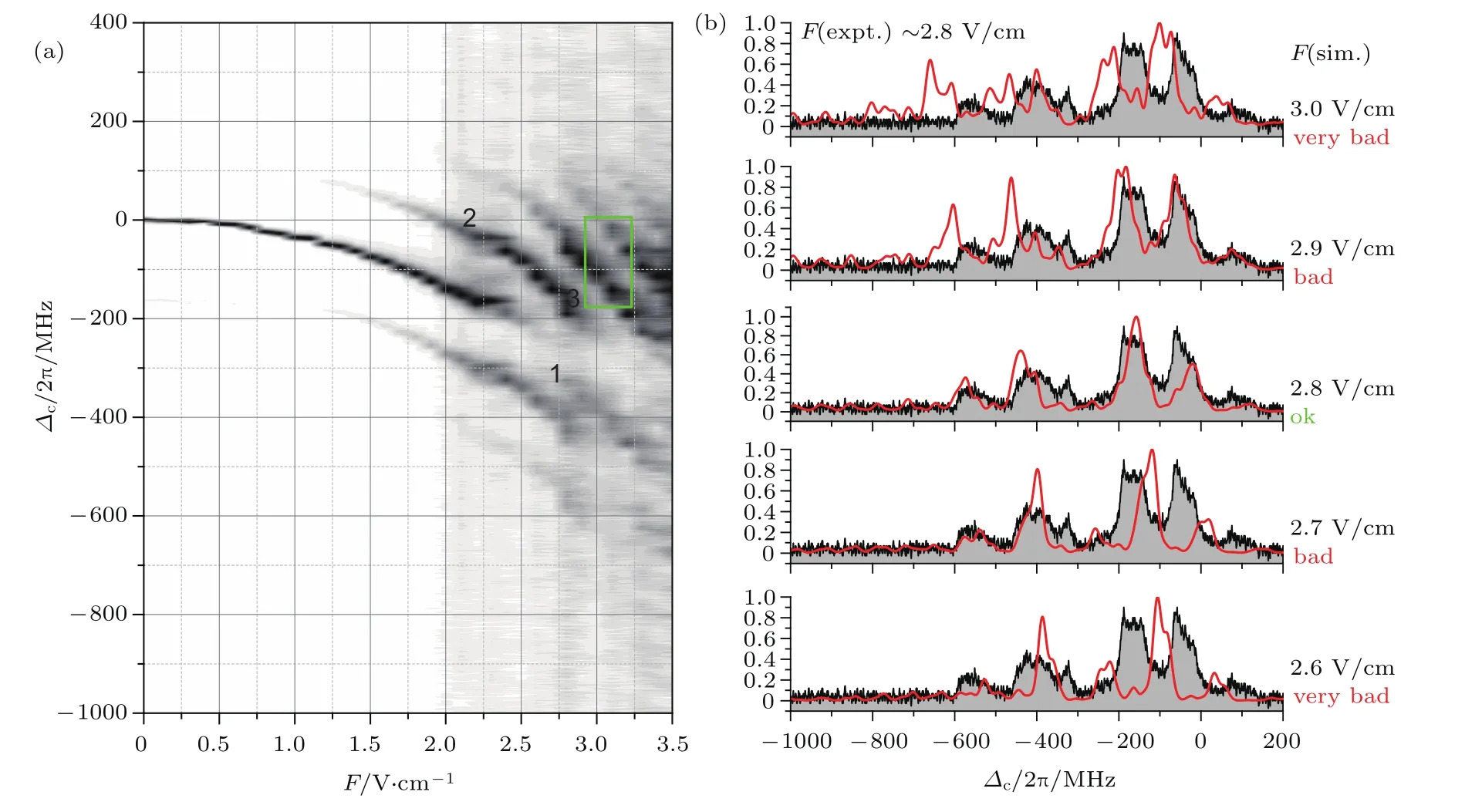
圖6 (a)射頻電場頻率為ωRF=2π×70 MHz時,測量的銫原子57S1/2態的EIT射頻邊帶譜線隨電場強度的變化,數字1—3表示形成避免交叉的位置,方形框表示正失諧處EIT光譜邊帶的平行結構部分;(b)由理論計算與實驗測量譜線的比較獲得射頻場強度E=2.8 V/cm[31]Fig.6.(a)Measurement of Rydberg excitation spectra as a function of RF electric-f i eld amplitude withωRF=2π×70 MHz,labels 1–3 indicate spectral features like avoided crossings,the square denote the linear spectra area;(b)comparison between the experimental spectrum with RF f i eld of 2.8 V/cm with the calculation for electric-f i eld values indicated on the right(red lines)[31].

nD態Rydberg原子的射頻光譜由于不同磁量子數的能級對應的極化率不同導致在電場中的頻移不同,頻移小的Stark能級與頻移大的Stark能級的射頻邊帶能級產生交叉,而相同的磁子能級形成邊帶光譜的避免交叉[32,33],這些能級的交叉或避免交叉可用于實現射頻電場的精確校準和測量.圖7右圖所示為射頻電場頻率為100 MHz時,測量的60D3/2,5/2態Rydberg原子射頻EIT光譜隨射頻電場強度的變化曲線,彩色的點為理論計算曲線,由于60D5/2,mj=5/2能級的極化率非常小,它的AC Stark頻移非常小,與極化率較大的mj=1/2,3/2的射頻邊帶能級形成很多的能級交叉(藍色方框所示),左圖為其中一個交叉點的放大,利用這些能級的交叉點作為射頻場強度測量的校準點,測量的不確定度小于1%,通過減小EIT譜線的線寬,理論上測量不確定度可以小于0.1%.另外,相同mj的射頻邊帶在特定電場處形成能級的避免交叉,如圖7中的兩位數字所示.這些避免交叉可用于進一步標定電場,減小測量的不確定度.

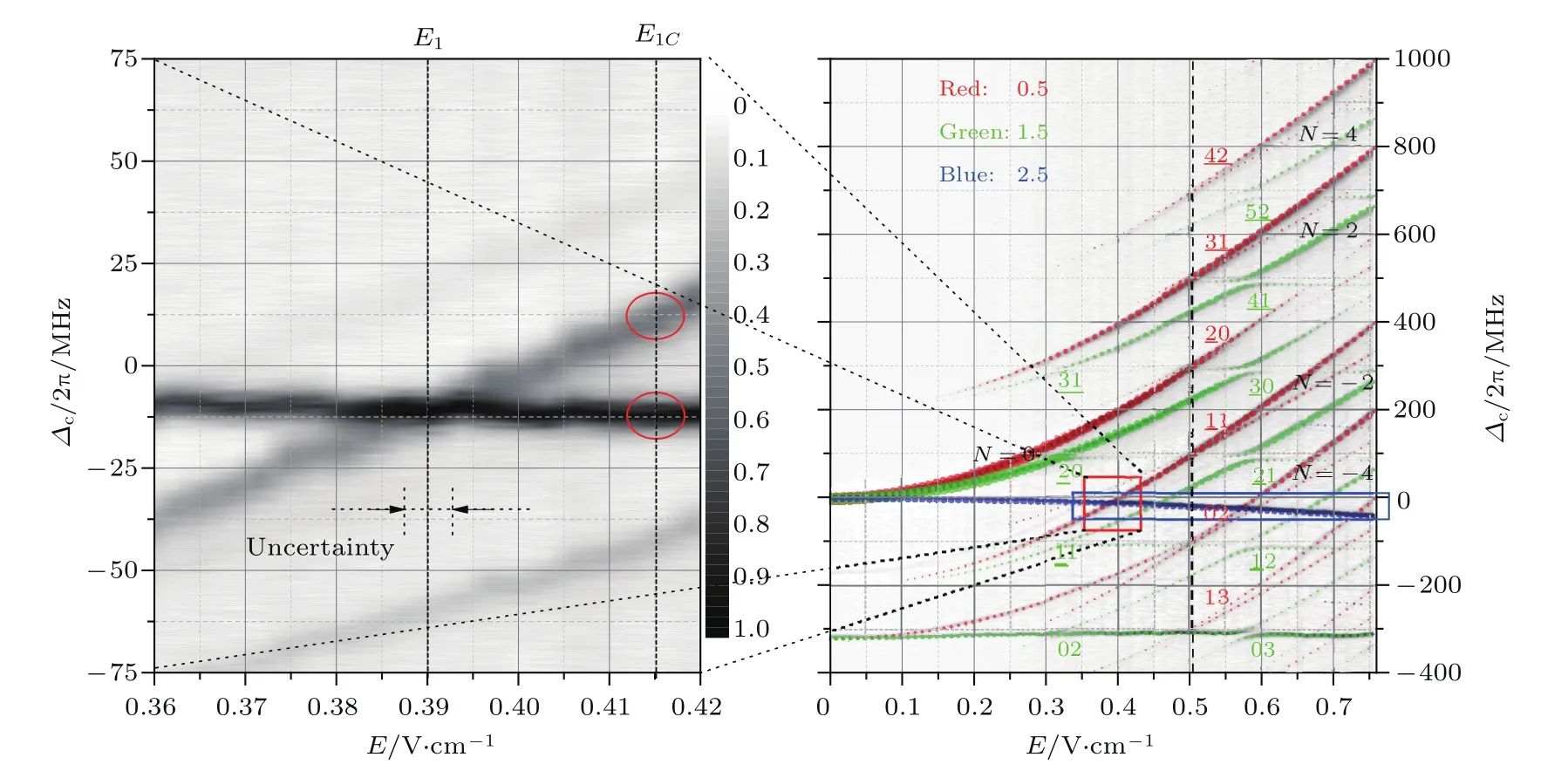
圖7 射頻電場頻率為ωRF=2π×100 MHz時,測量的60D3/2,5/2EIT射頻邊帶譜線隨電場強度的變化,彩色的圓點為理論計算的光譜線激發概率,圓點面積正比于激發概率,左圖為E1=0.390 V/cm處一個交叉點的放大[33]Fig.7.Measurement of Cs 60 DJFloquet map as a function of RF electric f i eld withωRF=2π×100 MHz with calculated Floquet maps displayed as overlaid semitransparent symbols,the area of the symbol is proportional to the excitation rate;the panel on the left shows an enlargement of the crossing atE1=0.390 V/cm,indicated by the red square[33].

3.2 射頻電場極化方向的測量

D態原子具有橢圓波函數,對電場的感應是各向異性的.RydbergnD態EIT射頻光譜的強度依賴于射頻場的極化方向,極化方向不同時對應同一譜線的激發強度不同,利用這一特點人們發展了基于nD態Rydberg原子測量射頻場極化方向的方法[33].

實驗上可以選取同一電場下的不同mj的兩條EIT譜線作為研究對象,由兩條譜線的相對強度隨電場極化方向的依賴關系可以對極化方向進行校準,即可通過所測兩譜線的相對強度獲知射頻電場的極化方向.這里選取圖7中交叉點后,電壓為E1C=0.415 V/cm時對應的J=5/2,mj=5/2的射頻0級邊帶和J=3/2,mj=1/2的N=2的邊帶為例加以說明.圖8中的插圖所示為θ=60?和θ=30?(θ為探測光和耦合光的極化方向與射頻電場的極化方向之間的夾角)時的射頻EIT光譜.標記A1的峰為J=5/2,mj=5/2的射頻0級邊帶,標記A2的峰為J=3/2,mj=1/2的二級射頻邊帶,A1和A2分別表示兩條譜線高斯擬合的面積,定義A=(A1?A2)/(A1+A2)表示這兩條光譜線的相對強度.圖8表示實驗測量和理論計算(實線)的相對強度與夾角θ的依賴關系,每一A值對應一個確定的電場極化方向.由Rydberg射頻EIT光譜即可測得待測射頻電場的極化方向,利用這種方法測量的射頻電場極化方向的精確度為2?—7?.

圖8 實驗測量的參數A=(A1?A2)/(A1+A2)與探測光和耦合光的極化方向與射頻電場的極化方向之間的夾角的依賴關系,實線為理論計算的結果;插圖為θ=60?和θ=30?時的EIT光譜,A1和A2表示所選兩條譜線的高斯擬合面積[33]Fig.8.Experimental data(symbols)and calculations(line)for the line-strength ratioA=(A1?A2)/(A1+A2)as a function of the polarization angleθ.Inset:measured EIT spectra forθ=60?andθ=30?,respectively.A1 andA2 denote the f i tted area of the EIT spectrum[33].

4 基于Rydberg原子射頻傳感器的應用和發展

如上所述,基于Rydberg原子的微波/射頻傳感器可實現自校準的超寬頻帶的微波、射頻電場強度和極化方向的精確測量,實現天線喇叭的精確校準,測量過程不會對被測場的分布產生影響;在Ku和K頻率波段微波電場的精確測量使其可以應用于軍事雷達和通訊衛星.基于Rydberg原子的場強傳感器可以在近場區域成像微波電場,易于實現探頭的微小型化,其測量的空間分辨率主要取決于激光束的腰斑大小和樣品池的尺寸,其測量的空間分辨率可達百微米量級,可以應用于很小的電路結構中測量電磁材料的特性,這些測量對于天線喇叭是難以實現的.基于原子的場傳感器對于電磁材料以及復雜的電子工業領域有重要的意義.

理論上,基于Rydberg原子的微波電場傳感器可測量的最小電場強度小于100 nV/cm,最高靈敏度可達到約pV…cm?1…Hz?1/2量級[11]. 基于原子的電場傳感器的測量靈敏度主要受到系統噪聲和雜散噪聲的限制以及原子之間的碰撞和測量蒸氣池形狀等的影響,人們已經采用多種實驗技術來提高系統的測量靈敏度.目前,利用頻率調制光譜技術、MZ干涉儀和平衡零拍探測技術使測量的最小電場強度為1μV/cm,最高靈敏度為3 μV…cm?1…Hz?1/2,遠高于傳統天線喇叭測量的結果.對于長波射頻場的測量,其測量不確定性主要受到譜線線寬的限制,理論上其測量不確定性小于0.1%.未來基于Rydberg原子的電場傳感器可能發展為第三類量子傳感器,可以克服量子噪聲的極限,大幅度的提高測量靈敏度.

5 總 結

本文介紹了基于原子的微波、射頻電場測量的最新研究進展,綜述了微波/射頻電場強度,極化方向的測量技術以及測量靈敏度.對于微波電場的測量,目前實驗上測量的最小電場強度為1μV/cm,最高靈敏度為3 μV…cm?1…Hz?1/2,遠高于傳統天線喇叭測量的結果;微波場極化方向的測量精度可以達到0.5?;通過選擇合適的Rydberg態,實現1—1000 GHz寬頻段的微波電場測量.對于小于1 GHz長波射頻場的測量,電場強度的測量不確定度可達0.1%,電場極化方向的測量不確定度為2?—7?.這種基于Rydberg原子能級參數進行電場測量的方法,利用原子能級實現自校準,不依賴外界參考,測量參數可以溯源到基本物理常量,并且測量方法對電場無干擾,易于實現微型化和集成化,具有廣泛的應用前景.

[1]Kanda M,Orr R D 1986IEEE Trans.Antenn.Propag.35 33

[2]Holloway C L,Gordon J A,Jefferts S,Schwarzkopf A,Anderson D A,Miller S A,Thaicharoen N,Raithel G 2014IEEE Trans.Antenn.Propag.62 6169

[3]Kanda M 1993IEEE Trans.Antenn.Propag.41 1349

[4]Sriram S,Kingsley S A,Boyd J T 1993US patent5 267 336[1993-11-30]

[5]Kanda M 1994IEEE Trans.Electromagn.Compat.36 261

[6]Hall J L 2006Rev.Mod.Phys.78 1279

[7]Bloom B J,Nicholson T L,Williams J R,Campbell S L,Bishof M,Zhang X,Zhang W,Bromley S L,Ye J 2014Nat.506 71

[8]Savukov I M,Seltzer S J,Romalis M V,Sauer K L 2005Phys.Rev.Lett.95 063004

[9]Patton B,Versolato O O,Hovde D C,Corsini E,Higbie J M,Budker D 2012Appl.Phys.Lett.101 083502

[10]Huang W,Liang Z T,Du Y X,Yan H,Zhu S L 2015Acta Phys.Sin.64 160702(in Chinese)[黃巍,梁振濤,杜炎雄,顏輝,朱詩亮2015物理學報64 160702]

[11]Fan H,Kumar S,Sedlacek J,Kubler H,Karimkash S,Shaffer J P 2015J.Phys.B:At.Mol.Opt.Phys.48 202001

[12]Mohapatra A K,Jackson T R,Adams C S 2007Phys.Rev.Lett.98 113003

[13]Zhang H,Zhang L,Wang L,Bao S,Zhao J,Jia S 2014Phys.Rev.A90 043849

[14]Sedlacek J A,Schwettmann A,Kübler H,L?w R,Pfau T,Shaffer J P 2012Nat.Phys.8 819

[15]Li J K,Yang W G,Song Z F,Zhang H,Zhang L J,Zhao J M,Jia S T 2015Acta Phys.Sin.64 163201(in Chinese)[李敬奎,楊文廣,宋振飛,張好,張臨杰,趙建明,賈鎖堂2015物理學報64 163201]

[16]Anderson D A,Schwarzkopf A,Miller S A,Thaicharoen N,Raithel G 2014Phys.Rev.A90 043419

[17]Kumar S,Fan H,Kübler H,Sheng J T,Shaffer J P 2017Sci.Rep.7 42981

[18]Kumar S,Fan H,Kübler H,Jahangiri A J,Shaffer J P 2017Opt.Exp.25 8625

[19]Holloway C L,Simons M T,Gordon J A,Dienstfrey A,Anderson D A,Raithe G 2017J.Appl.Phys.121 233106

[20]Holloway C L,Gordon J A,Schwarzkopf A,Anderson D A,Miller S A,Thaicharoen N,Raithel G 2014Appl.Phys.Lett.104 244102

[21]Gordon J A,Holloway C L,Schwarzkopf A,Anderson D A,Miller S A,Thaicharoen N,Raithel G 2014Appl.Phys.Lett.105 024104

[22]Simons M T,Gordon J A,Holloway C L,Anderson D A,Miller S A,Raithel G 2016Appl.Phys.Lett.108 174101

[23]Anderson D A,Raithel G 2017Appl.Phys.Lett.111 053504

[24]Sedlacek J,Schwettmann A,Kübler H,Shaffer J P 2013Phys.Rev.Lett.111 063001

[25]Fan H Q,Kumar S,Sheng J T,Shaffer J P 2015Phys.Rev.Appl.4 044015

[26]Zhu X B,Zhang H,Feng Z G,Zhang L J,Li C Y,Zhao J M,Jia S T 2010Acta Phys.Sin.59 2401(in Chinese)[朱興波,張好,馮志剛,張臨杰,李昌勇,趙建明,賈鎖堂2010物理學報59 2401]

[27]Bason M G,Tanasittikoso M,Sargsyan A,Mohapatra A K,Sarkisyan D,Potvliege R M,Adams C S 2010New J.Phys.12 065015

[28]Veit C,Epple G,Kübler H,Euser T G,Russell P St J,L?w R 2016J.Phys.B:At.Mol.Opt.Phys.49 134005

[29]Yoshida S,Reinhold C O,Burgd?rfer J,Ye S,Dunning F B 2012Phys.Rev.A86 043415

[30]Miller S A,Anderson D A,Raithel G 2016New J.Phys.18 053017

[31]Jiao Y C,Han X X,Yang Z W,Li J K,Raithel G,Zhao J M,Jia S T 2016Phys.Rev.A94 023832

[32]Yang Z W,Jiao Y C,Han X X,Zhao J M,Jia S T 2017Acta Phys.Sin.66 093202(in Chinese)[楊智偉,焦月春,韓小萱,趙建明,賈鎖堂2017物理學報66 093202]

[33]Jiao Y C,Hao L P,Han X X,Bai S Y,Raithel G,Zhao J M,Jia S T 2017Phys.Rev.Appl.8 014028

[34]Kitching J,Knappe S,Donley E A 2011IEEE Sens.J.11 1749

[35]Kübler H,Shaffer J P,Baluksian T,L?w R,Pfau T 2010Nat.Photon.4 112

[36]Gallagher T F 1994Rydberg Atoms(Cambridge:Cambridge University Press)pp38–49

[37]Osterwalder A,Merkt F 1999Phys.Rev.Lett.82 1831

[38]Mack M,Karlewski F,Hattermann H,Hockh S,Jessen F,Cano D,Fortagh J 2011Phys.Rev.A83 052515