蘇州地鐵客流波動特性分析

彭培培，楊越思，高國飛，魏 運，郭建華

?

蘇州地鐵客流波動特性分析

彭培培1，楊越思2，高國飛3，魏 運3，郭建華2

（1. 蘇州軌道交通集團有限公司，蘇州 215004；2. 東南大學智能運輸系統研究中心，南京 210096；3. 北京城建設計發展集團股份有限公司，北京 100037）

為研究軌道交通客流的波動性，提出使用SARIMA+GARCH這一隨機結構作為軌道交通客流的綜合時間序列模型。在這個隨機結構中，SARIMA模型描述客流時間序列的一階狀態，即均值特征；GARCH模型獲得客流時間序列的二階狀態，即條件異方差特征。采用蘇州地鐵全網客流數據作為分析實例，對5 min、15 min和1 h匯集度的工作日和休息日客流共6組客流數據進行波動性建模、預測與分析，結果表明，SARIMA+GARCH模型具有較好的預測性能。基于各組客流數據的分析結果，分別對工作日與休息日以及不同時間匯集度之間的客流波動特性進行對比，結果表明：休息日客流的波動性強于工作日客流；時間匯集度小的情況下，客流的波動性會更強。

城市軌道交通；客流波動性；SARIMA模型；GARCH模型

1 研究背景

乘客是軌道交通的服務對象，客流量和行為特性是決定軌道交通系統設計與運營的重要因素。在微觀層面，波動性是軌道交通客流的重要特性，主要包括平均水平變化特征和離散變化特征。平均水平變化特征表明平均客流率隨時間段的不同而不同；離散變化特征主要表達軌道交通客流的離散性或不確定性。以高峰小時客流為例，若高峰小時內客流率恒定在平均流率，則表明該時段內客流無離散現象，即客流沒有不確定的變化，是一個確定值。然而，實際客流始終處于變化之中，可能高于或低于平均流率，呈離散現象，具有不確定性。

客流的平均水平變化特征分析即客流的一階波動性分析，主要目的是分析客流平均值的演變特征，從而對客流平均值進行有效的預測。在交通流一階波動性研究領域，國內外的研究人員已經提出了諸多理論和方法，以實現連續交通流狀態的實時預測，主要包括歷史平均[1]、指數平滑[2]、時間序列方法（包括ARIMA模型、SARIMA模型等）[1，3]、譜分析方法[4]、神經網絡方法[5]、K-近鄰方法[6]、支持向量機方法[7]、卡爾曼濾波方法[8]、灰色預測方法[9]等，其中每一類預測方法又包含若干種預測模型。

由于地鐵客流具有隨機不確定性，為了便于決策者更好地做出決策，需要界定并充分表達這種離散特性，因此，在對客流平均水平變化特征進行分析的同時，應對客流的離散變化特征進行分析，即進行客流二階波動性的分析。在此基礎上，可對圍繞客流平均值的客流變化區間進行預測。與交通流一階波動性的研究相比，交通流二階波動性的研究還處在起步階段，常用方法主要有Bootstrap法[10]、GARCH法[11-12]和SV法[13]。

由于軌道交通客流具有明顯的周期性，而時間序列方法中的SARIMA模型適用于具有季節周期性的時間序列分析與建模；同時，GARCH模型能較好地處理非平穩及方差隨時間變化的時間序列問題，可以得到較為準確的預測區間，具有顯式結構，預測的實現過程依賴于完備的理論基礎。因此，本研究使用SARIMA+GARCH模型進行軌道交通客流的一階波性和二階波動性的分析，對客流的一階和二階波動性進行建模和預測，分析客流的一階和二階波動性在時間上的分布特征和規律。

2 地鐵客流波動特性分析方法

2.1 地鐵客流一階波動性建模及預測

客流一階波動性分析的主要研究對象為客流量的均值，處理客流時間序列的一階矩。

SARIMA模型的建模過程包括平穩性分析及白噪聲檢驗、模型的識別定階、模型的參數估計和模型的檢驗等步驟，在此基礎上，使用得到的SARIMA模型對擬合時間段內的客流量進行預測，得到客流量的預測值。SARIMA（，，）（，，）S模型擬合的表達式為：

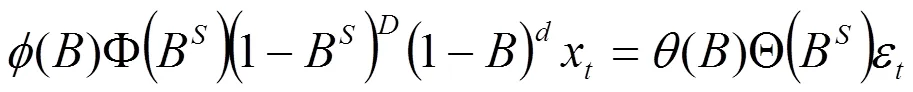
其中，為時間指數；為短時自回歸多項式的階數；為短時滑動平均多項式的階數；為短時差分的階數；為季節性自回歸多項式的階數；為季節性移動平均多項式的階數；為季節差分的階數；為延遲算子，比如Bx=x–1；(1–B)為季節差分；(1–)為短時差分；()=1–1–22–…–B為短時自回歸多項式；()=1–1–22–…–B為短時滑動平均多項式；

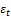
因此，地鐵客流一階波動性的建模及預測流程如圖1所示。

圖1 一階波動性建模及預測流程

2.2 地鐵客流二階波動性建模及預測

確定一階波動性的SARIMA模型后，可通過計算真實值與預測值之差得到模型的殘差序列，該殘差序列也為典型的時間序列。對殘差序列進行異方差性檢驗，若發現殘差平方具有高度相關性，則說明殘差序列具有ARCH效應，可對殘差序列擬合GARCH模型。

通過異方差檢驗后方可建立GARCH模型，一般情況下，簡單有效的GARCH（1，1）模型就足以描述大量的時間序列數據，于是在模型階數已定的情況下進行參數估計，這里采用最大似然估計。在確定的模型階數下，GARCH模型的建模步驟包括異方差性檢驗、模型識別、模型估計等。GARCH（1，1）模型擬合的表達式為：

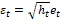
在此基礎上，使用得到的GARCH模型對擬合時間段內的客流條件方差進行預測，得到客流條件方差的預測值。由于預測受到其他各種隨機因素的干擾，預測結果具有一定的不確定性，即二階波動性。在這種情況下，為便于決策者更好地做出決策，應該更好地表達和體現這種不確定性。因此，在給出均值預測值的同時，計算一定置信水平下（一般選取95%）軌道交通客流的置信區間，研究其計算公式如下：

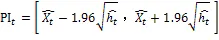
因此，地鐵客流二階波動性的建模及預測如圖2所示。

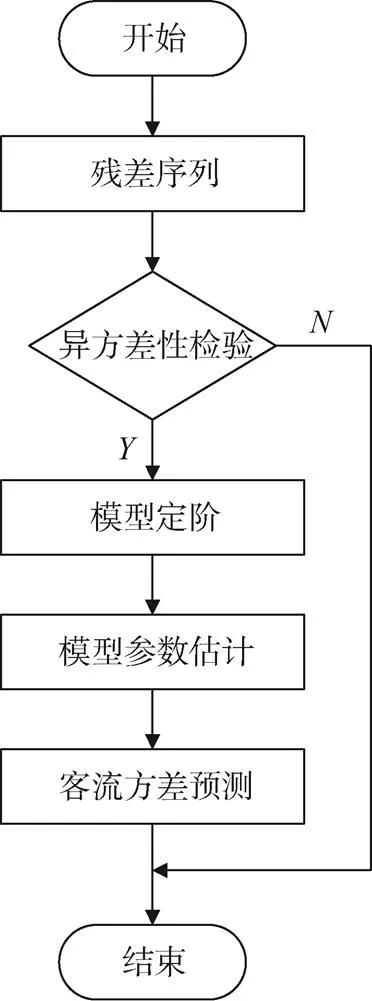
圖2 地鐵客流二階波動性建模及預測流程

2.3 地鐵客流波動特性分析與評價

選擇平均絕對誤差MAE和平均相對誤差MAPE作為一階波動模型性能評價的指標，MAE和MAPE的計算公式分別為

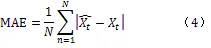
進行客流二階特征建模的目的是構建圍繞短時客流預測的預測區間，因此，通過對所構建的預測區間的優劣進行分析，以展示擬合模型的預測性能。無效覆蓋率（kickoff percentage，KP）指實際觀測值落入相應的預測區間外的百分比，若實際觀測值落在預測區間外，則定義該預測區間為無效預測，無效覆蓋率即為無效預測數占總體預測樣本數的百分比。根據此定義，其計算公式為

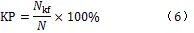
顧名思義，無效覆蓋率描述了預測區間覆蓋實際觀測值的能力，理想情況下，對于置信水平為95%的預測區間而言，其無效覆蓋率應當接近5%。

由于異方差性的存在，使用GARCH模型預測得到的二階波動值不是一個固定的值，而是一個變量，因此其預測95%置信區間寬度就會隨著時間點的不同而發生變化。從式（6）可以看出，當條件方差波動較大時，同樣置信水平下的預測區間變寬，反之預測區間變窄。而傳統的模型中假定方差為常數，即同樣置信水平下的預測區間寬度保持恒定。因此，異方差條件下，在給出圍繞軌道交通客流預測均值的預測區間時，采用寬度流量比（ratio of prediction interval to flow，）來評價預測區間的預測效果，將其定義為預測區間的寬度除以對應觀測值的均值水平。根據此定義，每一個預測區間都可以求到一個比值，以揭示預測區間的性能，其計算公式為

寬度流量比顯示了所構造預測區間寬度的合理性，為了更加精確地界定當前客流預測值的不確定性及客流波動性，應盡量得到較窄的預測區間。因此，寬度流量比接近于0時將會得到更為理想的預測結果。同時，寬度流量比的大小顯示了客流預測值不確定性及客流波動性的強弱。

3 蘇州地鐵客流波動特性建模和預測

對蘇州地鐵全網5 min、15 min和1 h匯集度的工作日和休息日進站客流共6組客流數據分別進行一階波動性建模、二階波動性建模，根據得到的模型進行客流均值和方差的預測，得到客流的預測值和預測區間。

5 min客流波動性研究選取的研究時間段為2016年4月1日至6月30日，將每日自6：00—23：30共210個5 min時間間隔的進站客流數據作為研究數據；15 min客流波動性研究選取的研究時間段為2016年1月1日至6月30日，將每日自6：00—23：00共68個15 min時間間隔的進站客流數據作為研究數據；1 h客流波動性研究選取的研究時間段為2015年7月1日至2016年6月30日，將每日自6：00—23：30共17個1 h時間間隔的進站客流數據作為研究數據。

3.1 一階波動性建模與分析

經平穩性分析、模型識別定階、模型參數估計、模型檢驗等步驟后，得到了各時間匯集度下工作日客流和休息日客流的一階波動性模型。由各匯集度下工作日和休息日客流擬合得到的SARIMA模型具有相同的階數，均為SARIMA（1，0，1）（0，1，1）S模型，其中，S為各時間匯集度所對應的周期。各時間匯集度下工作日和休息日客流SARIMA模型的表達式如表1所示。

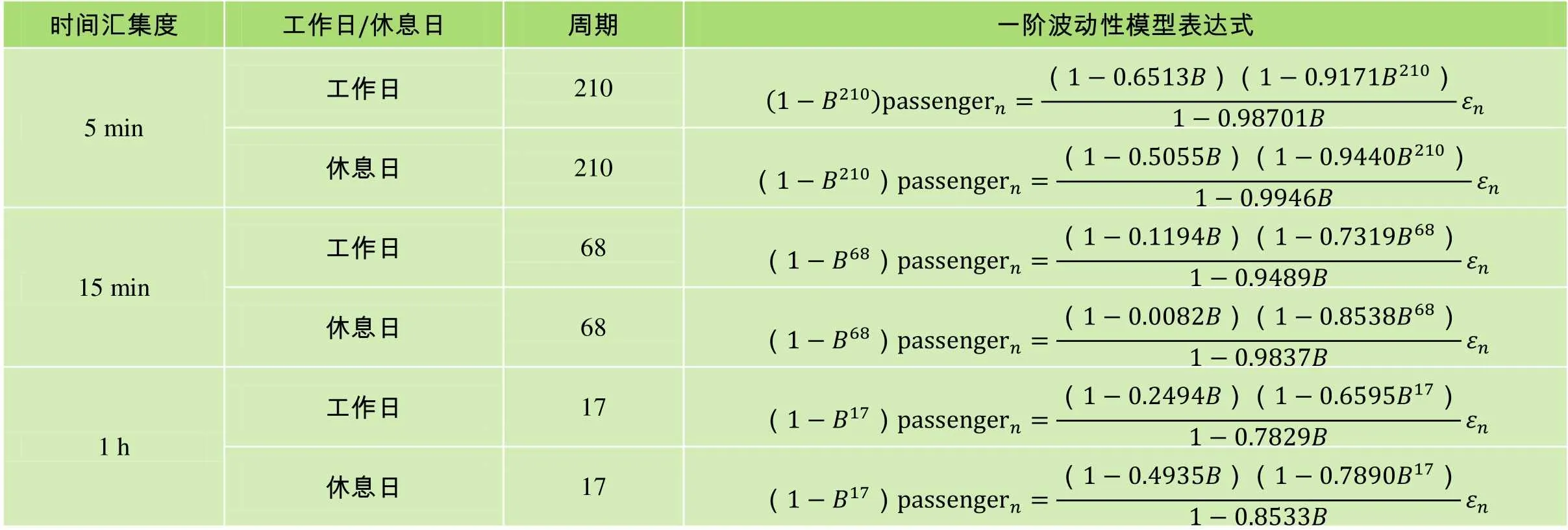
表1 一階波動性模型匯總

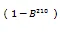
針對各匯集度下的工作日和休息日客流，使用得到的SARIMA模型對擬合時間段內對應的客流量進行預測。計算出各匯集度下工作日和休息日客流SARIMA模型的MAE和MAPE，匯總如表2所示。

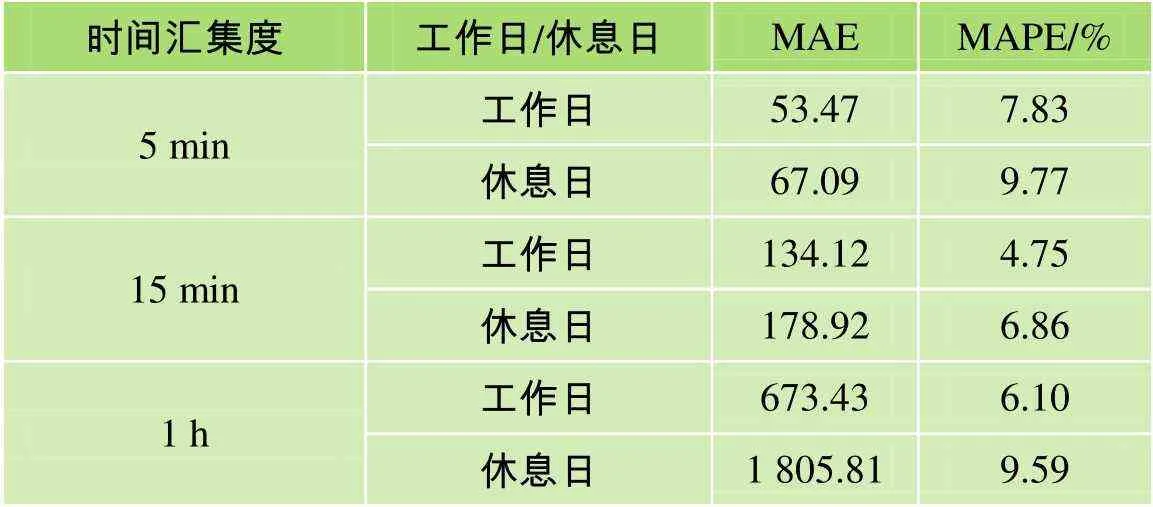
表2 平均絕對誤差、平均相對誤差匯總

可以看出，各匯集度下工作日和休息日客流預測值的平均相對誤差均小于10%，保持在較小的水平。因此說明，擬合得到的各SARIMA模型能夠較好地解釋各匯集度下工作日和休息日客流的一階波動特性。

MAE和MAPE的計算公式分別為

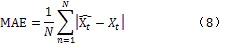
3.2 二階波動性建模與分析

采用GARCH（1，1）進行客流的二階波動性建模。經過異方差性檢驗、模型估計等步驟后，得到了各時間匯集度下工作日客流和休息日客流的二階波動性模型。由各匯集度下工作日和休息日客流擬合得到的GARCH（1，1）模型的表達式如表3所示。

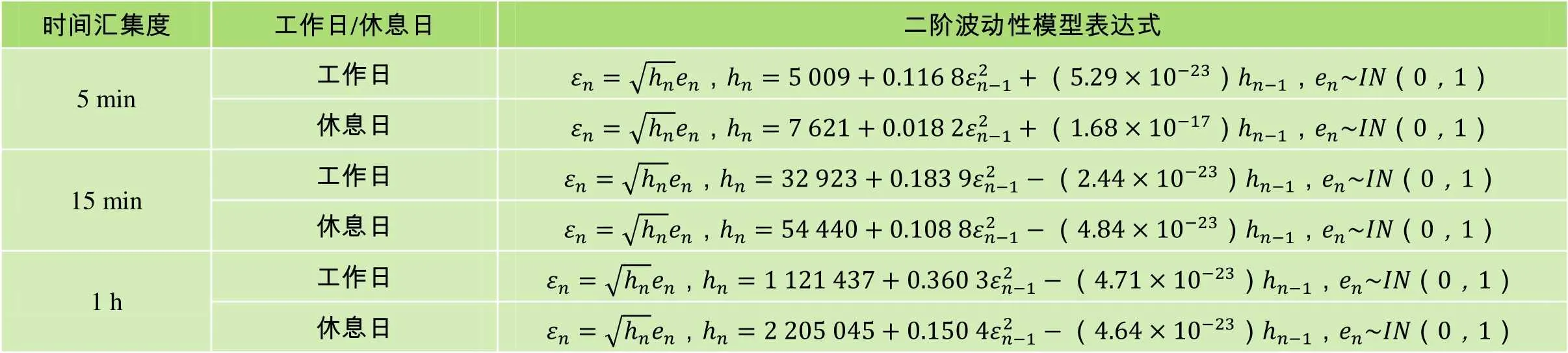
表3 二階波動性模型匯總

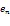
針對各匯集度下的工作日和休息日客流，使用得到的GARCH模型對擬合時間段內對應的客流方差進行預測。在客流預測值的基礎上，計算95%置信水平的客流預測區間。計算出各匯集度下工作日和休息日客流GARCH模型的無效覆蓋率（KP），匯總如表4所示。可以看出，各匯集度下工作日和休息日客流預測區間的無效覆蓋率均接近5％且保持在較低水平，符合95%置信水平的理想條件。因此說明，擬合得到的各GARCH模型在與各SARIMA模型的組合下，能夠較好地解釋各匯集度下工作日和休息日客流的二階波動特性。

表4 無效覆蓋率匯總

針對各匯集度下的工作日和休息日客流，計算所得到的各預測區間的寬度流量比。做出各自擬合時間段內最后5 d的寬度流量比與觀測值的對比圖，匯總如圖3所示（需要說明的是：為更清晰地顯示寬度流量比的變化趨勢，圖中所顯示寬度流量比的范圍為0～2，即寬度流量比大于2時會超出顯示范圍）。觀察圖3可發現，各對比圖呈現類似特點：每日大部分運營時段，在客流量明顯大于0的情況下，預測區間的寬度流量比保持在稍大于0的平穩狀態；而每日夜間接近于運營結束的一段時間內，隨著客流量接近于或等于0，預測區間的寬度流量比呈現增加趨勢。由于寬度流量比越小時預測結果越理想，所以，擬合得到的SARIMA + GARCH模型在客流量明顯大于0的情況下擁有更為理想的預測性能，而在客流量接近于或等于0的情況下會存在預測區間過寬的問題。但由于客流量在絕大多數時段都保持明顯大于0的狀態，因此，模型的預測性能在絕大多數時段都維持在較高水平。

3.3 客流波動特性對比分析與評價

3.3.1 工作日與休息日對比分析與評價

將工作日客流波動性的模型評價指標MAE（平均絕對誤差）、MAPE（平均相對誤差）及KP（無效覆蓋率）分別與休息日客流相應的指標進行對比，如表5所示。觀察該表可以看出，工作日的MAE、MAPE均小于休息日的相應指標值，故工作日客流的一階波動性預測精度比休息日更高；工作日的KP值均小于休息日的KP值，故工作日客流的二階波動性預測精度比休息日更高。

做出各匯集度下工作日與休息日客流日均寬度流量比的對比圖（在各對比圖中，5 min、15 min和1 h匯集度的工作日客流數據量分別與各匯集度下的休息日天數對應，選取各自研究時間段的最后28 d、58 d和114 d），匯總如圖4所示。觀察各對比圖可發現，各匯集度下，休息日的寬度流量比大于工作日的寬度流量比。因此，在5 min、15 min和1 h的匯集度下，休息日客流的波動性均強于工作日客流。這是因為：相比于工作日受到工作（上學）時間的約束，出行時間固定、各時段的客流量變化可能性小，休息日的時間安排則相對自由，從而各時段出行的客流量變化可能性相對較大，因此，反應在預測區間上，便表現為休息日客流的寬度流量比大于工作日客流的寬度流量比。

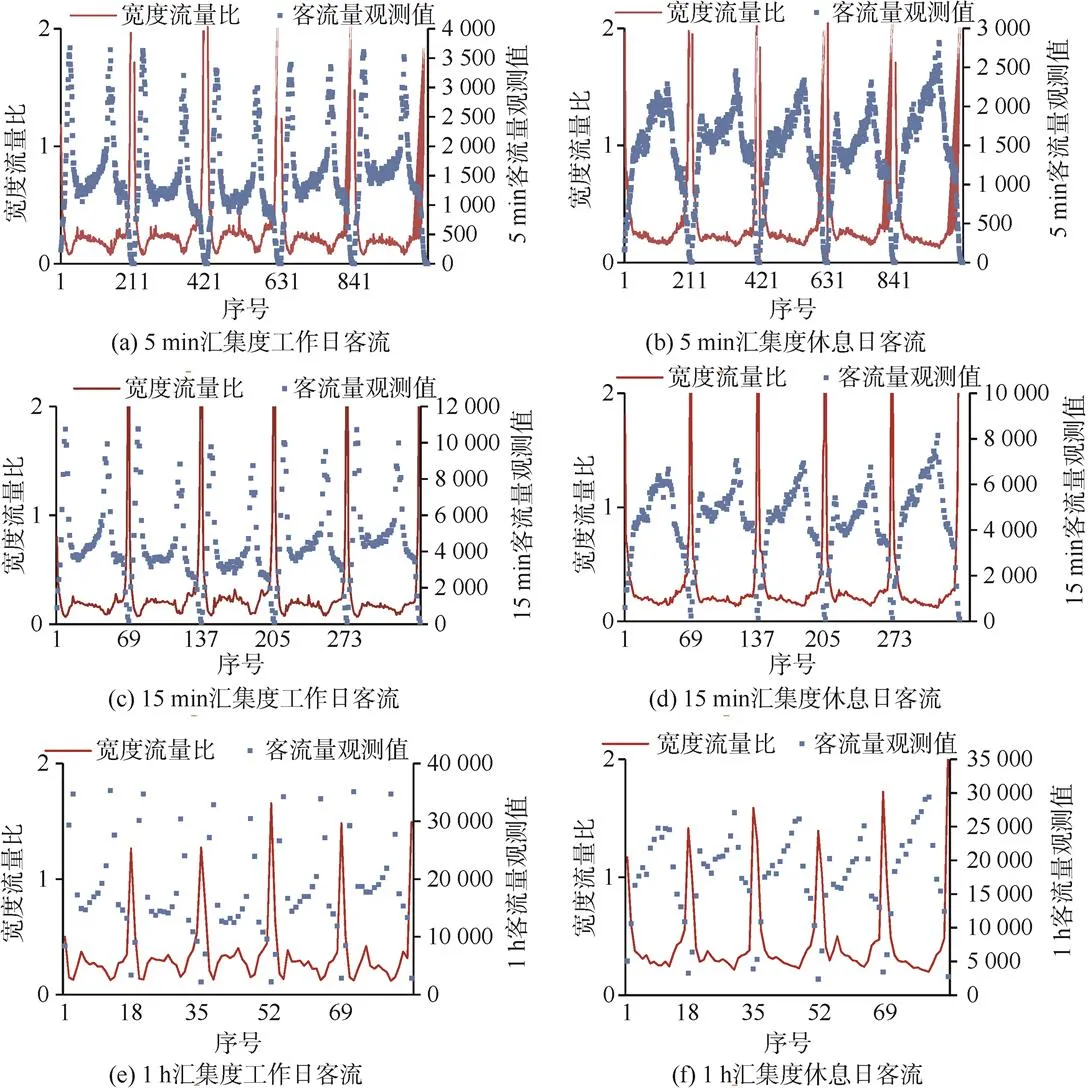
圖3 寬度流量比與觀測值對比圖匯總

表5 工作日與休息日模型評價指標對比

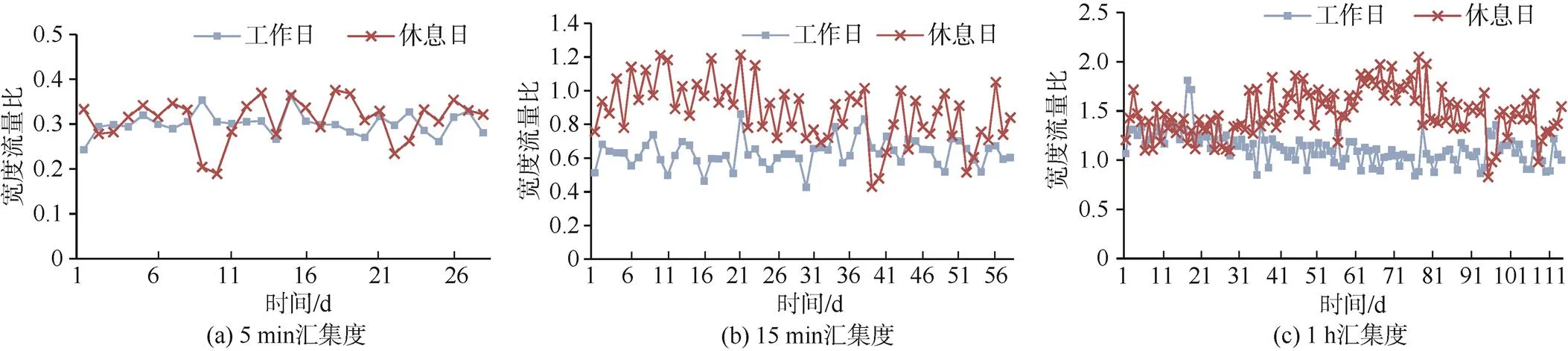
圖4 工作日與休息日寬度流量比對比圖匯總

3.3.2 不同匯集度對比分析與評價

將3種匯集度下客流波動性模型的評價指標MAPE（平均相對誤差）和KP（無效覆蓋率）分別進行對比，如表6所示。觀察該表可以看出，15 min匯集度下的MAPE值最小，5 min匯集度下的MAPE值最大，因此15 min匯集度下的客流一階波動性預測精度最高；5 min、15 min、1 h匯集度下的KP值呈現出遞減的趨勢，故1 h匯集度下客流的二階波動性預測精度最高。

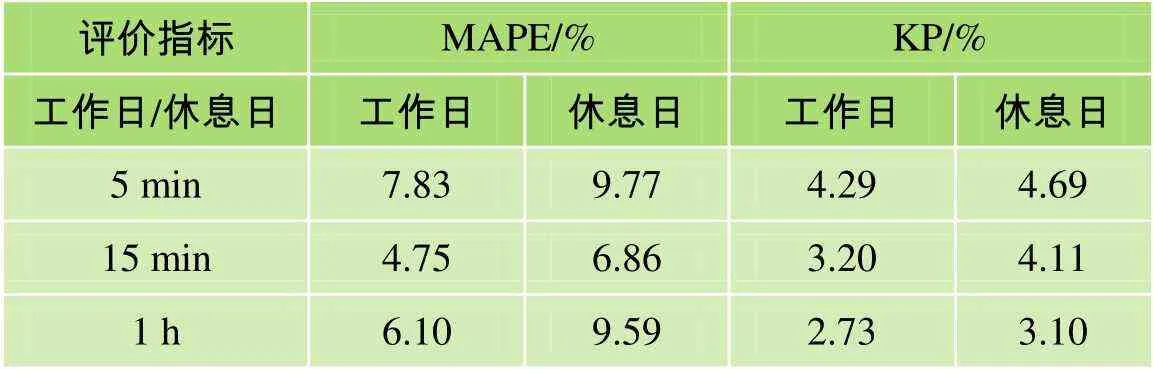
表6 不同匯集度下模型評價指標對比

針對工作日和休息日，分別作出各匯集度工作日客流日均寬度流量比的對比圖（選取2016年3月1日至2016年6月30日的預測結果），匯總如圖5所示。兩對比圖呈現出相同的特征：15 min和1 h匯集度客流日均寬度流量比較接近，1 h客流日均寬度流量比略小于15 min客流日均寬度流量比，二者均遠小于5 min客流日均寬度流量比，即5 min客流的波動性及不確定性最大。這說明：在時間匯集度小的情況下，各匯集間隔內的客流變化的可能性更大，而時間匯集度較大時，各匯集間隔內的客流相對穩定。

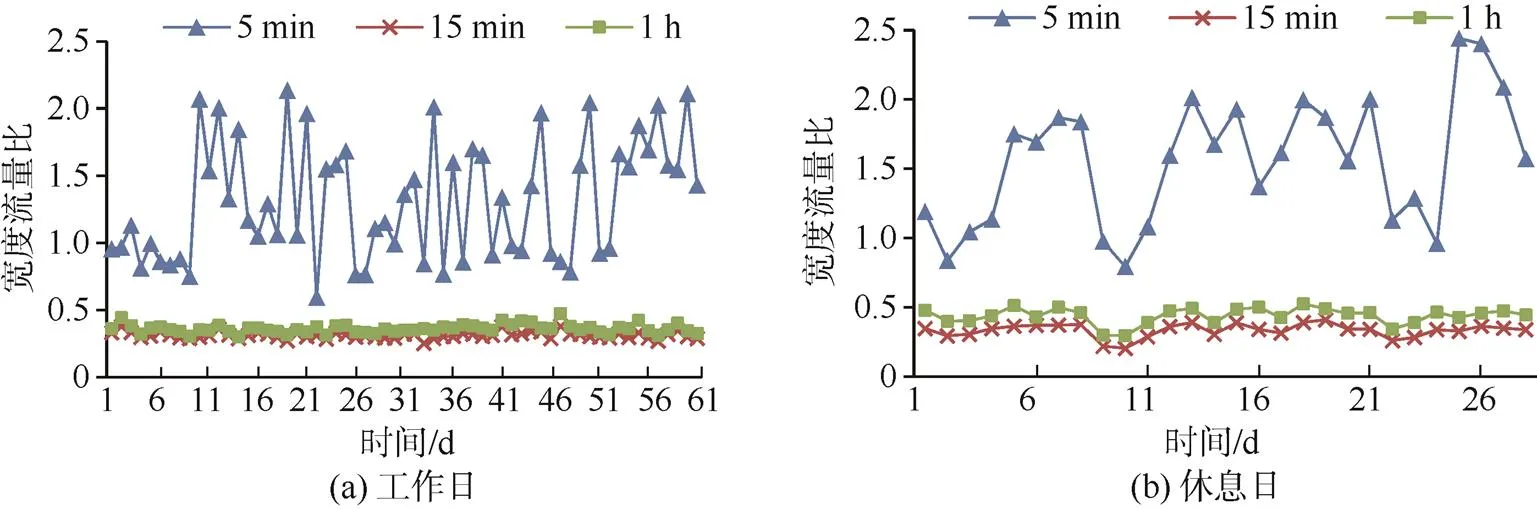
圖5 各匯集度客流日均寬度流量比對比圖匯總

4 總結

使用SARIMA +GARCH模型對蘇州地鐵5 min、15 min和1 h匯集度的工作日和休息日客流分別進行波動特性的建模和預測，并在此基礎上進行了客流波動性的分析和對比。建模和預測的結果表明：擬合得到的各SARIMA模型能夠較好地解釋各匯集度下工作日和休息日客流的一階波動特性；擬合得到的各GARCH模型在與各SARIMA模型的組合下，能夠較好地解釋各匯集度下工作日和休息日客流的二階波動特性；模型的預測性能在絕大多數時段都維持在較高水平。通過工作日與休息日的客流波動性對比發現：工作日客流的一階及二階波動性預測精度比休息日更高；休息日客流的波動性均強于工作日客流。通過各匯集度的客流波動性對比發現：15 min匯集度下的客流一階波動性預測精度最高、1 h匯集度下客流的二階波動性預測精度最高；在時間匯集度小的情況下，客流的波動性會更強，而時間匯集度較大時，客流的波動性相對較小。

[1] Stephanedes Y J, Michalopoulos P G, Plum R A. Improved estimation of traffic flow for real time control[J]. Transportation research record, journal of the transport-tation research board, 1981: 28-39.

[2] Ross P. Exponential filtering of traffic data[J]. Transpor-tation research record: journal of the transportation research board, 1982(869): 43-49.

[3] Ahmed M S, Cook A R, Analysis of freeway traffic time- series data by using Box-Jenkins techniques[J]. Transpor-tation research record: journal of the transportation research board, 1979(722): 1-9.

[4] Stathopoulos A, Karlaftis M G. A multivariate state space approach for urban traffic flow modeling and prediction[J]. Transportation research part C Emerging Technologies, 2003, 11(2): 121-135.

[5] Smith B L, Demetsky M J. Short-term traffic flow prediction: neural network approach[J]. Transportation research record: journal of the transportation research board, 1994 (1453): 98-104.

[6] 于濱, 鄔珊華, 王明華, 等. K近鄰短時交通流預測模型[J]. 交通運輸工程學報, 2012(2): 105-111.

YU Bin, WU Shanhua, WANG Minghua, et al. K-nearest neighbor model of short-term traffic flow forecast[J]. Journal of traffic and transportation engineering, 2012, 12(2): 105-111.

[7] Vanajakshi L, Rilett L R. A comparison of the perfor-mance of artificial neural networks and support vector machines for the prediction of traffic speed[C]// Intel-ligent Vehicles Symposium, IEEE, 2004: 194-199.

[8] Gazis D C, Knapp C H. On-line estimation of traffic densities from time-series of flow and speed data[J]. Transportation science, 1971, 5(3): 283-301.

[9] 張新天, 羅曉輝. 灰色理論與模型在交通量預測中的應用[J]. 公路, 2001(8): 4-7.

ZHANG Xintian, LUO Xiaohui. Application of gray theory and model in traffic flow forecast[J]. Highway, 2001(8): 4-7.

[10] Yang F, Yin Z, Liu H X, et al. Online recursive algo-rithm for short-term traffic prediction[J]. Transpor-tation research record: rournal of the rransportation research board, 2004 (1879): 1-8.

[11] Guo J, Williams B M. Real-time short-term traffic speed level forecasting and uncertainty quantification using layered Kalman filters[J]. Transportation research record: journal of the transportation research board, 2010 (2175): 28-37.

[12] Guo J, Huang W, Williams B M. Adaptive Kalman filter approach for stochastic short-term traffic flow rate pre-diction and uncertainty quantification[J]. Transporta-tion research part C: emerging technologies, 2014, 43: 50-64.

[13] Tsekeris T, Stathopoulos A. Short-term prediction of urban traffic variability: Stochastic volatility modeling approach[J]. ASCE journal of transportation engineering, 2010, 136(7): 606-613.

（編輯：郝京紅）

Characteristics of Passenger Flow Volatility of Suzhou Railway

PENG Peipei1, YANG Yuesi2, GAO Guofei3, WEI Yun3, GUO Jianhua2

(1. Suzhou Rail Transit Group Co., Ltd., Suzhou 215004; 2. Intelligent Transport System Research Center, Southeast University, Nanjing 210096; 3. Beijing Urban Construction Design & Development Group Co., Ltd., Beijing 100037)

To study the volatility of passenger flow, the random structure of the SARIMA + GARCH model as a compre-hensive time-series model for railway passenger flow is proposed. In this structure, the SARIMA model describes the first-order state, i.e. the mean feature, and the GARCH model obtains the second-order state, i.e. the conditional heteroskedasticity. Taking the passenger data of Suzhou railway as an example, the volatility of passenger flow in 5 min, 15 min, and 1 h time intervals and rest days is modeled, forecasted, and analyzed. It is found that the SARIMA + GARCH model can provide a good prediction performance. Based on the analysis results of each group, the passenger flow volatility between the working and rest days, as well as between different time intervals, is compared. The results show that the volatility of passenger flow on rest days is stronger than that on working days. At the same time, when the time interval is shorter, the volatility of passenger flow is stronger.

urban rail transit; passenger flow volatility; SARIMA model; GARCH model

U293.6

A

1672-6073(2018)02-0058-08

10.3969/j.issn.1672-6073.2018.02.010

2017-05-15

2017-06-05

彭培培，男，碩士，高級工程師，從事城市軌道交通前期研究和設計管理，464980255@qq.com

蘇州市軌道交通集團有限公司科研項目（SZZG06YJ 1050008）