基于多項式回歸的四帶圖像偏色校正算法①

曾兆濱, 鄭 華,2,3,4,5, 蔡堅勇,2,3,4,5, 廖曉東,2,3,4,5

1(福建師范大學 光電與信息工程學院,福州 350007)

2(福建師范大學 醫學光電科學與技術教育部重點實驗室,福州 350007)

3(福建師范大學 福建省光子技術重點實驗室,福州 350007)

4(福建師范大學 福建省光電傳感應用工程技術研究中心,福州 350007)

5(福建師范大學 智能光電系統工程研究中心,福州 350007)

1 引言

人類所能夠感知的光譜范圍大致為380 nm-780 nm,我們人眼的顏色感知主要是由物體的反射率決定的,在不同的光照條件下,物體的顏色在我們人眼看來是恒定不變的[1]. 這些特性對于感光元件CCD或CMOS而言是不存在的,它們所能夠感知的光譜范圍遠大于人眼,包括我們所熟知的紅外光. 感光元件獲得的圖像顏色是由光源、成像物體反射率和成像系統的光譜響應函數共同決定的,在不同光照條件下,感光元件所得到的物體圖像是不斷變化的,有時甚至失去了原本的色彩. 感光元件所獲取的圖像色彩與人眼所看到的顏色由于近紅外光的存在會產生偏色現象. 為了去除該偏色現象,尋找合適的顏色校正算法具有重要意義.

目前的偏色校正算法大多是針對RGB三帶圖像[2],而對于添加了近紅外光的RGB、IR四帶圖像并沒有通用的算法. 對于四帶圖像的校正問題,林李金等采用了基于RGB色彩空間進行顏色校正[3],即將偏色部分進行分區域校正,該方法缺陷在于對于每一幅圖都需要對偏色部分進行重新定位. 針對光譜串擾問題,Lei Li提出了利用解串擾矩陣的方式進行校正[4]. 實驗結果證明,該方法只需進行一次標定校正矩陣,就可以對同種光源條件下拍攝的不同圖像進行偏色校正.

2 構建解串擾矩陣

四帶圖像由于近紅外光的串擾,通過CCD或者CMOS等感光元件拍攝獲取的圖片會整體偏紅色,如圖1所示. 如何讓四帶圖像校正還原成標準三帶圖像,關鍵在于找到它們之間的映射關系,這需要精簡準確的數據擬合方法[5]. 本文通過分析測試感光元件中R、G、B三原色濾鏡的光譜串擾特性,在傳統多項式回歸的基礎上進行優化,構建光譜解串擾矩陣,可以實現在同種光源條件下矩陣的一次標定就能夠對不同圖像進行校正.

圖1 三帶圖像(左)與四帶圖像(右)

目前,市面上大多數彩色成像系統都是以RGB三原色為基礎. 對于CCD或CMOS感光元件而言,由于光照強度與光產生的電荷數量成正比關系,在輸出節點的電壓也與光強成正比[6]. 但是在電壓被量化的過程中,由于ADC需要對參考電壓進行選擇,使得原本的線性關系遭到破壞,量化輸出與光強呈現出增量線性關系[7].

2.1 線性回歸

如圖2所示,標準色卡上有24個色塊,分別獲取每個色塊的RGB三刺激值,三帶圖像(RGB圖像)第i個色塊三刺激值為Roi、Goi、Boi,而四帶圖像(RGBIR圖像)第i個色塊三刺激值記為Rci、Gci、Bci,其中i=1,2,3,…,24. 則：

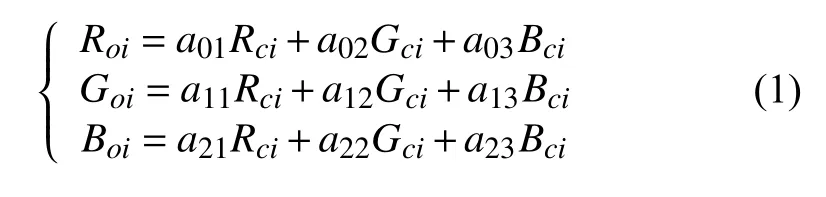
圖2 標準24色卡

記待校正的四帶圖像為矩陣Y,標準顏色的三帶圖像為矩陣X,紅外解串擾校正矩陣為M. 用矩陣方式從四帶圖像到三帶圖像顏色值得變換可以表示為：

其中,

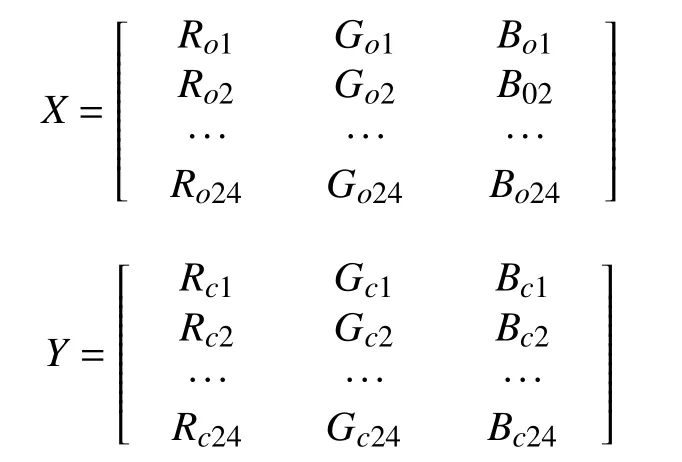
矩陣M可由最小二乘法優化得到[8],M即為所求的解串擾矩陣.

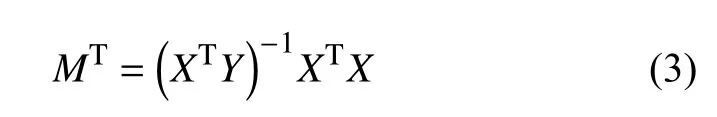
將所求的矩陣M帶入公式(2),即可得到消除紅外串擾后圖像的三刺激值. 該算法的關鍵之處在于要設計合理的多項式系數.

2.2 增量線性回歸

由于圖像在經過感光元件的處理后,量化輸出與光強呈現出增量線性關系,并且四帶圖像比較特殊,因為紅外光會對原本的R、G、B三通道造成不同程度的干擾,并且這種干擾在不同強度的紅外光條件下是不一樣的. 因此,本文在公式(1)的基礎上稍作修改,即在公式(1)等式右端添加常數項b,以此來修正成像系統在轉換過程中所帶來的增量偏差.即：

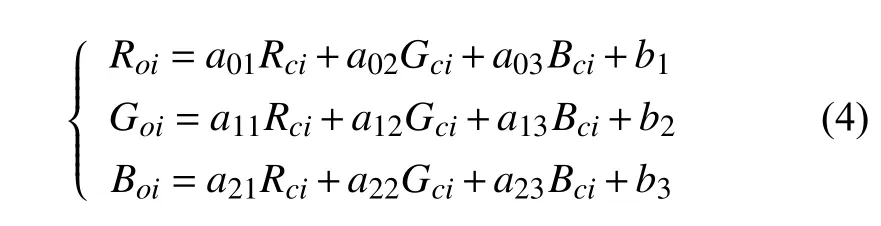
相應的,矩陣Y也添加一列常數1：

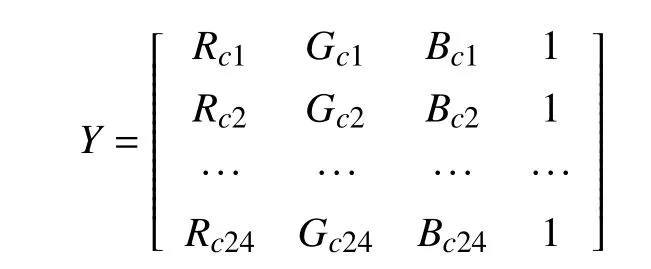
矩陣M維數變為3×4：

矩陣X則保持不變.則解串擾矩陣系數a的求解方法等同于線性回歸中解串擾矩陣M的求解方法.

3 四帶圖像偏色校正

實驗裝置系統如圖3所示,在傳統的CMOS攝像頭鏡頭前面稍作修改,即使紅外濾光片可手動調節,并且外加一片可見光+850 nm雙峰濾光片,以此來濾除除850 nm以外的大部分紅外光. 該實驗采用海洋光學USB4000微型光纖光譜儀測定850 nm雙峰濾光片的光譜特性曲線,采用標準光源對色燈箱來獲取D65光源,采用850 nmLED燈陣列來獲取近紅外串擾光,采用愛色麗標準24色卡來獲取校正矩陣數值. 整個數據處理過程都在MATLAB R2012a平臺上.

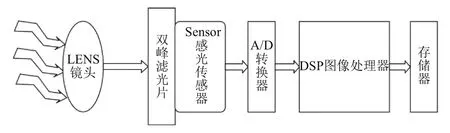
圖3 攝像頭模組結構框圖

3.1 解串擾矩陣數值校正

首先,光源條件為D65+850 nm,在攝像頭去除紅外濾鏡和不去除紅外濾鏡兩種情況下,對圖2所示的標準色卡的24個色塊分別獲取R、G、B三個分量的平均值. 其次,對獲取的24個色塊中的隨機20個色塊(例如除編號7,12,18,23以外的20個色塊)的R、G、B分量進行校正矩陣的獲取.

記在D65+850 nm光源且有紅外濾鏡條件下測量得到的色塊RGB三刺激值為矩陣Y’,在D65+850 nm光源且沒有紅外濾鏡條件下測量得到的色塊RGB三刺激值為矩陣X’,校正矩陣為M’,算法流程圖如圖4所示. 則校正算法過程可表示為：

通過算法獲得的校正矩陣為：

然后將之前獲取的編號為7,12,18,23的色塊RGB信息進行矩陣構建,結果如下.

四帶偏色情況下四個色塊RGB信息的矩陣為：

三帶標準情況下四個色塊RGB信息的矩陣為：

通過算法獲得的校正矩陣M’和Y1帶入公式(5)得算法獲得的矩陣X(算法)為：

對于矩陣X(算法)和矩陣X1數值上來看,校正效果較好.

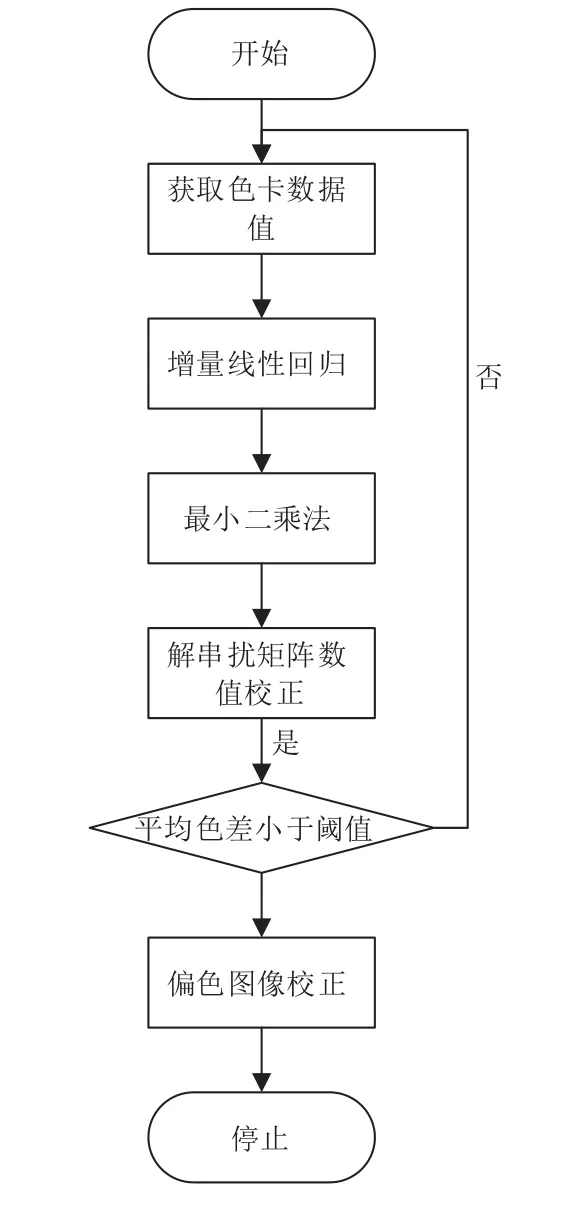
圖4 四帶圖像偏色校正流程

3.2 偏色圖像校正

通過本文3.1節獲取的解串擾矩陣M,對此光源條件下整幅圖像進行校正,結果如圖7.在同種光源條件下,利用該矩陣對不同景物進行四帶圖像的校正,結果如圖10和圖13.

圖5 D65+850 nm有紅外濾鏡(色卡)

圖6 D65+850 nm無紅外濾鏡(色卡)

圖7 通過校正矩陣獲得的圖片(色卡)

圖8 D65+850 nm有紅外濾鏡(盆栽1)

圖9 D65+850 nm無紅外濾鏡(盆栽1)

圖10 通過算法獲得的圖片(盆栽1)

圖11 D65+850 nm有紅外濾鏡(盆栽2)

圖12 D65+850 nm無紅外濾鏡(盆栽2)

圖13 通過算法獲得的圖片(盆栽2)

4 實驗結果與分析

本文所采用的系統為改造后的CMOS攝像頭. 標準比色卡由24個不同色塊構成,光源條件為色溫6500 K外加850 nm紅外光,為避免陰影和形狀的影響,在拍攝過程中,應保持色板的平穩. 按本文所提的算法進行四帶圖像的校正,并采用顏色空間的兩點間距離來表示色差實驗結果見圖14,其中圖(a),(b),(c)的縱坐標分別表示R、G、B三個分量在校正前后與標準三帶圖像情況下的差值,圖(d)的縱坐標則表示三刺激值在校正前后與標準三帶圖像情況下的色差值,4幅圖的橫坐標都表示24色塊的編號.實驗結果表明,校正前四帶圖像中色塊的R、G、B三個分量與三帶圖像差值較大,而經過本文算法校正后圖像中色塊的R、G、B三個分量與三帶圖像差值較小,算術平均值整體趨近于0,證明該算法適用于四帶圖像的偏色校正. 某些色塊的校正情況改善并不明顯,可能是由于色塊擺放位置或者是鏡頭獲取的色卡圖像像素偏差所引起的. 在同一光源條件下,利用同一個解串擾矩陣對不同景物進行校正,也呈現出較好的校正效果. 因此,本文的算法適用于四帶圖像的偏色情況,并且能夠在進行一次標定解串擾矩陣的情況下就可以對同種光源條件下拍攝的不同圖像進行偏色校正,恢復圖像自然的色彩.

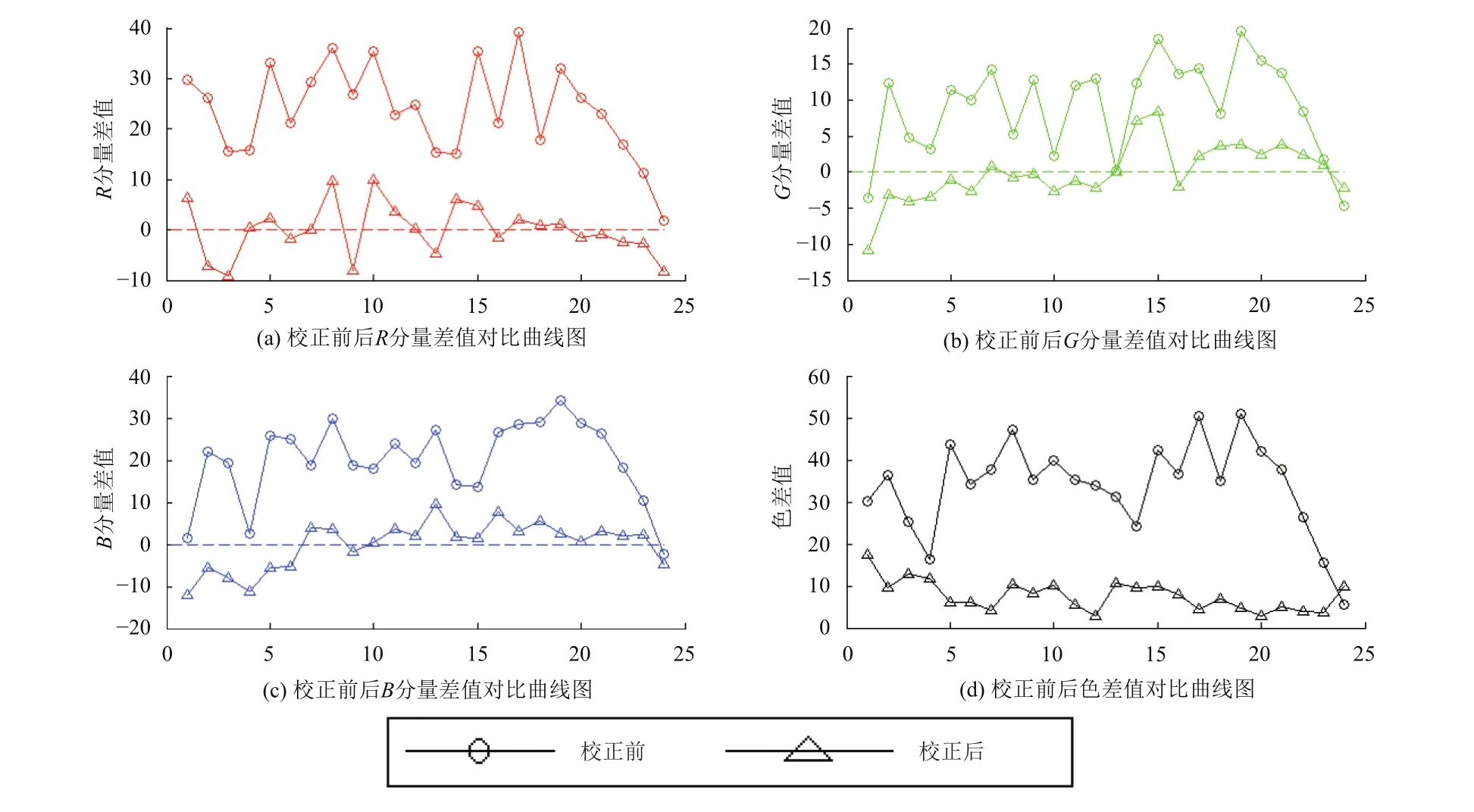
圖14 校正前后RGB三分量差值和色差對比曲線圖

5 結論與展望

本文提出了一種基于多項式回歸思想的四帶圖像偏色校正算法,該算法是在同種光源條件下,巧妙的稍改攝像頭模組,對校正前后的兩幅圖像,從標準24色卡的各個色塊中獲取數據. 根據四帶圖像的特點,構建出合適的校正矩陣,利用最小二乘法解出解串擾矩陣的各個系數,將該解串擾矩陣對四帶圖像進行偏色校正,并且在同種光源條件下對不同景物的四帶圖像進行校正. 實驗結果表明,由于在有850 nm雙峰濾波片情況下,近紅外光對圖像的影響并不會很大,根據本文的算法進行校正可以大致的還原出原有的色彩,達到了較好的校正效果. 對于今后多帶圖像校正情況的研究具有一定的參考價值.

1 Lukac R. Single-sensor imaging：methods and applications for digital cameras. Boca Raton：CRC Press,2008. 267-294.

2 王歡,陳向寧,姜明勇. 偏色圖像的色彩還原算法實現. 四川兵工學報,2012,33(3)：109-111.

3 林李金,蔡堅勇,蔡榮太,等. 基于RGB色彩空間的四帶樹木圖像顏色校正方法. 計算機系統應用,2014,23(4)：154-158.

4 Li L,Speed TP. An estimate of the crosstalk matrix in fourdye fluorescence-based DNA sequencing. Electrophoresis,1999,20(7)：1433-1442. [doi：10.1002/(ISSN)1522-2683]

5 臧留琴,張鎮西,苗寶剛,等. 多重定量PCR系統中多色熒光檢測和光譜串擾校正方法. 光學學報,2014,34(1)：0117002.

6 Healey G,Kondepudy R. Radiometric CCD camera calibration and noise estimation. IEEE Transactions on Pattern Analysis and Machine Intelligence,1994,16(3)：267-276.[doi：10.1109/34.276126]

7 白雪生,劉立峰,徐光祐,等. 基于顏色圖直方圖的監督顏色恒常性算法. 清華大學學報(自然科學版),1997,37(3)：1-6.

8劉關松,呂嘉雯,徐建國,等. 監督顏色校正方法研究. 計算機學報,2003,26(4)：502-506.