小波閾值改進算法的遙感圖像去噪

陳竹安,胡志峰

(1. 東華理工大學測繪工程學院，江西 南昌 330013；2. 流域生態與地理環境監測國家測繪地理信息局重點實驗室，江西 南昌 330013； 3. 江西省數字國土重點實驗室，江西 南昌 330013； 4. 江西生態文明建設制度研究中心，江西 南昌 330013)

在利用傳感器采集和接收地物信息的過程中，難免會受到外界及傳感器自身存在的噪聲的影響，從而使圖像的信息模糊、邊緣缺失等。為了能實現對遙感影像圖的邊緣信息化，以及圖像分割、圖像分類等后續工作的準確進行，噪聲的消除起到了重要的作用。隨著技術的發展，對于圖像質量成品的提高，如傳統的均值濾波、中值濾波、維納濾波及Gaussian濾波都已經漸漸失去了主要的地位。自從Dono-ho對基于小波閾值去噪方法進行了一系列的理論研究[1]，提出了小波去噪的軟、硬閾值方案開始，很多國內外學者開始在此基礎上進行相應閾值函數的改進。有對硬閾值函數、軟閾值函數或半軟閾值函數的改進，以及閾值函數與一些其他變化(如PCA,NSCT等)的結合。這些改進方法在圖像處理及信號處理去噪方面都起到了很大的改善作用。

針對當前研究的現狀及專家學者研究的理論，本文通過在硬閾值、軟閾值相互衍生的折中閾值函數基礎上結合軟閾值函數進行綜合改進，該改進方法利用了可變的參數，可以通過對參數的調整來調節函數的處理效果。通過多種方法的Matlab仿真試驗比較及評價指標來驗證該方法的精度和效果。

1 小波閾值圖像去噪算法

1.1 小波閾值圖像去噪的原理

小波去噪的原理是充分利用小波分解噪聲后，有效的信號在小波的變換后小波系數會比噪聲經過小波分解的系數要大[2]。在此基礎上可以選擇一個合適的閾值來判斷該系數是由噪聲引起還是由有效圖像信號引起的。最后選擇一個更加合理的閾值分解小波系數來達到去噪的目的。遙感圖像去噪也是如此。

假設一個大小為M×N的遙感數字圖像f(j,k)，在遙感圖像上加一個服從(0，δ2)的高斯白噪聲。f(j,k)表示從F(j,k)中恢復的原始圖像:F(j,k)=f(j,k)+r(j,k)。r(j,k)表示圖像所加的高斯噪聲。

1.2 閾值函數

在小波閾值去噪的函數中，基于傳統的閾值函數，硬閾值、軟閾值函數的基礎上有關學者提出了半軟閾值，以及這種閾值等新的閾值函數。

硬閾值函數表達式為

(1)

軟閾值函數表達式為

(2)

小波閾值的提出即是基于式(1)和式(2)兩種基礎的閾值函數。其中，yjk為輸出后的小波系數；xjk為帶有噪聲的小波系數；t為圖像的閾值；sign(xjk)為符號函數。由于基礎的硬閾值函數和軟閾值函數存在處理的缺陷，硬閾值函數不連續容易造成小波重構的吉布斯現象，軟閾值雖然克服了這一缺陷，但是存在過于平滑失真的現象。因此通過傳統的硬閾值和軟閾值函數相繼推出相關的折中閾值函數和半軟閾值函數。在去噪的處理上可以起到結合的效果。

半軟閾值函數表達式[3]為

(3)

折中閾值函數表達式為

(4)

半軟值函數折中閾值函數結合了硬閾值函數與軟閾值函數的特點。從折中閾值函數調整系數a可以看出，當a=1時為軟閾值函數，a=0時為硬閾值函數，其中a∈[0 1]半軟閾值函數在軟閾值的基礎上通過閾值選取兩個閾值作為門限分別為t、t0。這樣可以保證小波系數的穩定性和效果性相對更加明顯。基于上述幾個函數的表達式及性能的穩定性，本文改進閾值函數表達式(1)如下

(5)

該閾值函數不僅結合了半軟閾值和折中閾值函數的優點，也進一步提高了去噪的效果。在改進的閾值函數中采用同半軟閾值函數的上下閾值法則，加入了可調整系數a。其中改進的閾值函數中下閾值定義為t0=sigma·t，sigma也作為可調整系數，該閾值函數中sigma∈[0 1]，該閾值函數通過對于小波系數的判斷從3個區間內進行閾值函數處理，在選擇過程中也更加全面。但是通過試驗表明此函數在處理噪聲的情況下并不優于前面4種閾值函數。

本文閾值函數表達式為

(6)

通過對于基本的一些閾值函數方法的推導，以及添加可變參數k放入改進的閾值函數中。通過試驗及文獻[4]設定其中k∈[0 3]的正整數。取該區間的系數值可對噪聲有較好的處理效果。

1.3 閾值的選擇

在小波域閾值函數去噪方法中，閾值的選擇是對于小波閾值函數處理一個非常關鍵的問題[5]，如果閾值選擇不恰當，當選擇的閾值太低圖像中仍會含有大量噪聲，不能達到去噪的效果，閾值選擇過大又會造成圖像中地物信息的缺失，使圖像信息變得過度平滑。在現今的閾值方法中有固定閾值(VisuShrink閾值)、基于Stein的無偏似然估計原理的自適應閾值(SureShrink閾值)、GCV閾值和BayesShrink閾值等[6]。本文選擇的閾值方法為固定閾值方法，即

(7)

式中，t為圖像閾值；δ為噪聲的標準差；s(1)·s(2)為圖像的大小M×N。δ=median(sjk)/0.674 5，通過固定閾值法選取可靠的閾值參數，實現圖像更好地去噪。

2 本文算法的實現步驟

新構造的小波閾值去噪函數，在處理的試驗過程中分為4大步驟：

(1) 選取大小為M×N的試驗圖像，加入均值為0，方差為20的高斯白噪聲，加入噪聲后利用小波變換進行小波分解，本文將小波分為3層，采用的小波為db8，分解得到小波高頻和低頻的信號，得到相應的小波系數xjk。

(2) 運用閾值方法(即固定閾值方法)進行閾值的選擇，計算出合理的閾值解。

(3) 選擇合適的閾值后，進行閾值函數的處理，對步驟(1)中分解小波系數進行閾值處理得到相應的輸出小波系數yjk，使得小波的系數yjk-fjk的差值極限趨近為零(fjk為原圖像的小波系數)，將得到閾值后的小波系數進行重構，得出去噪后的圖像。

(4) 進行質量評價，運用峰值信噪比(PSNR)、標準均方差(MSE)、均方根誤差(RMSE)及信噪(SNR)比來評價去噪圖像的質量[7-10]。

3 仿真試驗及評價質量

3.1 評價質量

本文運用的評價指標，即小波閾值去噪常用的評價指標，能有效直觀地判斷去噪后圖像的改善標準[11]。

標準均方差為

(8)

峰值信噪比為

PSNR=10·lg(MAX2/MSE)

(9)

式(8)中，fjk、yjk分別為圖像的純凈系數、小波處理后的系數。式(9)中MAX為圖像的灰度最大值(即255)，在評價中MSE越小，PSNR越大，說明去噪效果更好[12]。

在用固定閾值法選定閾值后，為了比較硬閾值、軟閾值、半軟閾值、折中閾值及新構建的閾值函數在圖像去噪中處理的精度，通過Matlab仿真處理進行了兩個試驗的對比。

3.2 試 驗

3.2.1 試驗1

為了檢測該新構建的閾值函數標準化，在處理遙感影像圖之前，先用構建函數對標準的圖像檢測試驗圖Lean圖像進行試驗認證及對比本次的試驗(其中調整參數a=0.1，sigma=0.4,k=1。)如表1和圖1所示。

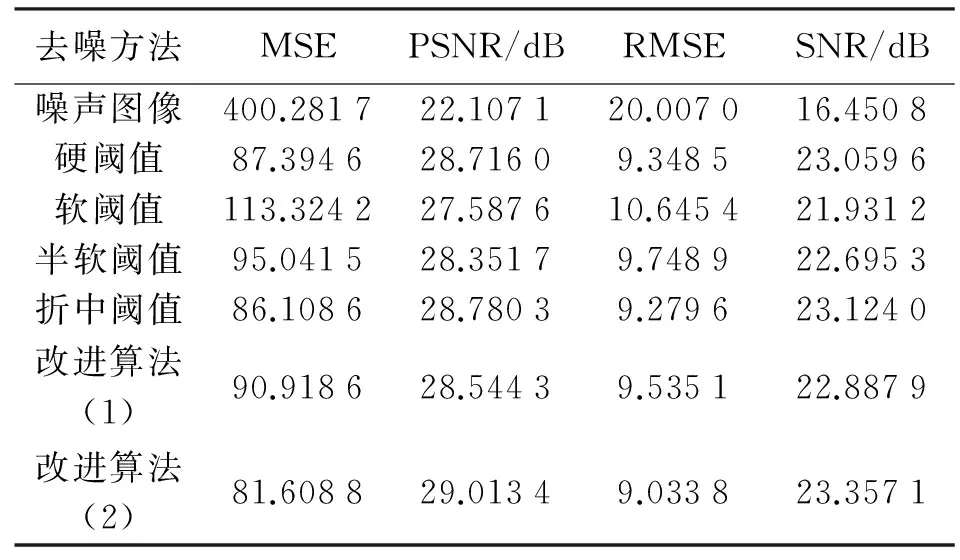
表1 各種閾值函數去噪的評價指標

圖1 閾值函數去噪處理結果

3.2.2 試驗2

在試驗1中通過閾值函數去噪方法對標準圖像Lena進行了比對試驗。在試驗2中運用去噪精度好的半軟閾值折中閾值，以及兩個新的閾值函數對遙感影像進行了去噪處理和精度評定[14-17]。如表1和圖2所示。

圖2 遙感圖像閾值函數去噪結果

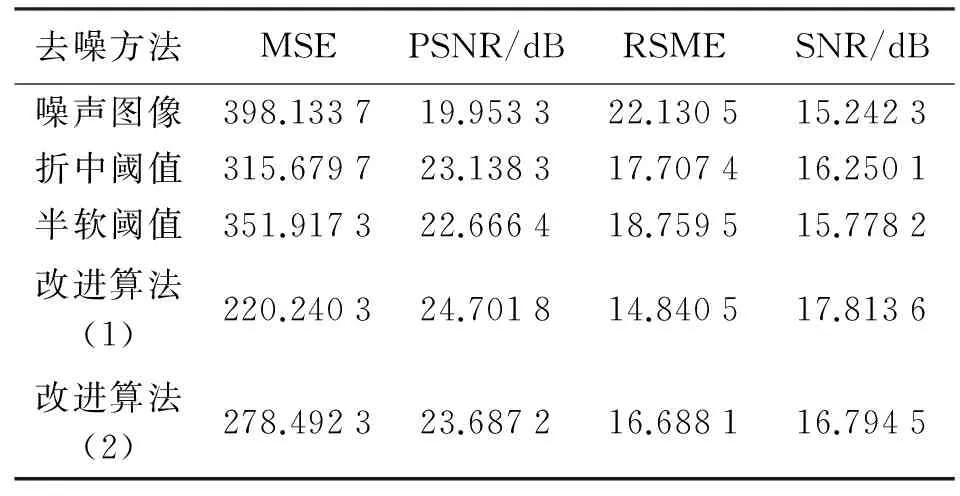
去噪方法MSEPSNR/dBRSMESNR/dB噪聲圖像398.133719.953322.130515.2423折中閾值315.679723.138317.707416.2501半軟閾值351.917322.666418.759515.7782改進算法(1)220.240324.701814.840517.8136改進算法(2)278.492323.687216.688116.7945

4 結 論

為了在傳統小波閾值去噪的基礎上進一步地改進閾值函數，本文通過添加調整系數和融合已有方法改進算法來達到去噪的效果，改進后的閾值函數的去噪試驗評價指標得到了更好的效果。通過對標準的檢測圖Lena和高分辨率遙感影像圖的去噪處理，由評價指標可以看出改進的兩個函數在去噪處理方面有所提高，但是所選擇的圖像不同，圖像的影響因素也不一樣，其復雜程度遙感圖像明顯要更高。通過試驗在相同的調整參數的情況下，為了使帶有噪聲污染的遙感圖像在后續的處理中更少受到噪聲的影響。改進算法(1)更加適合遙感圖像，其他的算法會造成遙感圖像光滑過度。對于復雜度比較小的檢測圖像，改進算法(2)比較適合。但是在處理的過程中，它們的評價指標明顯優于其他的方法。

參考文獻：

[1] 杜春梅,冀志剛,張琛. 基于小波閾值法的礦山遙感圖像非局部均值去噪[J]. 金屬礦山,2017(3):116-120.

[2] 張小燕,吐爾洪江·阿布都克力木. 小波變換的閾值圖像去噪算法改進[J]. 計算機技術與發展,2017(3):81-84.

[3] 崔金鴿,陳炳權,徐慶,等. 一種基于新型符號函數的小波閾值圖像去噪算法[J]. 電信科學,2017(1):45-52.

[4] 劉曉莉,任麗秋,李偉,等. 閾值優化的遙感影像小波去噪[J]. 遙感信息,2016(2):109-113.

[5] 李曉飛,邱曉暉. 基于小波變換的改進軟閾值圖像去噪算法[J]. 計算機技術與發展,2016(5):76-78.

[6] 謝家林,李根強,謝家麗,等. 改進閾值函數在圖像去噪中的應用[J]. 空軍工程大學學報(自然科學版),2016，17(1):72-76.

[7] 王琪,程彬,杜娟,等. 一種改進的小波閾值圖像去噪方法[J]. 計算機與現代化,2015(4):65-69.

[8] 白青,王軍鋒,王濤,等. 一種改進的小波閾值圖像去噪綜合模型[J]. 計算機技術與發展,2013(5):50-53.

[9] 楊立. 基于改進小波閾值函數的圖像去噪[J]. 重慶理工大學學報(自然科學),2013，27(2):93-95.

[10] 許麗群. 小波閾值去噪改進算法研究[J]. 電子測量技術,2010(8):43-45.

[11] 武文波,張迅,陳靜. 小波閾值的改進及在遙感圖像去噪中的應用[J]. 遙感技術與應用,2007(6):722-726.

[12] 馬先明,李永樹,謝嘉麗. 利用雙邊濾波法進行點云去噪的試驗與分析[J]. 測繪通報, 2017(2):87-89.

[13] 王忠美,楊曉梅,顧行發. 張量組稀疏表示的高光譜圖像去噪算法[J]. 測繪學報,2017,46(5):614-622.

[14] 唐鵬,郭寶平. 改進型閾值函數尋優法的小波去噪分析[J]. 信號處理,2017,33(1):102-110.

[15] 袁玉珠. 礦山遙感圖像小波域模糊隸屬度閾值去噪算法[J]. 金屬礦山,2017(4):123-126.

[16] 田江龍,屈衛東. 基于小波去噪的閾值函數改進方法分析[J]. 化工自動化及儀表,2017,44(3):243-247.

[17] 劉冰,劉雪梅. 基于改進小波閾值去噪的圖像增強算法[J]. 微型機與應用,2017,36(14):39-42.