風電塔筒屈曲承載能力提高方法研究

文 | 李劍波，李學旺，黃冬明

塔筒是風力發(fā)電機組重要的支撐部件，不僅承受著葉片、機艙、塔筒的重量，還承受著風輪旋轉產生的交變載荷以及風載荷，其強度決定了整機的安全性。鋼制塔筒的強度計算主要包括靜強度、疲勞以及屈曲，而塔筒的安全性通常由疲勞或屈曲決定；發(fā)生屈曲時，塔筒本身的最大應力沒有達到材料的屈服強度，即屈曲先于靜強度破壞而發(fā)生，因此屈曲承載能力計算對于塔筒強度計算來說非常重要。

塔筒的承載能力與經濟性是難以破解的一對矛盾，增大塔筒壁厚無疑可以提高塔筒的屈曲承載能力，但增大壁厚會導致塔筒重量急劇增加，經濟性較差。那么如何提高塔筒的屈曲承載能力而又經濟可行十分值得研究。本文將從理論和有限元分析兩個方面來研究風力發(fā)電機組塔筒屈曲承載能力的提高方法。

塔筒穩(wěn)定性理論分析

塔架結構屬于細長桿，可以從材料力學的角度用歐拉理論來分析其可以承受的最大臨界載荷。工程實際中，通常采用DIN標準對塔架屈曲承載的安全性進行計算。下面將分別從歐拉理論和DIN屈曲計算方法兩個方面來研究塔架屈曲承載能力提高方法。

一、歐拉臨界載荷

根據材料力學的知識可知，塔架可以簡化為一端固定一端自由的細長桿。其歐拉臨界壓力為：

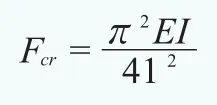
Fcr——歐拉臨界壓力、E——材料彈性模量、I——截面慣性矩、l——桿件長度

根據歐拉公式可知，塔架的屈曲承載能力與高度成反比，與彈性模量和截面慣性矩成正比。對于一款機組來說，其塔架高度l通常是固定的。而各種鋼材的彈性模量E大致相等，所以選擇優(yōu)質鋼材或者是低碳鋼并無很大差別。因此決定塔架屈曲穩(wěn)定性的主要因素是塔架的截面慣性矩I，而截面慣性矩由截面形狀決定。錐形鋼制塔筒的截面形狀為圓環(huán)，增大塔筒的直徑和壁厚都可以提高截面慣性矩，從而提高塔架屈曲承載能力，但是這一方法會明顯提升塔架的成本，降低經濟性。

二、DIN屈曲計算方法

DIN18800-4標準中給出了常量壁厚的柱形殼體的屈曲計算方法以及常量壁厚的錐形殼體的屈曲計算方法。實際中，塔筒為不同壁厚的鋼板焊接而成的錐形殼體。校核變壁厚的錐形塔筒需要把塔筒分為多個等壁厚的小段，把這些小段轉化為與所在塔段等長的長圓錐，再把長圓錐轉化為圓柱。 DIN18800-4屈曲計算標準中考慮了軸向應力、剪切應力和環(huán)箍應力三個分量對屈曲承載能力的綜合作用。其中軸向應力起決定作用，剪應力起次要作用，環(huán)箍應力的影響很小。為了簡化分析流程，本文主要考慮軸向應力分量對屈曲承載的影響。

軸向許用翹曲應力等于實際翹曲應力除以材料安全系數，按式（1）計算：

式中：σxSRd——軸向許用翹曲應力；σxSRk——軸向實際翹曲應力；γM——材料安全系數

實際翹曲應力等于特征屈服應力乘以縮減系數：

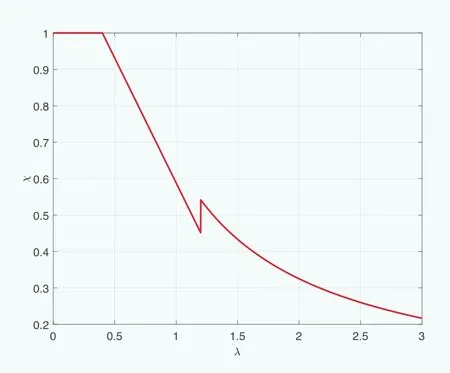
圖1 縮減系數與細長度的關系圖

式中： χ——縮減系數；fyk——特征屈服應力

而縮減系數又是細長度的函數，對于正常缺陷敏感度的外殼，其關系如圖1所示，橫軸為細長度，縱軸為縮減系數。

非量綱細長度λsx按式（3）計算：

式中：λsx——非量綱細長度；σxsi——軸向壓縮下圓柱的理想翹曲應力

軸向壓縮下圓柱的理想翹曲應力σxsi按式（4）計算：

式中：Cx——由長度決定的系數；t——塔筒壁厚；r——塔筒半徑

系數Cx根據外殼的長度確定。對于軸向屈曲，滿足下式時屬于長圓柱。塔筒一般分為四節(jié)，按照DIN標準，各個小節(jié)基本上都屬于長圓柱。

η根據支撐條件確定，取1或3（底段）。

由上述計算過程可知，提高材料強度在一定程度上可以提高屈曲承載極限，但是材料強度提高會導致縮減系數 χ減小，而縮減系數減小會使實際翹曲應力減小。為了定量分析材料強度對屈曲承載力的影響，取一節(jié)長15m，外徑4m，壁厚0.03m的等壁厚長圓柱塔筒進行計算對比。分別計算材料為Q345和Q390的兩種筒段的實際翹曲承載力。

由計算結果可知，提高材料強度對屈曲承載力影響較小，而且選用高強度的材料會導致焊接性能下降，進而影響塔筒焊縫的疲勞強度；另外高強度的材料對缺陷更加敏感，也會影響塔筒的屈曲承載能力。

塔筒穩(wěn)定性提高有限元分析

屈曲分析也叫穩(wěn)定性分析，就是求解結構從穩(wěn)定平衡過渡到不穩(wěn)定平衡的臨界載荷。采用有限元方法對結構進行屈曲分析時，一般有特征值屈曲分析和非線性屈曲分析兩種方法。特征值屈曲用于預測一個理想彈性結構的理論屈曲強度，這種方法計算簡便高效；非線性屈曲分析比特征值屈曲分析更加精確，但是有費時和計算量大等缺點。本文采用特征值屈曲分析方法研究加縱筋和橫向環(huán)筋對塔筒屈曲承載力的影響。取一節(jié)長15m，外徑4m，壁厚0.03m的塔筒，采用實體單元進行屈曲分析。分別研究加橫向環(huán)筋和縱筋對屈曲承載力的影響。

一、橫向環(huán)筋對屈曲承載力的影響

分別計算不加筋，加一個環(huán)筋，加兩個環(huán)筋的塔筒的屈曲承載能力。加一個環(huán)筋的模型中環(huán)筋加在塔筒中間部位，加兩個環(huán)筋的模型中每隔五米加一個，均勻分布；同理，加三個環(huán)筋和四個環(huán)筋均按均勻分布。加環(huán)筋的塔筒幾何模型如圖2－圖5所示。約束模型底部所有自由度，頂部加載彎矩Mx＝1e7kNm。

圖2 塔筒加一個橫向環(huán)筋的幾何模型

圖3 塔筒加兩個橫向環(huán)筋的幾何模型

圖4 塔筒加三個橫向環(huán)筋的幾何模型

圖5 塔筒加四個橫向環(huán)筋的幾何模型

表1 不同材料的實際翹曲承載力計算表

塔筒特征值屈曲分析的屈曲波形如圖6－圖10所示。

塔筒加環(huán)筋特征值屈曲分析計算得到的載荷因子如表2所示。從表中可知，加一個環(huán)筋時相對于不加筋載荷因子僅僅提高了0.38%，加兩個環(huán)筋時相對于不加筋載荷因子提高了0.95%，加三個環(huán)筋時相對于不加筋載荷因子提高了5.5%，加四個環(huán)筋時相對于不加筋提高了7.1%。由此可見，加一個或兩個環(huán)筋對塔筒屈曲承載能力的提高影響較小，而加三個或四個環(huán)筋對塔筒的屈曲承載有一定的提高；然而增加三個或者四個環(huán)筋時會導致塔筒重量急劇增加，更多的焊接也會帶來更大的焊接變形，制造精度難以保證。因此，通過增加環(huán)筋的方式來提高塔筒的屈曲承載能力不具可行性。

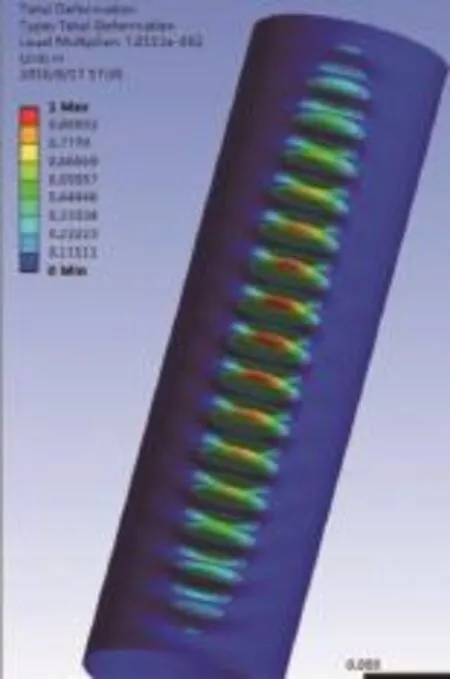
圖6 不加環(huán)筋時塔筒屈曲變形結果

圖7 加一個環(huán)筋時塔筒屈曲變形結果

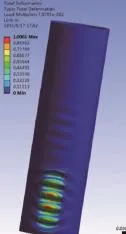
圖8 加兩個環(huán)筋時塔筒屈曲變形結果

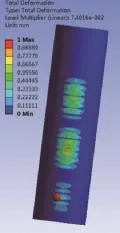
圖9 加三個環(huán)筋時塔筒屈曲變形結果

圖10 加四個環(huán)筋時塔筒屈曲變形結果

圖11 塔筒加一根縱筋幾何模型

圖12 塔筒加兩根縱筋幾何模型

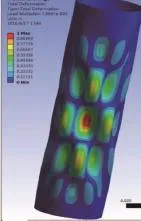
圖13 加一根縱筋（受壓）塔筒屈曲變形

圖14 加兩根筋塔筒屈曲變形圖

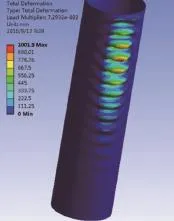
圖15 加一根縱筋且縱筋受拉塔筒屈曲變形圖

二、縱筋對屈曲承載力的影響

為了研究加縱筋對塔筒屈曲承載能力的影響，分別計算塔筒加一根縱筋和兩根縱筋的屈曲承載能力，同時研究加載方向對屈曲承載的影響。加筋的幾何模型如圖11－圖12所示。塔筒加縱筋載荷因子計算結果如表3所示。屈曲變形結果如圖13－圖15所示。從表3載荷因子計算結果可知，塔筒加一根縱筋且使縱筋受壓時塔筒屈曲承載能力提高了14%，加一根縱筋且使縱筋受拉時屈曲承載能力提高了4%，加兩根縱筋時屈曲承載提高了17.67%。由此可見，加兩根縱筋時對于提高塔筒的屈曲承載能力十分有效，而若再增加縱筋數量，一方面會導致塔筒重量的增加，降低經濟性；另一方面再增加縱筋需要更多的焊接工裝，同時會造成更大的焊接變形，難以保證塔筒的制造精度。

表2 塔筒加環(huán)筋載荷因子計算結果

表3 塔筒加縱筋載荷因子計算結果

攝影：車傳江

結論

本文從理論分析和有限元仿真兩個方面對提高塔筒屈曲承載能力的方法進行了研究。歐拉理論分析表明，提高塔筒截面慣性矩可以有效提高塔筒的屈曲承載能力；DIN屈曲計算方法研究表明，鋼材的強度對塔筒屈曲承載能力影響較小；有限元分析結果表明，加一個或兩個環(huán)筋對塔筒屈曲承載能力的提高影響較小，加三個或四個環(huán)筋對塔筒的屈曲承載有一定的提高，然而增加三個或者四個環(huán)筋時會導致塔筒重量急劇增加，更多的焊接也會帶來更大的焊接變形，制造精度難以保證。因此，通過增加環(huán)筋的方式來提高塔筒的屈曲承載能力不具可行性；而加兩根縱筋就可以明顯地提高塔筒的屈曲承載能力，具有實際可行性。本文研究結果對于經濟可行地提高塔筒的屈曲承載能力提供了參考。