燃氣渦輪發動機渦輪葉片熱障涂層排產優化問題研究

謝 錚，鮑曼雨，何 箐

（中國農業機械化科學研究院， 北京 100083）

引言

面向訂單的生產模式（Make toorder，MTO）是根據客戶發來的訂單信息中所規定的交付期限以及交付數量進行生產排產，必須配合訂單的進廠時間和生產所需資源的準備時間，確定產品每一道工序的開始時間和完成時間，保證各生產環節的協調進行。OEM生產模式是社會化大生產、大協作趨勢下的一種資源合理化有效利用的模式之一，諸如成本、供貨周期等因素，OEM企業面臨極大的交付壓力[1]。在此背景下，MTO生產方式被諸多制造業企業所使用，尤其是設計特種工藝、特殊機械產品的制造加工業。

航空發動機是飛機的“心臟”，是現代工業“皇冠上的明珠”，可以代表人類工程技術的最高智慧；航空發動機的高壓渦輪熱端部件是其制造的難點和關鍵之一，也是服役工況最為惡劣的部件，其中渦輪葉片尤為關鍵[2]。葉片熱障涂層技術由于能有效提高基體的服役溫度和使用壽命，提高有效的高溫氧化腐蝕防護效果，因而被稱為現代航空發動機渦輪葉片制造的三大關鍵技術之一，是現代高性能航空發動機不可或缺的關鍵技術。葉片熱障涂層的生產具有典型的特種加工和短流程性材料特征，雖然工序繁瑣程度有限，但涉及兩個核心：關鍵工藝能力和過程控制制約涂層產能和質量；檢驗工序為復雜、耗時的逐個檢驗。同時基于上游渦輪葉片生產模式，從投料、鑄造、機加、打孔、釬焊等復雜工序流程，渦輪葉片的產出為典型的非均衡生產模式。基于上述渦輪葉片熱障涂層來料特點以及涂層生產特性，通過合理的資源配置，提高渦輪葉片生產流程中熱障涂層工序生產效率，是保障經濟性和交付周期的關鍵[3]。

1 等離子噴涂葉片熱障涂層生產模式分析

本文研究對象為等離子噴涂葉片熱障涂層，在自動化噴涂技術狀態未貫徹前，存在一個階段的人工噴涂和自動化機械手噴涂工藝狀態并存期，由于兩種工藝狀態加工周期等方面存在不同差異，導致排產的難度和生產效率提升的復雜程度顯著提高，因為該階段生產模式和數據情況作為本文的研究對象。

該生產過程中涉及編號為A、B和C的三類葉片零件的生產，其噴涂工藝和要求也不一致。等離子噴涂葉片熱障涂層典型生產工序如圖1所示。

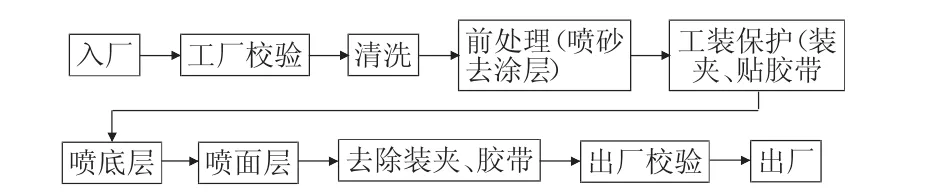
圖1 等離子噴涂葉片熱障涂層生產工序

葉片涂層的生產特點是部件本身交付節點有嚴格限制，葉片部件工序較長，而葉片涂層為其最后幾個工序之一，因而后期工序生產時間往往容易集中在臨近交付期或出現壓縮周期的快速交付的情況，所有OEM涂層訂單必須接受并按期交付，延期交付僅個別和特殊情況下可接受；因而產能平衡和排產過程中，盡量避免出現延期交付，依據緊急程度，進行排產，減少超期訂單的發生；如出現超期預期，評估現有訂單的優先級，減少系統性風險發生。基于上述具體生產模式和原則，對目前葉片涂層產品生產過程系統分析如表1所示。

針對表1中生產工序和不同零件各工序工作時間，同時為了避免產能擴張是過多的設備投入導致浪費，設計了一種針對有限產能資源配置生產環節下基于啟發式算法的產能規劃方法。同時由于來貨訂單時間的不規律性，通過啟發式算法規劃產能的分配，確定訂單生產的開始時間，采取適當的調整訂單順序，來應對瓶頸工序的產能短缺。

2 符號和假設

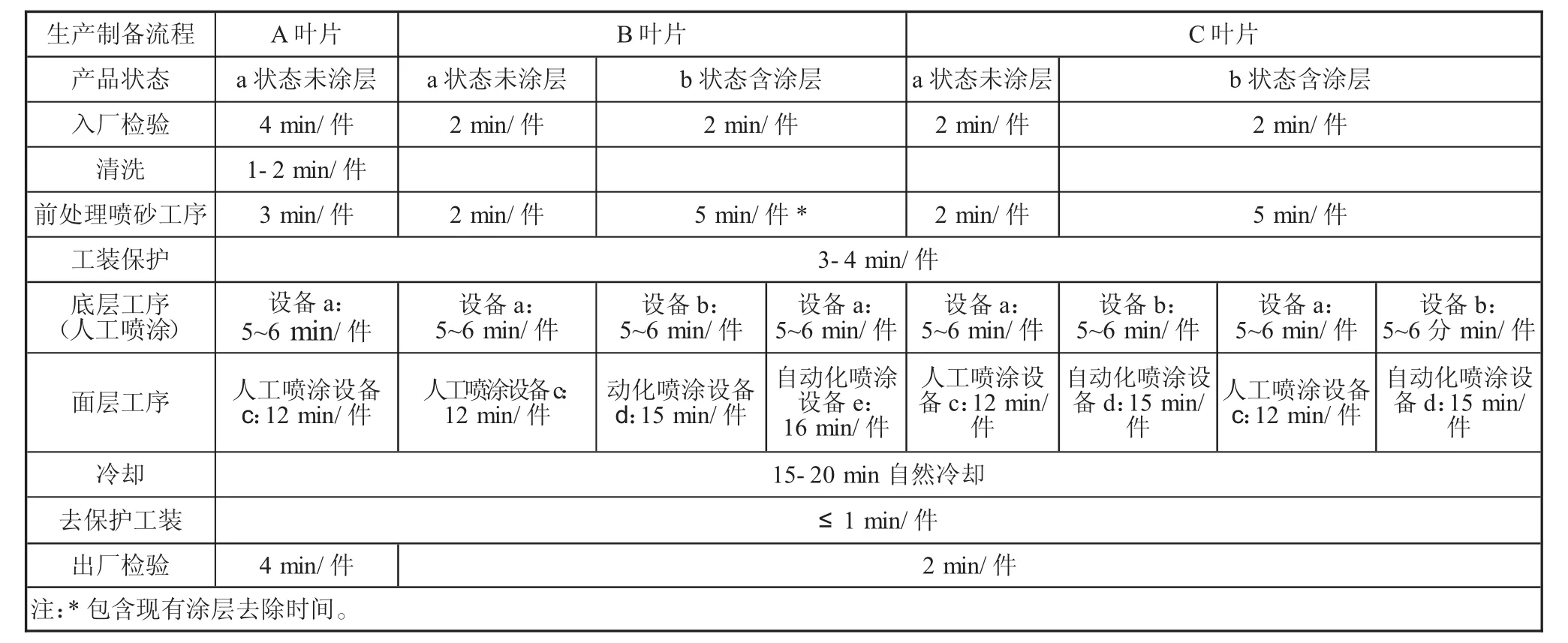
表1 產品特點及工藝流程

本文中所使用的主要符號如下：

s為工序，s=1，2……，s；P 為產品，P=1，2，……，P；O 為訂單，O=1，2，……，O；t為時間，t=1，2，……；TNOW為當前時間；RWO為所需工作量；Op為產品p所需總工序數；TAR為調整投產時間；Rco為臨界比率；TcP（s1，s2）為工序s1與 s2之間的生產周期；DD為交貨日期、到期日；LE為設備 E 的負載；TOR（o）為訂單 o 剩余的處理時間；TLR為最晚投產時間；Tpp（s）為產品p在工序s的加工時間；Tpsp為計劃生產時間；TRCp為產品p在工序s中剩余的生產時間；Tslack（o）為訂單o的松弛時間；TLE為設備E工作的總時間。

本文負載模型的主要假設如下。

一是假設設備每天的工作量是8 h以分鐘記為480分；二是A產品為23件一批，B產品15件為一批次，C產品21件為一批次。訂單一般以批次為單位，成倍數計數；三是對于所有不確定生產時間的工序按較大的加工時間進行處理，在避免隨機條件影響的同時，更貼近實際生產；四是將噴砂這一工序的產能上限設定為4臺設備所能提供產能的100%，以使投產批量對投產時間產生影響；

五是模擬計算過程中，產品到達下一工序時不需等待，可以直接進行下一工序加工。

3 有限產能模型

3.1 模型設計

本文的仿真過程中，對有限產能模型和各模塊、邊界限定條件進行了規劃，有限產能代表每臺設備時間負載上限，每臺設備的負載上限不應超過該設備負載的100%。當達到負載上限時，多余的工作量將轉移至并列設備或排隊等候。在訂單的優先級被確定后，開始按訂單進行生產，同時進行設備工作的負載積累步驟。有限產能規劃包括順序選擇和優先級設置模塊、投產模塊、負載積累模塊、工作負載平衡模塊，有限產能設計模型[4]，如下頁圖2所示。

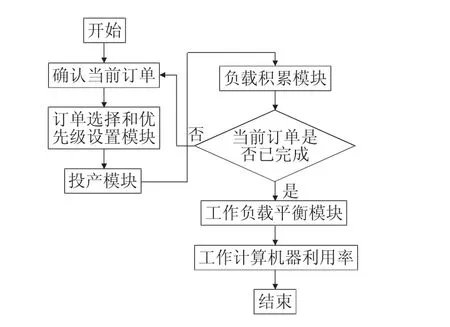
圖2 有限產能設計模型

利用投產模塊確定訂單交貨時間點和設備產能。選擇訂單投產時間的目的在于在不超期的情況下，盡可能保證每一階段內的設備負荷平衡，防止產能過剩或產能不足。工作負載積累模塊根據處理步驟和步驟周期時間計算剩余過程的開始時間，以便為未來的工作量供參考[5]。

3.2 模型建立

生產周期包含生產加工、等待、運送時間，而產品p則是在工序S中流轉，工序的生產周期作為產能規劃的重要參數，決定在制品的到達時間和離開時間。因此，所需的產能可以通過適當的時間積累進行確定，同理可以通過設備工作時間確定設備本身的利用率，生產周期的表達見式（1）。

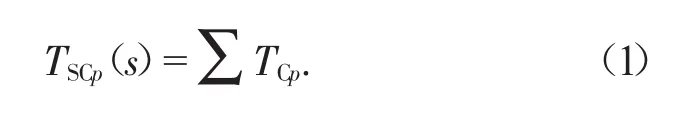
3.2.1 訂單模塊

訂單投產模塊算法的實施步驟如下：通過當前物料情況確定新訂單投產時間；其次，確定之后每一工序的開始時間，同時確定每一工序可以并行生產的設備數量，并通過負載積累模塊進行負載累計；上述步驟完成后，以最小負載所對應的投產時間作為ART協助確定更優的投產時間。

步驟一：計算訂單A的最晚投產時間（TLR），公式（2）中設定t為最晚投產時間。

步驟二：s=1。

步驟三：如果s≤op，則前往步驟四，否則，前往步驟五。

步驟四：計算每一工序的開始時間。如果s∈有并行設備的工序：

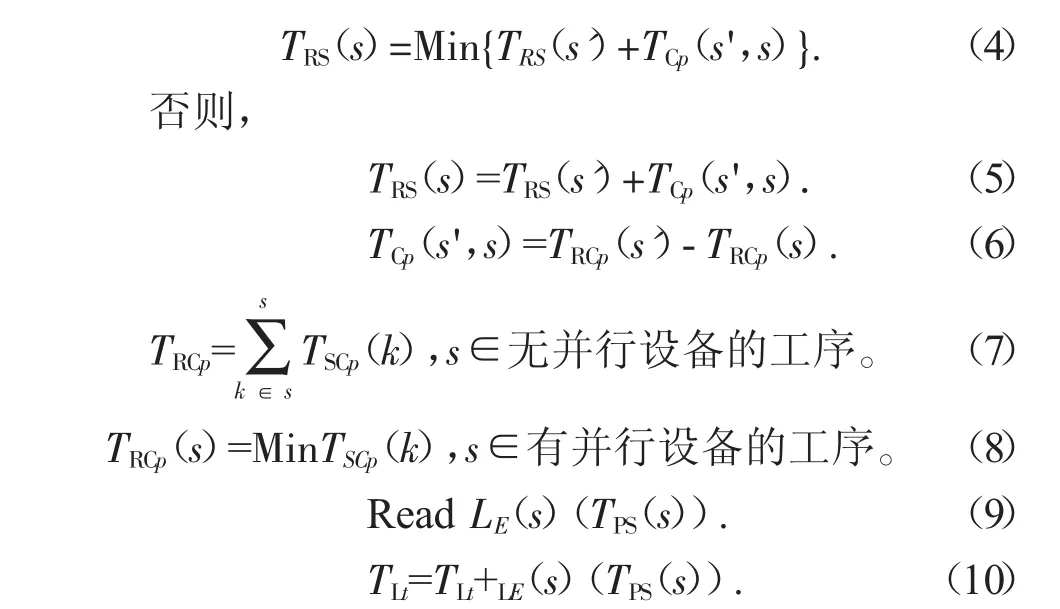
其中：s=s+1，返回步驟三。

步驟五：如果 t＞1，t←t-1，返回步驟二，否則，前往步驟六。

步驟六：

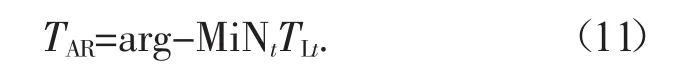
返回系統。

3.2.2 負載模塊

在負載積累模塊中，可以根據工序生產周期計算剩余步驟的計劃開始時間，作為并行設備負載積累的參考。如果當前進行的是并行工序，其PST可以由式（10）得出：

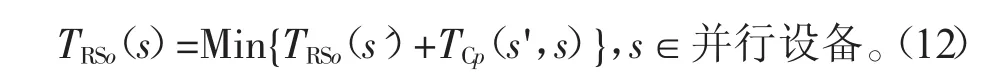
步驟為：計算處理步驟的開始時間如式（11）。把工序順序所需設備確定，確定后得到的結果，將用負載來選擇，并重新計算，得到下一道工序順序所的所需設備。當所有的處理工序都完成時，設備的負載積累完成。

負載積累模塊的算法說明如下：

第一步，計算選定步驟的TPS（s）;

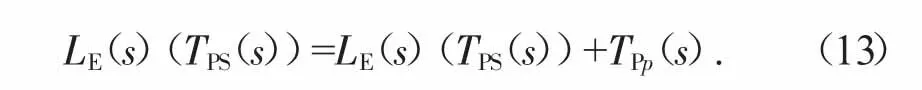
第二步，當設備完成生產加工后，計算每臺設備的負載積累，將結果用來計算得到設備的利用率百分比；

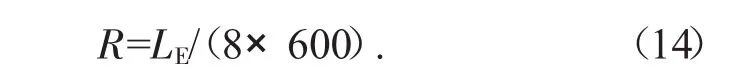
步驟三，確定是否所有工序均已完成。如果有任何一個工序沒有完成，進行第一步。否則，返回無限產能規劃系統（CPS）。如果 s＜op，s=s+1，進行第一步。則返回系統。

3.2.3 訂單選擇和優先級模塊

每批訂單都應根據訂單的優先級順序來設置模塊。該模塊的預期目標是盡可能保證準時交貨，用以區分同批次產品加工順序，獲得最高生產效率。與此同時還可以通過調整優先級，滿足客戶在生產緊張時對訂單的加急要求。

本文中基于訂單分析模塊計算出的每個訂單的松弛時間，設置訂單的優先級。通過計算當前日期和計劃到期日的時間差并減去剩余處理時間來設置訂單的優先次序，滿足訂單的到期日。松弛時間越小，越接近到期日的訂單將被賦予更高的優先級。

訂單選擇和優先級的算法設置模塊如下：

步驟一o=1。

步驟二：計算剩余的生產時間，TRC（o）。

步驟三：計算訂單o的松弛時間

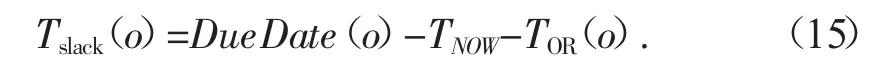
步驟四：如果 o＜0，o←o+1 返回步驟二，否則，去往步驟五。

步驟五：基于松弛時間，設置訂單優先級，并返回有限產能規劃系統。

3.2.4 工作負載平衡模塊

在工作負載平衡模塊中，必須考慮產能約束，如果一臺設備的容量要求超過其容量的100%，則訂單的投產時間需要進行調整，則可能導致訂單過期。

步驟一：通過負載積累模塊反映的負載情況確定負載超出最大產能的日期ti并依次排列，以及負載小于最大產能的日期tj，依照次序排列。

步驟二：LEi-1＞1-LEj，前往步驟三，否則，前往步驟四。

步驟三：LEi=LEi下一順位，返回步驟二。

步驟四：將ti的多余工作量轉移至tj。

按照以上步驟，可以進行負載轉移，降低機器平均負載，提高企業機器利用率。

4 計算結果

訂單需求如表2所示，訂單編號表示了訂單到來順序，各訂單含各型號產品的批次數量及產品狀態。

表3是按照訂單到來順序進行排產的有限產能計算結果，各工序的工作時長包含了工件在生產過程中的等待時間。從表中可以看出面層DLZ設備工序的工作時長最大，是整個生產流程的瓶頸工序，其產能將影響整個加工系統的工作速度。松弛時間為負，代表著企業難以在交貨期到來之前完成產品生產。按順序加工的排產方法會導致大量的等待時間，造成產能浪費，增加成本，且無法按期交付。

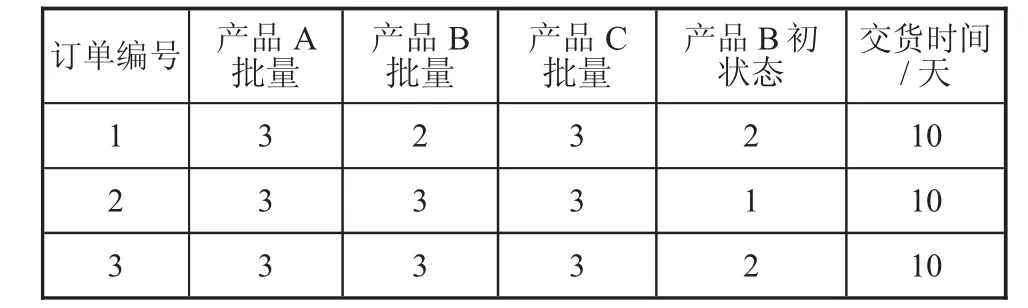
表2 訂單需求

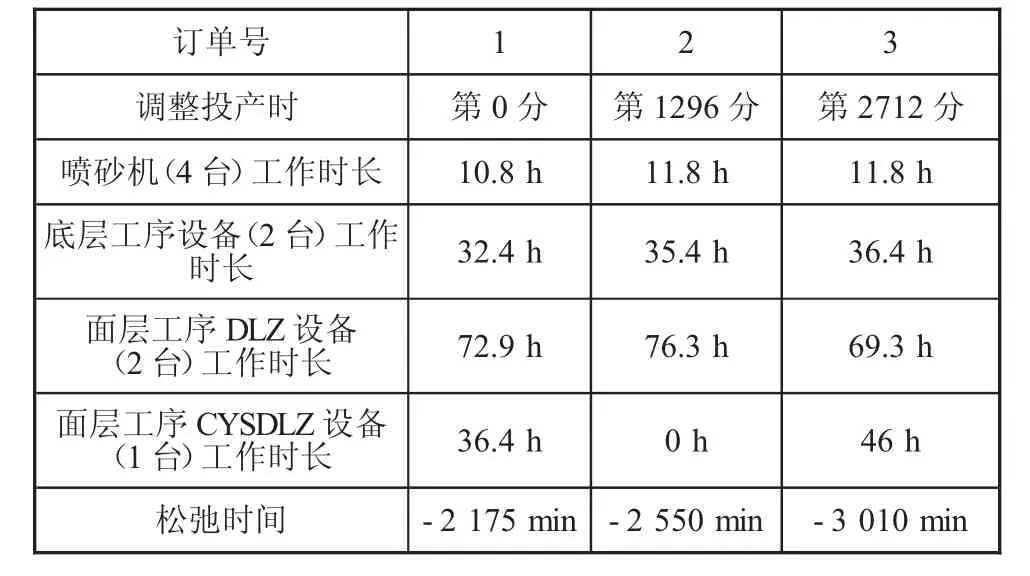
表3 按照訂單順序進行排產的仿真結果

調整排產順序后的結果如表4所示，如果設備當前生產速度保持不變，三個訂單均可按時交貨。依照松弛時間的多少來確定到來訂單的投產順序，3份訂單中，應當首先投產的是訂單3，其次是訂單1，訂單2則可以最后生產。

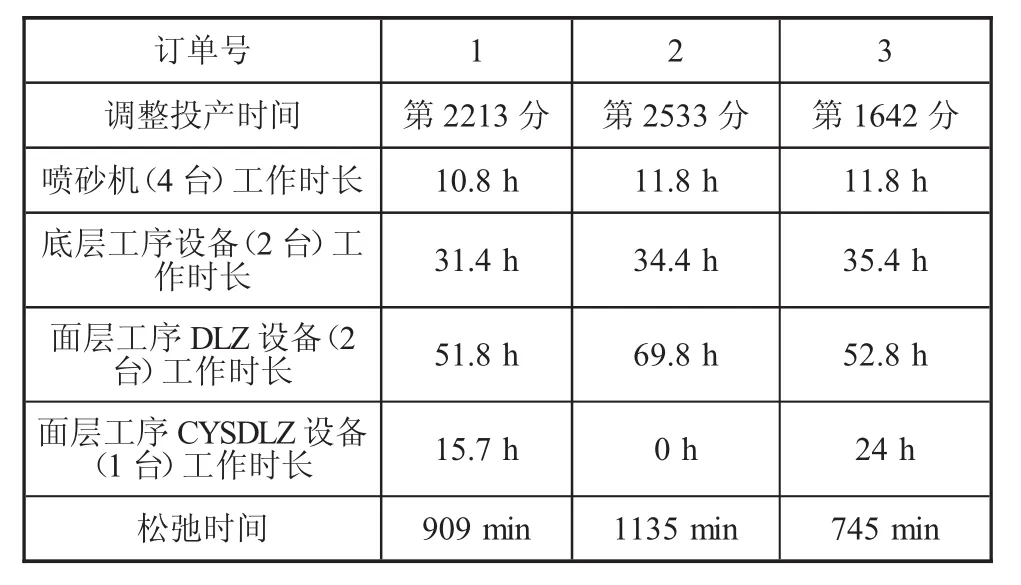
表4 調整排產順序后的仿真結果

5 結論

從以上結果可以看出，企業可以考慮增添底層及面層DLZ設備，而噴砂工序由于設備較多加工較快，可以考慮減少設備數量或安排更多生產任務提前排產。本文提出的優化算法是有效的，能夠通過排產縮短工序之間的等待時間，進而縮短整體加工時間，提高企業準時交貨的能力。

[1]倪衛濤，周晶.MTO生產模式的交貨期決策模型及其分析[J].工業工程，2008，11（2）：54-55.

[2]陳光.航空發動機結構設計分析[M].北京：北京航空航天大學出版社，2006.

[3]鐘穎虹.燃氣輪機透平葉片熱障涂層的研究[D].北京：機械科學研究總院，2015.

[4]Arthur V.Hill.,Julie M.Heys,Eitan Naveh,A model for optimal delivery time guarantees[J].Journal of service Research.2000,21（3）：254-260.

[5]Soman W.Goward GWU.Progress in coatings for gas turbine airfoils J.Surf.Coat.Tech.1998/08/09:7 379.