數學教學應重視由特殊到一般的建構學習

江西師大數學與信息科學學院 (330027)

付奕玲*

1 引言

一般地，人們對特殊事物往往易于接受、理解，由特殊到一般是人們普遍的認識過程.同樣的，學生數學學習過程也往往是在特殊條件下進行分析，然后再推廣應用于相同屬性的對象.這種從個別或特殊的事物所做的判斷，再推廣到同類事物的判斷，即為從特殊到一般的推理.數學概念是建立在相關法則、公式及定理基礎上的，所以要理解一個數學概念，就必須圍繞這個概念逐步構建相應的概念網絡，使概念之間形成網絡節點，網絡的結點越多、路徑越豐富，概念理解相對就越深刻.數學定理是數學知識中的重要基礎和工具，定理的證明和發現過程對培養學生的創新能力和邏輯思維具有不可替代的重要意義.數學學習中往往需要將把認知結構中已有特殊的概念和定理，與一般的概念和定理建立起合乎學生理解的邏輯關系，并努力形成實質性的聯系，從而達到有意義的數學建構學習的目標.

2 案例

案例1 由函數關于原點對稱推廣到關于任意點對稱

“數學科學特別展示了秩序、對稱和極限，這些是美的最偉大的形式”.對稱，是數學美的一種表現形式，這種對稱美在函數知識內容里有充分的詮釋.比如奇函數的定義為：對于函數f(x)的定義域D內任意一個x，如果都有f(-x)=-f(x)，則稱f(x)為奇函數.由定義可知奇函數圖像關于原點對稱.原點是一個特殊點，其本質特征是關于點的對稱關系，如果將定義的特殊屬性推廣到一般條件下，最簡單的就是關于任意點(a,b)的對稱問題.

奇函數關于原點對稱，從函數圖像觀察可知，就是函數中對應點的橫坐標關于y軸對稱，縱坐標關于x軸對稱，驗證關系式亦成立，由此猜想是否關于任意點(a,b)的對稱也就是函數上的對應點橫坐標關于x=a對稱，縱坐標關于y=b對稱.根據對稱的性質，自變量關于x=a對稱，設其中一點的橫坐標為x,則另一個對稱點的橫坐標為-x+2a；對應點的因變量分別為f(x),f(-x+2a)，其中一個自變量縱坐標為f(x)，那么另一個關于y=b對稱的對應點的自變量縱坐標的值應該是-f(-x+2a)+2b，即f(x)=-f(-x+2a)+2b，也可以變換為f(a+x)-b=-f(a-x)+b.這是分析和猜想的結果，要確定是否為此關系式，還需要經過驗證.

一般又可開展以下的特殊化驗證過程：(1)奇函數關于原點對稱，把a=0，b=0代入f(x)=

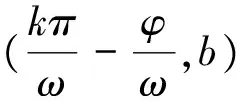
案例2 由勾股定理推廣到余弦定理

勾股定理是數學內容中的“千年第一定理”，表示的是直角三角形斜邊的平方等于兩直角邊的平方和，即c2=a2+b2.定理表示的是三角形邊與邊之間的關系，其中有一個特殊條件就是直角三角形，所以應該是邊角之間的關系，自然地會猜想一般的三角形是否也存在類似的邊角關系.因為特殊三角形的邊角關系滿足一般三角形的邊角關系，所以一般三角形的邊角關系式中不可能是在c2=a2+b2中的一項或幾項中乘以某個數或式子，故一般三角形的邊角關系式應該是在c2=a2+b2的基礎上存在另外的項.

猜想以其中一個角為30°的特殊直角三角形為例進行探索，如圖1所示，∠C=90°，∠A=30°，c=2.

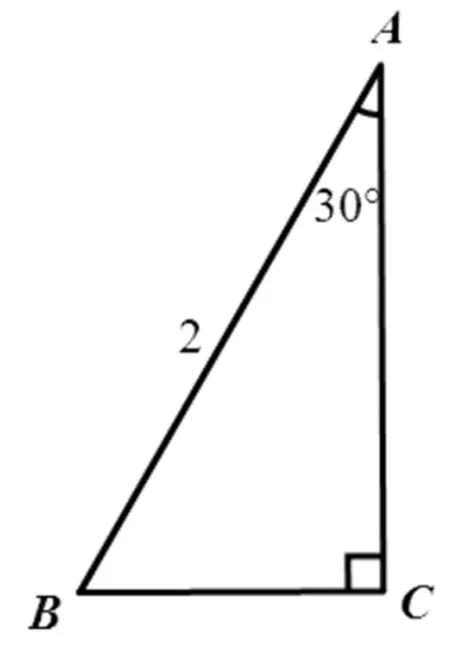
圖1

猜想1c2=a2+b2+x(x表示未知項)，當∠C=90°時，最后一項不存在，所以在未知項里面可能有cosC，即被求邊的對應角的余弦值.

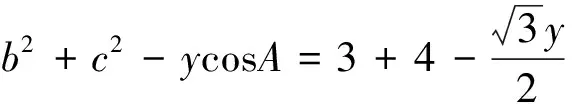
c=2.

猜想7a2=b2+c2-c2bcosA，推理可知，在一般式中，b，c的地位應該是一致的，所以添加的一項中應該也只有一個c，所以z=2c更合理.

猜想8a2=b2+c2-2bccosA，如果猜想正確，即b2=a2+c2-2accosB也成立，將已知的邊角的值代入最終猜想的一般式中，驗算得出式子兩邊的值相等.

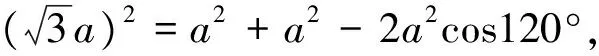
3.結語

由特殊到一般是數學建構學習的一種重要方式，這種學習方式要求教師在數學教學過程中應重視數學內容的特殊內涵分析、提煉，并作廣泛遷移.教師不應該是把現成的結論教給學生，而是根據數學內容的發生發展過程，創設問題情境，充分利用各種方式方法，設計系列問題，增加輔助環節，并讓學生通過大量的圖形觀察和實際問題的演算，使直觀想象到發現猜想和歸納，最后進行結論的驗證和理論證明，從而使學生親歷數學知識的建構過程，逐步掌握數學內容的本質方式和方法，提高學生學習興趣和學習效率，真正發揮由特殊到一般的數學建構學習過程在數學教育中的育人價值.