撥開云霧見月明
——源于一節隨聽課對一道數列題的講授而引發的探究

廣東省云浮市新興縣新興理工學校 (527400)

陳偉彬

偶爾隨聽了一節年輕老師的“推門”課.下面原汁原味地再現該年輕老師的“完美解法、優秀解法”.

生：起立！老師好！

師：同學們好，請坐下！這節課我們先講解一下兩天前中段考題中的一道數列題(板書).

題目在等差數列{an}中，當且僅當n=6時，Sn取得最大值，則使Sn>0的n的最大值是 .

師：從評卷得分的情況來看，全班52人得分率很不理想：有40人的答案完全錯誤；有7人的答案只寫對部分，如只寫n=11(或只寫n=12)；有5人不作答.

師：這道題目若借助于拋物線的圖像來求解是很直觀、很完美的.下面展示該完美解法：

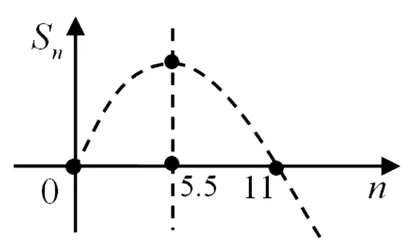
圖1

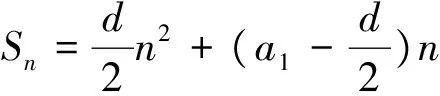
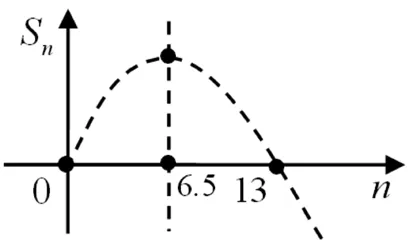
圖2

②當對稱軸n=6.5時，如圖2，由對稱性知，S13=S0=0，當對稱軸向左微移時，顯然有S12>0且S13<0.綜合以上①②得，要使Sn>0的n的最大值是11或12.

師：下面再講解中段考中的概率題目(以下的講課內容本文略)

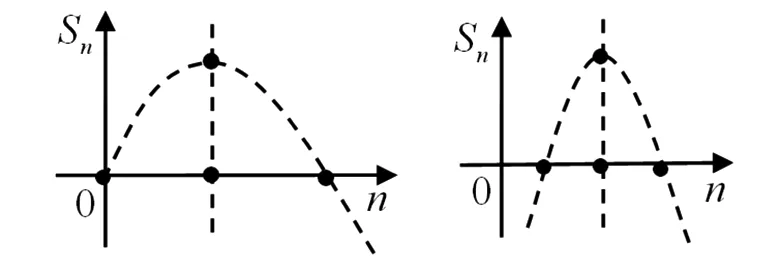
圖3 圖4

點評：該法是借助于二次函數的圖像，并且取兩個極端對稱軸位置，再依拋物線的對稱軸向右向左微移時，慢慢觀察圖像的變化，從而體會出(注：對學生來說有困難)S11>0且S12<0，或者S12>0且S13<0，從而得出結論.課后通過原年輕老師對全班學生的問卷調查，發現學生對老師的“完美解法、優秀解法”并不是很領情，學生普遍感到吃力、難以接受，即對二次函數Sn的圖像，老師沒有作相應的知識鋪墊就一下畫出過原點的圖3情形，那老師是怎樣想到的？若首項a1<0，則S1=a1<0，此時圖像很可能是不過原點的圖4情形，若是圖4情形，那如何判斷S11、S12、S13的正與負呢？總之，老師的解法很直觀、很正確、很完美，但心中很糾結，總感覺有問題如哽在咽.

在中段考后的教研活動中，詢問了幾個同事，都基本上類同上面“完美解法”的思路.當問到除此之外有沒有更為學生所接受的通俗易懂的解法時，同事們都說沒想過.對該“完美解法”，本文作者不想做過多的評價，但遺憾的是：在“完美解法、優秀解法”的背后還隱含著一些深層問題沒有跟學生一起探討.這些深層問題知識的缺失，可能會影響相類似題目的通性通法解決，而上面“完美解法、優秀解法”只是一個解法的個案.下面就這個“深層問題”作進一步的囊中探物，從難到易的探究，以便達到“撥開云霧見月明”找到更佳的通性通法，以饗讀者，引起廣大師生共鳴.

探究之一：結合二次函數Sn的圖像，探究對稱軸在三個特殊位置并相應的向左右平移，全面感知Sn的正負變化，從而得出結論(本質上是仿年輕老師的“完美解法、優秀解法”，但更完整).

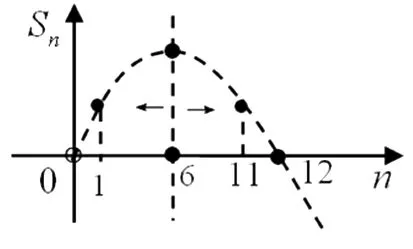
圖5

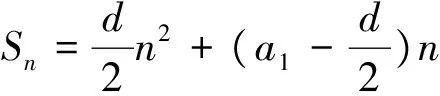
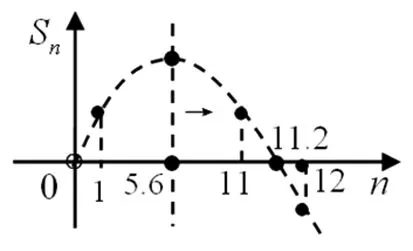
圖6

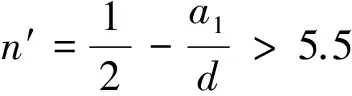
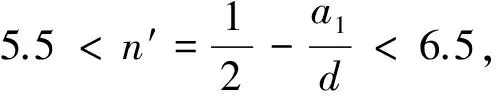
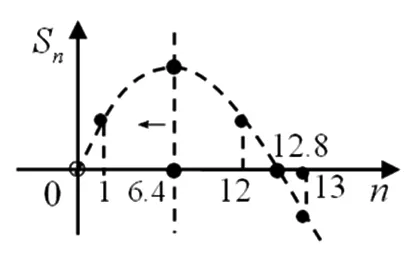
圖7

點是n=0和n=12.8，所以S0=0和S12.8=0，又Sn在區間(6.4,+)上單調遞減，所以S12>S12.8=0且S130的n的最大值是12.

綜合①②③可知，使Sn>0的n的最大值是11或12.

評：此法較繁瑣，適合培養運算的基本功與慎密的思維品質，以及空間想象能力.

探究之二：以對稱軸為切入點進行分類討論，討論軸的位置，判斷Sn的正與負變化.

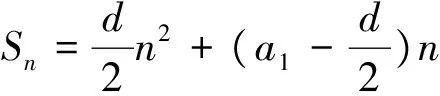
①當對稱軸5.50且S12≤0，此時使Sn>0的n的最大值是11;

②當對稱軸60且S13<0，此時使Sn>0的n的最大值是12.

綜合①②知，使Sn>0的n的最大值是11或12.

評：此法較“探究之一”簡潔，但思維能力與邏輯推理能力要求較高，不易達到最終目標.

探究之三：函數法——以對稱軸為切入點，通過構造數列“和”函數，并研究“和”函數的性質，構造不等式來確定n的取值范圍.

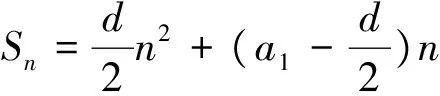
評：此法思維量不大，計算量少，易于操作，適合廣大學生，是解此類題的主流.

探究之四：依據題意先確定數列的正負分界項an>0且an+1≤0(或an≥0且an+1<0)，并借助于等差數列的性質ap+aq=am+an來等價轉換，從而導出Sn>0且Sn+1≤0(或Sn≥0且Sn+1<0).

分析：當且僅當n=6時，S6取得最大值，則公差d<0，同時a1>0，a2>0，a3>0，a4>0，a5>0，a6>0且a7<0.

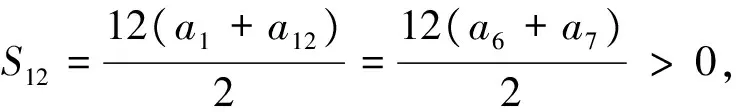
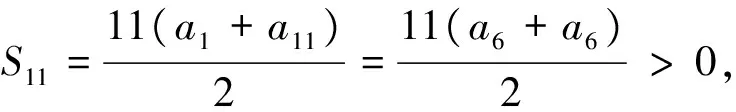
綜合①②知，使Sn>0的n的最大值是11或12.

評：此法簡潔、明快，但要儲備基礎知識，如ai>0(i=1,2,3,4,5,6)且a7<0，以及靈活應用等差數列的性質等價轉換.否則難以入手.

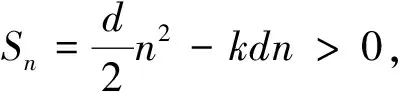
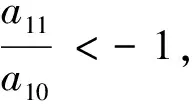
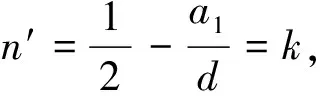
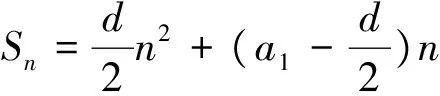
例2 設等差數列{an}的前n項和為Sn，已知a3=12，且S12>0，S13<0，①求公差d的范圍；②問該數列前幾項和最大？請說明理由.

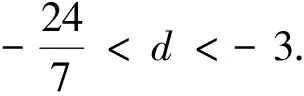
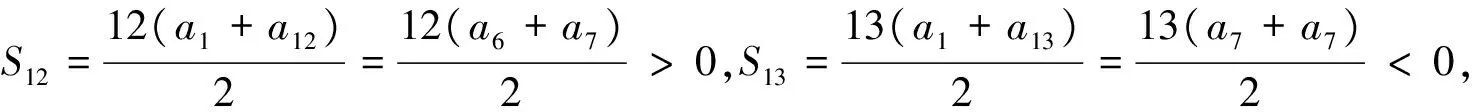
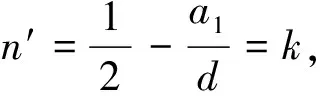
下面補充4道原創題目，供嘗試：

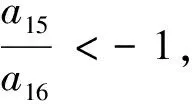
(答案為n=31)

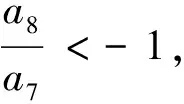
(答案為n=13)

3.在等差數列{an}中，當且僅當n=13時，Sn有最大值，則使Sn<0的最小n值為 .

(答案為n=26或27)

4.等差數列{an}中，當且僅當n=10時，Sn有最小值，則使Sn<0的最大n值為 .

(答案為n=19或20)

探究后的體會：解決諸如“當n為何值時，使Sn的值最大(小)”或“使Sn>0(Sn<0)的n的最大(小)值是多少？”的數列題目的通性解法的獲得，是緣于對“完美解法”的不知足而誘發一系列的由難到易，去粗存精，剝絲抽繭，整合優化等“撥開云霧見月明”的深入研究的結果.本文經探究所獲得的兩種通性通法，即“探究之三”與“探究之四”，若能為你處理該類數列題帶來一些新意的話，那作者的寫作目的也就達到了.