以阿波羅尼斯圓為背景的試題探究

浙江省衢州第二中學(xué) (324000)

劉瑞富

在近十年的高考中，以阿波羅尼斯圓為背景的考題不斷出現(xiàn)，備受命題者的青睞，本文通過(guò)列舉近幾年的高考及競(jìng)賽試題，講解與阿波羅尼斯圓有關(guān)的一些結(jié)論，進(jìn)一步加強(qiáng)對(duì)與此圓與關(guān)的試題的認(rèn)識(shí).

問(wèn)題的起源：

(1)人教A版必修2課本第124頁(yè)B組第3題.

(2)人教A版必修2課本第144頁(yè)B組第2題.

已知點(diǎn)M(x,y)與兩個(gè)定點(diǎn)M1,M2距離比是一個(gè)正數(shù)m，求點(diǎn)M的軌跡方程，并說(shuō)明軌跡是什么圖形(考慮m=1或m≠1兩種情形).

將此問(wèn)題一般化，我們有：

圖1

可以看出：(1)圓心與兩定點(diǎn)A,B在同一直線(xiàn)上；(2)是以分線(xiàn)段AB所成的比為λ的內(nèi)外兩個(gè)分點(diǎn)為直徑的圓.

例1 (2013江蘇高考題)如圖2，在平面直角坐標(biāo)系xOy中，點(diǎn)A(0,3)，直線(xiàn)l:y=2x-4．設(shè)圓C的半徑為1，圓心在l上．(1)略;(2)若圓C上存在點(diǎn)M，使MA=2MO，求圓心C的橫坐標(biāo)a的取值范圍．

圖2

解：(1)設(shè)點(diǎn)M(x,y),由MA=2MO，知

點(diǎn)評(píng)：本題解決的難點(diǎn)在于探求動(dòng)點(diǎn)M的軌跡方程，而點(diǎn)M的軌跡就是著名的阿波羅尼斯圓，得出點(diǎn)M的軌跡為圓后，問(wèn)題即轉(zhuǎn)化為兩個(gè)圓的位置關(guān)系.

圖3

命題1 如圖3，已知圓O的直徑為MN，在直線(xiàn)MN上有兩點(diǎn)A,B，若滿(mǎn)足

?(OA-OM)·(OB+OM)=(OA+OM)·(OM-OB)?OA·OB=OM2=r2.

事實(shí)上，滿(mǎn)足上述條件的點(diǎn)A,B又稱(chēng)為圓O的一對(duì)反演點(diǎn).

例2 (2014湖北高考題)已知圓O:x2+y2=1和點(diǎn)A(-2,0)，若定點(diǎn)B(b,0)(b≠-2)和常數(shù)λ滿(mǎn)足：對(duì)圓O上任意一點(diǎn)M，都有|MB|=λ|MA|，則(1)b= ；(2)λ= .

圖4

點(diǎn)評(píng)：解法1是基本的方法，解法2要求更高，更簡(jiǎn)潔，做小題更迅速，可以節(jié)省時(shí)間，此題告訴我們，已知阿波羅尼斯圓的一個(gè)定點(diǎn)，可求得另一個(gè)定點(diǎn)及圓上任一點(diǎn)到兩個(gè)定點(diǎn)所成的比.

例3 (2015湖北高考題)如圖4，圓C與x軸相切于點(diǎn)T(1,0)，與y軸正半軸交于兩點(diǎn)A,B(B在A的上方)，且|AB|=2．

(1)圓C的標(biāo)準(zhǔn)方程為 ；

其中正確結(jié)論的序號(hào)是 .(寫(xiě)出所有正確結(jié)論的序號(hào))

易得正確結(jié)論的序號(hào)為①②③.

點(diǎn)評(píng)：對(duì)阿波羅尼斯圓的逆用，先判斷得出A,B是它的兩個(gè)定點(diǎn)，可快速解決本題.

圖5

命題2 如圖5，MN是圓O的一條直徑，A是直線(xiàn)MN上異于O的一個(gè)定點(diǎn)，過(guò)點(diǎn)A任作一條異于MN的直線(xiàn)交圓O于P,Q兩點(diǎn)，點(diǎn)P關(guān)于直線(xiàn)MN的對(duì)稱(chēng)點(diǎn)為P′，直線(xiàn)P′Q與MN交于點(diǎn)B，則A,B是圓O的一對(duì)反演點(diǎn).

證明：連接QO與圓交于點(diǎn)C，連接P′C,由Q,P,P′,C四點(diǎn)共圓得∠QPP′=∠QCP′，又∠OAQ+∠APP′=∠OQB+∠QCP′=90°,所以∠OAQ=∠OQB,從而ΔOAQ～

圖6

|OA|·|OB|=|OQ|2=r2.

特別地,如圖6，過(guò)A作圓O的兩條切線(xiàn)，切點(diǎn)分別為P,Q，連接PQ，與MN相交于點(diǎn)B，則A,B是圓O的一對(duì)反演點(diǎn).

圖7

命題3 如圖7，P為異于M,N的以A,B為定點(diǎn)的阿波羅尼斯圓上一點(diǎn)，則PM、PN分別為∠APB的內(nèi)、外角平分線(xiàn).

圖8

例4 (2001中國(guó)西部數(shù)學(xué)奧林匹克題)如圖8，過(guò)圓O外一點(diǎn)P作其切線(xiàn)PA,PB，OP與圓O和AB分別交于點(diǎn)I,M，DE為過(guò)M的任意弦.求證：I為ΔPDE的內(nèi)心.

證明：由命題2知，M,P為圓O的一對(duì)反演點(diǎn)，連接EI,DI，由命題3得，EI,DI分別為∠PED，∠PDE的角平分線(xiàn)，所以I為ΔPDE的內(nèi)心.

點(diǎn)評(píng)：如能巧妙地運(yùn)用阿氏圓的相關(guān)知識(shí)來(lái)處理，有時(shí)就能縮短思維路徑，簡(jiǎn)化解題過(guò)程，起到事半功倍的效果!

將圓通過(guò)伸縮變換變?yōu)闄E圓，則可得到如下結(jié)論：

圖9

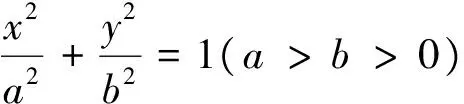
圖10

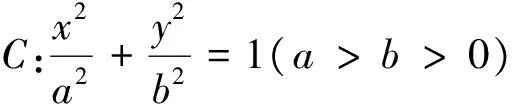
n)(m≠0)都在橢圓C上，直線(xiàn)PA交x軸于點(diǎn)M．

(1)求橢圓C的方程;

(2)設(shè)O為原點(diǎn)，點(diǎn)B與點(diǎn)A關(guān)于x軸對(duì)稱(chēng)，直線(xiàn)PB交x軸于點(diǎn)N．問(wèn)：y軸上是否存在點(diǎn)Q，使得∠OQM=∠ONQ？若存在，求點(diǎn)Q的坐標(biāo)；若不存在，說(shuō)明理由．

(2)假設(shè)y軸上存在點(diǎn)Q，使得∠OQM=∠ONQ，則RtΔOQM與RtΔONQ相似,所以|OM|·

點(diǎn)評(píng)：將圓的性質(zhì)通過(guò)仿射變換，得到橢圓的類(lèi)似性質(zhì)，是命題者常用的一種手段.

有了對(duì)阿波羅尼斯圓的系統(tǒng)認(rèn)識(shí)，像以上所舉的幾個(gè)問(wèn)題，認(rèn)清問(wèn)題的本質(zhì)，我們就能很輕易的解決，在我們學(xué)習(xí)中要善于對(duì)各種題型歸類(lèi)，深入探究.作為教師，我們要善于挖掘問(wèn)題的本質(zhì)和背景，站在更高的角度去理解問(wèn)題，這樣更有利于提高教學(xué)質(zhì)量，促進(jìn)學(xué)生創(chuàng)造性思維的發(fā)展.

[1]楊煉.阿波羅尼斯圓的新性質(zhì)及應(yīng)用[J].中學(xué)數(shù)學(xué)雜志，2016(5).

[2]孫明.例析2015年高考解析幾何試題的反演點(diǎn)背景[J].高中數(shù)學(xué)教與學(xué)，2015(10).

[3]徐梅香.由阿波羅尼斯圓衍生的橢圓性質(zhì)[J].中學(xué)數(shù)學(xué)月刊，2014(6).