LabVIEW輔助設計數字濾波器及FPGA實現

張文濤，張鵬蛟，趙 鵬

（長安大學，陜西 西安 0300511）

在輻照加速器低電平控制系統中，從加速腔中采集的信號受到外界的干擾信號的影響，為保證整個控制系統正常運行，并保證整個系統最低要求的精度，因此具有高精度、實時的數字濾波器的設計被提出來。數字濾波器的實質是對數字信號的運算處理，從而改變原始信號，完成濾波處理，得到要求的信號。通常模擬濾波器對濾波器元件精度要求比較嚴格，而且后面調試也比較耗時，且可靠性較低，相比起來，數字濾波器的可靠性和穩定性都很高，且容易調節，即只要改變濾波器的參數就可以很方便的改變濾波器的性能，直到達到要求[1]。

早期，為了解決濾波器的實時性和高計算速率問題，通常的辦法是采用專用的高速數據處理芯片和匯編語言來完成程序編寫，但是這樣，一方面對硬件成本要求提高，另一方面設計周期會延長，并且芯片的存儲量也對濾波器的設計有不小的影響。而大型可編程門陣列（FPGA）具有高速運算速度，大的存儲量，可編程，用戶易操作，從而大大地節省了設計成本和縮短設計周期。通過FPGA和LabView的聯合使用，進一步提高設計速度和可靠性[2]。

1 FIR濾波器的原理

FIR濾波器，也就是有限沖擊響應濾波器，字面上不難理解，也就是說，該濾波器一個單位響應脈沖是有限的。詳細地來講，FIR濾波器其突出特點是使其單位取樣響應h（n）是一個N點長的有限長序列0～N-1.這樣濾波器的輸出y（n）可表示為輸入序列x（n）與單位取樣響應h（n）的線性卷積。其表達式如下。

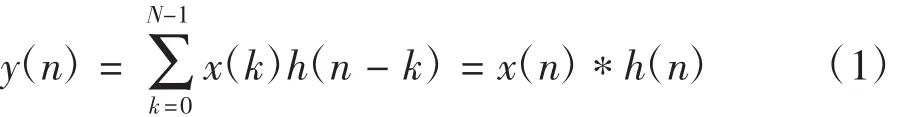
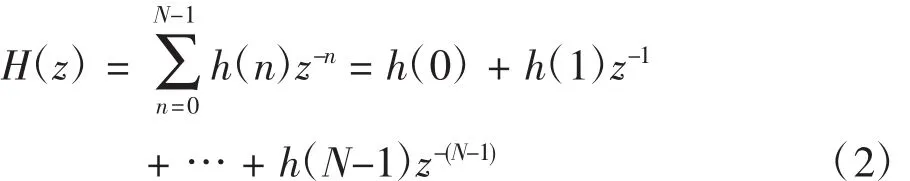
從上面系統函數不難發現，FIR濾波器的極點只存在原點上，這使得FIR系統具有全局穩定性。另外分析其函數右邊組成可知FIR濾波器可以看成加法器和乘法器組合而成，每個乘法器都有一個操作系數，也就是通常所說的抽頭次數，這些抽頭系數可以通過相關軟件計算獲得。這也是這種濾波器結構被人們稱為“抽頭延遲線結構”的原因。

1.1 FIR濾波器結構選擇

大體來講，根據不同場合要求有四種FIR的基本結構，根據不同的要求來供選擇，即直接型、快速卷積型、頻率取樣型和級聯型四種濾波結構。考慮到實現的復雜性，運算的存儲量和FPGA實現的難易程度，因此，這里選擇直接型FIR濾波器結構。FIR濾波器的輸出y（n）可表示為輸入序列x（n）單位取樣響應h（n）的線性卷積，根據式（1）和（2）可以很容易得出FIR濾波器的直接型結構（假設濾波器的單位取樣響應為M+1點長的有限序如圖1所示[3]。

其系統函數為

圖1 直接型FIR濾波結構

通過上面結構來看，就M+1階的FIR濾波器，要有M+1個乘法運算單元和M個用來的延時單元，另外還要一個加法運算單元用來整合。由于通過FPGA完成上述結構過程中，乘法運算所耗器件資源要比加減法等運算所耗費資源多得多。因此在實際情況實現時，需要最大程度降低乘法運算量。由FIR濾波器相關結構特點，很容易知道，只有單位取樣響應具有對稱特性的FIR濾波器才具有線性相位特性，所以，一般都會使用具有線性相位特性結構的濾波器來實現FIR濾波器，著重點就是其對稱特性，這樣就省去了很大一部分器件資源。

根據FIR濾波器的幅度特性，可以將濾波器分成四種不同的結構，根據不同的結構，也分別對應了相應的直接型FIR濾波器基本結構。對于第一種結構，即M是偶數，且單位取樣響應為偶對稱的情況，對其系統輸入與輸出關系式如下所示。

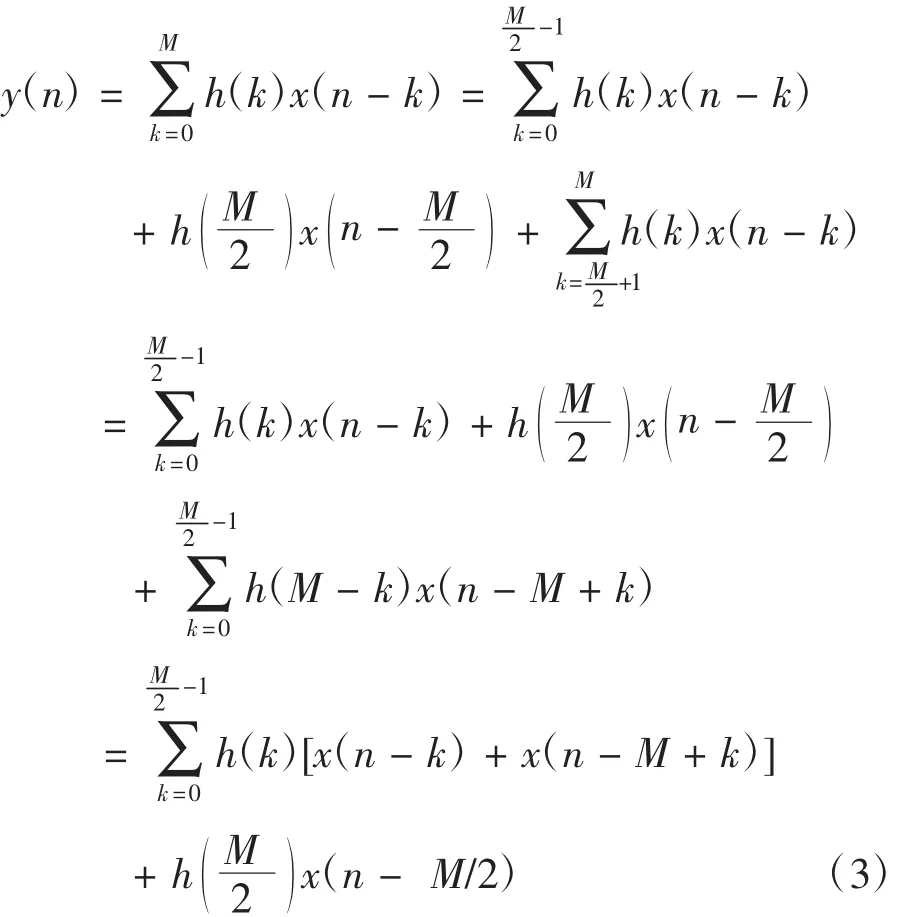
同樣的方法，也可以得出其它幾種結構系統的輸入與輸出響應關系。對于第二種結構，即M是奇數，單位取樣響應為偶對稱的情況，系統輸入與輸出關系式如下所示

第三種結構，即M是偶數，單位取樣響應為奇對稱的情況，系統輸入與輸出關系式如下所示。

第四種結構，即M是奇數，單位取樣響應為奇對稱的情況，系統輸入與輸出關系式如下所示

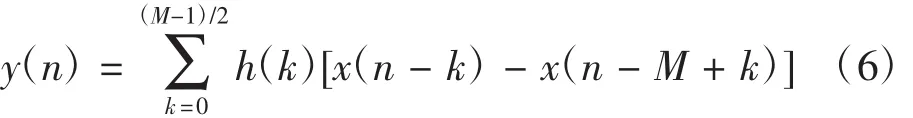
根據式（3）、式（4）、式（5）、式（6），可以分別畫出響應的實現結構，這里給出第二種對稱機構的FIR濾波器結構如圖2所示。

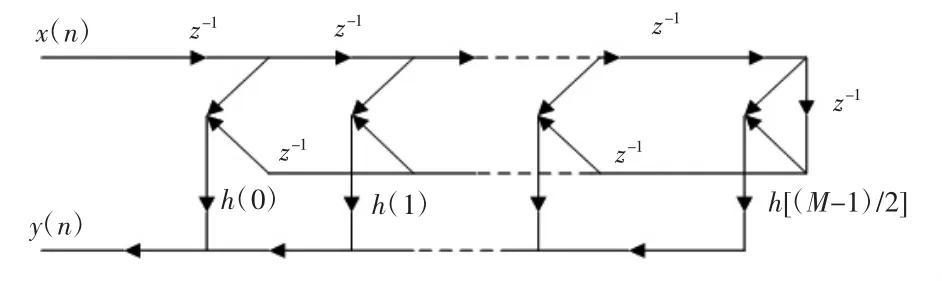
圖2 線性相位FIR濾波器的直線型結構

通過觀察圖1和圖2所示的兩種濾波器結構不難分析可以得出，對于相同階數的系統，使用線性相位的濾波器要比使用非線性相位的FIR濾波器所需要的乘法運算操作至少降低了一半，這樣一來就可以很有效的降低對FPGA內部資源的使用。

1.2 FIR數字濾波器設計

FIR濾波器抽頭系數h（i）設計方法有多種，有窗函數法（從時域角度出發）、頻率取樣法（從頻域角度出發）、最優設計方法（等波紋切比雪夫逼近法），其中窗函數法設計最簡便。Kaiser窗是一種可調窗，是利用I0（x）即等零階貝塞爾函數構成的，Kaiser窗函數的表達式為。

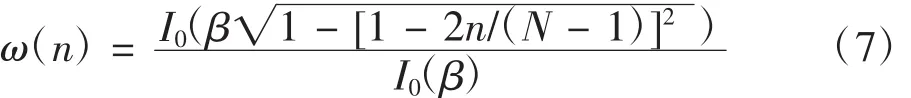
式中，I0（x）是第一類變形貝塞爾函數；β是窗函數的形狀參數，可以自由選擇。改變β值可以調節主瓣寬度和旁瓣電平，β＝0時相當于矩形窗，其典型值為4～9[4].

2 濾波器設計的前仿真

LabView有圖形化表示的脈沖函數和正弦函數，強大的數據分析模塊、圖形語言和交互界面。程序編制模塊由下而上，層層調用子程序，設計的交互界面調試方便。本設計待處理的信號是一個1 MHz正弦信號和2 MHz正弦信號的疊加信號，采樣率為32 MHz，濾波器階數為64階。圖3濾波器設計的頻譜圖。

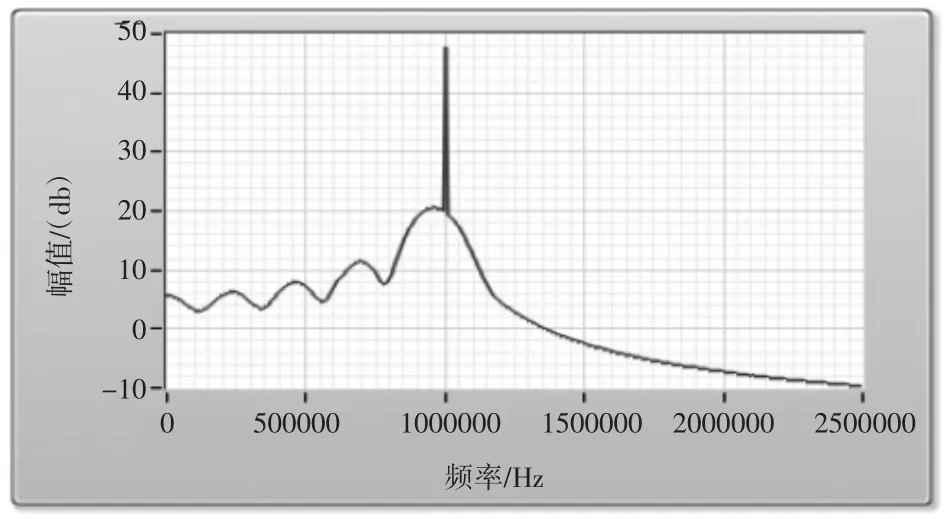
圖3 FIR濾波器的頻譜圖

從圖3可以看到，顯然1 MHz信號在通帶內，而2 MHz信號在通帶以外，被衰減掉了。下面圖4、5和6是濾波器通過疊加信號之后的頻譜圖和時域波形，很明顯2 MHz信號被有效地濾除掉了。

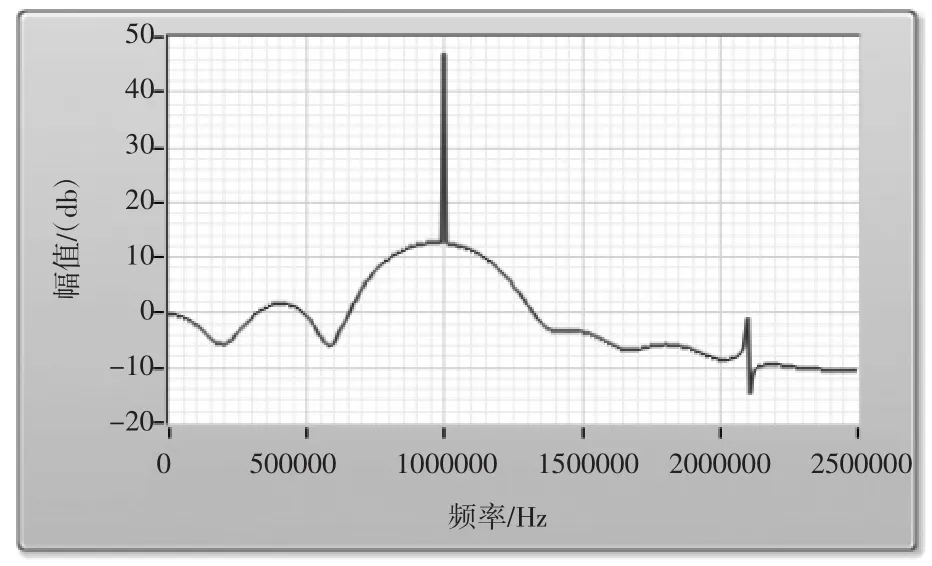
圖4 LabVIEW中疊加信號通過濾波器的頻譜圖

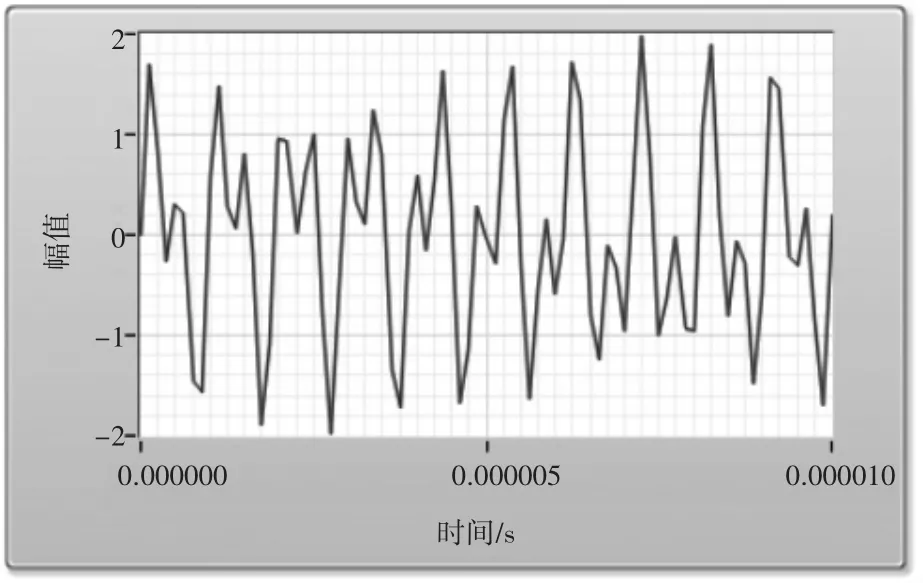
圖5 LabVIEW中疊加信號通過濾波器前的時域圖

圖6 LabVIEW中疊加信號通過濾波器后的時域圖

3 通過FPGA的濾波器實現

FPGA（Field-Programmable Gate Array），即現場可編程門陣列，它是在PAL、GAL、CPLD等可編程器件的基礎上進一步發展的產物。它是作為專用集成電路（ASIC）領域中的一種半定制電路而出現的，既解決了定制電路的不足，又克服了原有可編程器件門電路數有限的缺點。本次設計采用的是Altera公司Cyclone IVE系列芯片，利用QuartusⅡ11.0編輯環境進行設計，QuartusⅡ11.0編輯軟件中提供了大量現成可直接調用的IP核如加法器、乘法器等，大大的縮短了設計所需的時間。圖7是具有線性相位的并行FIR濾波器結構圖，以此為根據來編寫FPGA程序[5]。

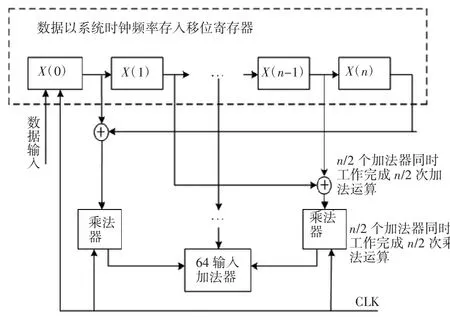
圖7 具有線性相位的并行FIR濾波器結構

上述并行結構，即并行實現濾波器的累加運算，具體來講就是將具有對稱系數的輸入數據進行相加，而后采用多個乘法器并行實現系數與數據的乘法運算，最后將所有乘積結果相加輸出。可以看出，這種結構具有最高的運行速度，由于不需要累加運算，因此系統時鐘頻率可以與數據輸出時鐘頻率一致。

4 FPGA設計實現后仿真測試

本次FIR濾波器FPGA設計仿真測試由Modesim仿真軟件來完成，這是因為其有比較友好交互環境，仿真速度快，保護IP核不受影響，并且同時支持VHDL和Verilog HDL語言。仿真結果由圖8所示。

圖8 FIR濾波設計ModelSim仿真時序圖

由圖8可以看出，濾波器輸入信號（Xin）的波形由于是頻率1 MHz和2.1 MHz正弦波的合成信號，從時域上無法明顯分辨出1 MHz信號，由于濾波器輸出信號（Yout）是經過低通濾波后的信號，可以明顯的看出2.1 MHz正弦波信號被濾除，保留了1 MHz正弦波信號，輸出信號起始處波形是一小段直流分量，這是由于FIR濾波器運算時產生的固有延時造成。根據FIR濾波器原理，長度為N的濾波器，濾波延時為N/2個數據周期。

將上述濾波器輸出信號上傳給LabView，經過處理可得到圖9.

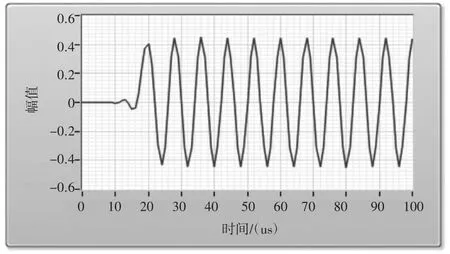
圖9 LabVIEW接收FPGA輸出數據的時域圖

由此可以通過LabView對比FPGA設計FIR濾波前后數據以達到對比的效果

5 結束語

本次設計首先通過LabView完成FIR濾波器設計的前期仿真，并得到FPGA設計所需要的抽頭系數，然后使用VerilogHDL硬件描述語言完成FPGA的設計，接著將從FPGA輸出的數據傳輸到LabView中，實現上位機和下位機的友好交互，已達到對濾波效果的實時檢測。通過上述仿真結果證實上述方案的可行性。

參考文獻：

[1]杜 勇.數字濾波器的MATLAB與FPGA實現[M].北京：電子工業出版社，2015：105-144

[2]姜碧瓊，盧博友，雷永鋒，等.基于LabVIEW7.0的數字濾波器設計[J].微計算機信息，2008，24（10）：173-174.

[3]李澤明，李錦明.FIR數字濾波器的MATLAB輔助設計及FPGA實現[D].太原：中北大學，2013.

[4]蔡 興，唐 求.基于LabVIEW的多采樣率數字濾波器1/3倍頻程計算方法[D].長沙：湖南大學，2015.

[5]夏雨文.Verilog數字系統設計教程[M].3版.北京：北京航空航天大學出版社，2013：97-110.