高速機器人的分數階終端滑模跟蹤控制

田雪虹，劉煥牢，劉海濤

（廣東海洋大學機械與動力工程學院，廣東 湛江524088）

0 引言

隨著用戶對機器人的要求越來越高，傳統的PID控制已無法滿足要求，許多非線性控制方法得到越來越多的重視，如自適應控制、滑模變結構控制、迭代學習控制、反步控制、神經網絡控制等等。這些控制方法各有優勢，也存在不足，在實際應用中具有一定的局限性。本文是針對高性能的工業機器人系統，其控制要求是高速、強魯棒性和高抗干擾力，而以上方法難于滿足性能要求。

有些研究表明系統的有限時間穩定比漸近穩定具有更好的控制精度和抗擾動性能[1]，因而得到研究者的密切關注，常見的有限時間控制方法有時間最優控制[2-3]、終端滑模控制[4-5]、齊次性方法[6]等。終端滑模控制是通過設計一種動態非線性滑模面方程實現的，并使得滑模面誤差能夠在有限時間能收斂到零[7-8]。因此，該控制方法在很多系統的控制設計中被廣泛應用。文獻[9-10]考慮集群航天器電磁編隊系統的強非線性特性，結合非奇異終端滑模理論，提出了一種有限時間穩定性控制方法。文獻[11]提出了一類自適應終端滑模有限時間控制方法顯式地引入輸出的飽和幅值，確保閉環系統在有限時間內快速收斂到滑模面的鄰域內。但是傳統的終端滑模控制存在切換特性，容易使系統產生“抖振”現象。為解決“抖振”問題，張碧陶等[12]將分數階理論引入到滑模面中，從而有效的削減了抖振。在此基礎上文獻[13]將分數階理論與模糊邏輯相結合，提出了基于模糊分數階的滑模控制策略，同樣能有效地削減抖振，并且能保持滑模控制器對系統外部擾動的全局魯棒性。文獻[14]針對機器人實際存在的不確定性問題，提出了基于神經網絡的分數階滑模控制方法，采用BP神經網絡逼近機器人的逆動力學方程并進行補償，因而具有良好的魯棒性。但是以上方法無法獲得閉環系統的有限時間穩定性。基于此，本文為進一步提高機器人的控制性能，將分數階理論推廣至終端滑模控制理論，從而保證系統在有限時間收斂的同時能夠消減抖振。

1 問題的描述

考慮具有n自由度的多輸入多輸出的工業機器人系統：

其中 q，q˙，q¨∈Rn分別是關節角度、角速度和角加速度向量，M（q）∈Rn×n為對稱正定的慣性矩陣，C（q，q˙）∈Rn×n是哥氏力和向心力矩陣，G（q）∈Rn是重力項，τ∈Rn為各關節的控制力矩。

實際上很難甚至不可能精確獲得模型（1）的動力學參數，因此基于動力學的控制方法需要考慮這些參數不確定性對機器人性能的影響。為此，本文將機器人的實際參數表達為如下形式

其中 M0，C0，G0為估計參數，△M，△C，△G 為參數的未知部分。則機器人的動力學方程（1）可表達為

其中，

ρ（q¨）∈Rn稱為機器人參數的不確定性函數。

假設1.不確定性函數滿足：

其中ε＞0，由于機器人的關節加速度是有上限的，因而假設1是符合實際的。

2 分數階終端滑模控制

考慮一類帶不確定性的二階非線性系統：

其中x=[x1，x2]T，非線性函數f（x）和g（x）≠0是平滑的，d（x）為未知不確定函數，滿足‖d（x）‖≤dˉ，dˉ＞0.

為了消除“抖振”，本文提出一種基于分數階理論的終端滑模方法，即選擇如下滑模面：

采用基于分數階的滑模面，本文得到如下定理：

定理 1針對系統（6），若選擇滑模面（7），將控制器設計為：

式中k＞d＞0，則系統狀態能在有限的時間內運動到TSM滑模面。

證明：

對滑模面（7）求導可得

選擇如下Lyapunov函數

對上式求導可得

將控制器（9）代入上式得

因此，由Lyapunov穩定性理論可知，系統狀態能在有限的時間內T到達滑模面。

為證明沿著滑模面的系統狀態到達平衡點的時間也是有限的，文獻[14]得到如下引理：

引理1[14]假設連續正定函數V（t）滿足微分不等式

式中μ＞0，0＜η＜1均為常數。則V（t）滿足不等式

V（t）≤V1-η（0）-μ（1-η）t 0≤t≤tr1（15）

并且 V（t）=0，?t≤ tr1，有限時間

在終端滑模s（t）=0上。由引理1可證明到達平衡點的時間也是有限的。

即由 s（t）=0 可得

定義Lyapunov函數為

V沿滑模面對時間求導有

其中 μ =2(1+λ)/2α，0 ＜ η =（1+ λ）/2 ＜ 1.由引理1 可知，當 t≥ tr1時，有 x1=0，且

說明：式（9）中的符號函數 sgn（s）也會造成“抖振”現象，故本文采用分數階導數的濾波特性來抑制“抖振”，即將 sgn（s）修正為：

證明：當采用分數階控制律時，可選擇如下Lyanpunov函數

對上式求導可得：

因此設計控制器為

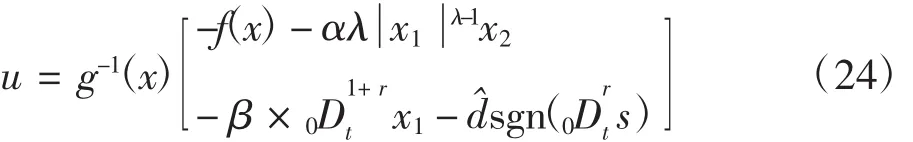
其中d^＞d＞0.則恒有V˙≤ 0，根據Lyapunov穩定性理論可知，系統能在有限的時間內運動到切換面.故得到以下定理：

定理 2針對系統（6），若設計滑模面為式（7），有限時間控制器設計為式（24），則系統狀態到達TSM滑模面的時間是有限的。

3 基于分數階的機器人終端滑模控制

工業機器人有限時間軌跡跟蹤控制的目的就是使機器人的關節q能有效地跟蹤期望的qd，且使跟蹤誤差 e 收斂至零的時間是有限的，其中 e（t），e˙（t）∈Rn分別定義為 x1=e=q-qd，x2=e˙=q˙-q˙d則機器人的動力學模型（3）可表達為：

若采用同式（7）的滑模面，則有以下定理。

定理2 針對系統（20），若選擇滑模面（7），且將控制器設計為：

證明類似于定理2，略。

4 仿真

為了驗證本文算法的有效性，本文對如圖1所示的高速二自由度機器人進行仿真，其動力學方程為

其中

m11=p1+p2+2p3cosq2-2p4sinq2

m12=p2+p3cosq2-p4sinq2

m22=p2

b=p3sinq2+p4cosq2

p1，p2，p3和 p4為機器人的最小慣性參數，d1=0.5sint，d2=0.5cost為機器人的外界干擾；機器人的實際參數值為：p1=0.049 8 kg·m2，p2=0.003 6 kg·m2，p3= －0.001 5 kg·m2，p4=0.008 1 kg·m2；而其估計參數值為：p1=0.038 6 kg·m2，p2=0.019 24 kg·m2，p3= －0.000 45 kg·m2，p4=0.004 923 kg·m2. 機器人的期望軌跡為qd1=sin2t，qd2=sin2t.系統的初始狀態為q1（0）=0.2 rad，q2（0）=0.2 rad，q˙1（0）＝0 rad/s，和q˙2（0）＝0 rad/s.控制器的控制參數為：α=diag（25，25，25），β =diag（20，20，20），w=diag（30，30，30），r=0.8，λ =0.8.

圖1 兩自由度平面機器人

仿真結果如圖2、圖3所示，由圖2可以看出這些關節的響應時間在1 s左右，且各關節的位置跟蹤誤差為0.05 rad，容易得出，本文提出的算法具有較高的跟蹤精度、較快的瞬態特性和較強的魯棒性。由圖3可以看出，各軸的控制量相對平滑，也不存在抖振現象。

圖2 機器人的跟蹤誤差

圖3 各關節的控制輸入量

5 結論

本文針對傳統整數階終端滑模控制系統的抖振問題，提出了分數階的終端滑模控制算法。通過采用分數階的切換流形來抑制抖振，再結合終端滑模控制的有限時間收斂特性，從而保證機器人閉環系統具有較高的跟蹤精度、較快的瞬態特性和較強的魯棒性。仿真結果表明，本文提出的控制方法是有效的、可行的。

參考文獻：

[1]Shihong DING，Shihua LI，Qi LI.Stability analysis for a second-order continuous finite-time control system subject to a disturbance[J].J of Control Theory and Applications，2009，7（3）：271-176.

[2]于瑞林，郭 磊.一類有限時間切換系統的最優制問題[J].控制理論與應用，2010，27（8）：1093-1096.

[3]甄子洋，江 駒，王志勝，等.有限時間信息融合線性二次型最優控制[J].控制理論與應，2012（2），29（2）：172-176.

[4]Shihong Ding，Shihua Li.Stabilization of the attitude of a rigid spacecraft with external disturbances using finite-time control techniques[J].Aerospace Science and Technology，2009（13）：256-265.

[5]Jin Erdong，Sun，Zhaowei.Robust controllers design with finite time convergence for rigid spacecraft attitude tracking control[J].Aerospace Science and Technology，2008（12）：324-330.

[6]Hua Wang，Zhengzhi Han，QiyueXie，Wei Zhang.Finite-time chaos control of unified chaotic systems with uncertain param eters[J].Nonlinear Dynamics，2009，55（4）：323-328.

[7]丁世宏，李世華.有限時間控制問題綜述[J].控制與決策，2011，26（2）：161-169.

[8]丁世宏，李世華，羅 生．基于連續有限時間控制技術的導引律設計[J].宇航學報，2011，32（4）：727-733.

[9]胡 敏，曾國強.基于終端滑模的集群航天器電磁編隊有限時間控制[J].航天控制，2011，29（6）：22-27.

[10]胡 敏，曾國強.衛星編隊飛行有限時間控制方法[J].空間控制技術與應用，2012，38（1）：23-28.

[11]胡慶雷，李 波，張愛華，等.考慮推力器安裝偏差的航天器姿態機動有限時間控制[J].控制理論與應用，2013，30（4）：417-424.

[12]張碧陶，皮佑國.基于分數階滑模控制技術的永磁同步電機控制[J].控制理論與應用，2012，29（9）：1193-1195.

[13]張碧陶，皮佑國.永磁同步電機伺服系統模糊分數階滑模控制[J].控制理論與應用，2012，27（12）：1776-1780.

[14]Yu T.Terminal sliding mode control for rigid robots[J].Au tomatica，1998，34（1）：51-56.

[15]徐慶宏，黃家才，周 磊.基于神經網絡逆系統的機器人分數階滑模控制[J].組合機床與自動化加工技術，2015（12）：49-52.