基于博弈論的軌道交通建設項目安全投入與監管行為分析

畢樹柏，宮本福

(1.中國安全生產科學研究院，北京 100012；2.北京市軌道交通建設管理有限公司，北京 100071)

0 引言

隨著城市規模的不斷擴展，地面交通已經遠遠不能滿足大規模人群出行的需求，地鐵作為一種重要的軌道交通工具，因其快速、準時、大容量的特點，已經成為城市居民出行的最主要交通工具之一。截至2017年上半年，中國內地已有31個城市開通運營城市軌道交通，運營總里程共3 965 km[1]。以北京為例，到“十三五”末，全市軌道交通將形成“三環四橫八縱十二放射”軌道交通網，總里程提高到900 km以上，將實現區區通軌道，中心城區軌道交通750 m站點覆蓋率達到90%[2]。雖然快速發展的城市軌道交通帶給人們出行便利，但城市軌道交通建設本身是一項復雜的高風險性系統工程, 其建設過程中帶有很大不確定性, 尤其隨著項目建設進程的推進, 新建隧道往往要近鄰既有地下基礎設施及地上建( 構) 筑物施工, 必然會對其安全造成不利影響, 若控制不力極易造成重大安全事故。如2003年7月1日凌晨，上海軌道交通4號線越江隧道區間用于連接上、下行線的安全聯絡通道——旁通道工程施工作業面內，大量的水和流沙涌入，引起隧道部分結構損壞及周邊地區地面沉降，造成3棟建筑物嚴重傾斜，黃浦江防汛墻局部塌陷并引發管涌，直接經濟損失約1.5億元[3]；2007年3月28日，10號線蘇州街東南出入口發生塌方事故，導致地面嚴重塌陷，造成6名工人死亡[4]；2008年11月15日下午3時15分，正在施工的杭州地鐵湘湖站北2基坑現場發生大面積坍塌事故，造成21人死亡，24人受傷(截止2009年9月已先后出院)，直接經濟損失4 961萬元[5]。以上施工過程中發生的生產安全事故造成了重大人員傷亡和經濟損失，引起廣大科研與專業技術人員的關注，眾多學者從管理和技術等多個角度開展針對性研究，國家也逐年加大了對安全生產的監管力度，不但加強了問責、罰款等處罰力度，而且不斷強調企業對安全投入的重視。但企業作為市場經濟的獨立個體，經濟效益仍是大多企業的首要考慮，故如何把握好安全監管、安全投入與企業正常經營行為之間的關系，是急需解決的問題。博弈論作為一門研究不同主體策略相互作用的學科，可以通過嚴格的數學模型對這些問題進行規范描述，在統一框架下加以嚴整的數學分析[6]，進而得出更加合理的策略建議。如王永剛等[7]通過對我國民航安全監管模式的研究，探索政府安監部門對航空公司的安全監管策略，建立了不完全信息狀況下民航安全監管的進化博弈模型；張飛漣等[8]建立了建設項目安全監察機關與施工單位之間的安全管理博弈模型；程敏等[9]在建筑企業與政府安全監管部門僅具有有限理性的前提下，運用演化博弈方法對建筑工程安全監管過程中，建筑企業安全生產策略選擇與政府監管部門監管策略選擇的互動行為及穩定狀態進行了分析。通過對以上已有研究成果的分析，發現利用博弈論理論和模型進行相關安全監管模式分析已經在多個行業得到應用，但大多是圍繞基本的博弈模型建立與分析討論，得出的結論與措施建議也較為宏觀，缺少實際的行業或企業數據支持，進而在實際應用于相關安全監管和安全投入決策時，缺少良好的操作性。本文在此背景下，圍繞軌道交通建設項目相關的行業和企業特點，采用博弈論的理論和方法，剖析軌道交通建設施工企業自身的安全投入行為與安全監管部門的監管行為之間的關系，并以某企業的實際數據為例，進一步深入分析安全監管穩定狀態與施工企業的安全投入、事故后企業損失、監管部門執行安全監管的成本、企業違規受到的處罰力度、監管部門由于失職受到的處罰等因素之間的數量關系，并從施工企業安全投入與監管部門的措施建議方面給出建議，為軌道交通建設行業或企業的安全監管提供策略參考。

1 軌道交通建設項目安全投入與安全監管的博弈模型構建

1.1 理論基礎

博弈論研究的是不同人或團體等利益主體之間在利益相互制約下策略選擇時理性行為及相應結局，John[6]則認為博弈論是關于策略相互作用的理論，是關于社會形勢中理性行為的理論，其中每個局中人對自己行動的選擇必須以他對其他局中人將如何反應的判斷為基礎。從以上博弈論的定義以及理解來看，博弈論是對現實社會生活不同利益主體在爭取自身利益最大化過程中所采取的策略研究。從現實博弈行為中抽象出的參與人、策略和收益等3個基本要素共同構成了策略型博弈模型。其中：

1)參與人是指博弈的參與者，是相關策略采用或執行的決策主體，具體對應到現實生活中，可以是不同的人、企業或政府等。

2)策略是指可供參與人選擇采用的方案，每個參與人具有多種策略可供選擇；某個參與人所能夠選擇的多個策略共同構成了該參與人的策略空間；多個參與人根據自身判斷選擇1個策略后，形成的策略向量稱為策略組合。

3)收益是指各種策略組合下不同參與人獲得的收益，可以用策略組合的函數表示。

根據對所有參與人的策略空間和收益函數的了解情況，將策略型博弈分為完全信息博弈和不完全信息博弈；根據不同參與人在選擇策略時是否知道其他參與人的策略選擇，將策略型博弈分為靜態博弈和動態博弈。本文研究的企業安全投入與監管部門的安全監管博弈行為可以定義為完全信息下的靜態博弈。

1.2 博弈行為分析與博弈模型建立

改革開放以來，隨著我國國民經濟的快速發展，人民生活水平得到不斷提高，但隨著近年生產安全事故的頻發，各級政府及行業監管部門意識到安全、可持續發展的重要性，而強化安全監管以及加大安全投入均是目前有效的手段(策略)。在此背景下，從博弈論相關理論假設角度，監管部門和項目施工企業成為圍繞各自利益開展博弈的2個參與人。其中，監管部門作為完全理性的參與人，有2個純策略可供其選擇，分別為：執行安全監管(可以理解為執行100%的事故監管行為)和不執行安全監管(可以理解為執行0%的事故監管行為)，但實際監管活動中，監管部門大多不會選擇以上某個純策略，而更可能是執行在以上純策略基礎上形成的混合策略，即監管部門在實際博弈時，以某種概率分布在純策略中隨機選擇加以實施；項目施工單位作為完全理性的參與人，有2個純策略可供其選擇，分別為：按規定安全投入(可以理解按照監管部門的要求進行安全投入，涉及相關的人、財、物等方面)和不按規定安全投入(可以理解為不按照監管部門的要求進行安全投入，涉及相關的人、財、物等方面)，但實際項目建設過程中，項目施工單位大多不會選擇以上某個純策略，而更可能是執行在以上純策略基礎上形成的混合策略，即項目施工單位在實際博弈時，以某種概率分布在純策略中隨機選擇加以實施。

在以上監管部門與項目施工單位的博弈行為分析基礎上，可以對2個完全理性參與人的收益進行測算，進而建立該博弈模型的支付矩陣。

1.2.1 監管部門收益測算

1)監管部門選擇執行安全監管策略

作為監管部門的本職工作，安全監管行為本身并不能帶來收益，但當項目施工單位不按規定安全投入時，會出現監管部門對項目施工單位進行處罰的情況，具體形式可能包括罰款、降級、拉入黑名單等，為了與其他策略行為在經濟數量層面進行比較，此處將不同的處罰形式均簡化為罰款，用p表示。因此，對于監管部門來說，當執行安全監管且項目施工單位按規定安全投入的情況下，其收益為0；當執行安全監管而項目施工單位不按規定安全投入的情況下，其收益為p。

2)監管部門選擇不執行安全監管策略

當監管部門選擇不執行安全監管時，節省了執行安全監管產生的成本，變成監管部門的收益，但如果項目施工單位不按規定安全投入造成事故，將會對監管部門進行處罰。因此，對于監管部門來說，當不執行安全監管而項目施工單位按規定安全投入的情況下，其收益為安全監管成本，用c表示；當不執行安全監管且項目施工單位不按規定安全投入的情況下，其收益為安全監管成本c減去受到的行政處罰f，用(c-f)表示。

1.2.2 項目施工單位收益測算

1)項目施工單位選擇執行按規定安全投入策略

在本博弈模型中，作為完全理性的參與人，項目施工單位視利益最大化為最終目標，故其所有行為都用最終的經濟收益進行衡量。假設項目給施工單位能夠帶來收益r，按照安全監管部門的規定進行安全投入用t表示。則對于項目施工單位來說，當其按規定安全投入時候，無論安全監管部門是否執行安全監管，其收益均為(r-t)。

2)項目施工單位選擇不執行按規定安全投入策略

當項目施工單位選擇不執行按規定安全投入的策略，雖然節省了按照安全監管部門的規定所進行的安全投入t，但其面臨事故損失s和可能發生的監管部門罰款p。因此，對于項目施工單位來說，當不按規定安全投入且監管部門執行安全監管時，其收益為(r-s-p)；當其不按規定安全投入而監管部門不執行安全監管時，其收益為(r-s)。

1.2.3 博弈模型的支付矩陣

根據上文的博弈行為與不同參與人的收益測算，建立本文博弈模型的支付矩陣，如表1所示。

表1 支付矩陣

如表1所示，參與人①—監管部門的純策略包括：{s11:執行安全監管、s12:不執行安全監管}；參與人②—項目施工單位的純策略包括：{s21:按規定安全投入、s22:不按規定安全投入}，同時2個參與人均知道對方的策略空間和收益函數，但彼此不知道對方的具體選擇，屬于完全信息靜態博弈。

2 混合策略納什均衡的求解及分析

根據上文建立的博弈策略模型，對參與人①和參與人②采用混合策略條件下的參與人收益進行求解，用U(i)表示參與人i的收益，i=1,2；設參與人①執行策略s11的概率為x，則執行策略s12的概率為(1-x)；參與人②執行策略s21的概率為y，則執行策略s22的概率為(1-y)。

1)混合策略下的參與人①收益

U(1)=x×y×0+x×(1-y)×p+(1-x)×y×c+(1-x)×(1-y)×(c-f)=x(p-py-c+f-yf)+c+yf-f

(1)

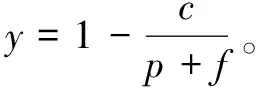
2)混合策略下的參與人②收益

U(2)=x×y×(r-t)+x×(1-y)×(r-s-p)+(1-x)×y×(r-t)+(1-x)×(1-y)×(r-s)=y(xp-t+s)+r-s-xp

(2)

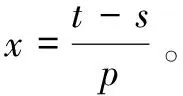
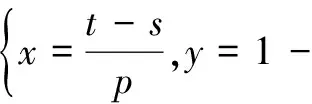
對以上形成的混合策略納什均衡作進一步的分析可知：監管部門執行“安全監管”的概率與項目施工單位按照規定進行的安全投入(t)、面臨事故損失(s)、監管部門對項目施工單位進行處罰(p)有關；而項目施工單位執行“按規定安全投入”的概率與監管部門執行安全監管的成本(c)、監管部門對項目施工單位進行處罰(p)、監管部門受到的行政處罰(f)有關；無論是監管部門，還是項目施工單位，其有關策略的選擇均與項目給施工單位能夠帶來收益(r)無關。處在混合策略納什均衡狀態下的監管部門的監管策略選擇和項目施工單位的安全投入選擇是本文關注的重點，通過分析可知，在逐年增加安全監管投入(人、財、物的投入)的背景下，應該進一步加大監管部門對項目施工單位違規進行的處罰(p)力度，才可能使項目施工單位更偏重于按規定進行安全投入，與此同時，根據參與人①的收益函數可知，增加安全監管(c)投入，可以使參與人①獲得更大的收益。

3 實例分析

下文以某軌道交通建設項目為例，對上文的博弈模型與策略選擇進行舉例說明，并結合項目實際提出安全監管與安全投入方面的建議措施。

現有我國某市的城市軌道交通在建項目,該項目是該城市東西主干線，并對接與周邊城市的快軌通道,項目共分二期建設,其中一期項目共設9個標段,分別由相關具有資質的施工單位進行實施,每個標段的安全生產工作除了施工企業作為責任主體進行管理以外,該市城市軌道交通建設管理有限公司代表該市政府(出資方)進行綜合安全監管。本文以其中某個標段為例,對相關安全投入與監管行為進行分析說明。

1)施工單位的安全投入(t)

根據該標段約4.26 億元的總體工程投資額，施工單位的安全投入約為1 100萬元。

2)施工單位發生生產安全事故的損失(s)

根據國內其他同類施工條件下實際發生生產安全事故(基坑坍塌事故)造成的損失情況，估算該標段發生生產安全事故的損失約為300萬元，其中事故直接經濟損失約250萬元；發生事故后，監管部門對其的處罰約50萬元。

3)監管部門對施工企業進行監管時，發現違規后的罰款(p)

根據該市軌道交通建設管理有限公司的規定，發現每次施工企業違規后，所施加的罰款與違規的嚴重程度相關，但大多不超過10萬元/次。

4)標段給項目施工單位帶來的收益(r)

根據該表段的總體工程投資額，該值約為2 500萬元。

在以上該項目標段的數據基礎上，結合前文建立的安全投入與監管行為的博弈模型，分析結論如下：

4 結論

1)利用博弈論理論，建立軌道交通建設項目安全投入與監管行為的完全信息下的靜態博弈模型，并提出監管部門(參與人①)和施工單位(參與人②)的收益函數。

2)在相關參與人的收益矩陣基礎上，對博弈的混合策略納什均衡進行求解和分析，得出相應的策略組合。

3)以某市具體軌道交通建設項目為例，對相關博弈模型與策略選擇進一步分析，結果表明：相對該標段總體工程投資額(約4.26億元)，在整個施工周期中，監管部門需要施加的違規罰款力度(p)需要在800萬元以上，而隨著p的增大，監管部門能夠以更小的安全監管概率維持在均衡狀態，而此時對于施工企業來說，p的增大，會進一步督促施工企業提高安全投入概率；需要說明的是，本文所舉實例中，對事故可能造成的損失作了一定程度的簡化，僅以某次實際事故造成的經濟損失作為計算依據。

[1] 中國城市軌道交通網.我國城軌交通迎來大發展 ，31個城市開通城市軌道交通，總里程近4000公里[EB/OL].(2017-11-27)[2018-04-24].http://www.chinametro.net/index.php?m=newscon&id=410&aid=42504.

[2] 北京市人民政府.全市將形成“三環四橫八縱十二放射”軌道交通網 總里程超900公里[EB/OL].(2017-03-25)[2018-01-10].http://www.beijing.gov.cn/bmfw/zxts/t1472187.htm.

[3] 新浪網.上海軌道交通4號線事故直接經濟損失達1.5億元[EB/OL].(2003-09-20)[2018-01-10].http://news.sina.com.cn/c/2003-09-20/2209788546s.shtml.

[4] 侯艷娟, 張頂立, 李鵬飛.北京地鐵施工安全事故分析及防治對策[J].北京交通大學學報, 2009, 33(3):52-59.

HOU Yanjuan，ZHANG Dingli，LI Pengfei.Analysis of safety accident in Beijing subway construction and its prevention and control measures[J].Journal of Beijing Jiaotong University，2009，33(3)：52-59.

[5] 杭州網. 關于杭州地鐵湘湖站“11·15”坍塌重大事故調查處理結果的通報[EB/OL].(2010-02-09)[2018-01-10].http://ori.hangzhou.com.cn/ornews/content/2010-02/09/content_3050073.htm.

[6] 黃濤.博弈論教程:理論·應用[M].北京：首都經濟貿易大學出版社, 2004.

[7] 王永剛, 江濤.基于進化博弈論的不完全信息狀況下的民航安全監管研究[J].安全與環境學報, 2014, 14(1):61-64.

WANG Yonggang,JIANG Tao.On civil aviation supervision based on evolutionary game theory in absence of enough information[J].Journal of Safety and Environment,2014,14(1):61-64.

[8] 張飛漣, 劉力, 董武洲,等.博弈論在建設項目安全管理中的應用[J].系統工程, 2002, 20(6):33-37.

ZHANG Feilian,LIU Li,DONG Wuzhou,et al.The application of game theory in project safety management[J].Systems Engineering,2002,20(6):33-37.

[9] 程敏, 陳輝.基于演化博弈的建筑工程安全監管研究[J].運籌與管理, 2011(6):210-215.

CHENG Min,CHEN Hui.Research on construction safety supervision based on evolutionary game theory[J].Operations Research and Manacement Science，2011(6):210-215.