一種全面響應時間的頻率穩定度測量
許龍飛, 羅 丹, 周 渭, 白麗娜, 李智奇, 苗 苗
(西安電子科技大學 機電工程學院,陜西 西安 710071)
一種全面響應時間的頻率穩定度測量
許龍飛, 羅 丹, 周 渭, 白麗娜, 李智奇, 苗 苗
(西安電子科技大學 機電工程學院,陜西 西安 710071)
為從本質上反映不同頻率源的頻率穩定度隨響應時間的變化規律,提出了一種可以測量全面響應時間的頻率穩定度的方法.該方法在數字環境下,應用數字邊沿效應抑制量化誤差,并結合數字雙混頻時差法測量信號間的相位差,通過相位差得到全面的頻率穩定度指標.實驗證明,該方法在自校的條件下,100ns的頻率穩定度能夠達到10-5,秒級穩定度能夠達到10-12,一天的頻率穩定度能夠達到10-16.
數字化;量化誤差;雙混頻時差;頻率穩定度
頻率穩定度按照響應時間的大小分為瞬態頻率穩定度[1]、短期頻率穩定度和長期頻率穩定度.傳統的頻率穩定度測量方法有很多,例如有通過相位差測量的相位重合法、時間間隔測量和雙混頻時差法,有通過頻率測量的差拍法、頻差倍增法以及模擬內插法等[2-5].這些測量方法大都基于閘門計數,只能測量毫秒及以上的頻率穩定度,并且大都在模擬的環境通過計數閘門進行測量,雖然能達到一定的測量精度,但是存在單點過零檢測對噪聲較為敏感、對線路性能要求嚴格以及線路分辨率有限等問題,并且由于計數閘門無法太短,導致無法得到其更短時間的頻率穩定度指標,而這些更短時間的頻率穩定度的測量對于頻率源的抖動、實時短期不穩定度以及遠端相位噪聲的描述具有重要的作用.針對這些情況,筆者提出了在數字平臺下進行相位差測量的方法,將模擬信號通過模/數轉換器轉變成數字信號,對模/數轉換器的采樣時鐘頻率進行控制,使得到的數字信號具有數字模糊區,應用數字邊沿效應抑制量化誤差,并結合雙混頻時差算法得到信號間的相位差,進而得到頻率穩定度.將模擬信號轉換成數字信號之后,用的是鑒相算法,能得到信號間的相位差,彌補了模擬平臺下計數閘門無法太短的不足,因此能夠得到更加全面的頻率穩定度.對頻率源全面的頻率穩定度隨響應時間的變化規律掌握,可以從本質上區分頻率源的相位或者頻率控制,這也是對頻率源進行改進所必須要掌握的技術.

圖1 c=1時兩信號的相位變化關系
1 信號間的特殊相位關系
設兩信號的頻率分別為fA和fB,其中fB=cfA+ Δf(Δf?fA),隨著時間的延伸,兩信號間的相位關系有特殊的變化規律.c=1 時兩信號的相位差的變化規律如圖1所示.
圖1中Δt表示兩信號之間的相位差,Δt=TA-TB;Tmin為兩信號的最小公倍數周期[6].假設圖中初始時刻兩信號的上升沿完全重合,以后每經過一個TA,兩者的上升沿之間的距離會相對變化Δt,即兩者之間的相位差會增加或減少Δt,經過1個Tmin后,兩者之間的相位差累積成一個周期TB,這時兩比對信號的上升沿又會重新完全重合,并重復之前的變化規律.
若c≠1,則可將cfA看成一個整體,其變化規律可以歸結到c=1的情況.
2 數字邊沿效應和量化誤差的抑制
將信號間的特殊相位關系運用到模/數轉換器的采樣過程中,經過簡單的處理,能抑制很大一部分量化誤差.模/數轉換器的采樣分為過采樣和欠采樣,這里只詳述欠采樣.過采樣的原理和欠采樣的類似.
設模/數轉換器的位數為N位,測量量程為Ucc,則模/數轉換器的分辨率為Ucc/ (2N-1).設模/數轉換器的輸入信號y(t)=Ucsin(2πfAt+β(t)),采樣頻率為fB(fB=fA+ Δf,Δf?fA).模/數轉換器的采樣過程如下:
y(nTB)=Ucsin(2πfAnTB+β(nTB)) ,
(1)
其中,TB為采樣周期,TB=1/fB,n=1,2,3….將fB=fA+Δf代入式(1)中,得到
(2)
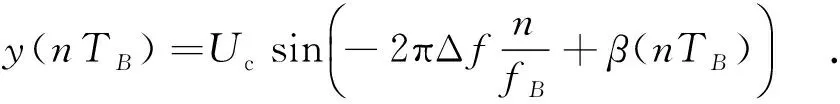
(3)
從式(3)中可以看出,模/數轉換器輸入的是頻率為fA的信號,經過模/數轉換器量化后,輸出的是頻率為Δf(Δf=fB-fA)的信號,這樣模/數轉換器相當于輸入為fA和fB的數字化的混頻器和低通濾波器.
結合信號間的特殊相位關系和模/數轉換器的采樣過程,每經過一個模/數轉換器的輸入信號周期TA,采樣時鐘信號和模/數轉換器的輸入信號的上升沿會相對拉開Δt,所對應的兩個采樣點之間的幅度增加Δu,Δu的大小為
Δu=y((m+1)TB)-y(mTB) ,
(4)
其中,m為大于零的正整數.式(4)化簡得到
Δu=y(mTB+TA-Δt)-y(mTB)=y(mTB-Δt)-y(mTB) .
(5)
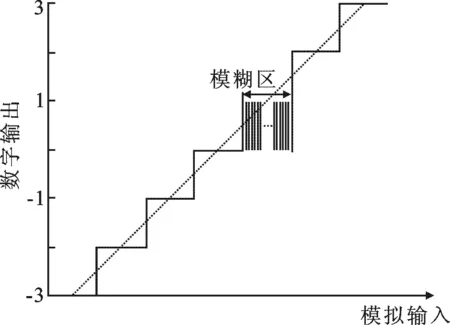
圖2 數字模糊區
如果Δu 圖2中的橫軸表示模/數轉換器的模擬輸入,縱軸表示模/數轉換器的數字輸出.由圖2可知,每個數字模糊區由許多個等間隔的量化值相同的點組成,每個模糊區中間都存在一個與真值相差最小的點.同一個數字模糊區中每兩個相鄰點之間的實際幅度大小相差Δu,因此,可以對模糊區中的點依次標號,模糊區的邊沿標號為1,其他依次增加,以這樣的方式補償來提高模/數轉換器的分辨率.或者直接取邊沿(跳變的點),加上一個固定的補償,這就是數字邊沿效應.利用數字邊沿可以取到真實值或者接近真實值的點,從而抑制量化誤差.這樣得到的數字信號雖然頻率與原信號不同,但是幅度與原信號一樣,僅僅是在橫坐標上相差一個倍數.如果將所有的點按照量化值依次重新進行排列,則可恢復出原信號. 在短期和長期頻率穩定度的測量中,并不需要取所有的采樣點進行量化誤差的處理,而是根據信號間最小公倍數周期的大小只取信號過零點附近的采樣點進行處理,原因是計算頻率穩定度并不需要每個采樣點的相位差,并且過零點區域的點不僅僅可以消除線性誤差,而且在過零點區域的點的變化斜率最大, 模/數轉換器所對應的相位分辨率最高.而在瞬態穩定度的測量過程中,可以使Δf盡量小,這樣就能保證在信號過零點附近有更多的采樣點. 傳統的數字雙混頻時差方法中存在數字混頻[7-8]、抽取濾波、直接數字合成器(Directed Digital Synthesizer,DDS)和鑒相等算法,處理流程十分復雜,而且會有精度損失.文中對雙混頻時差進行了改進,直接在模/數轉換器采樣過程中應用特殊頻率信號間的特殊相位規律進行量化和量化誤差處理,然后直接鑒相,得到信號間的相位差,系統如圖3所示.圖3中主要分為模擬部分和數字部分,模擬部分主要是模/數轉換器輸入通道的設計,主要實現對信號進行濾波和采樣以及消除噪聲干擾.在印制板走線上設計成差分對,布局上各通道之間相互對稱,可以降低噪聲干擾.數字部分的算法在現場可編程門陣列(Field Programmable Gate Array,FPGA)和單片機中實現.模/數轉換器輸出的數字信號先經過一個擬高斯濾波器[9],主要是消除一部分模/數轉換器的隨機噪聲,然后利用數字邊沿效應進行量化誤差的抑制.象限判斷用一個一定長度的先進先出的隊列實現,判斷隊列兩頭和中間數據的大小來判斷數據的象限.反正弦鑒相算法用查找表實現,因為實驗只取過零點區域的采樣點,因此可節約FPGA很大一部分邏輯資源.鑒相之后得到的是信號的角度,然后利用雙混頻時差原理得到兩信號之間的相位差,發送給單片機進行頻率穩定度的計算.根據前面所述,模/數轉換器可以作為一個數字化的混頻器和低通濾波器,因此,圖中的數字部分實際上是一個中介源為采樣時鐘的數字化的雙混頻時差系統. 圖3 頻率穩定度測量系統 假設被測信號yx(t)=Axsin(2πf0t+βx(t)),參考信號y0(t)=A0sin(2πf0t+β0(t)),時鐘采樣頻率fs=f0+ Δf(Δf?f0),根據上面所述,模/數轉換器相當于數字化的混頻器和低通濾波器,經過模/數轉換器采樣之后,模/數轉換器輸出頻率為Δf的數字信號,其瞬時相位分別為 (6) 根據雙混頻時差原理,得到被測信號和參考信號的相位差為 (7) 其中,Xx0為被測信號和參考信號之間的相位差,Xx0b為兩模/數轉換器輸出數字信號間的相位差,φx和φ0分別為被測信號和參考信號的瞬時相位,φxb和φ0b分別兩模/數轉換器輸出的數字信號的瞬時相位. 實驗采取圖3中的方案,模/數轉換器的分辨率為16 bit,以8607-BE 10 MHz OCXO晶振作為羅德史瓦茨SMB100A信號發生器的外部參考輸入,羅德史瓦茨SMB100A信號發生器產生 (10 MHz+ 10 Hz) 頻率的信號,作為 模/數轉換器的時鐘信號fs,1 s 以下的頻率穩定度用銣鐘輸出 10 MHz 信號作為被測信號,用8607-BE OCXO晶振輸出的 10 MHz 信號作為參考信號;1 s 以上的頻率穩定度用銫鐘輸出 10 MHz 信號作為參考信號,用銣鐘輸出 10 MHz 作為被測信號,模/數轉換器的采樣時鐘不變.實驗開始時,先分別利用特殊頻率信號間的特殊相位規律測出被測信號和參考信號的幅度,并儲存;然后利用數字模糊區的邊沿抑制量化誤差,用雙混頻時差法測出信號間的相位差,得到的頻率穩定度曲線如圖4所示. 圖4中縱坐標表示頻率穩定度,用阿倫方差表示.數據處理用計算頻率穩定度的專用軟件stable32進行.從圖4可以看出,100 ns 的穩定度能夠達到 2.92× 10-5,1 s 的穩定度能到達 1.82× 10-11.圖4中銣原子鐘的頻率穩定度曲線在 100 ns 和數十毫秒之間隨取樣時間呈 1/τ規律變化,數十毫秒以上的頻率穩定度變化規律隨著取樣時間就靠向了 1/τ1/2的變化規律.這是因為實驗中所用銣原子鐘中的晶體振蕩器本身的頻率穩定度是按照 1/τ的規律變化的,但是銣原子鐘存在一個調制信號,由于物理部分的鎖頻作用,在數十毫秒以上的頻率穩定度變化規律隨著取樣時間就靠向了 1/τ1/2的規律變化. 圖4 銣鐘的頻率穩定度圖圖5 高穩晶振自校頻率穩定度圖 以8607-BE 10 MHz OCXO晶振作為泰克信號發生器的外部參考輸入,泰克信號發生器產生 (10 MHz+ 10 Hz) 頻率的信號,作為模數轉換器(Analog to Digital Converter,ADC)的時鐘信號fs,參考信號和被測信號都采用8607-BE 10 MHz OCXO晶振輸出的 10 MHz 頻率信號,得到的結果如圖5所示. 圖5的數據處理用計算頻率穩定度的專用軟件stable32進行.在長期比對中,一天的頻率穩定度能到達 4.38× 10-16,并且隨取樣時間呈 1/τ規律變化. 文中描述了一種數字的全面的頻率穩定度測量方法,該方法結合了數字雙混頻時差和數字邊沿效應的特點,使用低速、低分辨率的模/數轉換器實現高精度的測量,并且隨著所用模/數轉換器分辨率的提高,測量精度也會有一定的提高.經過實驗證明,這種方法測得的瞬態穩定度能夠達到 10-5/100 ns ,短期穩定度能夠達到 10-12/s,長期穩定度能夠達到10-16/d. 參考文獻: [1] 白麗娜, 周渭, 惠新明, 等. 頻率標準瞬態穩定度的精密測量[J]. 西安電子科技大學學報, 2014, 41(2): 102-106. BAI Lina, ZHOU Wei, HUI Xinming, et al. Precise Measurement of the Transient Stability of Frequency Standards[J]. Journal of Xidian University, 2014, 41(2): 102-106. [2] ZANETTE D H. Frequency Stabilization by Synchronization of Duffing Oscillators[J]. Europhysics Letters, 2016, 2(115): 20009. [3] 偶曉娟, 周渭, 易韋韋, 等. 精密頻率測量邊沿效應的特性分析[J]. 西安電子科技大學學報, 2016, 43(3): 144-148. OU Xiaojuan, ZHOU Wei, YI Weiwei1, et al. Characteristic Analysis of the Border Effect in Precision Frequency Measurement[J]. Journal of Xidian University, 2016, 43(3): 144-148. [4] PROCHAZKA I, PANEK P, KODETJ. Precise Phase and Frequency Comparator Based on Direct Phase-time Measurements[J]. Review of Scientific Instruments, 2014, 85(12): 126110. [5] BRIDA G. High Resolution Frequency Stability Measurement System[J]. Review of Scientific Instruments, 2002, 73(5): 2171. [6] BAI L N, SU X, ZHOU W, et al. On Precise Phase Difference Measurement Approach Using Border Stability of Detection Resolution[J]. Review of Scientific Instruments, 2015, 86(1): 015106. [7] 王正明, 董紹武, 劉春俠, 等. NTSC的雙混頻時差測量系統試運轉結果分析[J]. 時間頻率學報, 2006, 29(2): 134-141. WANG Zhengming, DONG Shaowu, LIU Chunxia, et al. Test Running and Data Analysis on the Dual Mixer Time Difference System at NTSC[J]. Journal of Time and Frequeney, 2006, 29(2):134-141. [8] 趙科佳, 張愛敏, 徐清華, 等. 數字式雙混頻時差測量系統的試驗研究[J]. 儀器儀表學報, 2014, 35(12): 2858-2865. ZHAO Kejia, ZHANG Aimin, XU Qinghua, et al. Experimental Research on Digital DMTD Measurement System[J]. Chinese Journal of Scientific Instrument, 2014, 35(12): 2858-2865. [9] 周翠. 基于FPGA的高斯濾波器的快速實現[J]. 空軍雷達學院學報, 2011, 2(3): 186-188. ZHOU Cui. Fast Implementation of Gaussian Filter with FPGAs[J]. Journal of Air Force Radar Academy, 2011, 2(3): 186-188. Methodofacomprehensiveresponsetimeoffrequencystability XULongfei,LUODan,ZHOUWei,BAILina,LIZhiqi,MIAOMiao (School of Mechano-electronic Engineering, Xidian Univ., Xi’an 710071, China) To reveal the change of the frequency stability of a different frequency source with the response time in essence, a method of measuring the comprehensive response time of frequency stability is proposed. In the digital environment, the digital edge effect is used to inhibit the quantization error, combined with the digital double mixing time difference method to measure the phase difference between the signals, by which the comprehensive frequency stability index is obtained. In experiments, the frequency source realizes the frequency stability of a more comprehensive change rule over time. Experiment proves that the method under the condition of self-calibration, transient frequency stability can be 10-5/100 ns, that short-term frequency stability can be 1012/s, and that frequency stability for a long time can be 1016a day. digital;quantization error;double mixing time difference;frequency stability 2017-03-04 時間:2017-06-29 國家自然科學基金資助項目(11773022);陜西省重大科技成果轉化引導專項資助項目(2015KTCG-01) 許龍飛(1990-),男,西安電子科技大學碩士研究生,E-mail: 18710849321@163.com. http://kns.cnki.net/kcms/detail/61.1076.TN.20170629.1734.026.html 10.3969/j.issn.1001-2400.2018.01.013 TM935.12 A 1001-2400(2018)01-0072-04 (編輯: 齊淑娟)3 頻率穩定度測量系統
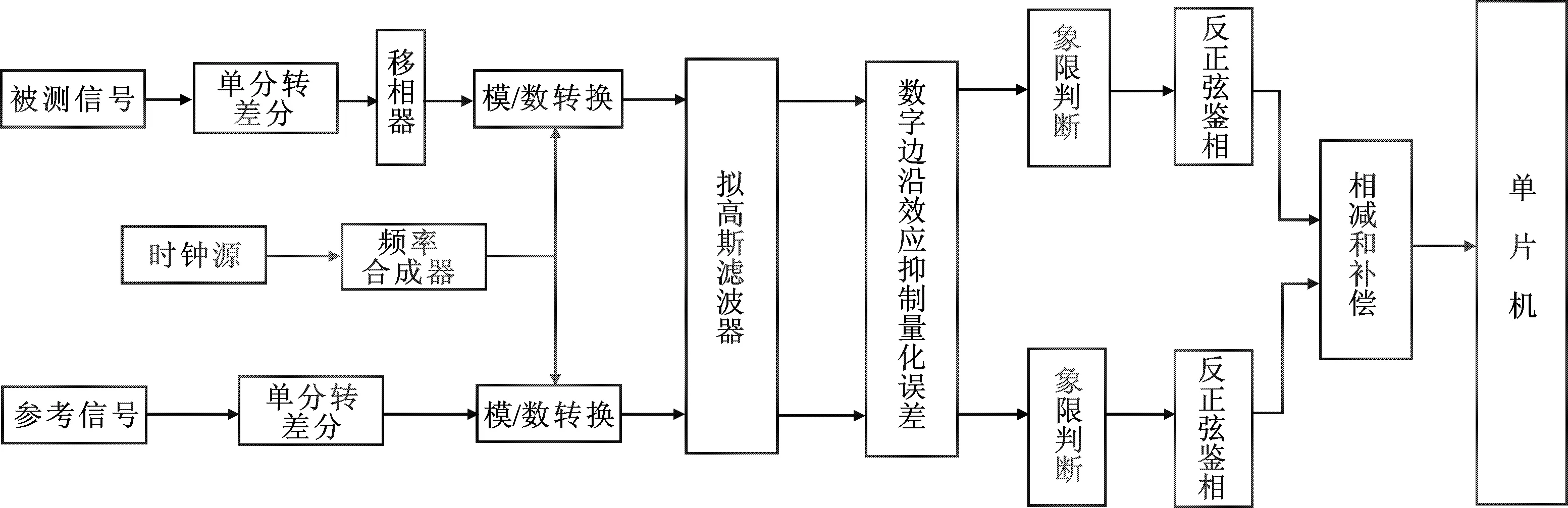
4 實驗論證和誤差分析

5 結 束 語

