函數多元問題的解法探究
張笑晗
(河北省辛集中學 052360)
題目已知函數f(x)=axlnx(a≠0),
(1)求函數f(x)的單調區間和最值;
(2)若m>0,n>0,a>0,證明:f(m)+f(n)≥f(m+n)-a(m+n)ln2.
分析本題是一道導數的練習題,數量關系看似簡單,實質上不盡然.第(1)問考查利用導數確定含參函數的單調性和最值,屬常規題型;第(2)問考查含有多個參變量的不等式的證明,初讀題目往往會感到無從下手或陷入繁瑣的運算之中.解題的關鍵有兩個轉化難點:一是參數a如何分類討論,二是三個參數m、n、a向哪個方向轉化.筆者從不同的角度去思考問題,探究多種解法.
解法探究(1)求函數f(x)的單調區間和最值

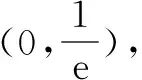
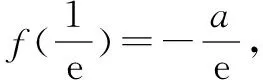

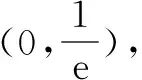
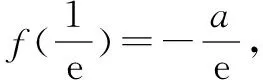
(2)若m>0,n>0,a>0.證明:f(m)+f(n)≥f(m+n)-a(m+n)ln2.
解法一:直接賦值構造函數
對于證明與函數有關的含多個參變量的不等式時,常常需要構造輔助函數,通過求導研究其單調性或尋求其幾何意義來解題.題目本身特點不同,所構造的函數可有多種形式,解題的繁簡程度也因此而不同.正確分析函數不等式的結構,恰當構造函數成為解題的突破口.
通過分析題目條件,發現涉及的三個函數f(m)、f(n)、f(m+n)中都含有參變量a,提取公因式結合a的取值范圍進而定號,只剩兩個參變量m和n,可以考慮將其中一個參變量賦值x,另一個看成常數,構造出新函數,問題就迎刃而解了.
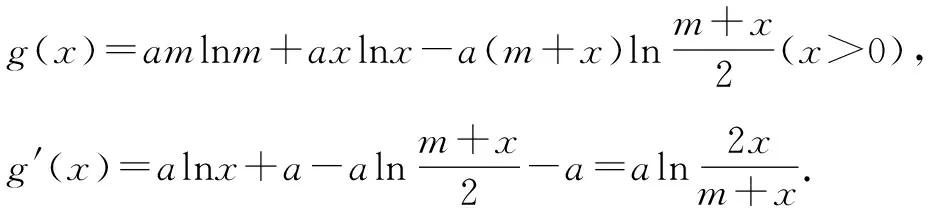
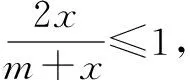
∴g′(x)≤0,g(x)單調遞減.
∵m≥x>0,∴g(x)≥g(m)=0,
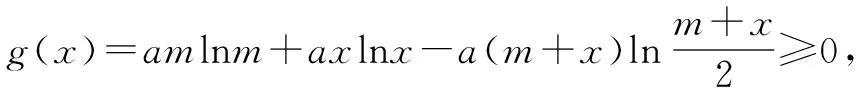
即f(m)+f(n)≥f(m+n)-a(m+n)ln2.
解法二:統一變量構造函數
在數學解題過程中,如果我們總是能嘗試以不同的視角分析并解決同一個問題,會幫助我們理解知識之間的關聯,對學習產生積極的作用.消元構造函數是解決含多變量函數的一種有效方法,通過消元這一方法的實施,求解問題的思路也就逐漸明朗起來,從而使問題得以順暢解決.實際上,我們可以通過確定兩個參變量m和n之間的比例關系,統一成一個變量代入求解,構造出新函數,討論也就有了方向.
不妨設m≥n>0,則m=kn(k≥1).
左邊-右邊=a[mlnm+nlnn+(m+n)ln2-(m+n)ln(m+n)]
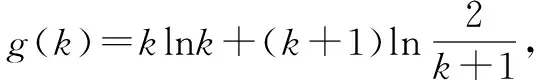
∴g(k)在k∈[1,+)上單調遞增,∴g(x)≥g(1)=0.
又∵n>0,a>0,∴左邊-右邊≥0,
即f(m)+f(n)≥f(m+n)-a(m+n)ln2.
解法三:借琴生不等式構造函數
琴生不等式(也稱為詹森不等式):
(1)設f(x)為凸函數,對于其定義域上的n個數x1,x2,…,xn,都有
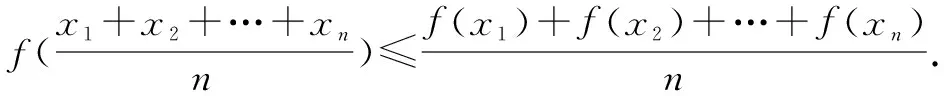
(2)設f(x)為凹函數,對于其定義域上的n個數x1,x2,…,xn,都有
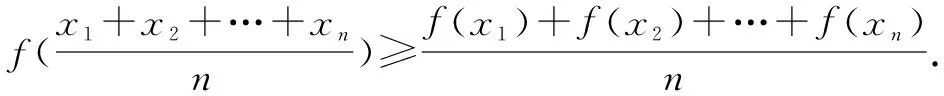
通常情況下用初等方法判斷函數的凹凸性比較麻煩,不過如果利用數學分析我們可以有個非常方便的結論:
如果f(x)二階可導,且f″(x)≥0,那么是下凸函數(凸函數);
如果f(x)二階可導,且f″(x)≤0,那么是上凸函數(凹函數).
有了這個結論以后,使用琴生不等式就非常方便了.解題關鍵是對不等式形式的結構特征有嚴格要求,識別是前提,轉化靠聯想.
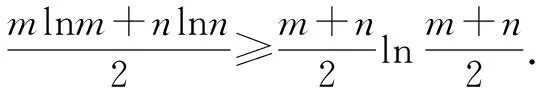
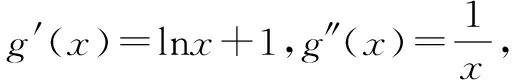
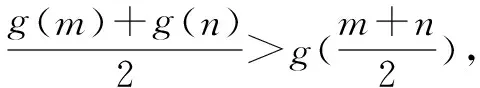
參考文獻:
[1]趙優良.例析多元參數的函數綜合問題解法[J].中學生數學,2017(03).

