關于高中物理動量問題的探究

肖 凱

(湖南省長沙市雅禮中學 410007)

一、動量與動量守恒定律

十七世紀初，意大利物理學家伽利略首先引入“動量”這個名詞.法國數學家笛卡兒繼承與發展了伽利略提出的動量概念.1644年，他在《哲學原理》中寫道：“當一部分物質以兩倍于另一部分物質的速度運動，而另一部分物質卻大于這部分物質兩倍時，我們應該認為這部分的物質具有相同的運動.”笛卡兒是把物質的多少和速度的乘積作為動量——物體“運動的量”的量度的.但由于那時“質量”的概念尚未建立，而且笛卡兒還未考慮到速度的方向性，因此動量的意義還未十分明確.

1687年，英國物理學家牛頓首次明確地定義了質量的概念，緊接著就定義了動量.他說：“運動的量是用它的速度和質量一起來量度的.”在這里，牛頓關于運動量度的思想是同笛卡兒、惠更斯等一致的，但因為建立了質量的概念和明確了速度的方向性，把動量作為一個矢量.因此，這是物理學的發展史上第一次真正建立了動量的概念.

動量可以按照以下公式計算：P=mv(1)

式中，P為物體的動量，其含義為：物體的動量等于物體質量與其速度的乘積.

高中物理的兩大守恒定律，其中之一就是與動量相關的動量守恒定律.在討論動量守恒定律之前，我們需要認識另一個物理量：沖量—I.沖量表述了對質點作用一段時間的積累效應的物理量，其表達式可以寫為：I=F·Δt.和動量是狀態量不同，沖量是一個過程量.

根據牛頓第二定律：F=ma(2)

等式兩邊同乘Δt，有F·Δt=m·a·Δt=mΔv=ΔP

上式的含義可以表述為：物體所受合外力的沖量等于它的動量的增量.這也就是我們常說的動量定理.

根據動量定理，我們很容易得出下列兩個結論：

1.“物體”如果不受到外力，那么這個“物體”的動量守恒.

2.動量與力具有方向性，所以動量守恒也具有方向性.

二、高中物理的碰撞問題

碰撞的定義：在極短時間內，至少2個物體相遇而使物體的運動狀態發生變化.

按軌跡分為正碰和斜碰，按動能是否損失分為彈性碰撞與非彈性碰撞.彈性碰撞遵循動能守恒與動量守恒定律；非彈性碰撞只遵循動量守恒定律，(非彈性碰撞包括完全非彈性碰撞).

無論是彈性碰撞還是非彈性碰撞，都遵循動量守恒定律.下面以簡單的碰撞模型來解釋碰撞過程中的動量守恒規律.

圖1

1.彈性碰撞

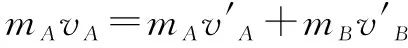
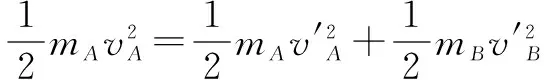
根據①②,解得

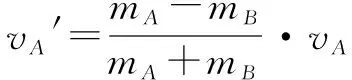
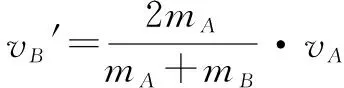
由③④兩個等式分析以下幾種特殊情況：a)若mA=mB則有vA′=0，vB′=vA，兩物體速度交換；b)若mA?mB則vA′≈-vA，vB′=0，A物體以方向相反的相等速度撞回；c)若mA?mB時，vA′≈vA，vB′=2vA,A物體速度基本不變，而B的速度以2vA飛出.

2.對心碰撞與非對心碰撞

中學階段主要研究對心碰撞，即碰撞之前的兩物體速度在同一直線上，碰撞后速度仍會沿著這條直線，也叫正碰.對于非對心碰撞，可以將動量分解，以向量的形式表現，根據同一方向上的動量守恒規律，列式求解.

三、例題分析

1.彈性碰撞模型

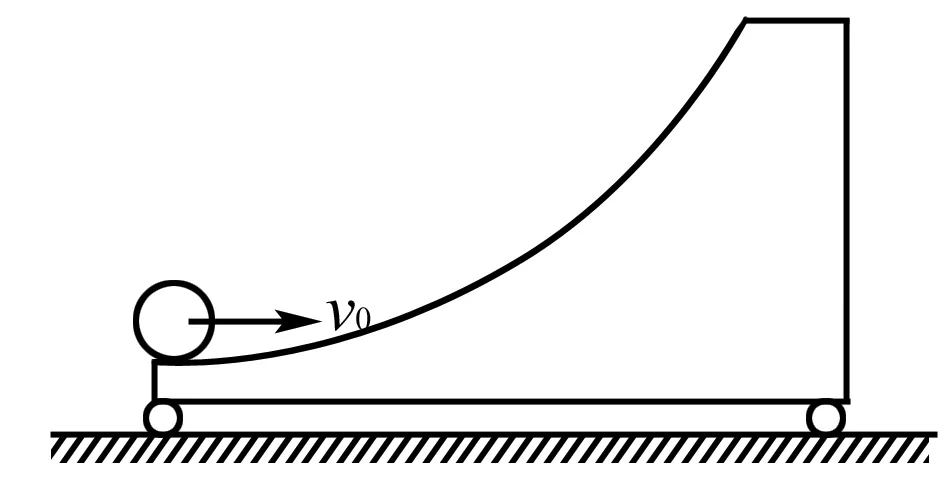
圖2

解析初看這道題，若從力這一方面去解題，似乎是不可能的，是一個曲面受力情況不清楚.所以我們應從能量角度來分析，抓住臨界狀態.

一開始，小球m會在曲面上不斷“爬升”，因兩物體的相互作用，小車開始加速，某一時刻，小球達到最高點，兩者達到共速，然后小球m向下滑，因相互作用，小車仍會加速，直到小球回到出發點.

最高點時：能量守恒，有

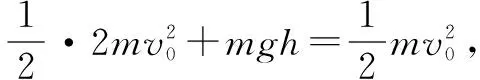
將之看成一個質量為m的小球去“碰撞”另一個質量為m靜止的小球，沒有能量損耗，即能量守恒，所以這是一個“彈性碰撞”，根據前面的結論，速度為v0的小球去碰撞另一個等質量且靜止的小球，交換速度，所以很容易得出正確答案B、C.

2.非彈性碰撞模型

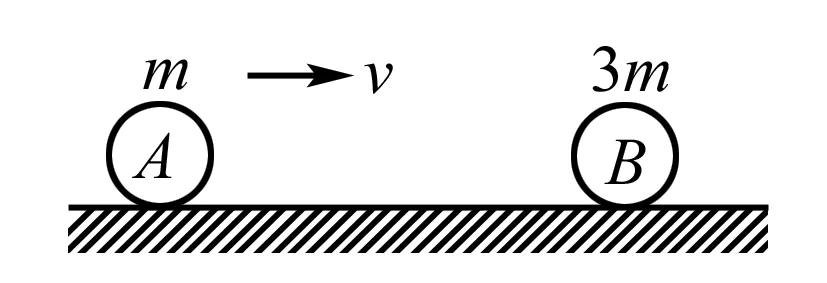
圖3

例2 如圖3所示：質量為m，速度為v的A球與質量為3m,靜止的B球發生正碰，碰撞可能是彈性，也可能是非彈性的，因此碰撞后的B球速度允許有不同的值，請你論證：碰撞后B球的速度可能是( ).

A.0.6 m/s B.0.4 m/s C.0.2 m/s D.0.1 m/s

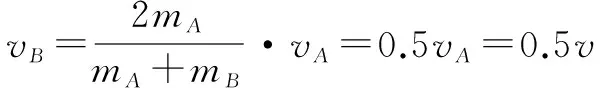
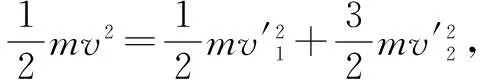
3.微觀世界中的動量

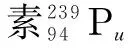
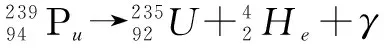
已知質量虧損Δm=mpu-(mu+mα)，則E=Δmc2，設E0為釋放出的能量，全部轉化為動能.

設Eu與Eα為鈾核動能與α粒子的動能.

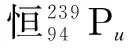
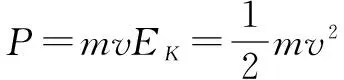
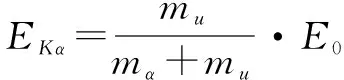
參考文獻：

[1]滿建真，黃國華，李越.高中生物理成績的影響因素及相關對策[J].亞太教育，2016(17):143.

[2]曹煒航.應用于高中物理“圖象法”解題中的圖象斜率探析[J].中國新通信，2017(01):136.

[3]王亦揚.分析高中物理實驗的學習對策[J].科技資訊，2017(01):139.