高中數學解題中應用分類討論思想之實踐
梁世杰
(山東省實驗中學 251401)
一、高中數學解題中應用分類討論思想的重要性
當前,分類討論思想是指將問題中多個已知條件相關的集合歸結成若干個子集,從子集內部入手逐一分析問題的局部解,隨后將多個局部解組合起來,由此得知原問題答案的一種思想方法.我們在應用分類討論思想解決數學問題時,在劃分條件過程中需要選定一個標準,做到不要重復不要遺漏任何要素,這也是分類討論思想的關鍵所在.其一,基于分類討論思想的指導,我們的解題思路將變得更為清晰,邏輯更合理.但是因為數學知識過于抽象,在解題過程中我們依舊會感到十分吃力.通過不斷強化數學思維,靈活把握分類討論思想,能夠增強問題解答能力.其二,在應用分類討論思想過程中,能夠幫助我們更加準確把握問題本質,將多個復雜的數學條件化整為零,從而準確解答問題.
二、應用分類討論思想需要注意的問題
在應用分類討論思想解決數學問題時,我們需要尤其注意以下幾個方面的問題:其一,在進行分類討論過程中要保證標準的統一性,在層次分明的情況下,保證分類不重不漏;其二,在分類討論期間,依據題目設定的條件準確判定討論的程度,在確定好討論對象及具體標準后,準確對應各個類別信息,保證不要出現漏掉的情況.在此基礎上進行歸類合并.需要注意的是,級別與級別間有著十分嚴格的排列要求,類別則沒有順序要求.其三,在整合過程中需要明確是先取交集再取并集,還是兩者皆不取只是逐一列出.
三、高中數學解題中分類討論思想的具體應用
1.數學概念、公式方面的應用
概念作為思維的引線,高中數學教材中多個概念都具備獨有內涵,在解答數學問題過程中,若是涉及到數學概念的問題,我們可以利用其概念對其進行分類討論.在討論過程中需要多加留心概念的受限條件.
例1 設圓錐曲線r的兩個焦點分別為F1,F2,若曲線r上存在點P滿足|PF1|∶|F1F2|∶|PF2|=4∶3∶2,則曲線r的離心率等于( ).
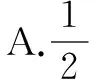
解析圓錐曲線并沒有給定時,因此我們需要實現討論是哪一類圓錐曲線,否則將很有可能出現漏解,鑒于本題中所給曲線有兩個焦點,因此我們不需要考慮拋物線.
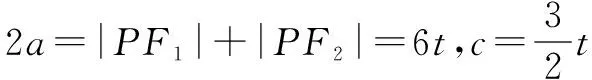
2.函數方面
在應用分類討論思想解決高中數學函數問題時,我們需要事先了解參數的意義,對參數的不同取值或者取值范圍進行分類討論,保證分類的合理性.我們在解題過程中需要注重技巧的累積,針對問題多個對象進行分類討論,從而全面把握解題要素,不斷提升問題解答準確率.
例2 (2016高考全國卷甲)已知函數f(x)=(x+1)lnx-a(x-1).
(1)當a=4時,求曲線y=f(x)在(1,f(1))處的切線方程;
(2)若當x∈(1,+∞)時,f(x)>0,求a的取值范圍.
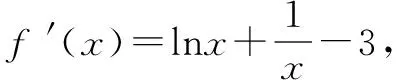
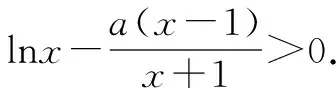
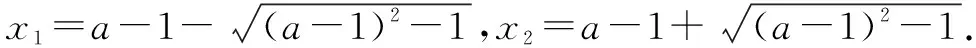
綜上所述,a的取值范圍(-∞,2].
3.概率方面
高中數學教材中概率統計知識應用十分廣泛,也是歷年高考數學測試中必考的內容.在解答此類問題時,我們需要巧妙利用分類討論思想,深度剖析問題本質,依據數學問題提出的多項要求進行合理分類,從而準確求解其問題.其一,我們需要事先確定問題的具體類型;其二,對現有多個解題條件進行排序,使用分類討論思想對相關變量進行設定;其三,借助準確的分類討論,求得正確的結果,不僅能夠節省許多時間,且能夠有效訓練我們的數學思維.
4.數列方面
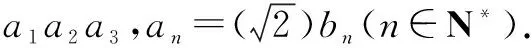
綜上所述,高中數學解題中應用分類討論思想,能夠有效激發我們的數學思維.在日常學習活動中,我們需要不斷擴大分類討論思想的應用范圍,總結方法的使用技巧,注重錯題累積,從而不斷提升我們的學習成績.
參考文獻:
[1]方驍.高中數學解題教學中分類討論思想的培養[J].文理導航(中旬),2017(02):5-6.
[2]孫志權.分類討論思想在高中數學解題中的應用研究[J].數學大世界(中旬),2017(06):79.
[3]沈淼楠.分類討論思想在高中數學解題中的應用[J].課程教育研究,2017(12):146-147.

