初中生對無理數概念理解的調查與研究
張 碩,張雪妮,2
(1.河北師范大學 數學與信息科學學院 050024; 2.河北省撫寧第二中學 066300)
一、問題的提出
我國《全日制義務教育數學課程標準(2011年版)》指出:了解無理數與實數的概念并能用有理數估計一個無理數的大致范圍.我國香港地區中學數學課程標準指出:體驗有理數與無理數,發展利用數來構想及解決問題的各種策略.美國中學數學課程標準中指出:在初中階段安排學生學習有理數,無理數,實數等知識.英國中學數學課程標準指出:中學生需要理解并使用實數中的有理數與無理數并能確定區間邊界.日本中學數學課程標準中指出:在數的有關概念的教學中要重視數的意義及大小,并通過數軸來表示數來說明數之間的大小.荷蘭中學數學課程標準指出:學生需學會估算,包括與小數和分數有關的估算,并能對估算結果的準確性做出判斷,而且可以將分數轉化為小數.通過以上各國中學數學課程標準對無理數的提出,可看出無理數在世界各國中學數學中都占有很重要的位置.
但是,據筆者對中學老師的一些訪談及側面對學生的了解,發現許多學生認為無理數比有理數難懂,對無理數的相關概念,性質等學得一塌糊涂,有些學生甚至不知道無理數是什么,對于有理數的區別也模模糊糊.許多教師認為無理數比較抽象,雖是初中數學的難點,但因中考所占比例不大,因此對這塊內容不夠重視,也不作更深講解.筆者還發現一部分教師對無理數發展史也不清楚,雖然教材把無理數編制了一整節內容,但還是不能引起學生及教師的關注.因此筆者認為有必要對學生無理數知識的學習情況進行調查研究.
二、研究過程
2.研究對象
筆者選取了河北省石家莊市的幾所不同層次學校的部分九年級學生進行了預調查,并通過整理分析,最終選取河北省石家莊市第二十二中這所普通中學的九年級不同層次的四個班級132名學生作為本研究的測試樣本,其中重點班學生共為61人,普通班學生共為71人.
3.研究工具
本文研究使用的測驗工具為預測卷、正式測試卷、訪談提綱.
3.統計方法
本研究實際回收試卷132 份,實際有效卷為127份.試卷中所有試題均為主觀題目,且均不記分,對問題結果進行水平劃分或對學生回答情況進行歸類統計.為了根據學生的回答比較學生對無理數概念的掌握情況,筆者借鑒了比格斯的SOLO分類系統將學生對第一題和第二題進行水平的編碼劃分,具體劃分標準說明如下:
水平1:相當于SOLO分類系統的前結構水平.
這一結構水平的學生的回答基本上無法理解無理數的本質特征.
水平2:相當于SOLO分類系統的單一結構水平.
這一結構水平的學生在回答無理數的定義時只找到了無理數的某一類型或者只提及到無理數概念的某一個側面或舉例說明就此結束回答.
水平3:相當于SOLO分類系統的多元結構水平.
這一結構水平的學生在回答無理數的定義時找到了可以代表無理數的多種不同的表現形式,但卻未能把這些不同形式有機嚴謹地整合在一起.
水平4:相當于SOLO分類系統的關聯結構水平.
這一結構水平的學生在回答無理數定義時找到了多個無理數概念的表現形式或者知識點,并且能夠把這些知識點串聯起來.
水平5:相當于SOLO分類系統的抽象拓展結構水平.
這一結構水平的學生回答無理數定義時能夠將無理數的概念進行多種不同表述的抽象概括,并且表述邏輯嚴密,思路清晰,涵蓋了所有的知識點.
三、研究結果及分析
問卷中的第一題是讓學生寫出自己所理解的無理數的概念,并要求學生盡可能多的寫出不同的表達方式,第二題是讓學生從眾多數中選出無理數,目的是要考察學生是否真正掌握了無理數概念的本質.答卷中學生的回答呈現出不同的水平,筆者借鑒了SOLO分類系統進行水平劃分(具體劃分標準見研究過程中的統計方法),表1反映了學生對無理數概念的回答水平分布情況.
表1學生對無理數概念的回答水平分類統計表
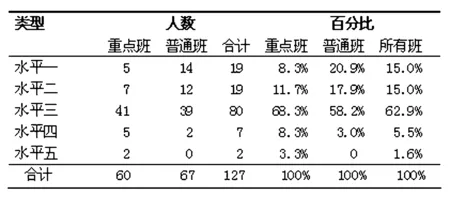
從上表數據可以看出學生對無理數概念的回答情況絕大部分處于水平3(多元結構水平)共有80人,占全部被試人數的62.9%;處于水平1(前結構水平)、水平2(單一結構水平)、水平4 (關聯結構水平)的學生人數相對較少,所占被試人數的比例分別為15.0%,15.0%,5.5%;而處于水平5(抽象結構水平)的學生水平人數更是寥寥無幾,僅占所有被試人數的1.6%.其中重點班的學生對無理數概念的掌握情況相對普通班學生對無理數概念的掌握情況要好一些,但差距不是很大.
筆者在統計中發現很多學生出現了同樣的幾種典型錯誤并做了如下整理:
典型錯誤一:不知道π、e也是無理數.
典型錯誤五:認為無理數只包含小數中的無限不循環小數、開方開不盡的數、以及用特殊符號表示的π、e中的其中一種或兩種.
為了更加了解學生發生錯誤的原因,筆者對個別學生進行了采訪,下面為一段訪談記錄(T表示筆者,S1表示學生1,S2表示學生2),由于有些學生表達不是很清楚,因此對一些回答筆者做了一定的邏輯整理.
T:你認為無理數包括哪幾種表現形式?
S1:帶根號的、除不盡的兩個數的商、無法開出來的平方根.
S2:開方開不盡的、帶π的數、無限不循環的小數.
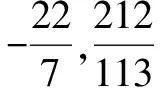
S1:他們都除不盡,應該是無理數.
S2:他們是分數應該是有理數,但他們又除不盡好像又是無限不循環小數是無理數,這樣的話不太清楚.
由以上問卷測試和訪談結果可發現絕大多數學生對無理數概念的把握處于不完全理解的狀態,他們大多數表現為能夠正確地表達出無理數的定義,卻對無理數的幾種表現形式不清楚,沒有掌握無理數的本質.還有些同學不明白分數除不盡的小數是無限循環的并不屬于無理數,因此在題二中選擇無理數時出現各種各樣的錯誤.
五、教學建議
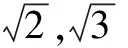
參考文獻:
[1]中華人民共和國教育部.全日制義務教育數學課程標準(修訂稿)[M].北京:北京師范大學出版社,2011.
[2]楊秀娟.初中生對無理數概念的理解[D].上海:華東師范大學,2007:1.

