垂徑定理牽手勾股定理
謝 勇 唐雪鋒
(湖北省棗陽市興隆一中 441218)
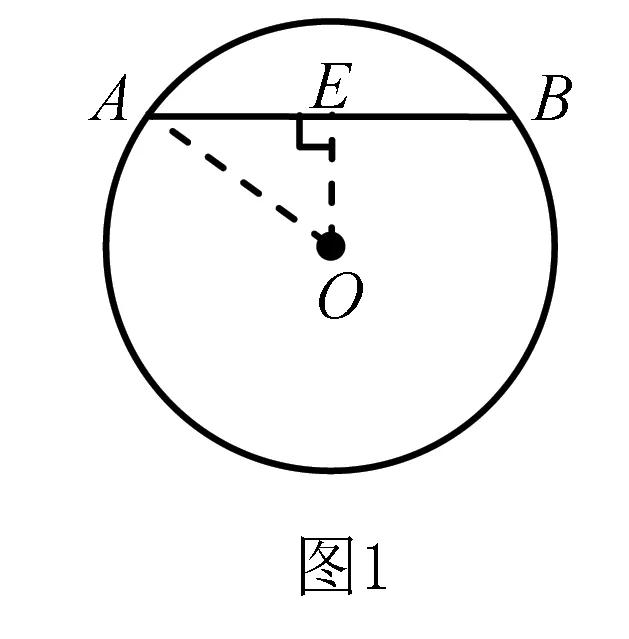
典例(人教版數學教材九年級上冊第83頁練習第1題)如圖1,在⊙O中,弦AB的長為8 cm,圓心O到AB的距離為3 cm.求⊙O的半徑.
解過點O作OE⊥AB,E為垂足,連接OA.
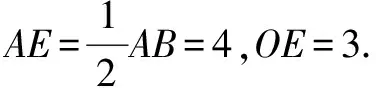
在Rt△AEO中,∵OE2+AE2=OA2,
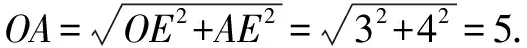
∴⊙O的半徑為5 cm.
規律解題過程中涉及垂徑定理和勾股定理.在圖1中,OA是半徑,我們把OE叫做弦心距(即圓心到弦的距離),AE叫做半弦,求解與垂徑定理相關的圓類計算問題時,通常需要把相關數量集中到由它們所組成的直角三角形中,運用勾股定理解決.
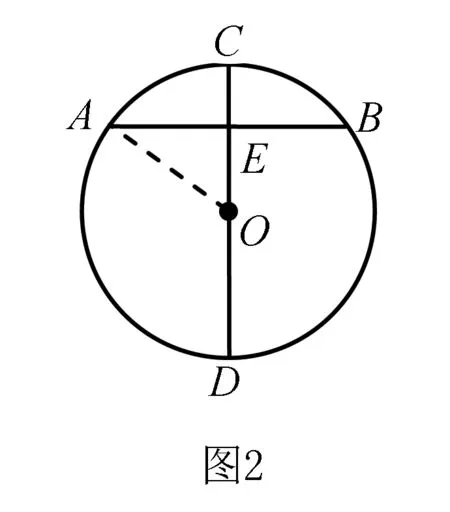
思考1 將條件與結論互換位置思考.如圖2,⊙O的半徑為5 cm,CD為直徑,弦AB⊥CD于點E,OE=3 cm,求弦AB的長.
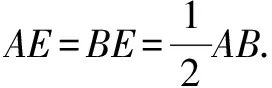
點評典例是已知半弦、弦心距,求圓的半徑問題,而本題是已知半徑、弦心距,求半弦的問題.探究幾何問題的一種常用方法就是象這樣,將已知條件與結論互換位置思考.另外,比較圖1和圖2,發現在解決有關弦的問題時,往往只需從圓心作一條與弦垂直的線段即可.
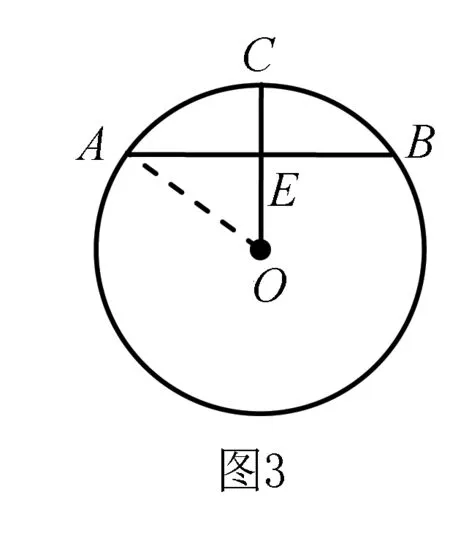
思考2 變換條件思考.如圖3,在⊙O中,弦AB的長為8 cm,點C在⊙O上,且OC⊥AB,垂足為點E,若CE=2 cm,求⊙O的半徑.
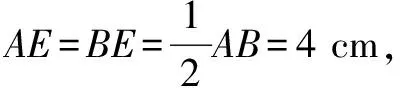
點評和典例相比,它們均是在同一個直角三角形中運用勾股定理計算求解.所不同的是,本題構建的是弦長、半徑、弦心距等數量間的方程模型,這和課本第82頁的例題解法是一樣的.
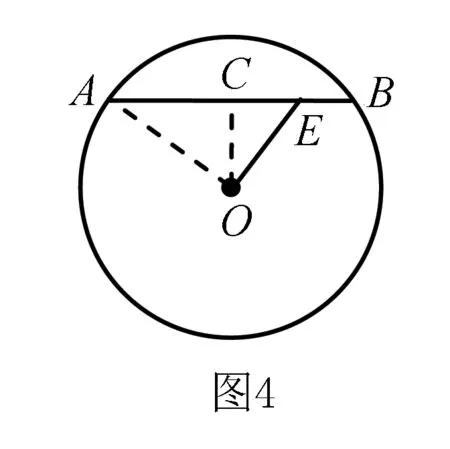
思考3 將靜止圖形動態化思考.如圖4,⊙O的直徑為10 cm,弦AB的長為8 cm,E是弦AB上的一個動點,那么OE的長的取值范圍是____.
分析求OE的長的取值范圍,實際上就是找OE的最大值和最小值,弦上的點與圓心的距離的最大值就是該圓的半徑,而最小值是弦心距.
點評動態化思考圖形,可多取幾個點E,并將它與圓心連接起來,比較后,會發現其中蘊含著垂線段最短的數學道理.
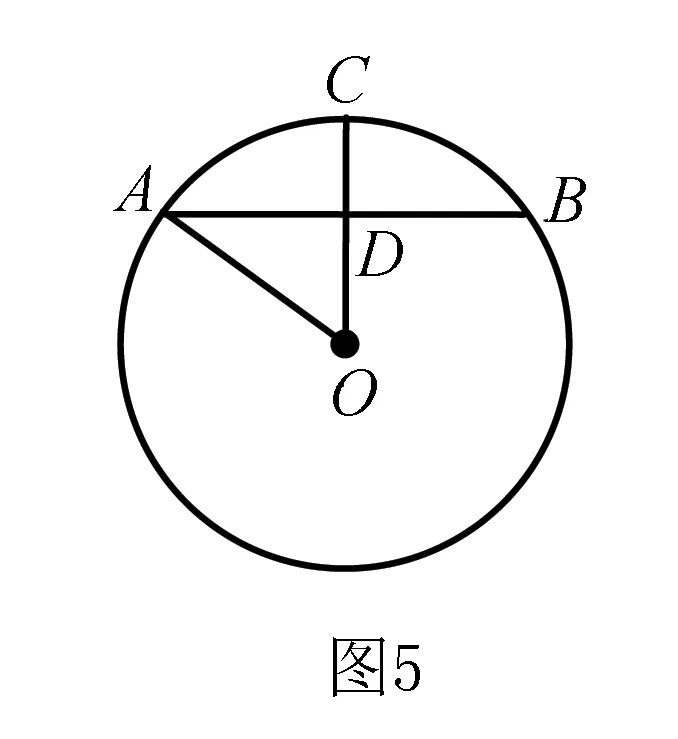
小結如圖5,在⊙O中,OC⊥AB于點D,AB=l,OA=R,OD=d,CD=h,根據OA2=AD2+OD2及OC=OD+CD,當知道l、R、d、h中的任意兩個量時,就可以求出剩余的兩個量.
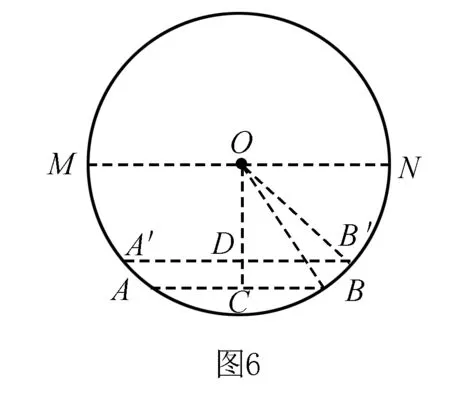
拓廣探索如圖6,在圓柱形油槽內裝有一些油,截面如圖,油面寬AB為6分米,如果再注入一些油后,油面AB上升1分米,油面寬變為8分米,圓柱形油槽直徑MN為____分米.
解取油面AB上升1分米到達A′B′的位置,過點O作OC⊥AB于點C,交A′B′于點D,連接OB,OB′.
∴AB=6,A′B′=8,CD=1.
由勾股定理,得OB2=OC2+CB2,OB′2=OD2+DB′2.
而OB=OB′,OC=OD+CD=OD+1,
∴(OD+1)2+32=OD2+42,解得OD=3.
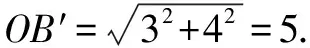
∴MN=2OB′=10(分米).
故答案填10.
點評這是一道與圓有關的實際應用題,求解關鍵是從中構建如典例1那樣的基本圖形,綜合運用垂徑定理和勾股定理構建方程求解.
參考文獻:
[1]姜曉翔.基于“自主變式” 引發“生本探究”[J].中國數學教育(初中版),2016(10):15-17.

