學科能力生根的學習過程優化
——試卷評講前引導學生問題的探究
季 揚
(江蘇省泰興市第一高級中學 225400)
《國家中長期教育改革和發展規劃綱要》把“提高質量”作為教育改革和發展的核心任務,提高教育質量,就是要“堅持育人為本、德育為先、能力為重、全面發展”.如何在綜合實踐活動課程和學科教學中落實“提高質量”和“四個堅持”目標的要求呢(這已是擺在我們每一位教育工作者面前的不可回避的重要課題)?其中,堅持“能力為重”就是要以發展學生的能力為重點,在實踐活動中發展學生的學習能力、實踐能力和創新能力,注重培養廠大中小學生的終身發展必備的基本能力;堅持“全面發展”就是要在社會實踐中感悟個人發展與社會發展息息相關.
一、教學活動中的案例
老師在試卷講評課后,都會精選一些題目給學生進行有針對性的訓練,使課堂上的知識點和解題方法能得以鞏固和落實.我認為在試卷講評課之前,結合試卷中的一些題目,適當地設計一些具有探究性的問題,要求學生通過自己的整理和研究,觀察和發現,先行一次拓展.同時,為第二天的講評能更加貼近學生的實際做好充分的準備,這也是提高試卷講評有效性的一種好策略.本文,結合自己在一次高三試卷講評課之前布置的作業題,談談幾種可行的問題設計形式.
設計一列表整理試題分布、分值及得分情況
問題1 根據試卷題型和得分分布,完善表格

試題類型題號分值得分情況復數運算函數的性質三角運算 ……
設計意圖:讓學生在數據統計中發現自己在哪些題型上的失分較多,對知識點的把握不到位,可以更好地查漏補缺.教師也能有的放矢地對試卷上錯誤較多的問題加以講解,避免一講到底的現象,或是重復學生會的,而對不會的卻沒有充分重視.
設計二尋求一題多解
已知圓C:(x-1)2+(y-2)2=2,點P坐標為(2,-1),過點P作圓C的切線,切點為A,B,求切點弦方程.
問題2 你能嘗試用多種解法處理此題嗎?
該題是解答題中的第二小問,學生在解決的時候會找不到切入口,若是評講前讓學生先從之前的試卷中對比尋找,或是和同學共同探討,就會發現該問題的解決方法不止一種,再加以整理對比,尋求最佳解題方法.現對學生整理的反饋如下:
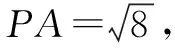
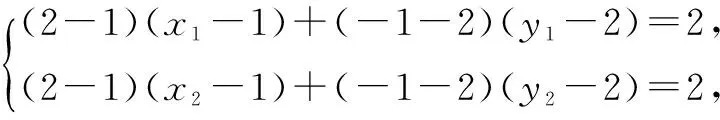
可見點A、點B的坐標都滿足x-3y+3=0,
所以直線AB為x-3y+3=0.
設計意圖:學生在找不到方法的時候,會覺得能解決問題的都是好方法,殊不知有些題目的思維方式獨特,通過探究合作,可以拓展學生思維,培養學生解決問題的能力,老師也能避免出現閉門造車的現象發生,有時候學生的方法比老師的方法更簡便,讓師生共同收益.
設計三探究錯題正解
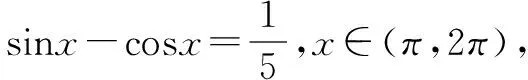
這道簡單的填空題,學生錯得比較多.讓學生自己根據錯解找出問題所在.
問題3 這樣解對嗎?錯在哪兒呢?怎樣改正?
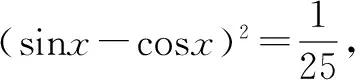
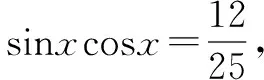
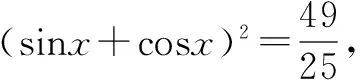
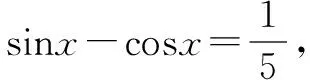
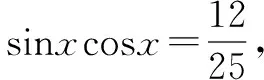
設計目的:學生自己先對錯解進行分析,弄清了錯在何處,然后找出正確的解答.這個過程其實就是學生再學習、再認識、再提高的過程,它使學生對易出錯的知識理解更全面透徹,掌握更加牢固,同時也提高了學生自主學習的能力.
設計四一題多變拓展知識點
已知函數f(x)=x3+ax2+x+b(a,b∈R)在x∈R上是單調函數,則實數a的取值范圍是 .
問題4 你能否在不改變函數f(x)解析式的前提下,給出此題一些合理的變式題?
考題是試卷中的一道填空題,利用此題設計了問題4.學生通過比較和聯系平時做過的一些題目,給出的變式題還是相當不錯的.整理部分如下:
變式①:已知函數f(x)=x3+ax2+x+b(a,b∈R)在x∈R上不是單調函數,則實數a的取值范圍是 .
變式②:已知函數f(x)=x3+ax2+x+b(a,b∈R)在x∈(0,1)上是單調增函數,則實數a的取值范圍是 .
變式③:已知函數f(x)=x3+ax2+x+b(a,b∈R)有三個單調區間,則實數a的取值范圍是 .
變式④:函數f(x)=x3+ax2+x+b(a,b∈R)有極值的充要條件是 .
設計意圖:學生在對原題進行變式的過程中會加深對題目已知條件的分析,進一步理解知識點之間的聯系,在變化的過程中體會數學的奇妙與藝術,對學習數學產生更加濃厚的興趣.
設計五通過對比歸納解決同類問題的方法
問題5 怎樣通過此題歸納出求不等式恒成立中參數的取值范圍的方法?
學生通過過歸類大致有這樣三種方式:①圖象法;②求最值法;③分離參數法.
函數f(x)=3mx2-6(m+1)x+6>0(m<0)在x∈[-1,1]上恒成立,求m的取值范圍.
1°-1≤m<0時,f(1)>0.
2°m<-1時,f(-1)>0.
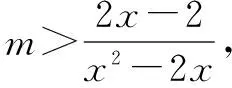
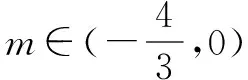
設計意圖:學生通過整理,對解決含參數問題的題型加以對比和總結,就能得到解決這類問題的一般方法,這對學生構建知識體系有很大的幫助.
設計六多題同種方法解決
問題6 下面三道都是不同的題目,但也都是求參數的取值范圍,你覺得最適合他們的同一方法是什么呢?
題①:函數f(x)=kx-lnx在(1,+)單調增,則k的取值范圍是____.
題②:方程x3-3x-a=0有三個不等的實根,求a的取值范圍.
題③:不等式x2-mx+1>0在x∈[1,2]上恒成立,則m的取值范圍是____.
三道題表面看似毫無關聯,但是他們都是含參數的問題,所以分離參數法是比較合適的方法.
我們可以在分離參數后構造新函數,進行求解.
設計意圖:分析貌似毫無關聯的幾題,尋找可用同一方法解題的特征.能讓學生在考試中減少思考時間提高解題效率.
試卷評講的最終目的是讓學生糾正錯誤,避免再次出錯.在評講試卷之前根據試卷大題情況,設置一些引導性的探究性問題,以作業的方式呈現出來,讓學生真正體現自主探究和合作學習的實質,也能通過比較找出自己在學習中的優點與不足,培養學習的興趣與習慣.也極大地提高了教師評講試卷的效率.
參考文獻:
[1]劉長貴.培養學生數學思維能力的幾種途徑[J].湖南教育,2002(5).

