具樁靴自升式鉆井船插樁過程有限元模擬研究

安永寧

(1.交通運輸部天津水運工程科學研究所，天津 300456；2.天津市水運工程測繪技術重點實驗室，天津 300456)

自升式鉆井船在海洋石油領域用途廣泛，多用于鉆井、修井，有時也被改造后用于采油作業中。自升式鉆井船依靠3～4根樁腿插入海底面以下一定深度的持力層，獲得承載力支撐上部荷載[1]。目前，許多自升式鉆井船都在樁腿端部裝有樁靴裝置，樁靴一般為紡錘形或錐形，截面呈正多邊形或圓形，截面最大尺寸在6～12 m范圍。

樁靴的應用，提高了自升式鉆井船插樁就位時的作業效率，增強了其在深厚軟土海區的適用性，基礎的自穩性也得到進一步增強。另外，較淺的插樁深度，一方面充分利用了淺部承載力，另一方面使得拔樁不再困難，易用性和安全性都顯著提高。

新結構的應用需要相應理論方法的更新完善。在評價具樁靴自升式鉆井船的插樁深度時，工程技術人員對于插樁作業中地基土的破壞機理、荷載影響深度等的認識并不明晰，在承載力計算時，有時將樁靴視作淺基礎考慮，有時又視作樁基礎考慮，這種疑惑甚至在具樁靴自升式鉆井船的使用手冊中都有反映[2-3]。

本文基于基礎的極限破壞理論，應用有限元數值模擬手段，研究了具樁靴自升式鉆井船插樁作用于均質地基土時，地基土的破壞模式和插樁荷載影響深度，以及不同承載力計算公式的適用性，解決了具樁靴自升式鉆井船在實際應用中的工程技術疑難。

1 自升式鉆井船承載力計算現狀

目前，對具樁靴自升式鉆井船的地基承載力及插樁深度進行評價時，常見的方法有兩種，一種是以Skempton公式[4]、Terzaghi公式[5]、SNAME[6]規范等推薦的淺基礎計算方法，另一種是以API RP2A[7]等規范推薦的樁基礎承載力計算方法。

1.1 均質土淺基礎承載力計算方法

(1)均質砂土。Terzaghi在假定條形基礎且基礎底面粗糙、地基處于整體剪切破壞、滑動范圍內土體處于塑性平衡情況下，根據彈性楔形體的平衡條件得出了極限承載力計算公式

Pu=0.5γBNγ+γDNq+cNc

(1)

通常樁靴貫入地層屬于圓形或方形基礎作用，此時，若地基土發生局部剪切破壞，太沙基建議的相應修正公式如下

Pu=0.3γBNγ+γDNq+0.8cNc

(2)

以上公式中，c為地基土的黏聚力，γ為地基土的有效重度，B、D分別為基礎的寬度(直徑)和埋深，Nγ、Nq、Nc均為與內摩擦角相關的承載力系數，可查表求得。

(2)均質飽和軟黏土。Skempton研究了飽和軟黏土地基的極限承載力計算，解決了Terzaghi公式在φ=0條件下難以應用的問題

(3)

式中：Cu為基礎底面以下0.707B深度范圍內的地基土不排水抗剪強度；L為基礎的長度，對于大部分樁靴，L=B；承載力系數Nc取5.14。

以上公式是基于均質地基土、破壞面已知、條形基礎埋深固定不變等假定條件下，依據靜力學平衡關系建立起來的，而海上自升式鉆井船的樁靴基礎一般為圓形或方形，地基土成層且非均質，插樁過程是不斷貫入和破壞地基土的動態連續過程，很難滿足公式的假定使用條件，因此，從理論上來說，將其用于計算樁靴承載力時不夠精確。

1.2 SNAME規范樁靴承載力計算方法

美國造船與輪機工程師學會(the Society of Naval Architects & Marine Engineers, SNAME)發布的RecommendedPracticeforSiteSpecificAssessmentofMobileJack-upUnits中，給出了具樁靴鉆井船插樁承載力的計算公式。

(1)在不排水飽和黏土中，不考慮回淤影響時，地基土可承擔的樁靴極限豎向荷載按下式計算

(4)

式中：形狀系數sc=1+(Nq/Nc)(B/L)，對于飽和黏土，通常Nq=1、Nc=5.14；深度修正系數dc=1+0.4(D/B)；A為樁靴最大橫截面積；p0′為上覆的最大有效壓力。

(2)在硅質砂或其他粒狀土中，不考慮回淤影響時，地基土可承擔的樁靴極限豎向荷載按下式計算

(5)

式中：γ′為地基土的水下有效重度；形狀系數sγ=1-0.4(B/L)，sq=1+(B/L)tanφ；深度修正系數dγ=1，dq=1+2tanφ(1-sinφ)2f，當D/B≤1時，f=D/B，否則f=arctan(D/B)。

(3)在上軟下硬層狀土中，上層黏土會發生擠壓，不考慮回淤影響時，地基土可承擔的樁靴極限豎向荷載按Meyerhof給出的公式計算

FV=[(5+0.33B/T+1.2D/B)Cu+p0′]A

(6)

式中：T為軟土層中樁靴最大截面至下伏硬土層的厚度。

(4)在上硬下軟層狀土中，樁靴可能會發生沖切，當上部硬土層為硬黏土時，如不考慮回淤影響，地基土可承擔的樁靴極限豎向荷載按Brown給出的公式計算

(7)

式中：H為硬土層中樁靴最大截面至下伏軟土層的厚度；Cu,t為上部硬土層的不排水抗剪強度，Cu,b為下部軟土層的不排水抗剪強度。

當上部硬土層為砂土時，如不考慮回淤影響，地基土可承擔的樁靴極限豎向荷載按下式計算

(8)

式中：FV,b為假定插樁在下伏軟土層頂面且無回淤時的極限豎向荷載；Ks為沖剪系數，Kstanφ=3Cu/Bγ′。

SNAME方法在計算成層土的承載力時，假定樁靴預先插入一定的土層，沒有考慮插樁過程對土層分布的影響以及不同的破壞機制，當上覆砂土層下伏軟黏土層時，沒有考慮到上覆砂土層的強度性質，只給出了下限解，因而得到的結果也不夠精確[8]。

1.3 API樁基礎承載力計算方法

美國石油學會(American Petroleum Institute, API)發布的Planning,DesigningandConstructingFixedOffshorePlatforms-WorkingStressDesign(API RP2A-WSD)中，給出了海上樁基礎的單樁極限承載力計算方法，主要由極限樁端阻力和極限側摩阻力兩部分組成，在黏土和非黏土有著不同的計算方法。

(1)在不排水黏土中時，單樁極限承載力按下式計算。

Qd=Qf+Qp=fAs+qAp=αCuAs+9CuAp

(9)

(2)在非黏土中，單樁極限承載力按下式計算。

(10)

以上式中，f為單位樁側阻力，As為樁側總面積，q為單位樁端阻力，Ap為樁端總面積；α為不大于1的系數；Cu為計算點的不排水抗剪強度；K為橫向壓力系數，一般取1.0；δ為土與樁壁之間的摩擦角，Nq為與δ有關的支撐系數。

以上公式在計算無樁靴樁基礎時，適用性較好。但當具樁靴鉆井船插樁時，樁靴巨大的擴底效應完全擾動了樁側地層，導致插樁產生的側摩阻力很小，此外樁靴本身排出了相當大體積的土體，失去的這部分土體自重應增加到最終承載力計算結果中。因此，將API RP2A-WSD規范公式進行如下修正，更符合具樁靴鉆井船插樁的力學作用原理

Qd=Qp+γV

(11)

上式也是一部分自升式鉆井船操作手冊中給出的推薦計算方法，其中V是樁靴排開土的體積。

API方法推薦的公式屬于樁基礎公式，但具樁靴的自升式鉆井船插樁深度往往在5 m以內，或插樁深度小于樁靴尺寸，更符合淺基礎的判斷條件，API公式的應用效果如何尚需實際檢驗。

2 有限元數值模型建立

有限元法是一種求解偏微分方程邊值問題近似解的數值技術。巖土材料有著非線性、各向異性等力學性質，大多數巖土問題非常復雜，通常難以得到準確解，而有限元法計算精度高，能適應復雜形狀，在處理巖土工程問題中有著明顯的優勢[9-10]，一些學者利用有限元技術模擬了海洋工程插樁活動，取得了新的認識和符合實際的結果[11-19]。

本文擬采用有限元法，建立樁靴結構與海洋土體相互作用的有限元數值模型，對插樁活動進行數值模擬，通過將模擬結果與公式計算結果、插樁實例結果對比，來揭示具樁靴平臺插樁時的地基土破壞方式，以及不同條件下的承載力計算方法。

2.1 單元及本構模型

樁靴單元為完全積分的線性實體單元，材料選用各向同性彈性材料，材料參數包括密度、彈性模量、泊松比。

土體單元為完全積分的線性實體含孔隙流體單元，材料選用各向同性彈塑性材料，其中，不排水黏土的本構模型為Mohr-Coulomb模型，材料參數包括密度、彈性模量、泊松比、內摩擦角(Friction angle)、剪脹角(Dilation angle)、黏聚力(Cohesion yield stress)、塑性應變(Abs plastic strain)、偏心率(Deviatoric/Meridional eccentricity)；排水無黏土的本構模型為修正的Drucker-Prager/Cap模型，材料參數包括密度、彈性模量、泊松比、p-t平面黏聚力(Material cohesion)、p-t平面摩擦角(Angle of friction)、帽子偏心率(Cap eccentricity)、初始屈服面位置(Initial yield surface position)、過渡面半徑(Transition surface radius)、流動應力比(Flowstress ratio)，在帽子區域采用相關流動法則，在剪切破壞和過渡區域采用非相關流動法則。

Mohr-Coulomb模型屈服面函數為

F=Rmcq-ptanφ-c=0

(12)

(13)

cos(3θ)=r3/q3

(14)

以上式中，φ為材料內摩擦角，c為黏聚力，Rmc(θ,φ)為控制屈服面形狀的函數，θ為極偏角，r為第三偏應力不變量。

Drucker-Prager模型屈服面函數為

F=t-ptanβ-d=0

(15)

(16)

以上式中，β為屈服面在p-t應力空間上的傾角，與φ有關，k為三軸拉伸強度與三軸壓縮強度之比，d為屈服面在p-t應力空間t軸上的截距。

2.2 接觸關系

樁土之間的接觸關系為具有主從關系的面對面接觸，以樁的接觸面作為主面，土體接觸面作為從面，采用罰函數算法(Penalty algorithms)，垂向接觸屬性為“硬”接觸(Hard contact)，切向接觸可有限滑移(Finite sliding)，滑移摩擦由Coulomb接觸法則控制，樁土間的Coulomb摩擦系數為0.6。

2.3 荷載及邊界條件

整體模型受到的外部荷載主要為重力和靜水壓力，初始條件主要有重力、孔隙比和孔隙水壓力的分布，邊界條件包括側邊界的水平位移約束(U1=0)、底邊界的垂直位移約束(U2=0)、樁靴體的初始平動和轉動約束。為了控制整體模型在樁靴貫入之前不發生較大變形，首先設定地應力平衡分析步(Geostatic step)，在考慮樁土質量、形狀尺寸和整體受力情況下，使土體均勻沉降，達到地應力平衡狀態。樁靴的貫入采用位移貫入法，在土壤力學分析步(Soils step)中，通過指定樁靴體的豎向位移-時間(U2-t)函數來實現，貫入速率不宜太快，在黏土中小于0.1 m/s，在無黏土中小于0.05 m/s，且開始時以緩慢貫入過渡。由于插樁過程是荷載的快速加載過程，孔隙水壓力來不及消散，因此，采用瞬態(Transient)孔隙水壓響應方式。

2.4 應力平衡方程和滲流連續方程

土體應力平衡方程采用虛功原理來表示，在某一時刻土體的虛功與作用在該土體上作用力(體力和面力)產生的虛功相等

(17)

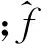
fω=(sn+nt)ρωg

(18)

在有限元法中，采用拉格朗日方程對該方程進行空間離散。

滲流連續方程是由同一時間內流入土體的水量等于土體的體積變化量這一連續條件來建立的

(19)

式中：vω為流體的平均流速；n是邊界S的外法線；ρω0為參考密度(Reference density)。

該連續方程采用反向歐拉近似法進行時間積分，孔隙水滲流服從Darcy定律或Forchhermer定律。Forchhermer定律的表達式為

(20)

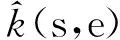
2.5 網格及模型尺寸

本文采用的樁靴整體類似于陀螺形，下部呈錐體，最大截面直徑為9.14 m。土體范圍總寬度為100 m，土體深度為40 m。樁靴周邊的網格單元尺寸為0.5 m，向遠處逐漸增大至5 m，以節省計算成本。整個模型共有節點738個，單元683個(圖1)。

2.6 模型驗證

圖1 土體及樁靴的有限元網格Fig.1 FEM meshes of spudcan and soil

對數值模型進行驗證，并修改和完善模型參數，可以提高模型的有效性和可信度。鑒于自升式鉆井船的插樁過程極其復雜，直接觀察其插樁阻力隨深度的變化情況，目前尚很難實現，而進行室內模型實驗不失為一種可行的驗證方案。目前業界完成的模型實驗并不多，本文以Craig和Chua完成的在離心機中模擬樁靴貫入黏土的試驗[20]來驗證數值模型，分別選取了不排水抗剪強度為39 kPa、63 kPa時的實驗結果進行驗證，由于是在黏土中進行實驗，且貫入深度較淺，因此，驗證時也加入了Skempton公式的計算結果，作為對比參考。

3 有限元數值結果分析

3.1 均質黏土中土體的破壞形式及承載力計算

2-a 39 kPa黏土中 2-b 63 kPa黏土中圖2 樁靴貫入數值模型的離心機實驗驗證曲線Fig.2 Verification curve between FEM and experiment results

在均質黏土中，對樁靴貫入10 m深度地層的插樁現象進行了有限元仿真模擬，采用的土體黏聚力從10～80 kPa范圍進行了試算，本文選取c=25 kPa時的模擬結果進行地基土的破壞形式、荷載影響深度及承載力計算方法的分析。c=25 kPa的黏土處于軟(soft)和中等(firm)狀態的界限，在中國渤海海域也較為常見，具有典型代表性。

(1)地基土破壞形式。插樁過程中的地基土破壞形式可用模擬結果中的等效塑性應變(PEEQ)來反應，圖3給出了插樁深度分別為1.0 m、2.8 m、4.0 m時的地基土PEEQ等值線分布。可以看出，當插樁至2.8 m之前時，樁靴底部存在貫通的塑性應變區，并延伸到海底面，此時地基易出現整體滑移，地基土的破壞形式類似于整體剪切破壞；當插樁深度在2.8～4.0 m范圍時，樁靴邊緣的地基土體塑性應變較大，但在樁靴底部并未貫通，地基土的破壞形式類似于局部剪切破壞；當插樁深度大于4.0 m時，地基土中不再形成延伸至海底面的塑性區，樁靴四周的土體發生沖切破壞，使樁靴連續刺入土中，極限平衡區限制在微小的局部范圍內，地基土的破壞形式類似于沖剪破壞。

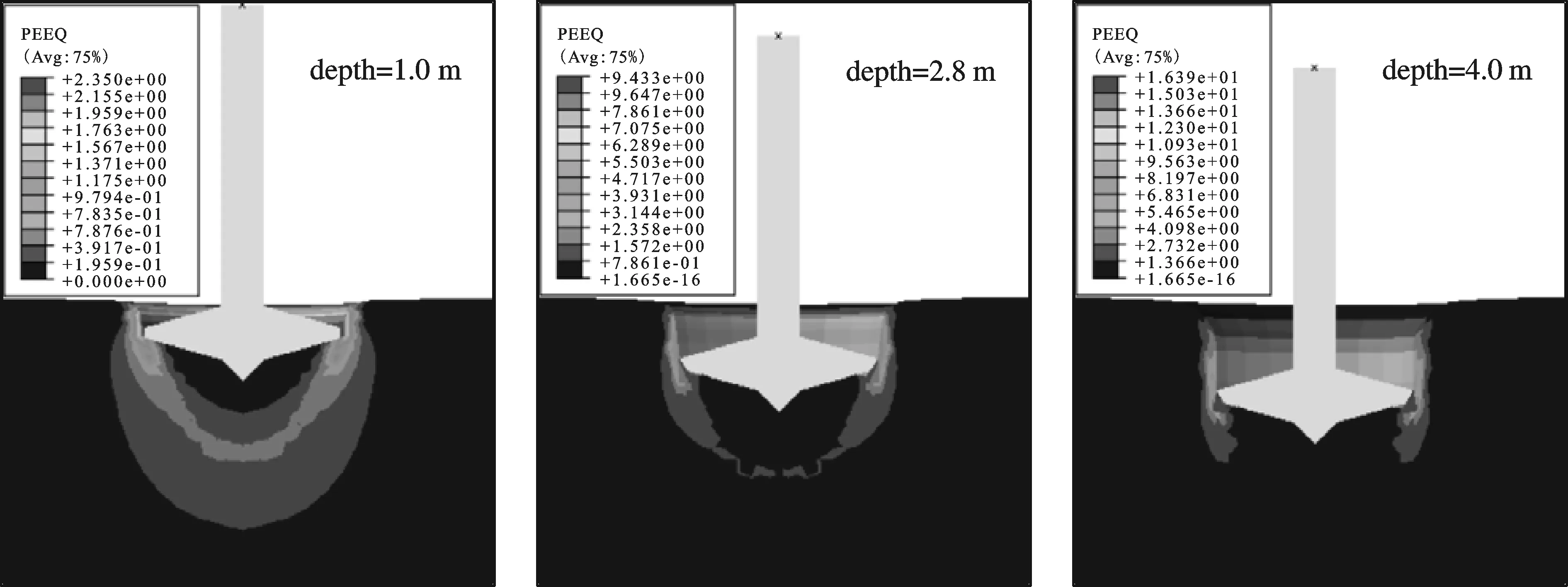
圖3 均質黏土中不同深度處等效塑性應變(PEEQ)分布圖Fig.3 PEEQ contour line in different depths in homogeneous clay

由此可見，當在黏土中插樁深度過小時，地基容易出現滑移，對自升式鉆井船的抗傾穩性不利，因此，在實際插樁時，除了承載力滿足條件，還要保證一定的插樁深度。

(2)插樁荷載影響深度。本文以地基土的受壓豎向位移(U2)和剪切應力(S12)的分布范圍來表示插樁荷載的影響深度。當插樁至1.5 m深度時，土體U2和S12的分布范圍開始與樁靴尺寸表現出較好的線性相關，當插樁至4.0 m以下深度時，即地基土的破壞形式類似于沖剪破壞時，U2和S12的分布范圍與樁靴尺寸的比例基本趨于固定，圖4給出了插樁深度為5 m時的U2與S12分布。土力學中有時將s/b=0.01所對應的荷載作為承載力特征值，本文在此以U2=0.01B作為插樁荷載影響深度的判別標準，模擬結果顯示，U2=0.09 m(0.01B)的土體分布范圍形似燈泡，其底界面距樁靴最大截面寬度處的垂向距離約為3.0倍基礎寬度，樁靴底部土體的剪切應力分布范圍似腎形，3.0B深度處的S12值約為10 kPa，為土體本構模型中黏聚力25 kPa的0.4倍。

圖4 均質黏土中土體豎向位移(U2)和剪切應力(S12)分布圖Fig.4 Distribution of U2 and S12 in depth of 5.0 m in homogeneous clay

(3)地基承載力計算。圖5給出了c=25 kPa時的有限元模擬地基承載力曲線及各公式計算結果，模擬曲線形態近似于a<1的冪函數，在淺部地層中曲率較大，隨著插樁深度的增大，其曲率逐漸趨小。

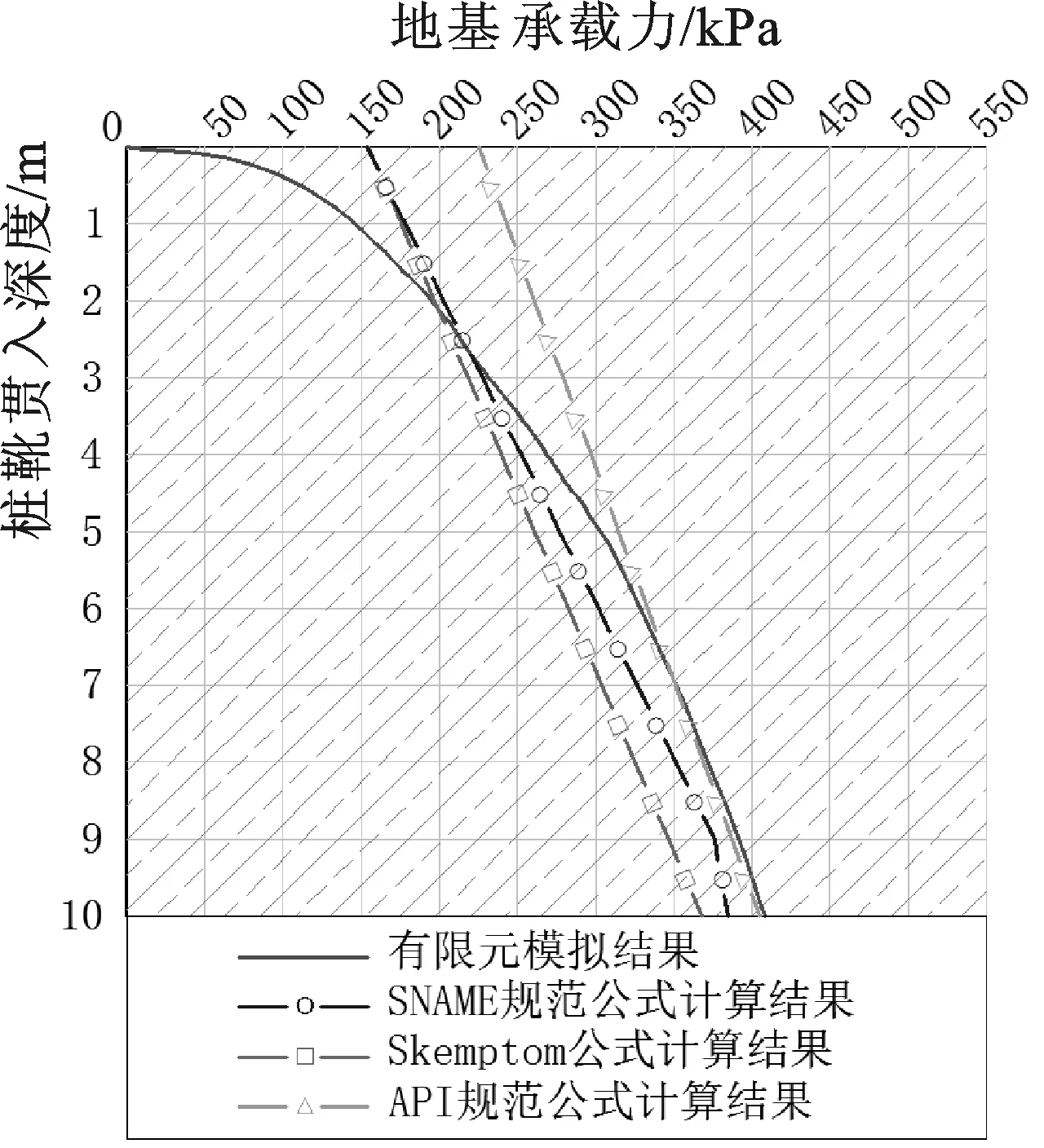
圖5 均質黏土中有限元模擬與公式計算結果對比(c=25 kPa) Fig.5 Comparison between FEM simulation and formulas calculation in homogeneous clay

有限元數值模擬結果與Skempton公式、SNAME規范公式的計算結果相交于2.2～2.5 m深度范圍，此后其走勢漸趨一致，而SNAME結果與數值模擬結果更為接近。在2.2～2.5 m以淺，公式計算結果較大，這是因為Skempton公式和SNAME規范公式都假定基礎已經埋置于特定深度、基礎側限存在邊載土壓力，而在數值模擬中，樁靴是自海底面開始貫入，貫入時并不存在邊載，而且，在貫入深度較淺時，樁靴底部的塑性應變區貫通，不利于兩側土體邊載土壓力的發揮，因此，其承載力開始貫入時幾乎為0，然后隨著邊載土壓力的逐步發揮，承載力呈曲線形逐漸增大。在2.2～2.5 m以下深度，公式計算結果的數值偏小，這主要是由于公式假定極限承載力為地基土發生塑性破壞時的承載力，而數值模擬的插樁過程不斷地破壞地基土，又不斷下適持力層，極限承載力發生在地基土發生了塑性破壞之后，再加上土體本構模型屬于彈塑性模型，因此模擬得出的數值更大。從樁靴貫入的形式來看，數值模擬的過程更接近實際插樁過程，在實際工程中，本文認為，Skempton公式和SNAME規范公式都可用于計算樁靴貫入均質黏土中的地基承載力，但在插樁深度過淺時(如2.5 m以淺深度)，公式的有效性會降低，本文建議忽略較淺部地層中的計算結果，將插樁深度設定在2.5 m以下深度，也有利于提高樁靴的抗滑移和抗傾穩性。

API RP2A規范推薦的計算公式屬于樁基礎公式，其計算結果與模擬結果的曲線相交于約6.9 m深度處，且其計算結果偏大，在實際工程中建議慎用。

3.2 均質砂土中土體的破壞形式及承載力計算

在均質砂土中，對樁靴貫入10 m深度地層的插樁現象進行了有限元仿真模擬，采用的土體內摩擦角從20～35°范圍進行了試算，本文選取φ=24°時的模擬結果進行地基土的破壞形式、荷載影響深度及承載力計算方法的分析。在中國渤海海域，淺層沉積的砂土多為稍密—中密狀態的粉砂或細砂，砂質粉土也較為常見，其土力學性質更接近粉砂，這些土的內摩擦角都較小。

(1)地基土破壞形式。圖6給出了插樁深度分別為4.0 m和10.0 m時的地基土PEEQ等值線分布。當插樁深度較淺時，樁靴底部存在貫通的塑性應變區，并延伸到海底面，地基土破壞形式類似于整體剪切破壞，這與prandtl在較硬地基土基礎淺埋情況的地基土破壞形式的認識一致[21]。當插樁至10.0 m以下深度時(略大于1倍樁靴直徑)，逐漸轉變為類似沖剪破壞。

(2)插樁荷載影響深度。圖7給出了插樁深度為5 m時的U2與S12分布，模擬結果顯示，U2=0.09 m(0.01B)的土體分布范圍形似燒杯，其底界面距樁靴最大截面寬度處的垂向距離約為3.0B，樁靴底部土體的剪切應力分布范圍似梨形，3.0B深度處的S12值約為30 kPa，為該深度處土體抗剪強度γ3.0Btanφ(97.6 kPa)的0.3倍。

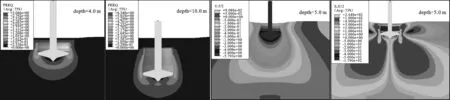
圖6 均質砂土中不同深度處等效塑性應變(PEEQ)分布圖Fig.6PEEQcontourlineindifferentdepthsinhomogeneoussand圖7 均質砂土中土體豎向位移(U2)和剪切應力(S12)分布圖Fig.7DistributionofU2andS12indepthof5.0minhomogeneoussand

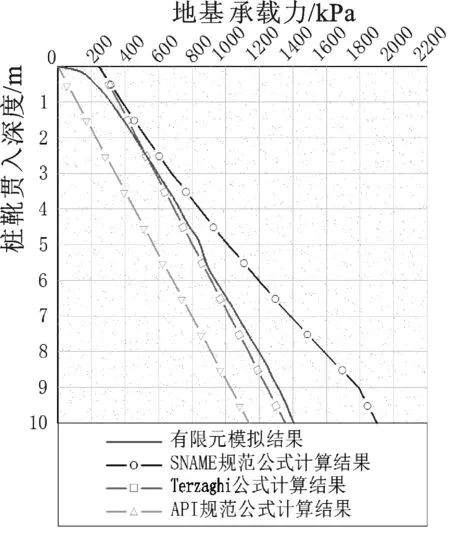
圖8 均質砂土中有限元模擬與公式計算結果對比(φ=24°)Fig.8 Comparison between FEM simulation and formulas calculation in homogeneous sand

(3)地基承載力計算。圖8給出了φ=24°時的有限元模擬地基承載力曲線及各公式計算結果，模擬曲線形態近似為直線，僅在1.0 m以淺為曲線。

有限元數值模擬結果與Terzaghi公式相交于約2.5 m深度處，此后無論是數值還是走勢都非常接近，這說明Terzaghi公式適宜于計算樁靴貫入均質砂土中的地基承載力，在2.5 m以淺，公式的計算結果偏大，仍是由于公式考慮了邊載土壓力的影響，而在數值模擬中，這是逐步產生和發揮作用的，因此，本文同樣建議在應用Terzaghi公式時，忽略較淺部地層中的計算結果。

SNAME公式的計算結果偏大，曲線走勢也與數值模擬結果不一致，這可能是由于該公式在第二項同時考慮了有效上覆壓力p0′和深度修正系數dq的影響，這2個參數都隨深度的增加而增大，本文不建議在均質砂土中應用該公式。順便一提，當不考慮dq的影響時，SNAME公式的計算結果與模擬結果更為接近，只是數值略大一點。

API RP2A規范公式屬于樁基礎公式，其計算結果盡管在曲線走勢上與數值模擬結果接近，但其數值偏小，本文不建議應用。

4 結語

通過以有限元數值方法模擬具樁靴自升式鉆井船貫入地層一定深度的動態過程，取得了地基土破壞形式、插樁荷載影響深度、地基承載力計算方法等多方面認識，按照地基土性質的不同，可分別總結為：

(1)在均質黏土中插樁時，隨著插樁深度的增大，地基土先后經歷了整體剪切破壞、局部剪切破壞、沖剪破壞3種破壞形式，插樁荷載的影響深度約為3.0B，Skempton公式和SNAME規范公式都適宜于計算均質黏土中樁靴荷載的承載力。

(2)在均質砂土中插樁時，地基土的破壞形式主要表現為整體剪切破壞，插樁荷載的影響深度約為3.0B，Terzaghi公式適宜于計算均質砂土中樁靴荷載的承載力。

(3)Skempton公式、SNAME規范公式(均質黏土中)、Terzaghi公式，都可用于計算樁靴貫入均質土時的地基承載力，但在插樁深度過淺時，受邊載土壓力未完全發揮等因素影響，公式的計算結果往往偏大，建議忽略較淺部地層中的計算結果，這也有利于提高樁靴的抗滑移性和抗傾穩性。

(4)將有限元數值模擬方法應用于海洋巖土工程仿真模擬，可適應復雜的工程邊界條件和地基土類型，在研究難以觀測的工程現象時極為方便，而在模型的建立與修繕方面無論是成本還是效率都遠甚物理試驗模型，因此具有無可替代的優勢。

參考文獻：

[1] 季春群, 孫春昌. 自升式鉆井船地基承載力抗傾穩性及樁腿插深分析[J]. 上海交通大學學報,1996, 30(3):79-85.

JI C Q,SUN C C. Analysis of Stability Against Overturning and Foundation Bear Force for Jack-Up Rig[J]. Journal of Shanghai Jiaotong University,1996, 30(3):79-85.

[2] 勝利石油管理局鉆井工藝研究院海洋所.中油海5鉆井平臺操作手冊[R].東營: 勝利石油管理局,2007.

[3]中國船舶工業集團公司第708研究所.中油海62平臺操作手冊[R].東營: 勝利石油管理局,2009.

[4]Skempton A W. The bearing capacity of clays[J]. Building Research Congress,London,1951,1:180-189.

[5] 錢家歡,殷宗澤.土工原理與計算:第二版[M].北京:中國水利水電出版社, 1996.

[6] SNAME. Guidelines for site specific assessment of mobile jack-up units[M]. New Jersey: Society of naval architects and marine engineers, Technical and Research bulletin5-5A,1997.

[7] American Petroleum Institute. Recommended practice for planning, designing and constructing fixed offshore platforms-working stress design (API RP2A-WSD)[M]. New York: American Petroleum Institute,2004.

[8] 殷齊麟,董勝,樊敦秋.復雜地層中自升式平臺插樁的數值模擬[J].工程力學, 2016, 33(9):204-210.

YIN Q L, DONG S, FAN D Q. Numerical Simulation of Penetration of Jack-up Platform in Complex Foundation Soils[J].Engineering Mechanics, 2016, 33(9):204-210.

[9] 王金昌, 陳頁開.ABAQUS在土木工程中的應用[M].杭州:浙江大學出版社,2006.

[10] 費康, 張建偉. ABAQUS在巖土工程中的應用[M].北京:國水利水電出版社, 2010.

[11] Hu Y, Randolph M F. A practical numerical approach for large deformation problems in soil [J]. International Journal for Numerical and Analytical Methods in Geomechanics, 1998, 22(5): 327-350.

[12]Mehryar Z, Hu Y. Penetration analysis of spudcan foundation in Ncclay [C]//Proceedings of the 12th International Offshore and Polar Engineering Conference.Kitakyushu, Japan, 2002:679-684.

[13] Erichson H L, Drescher A. Bearing capacity of circular footings [J]. ASCE, Journal of Geotechnical Engineering, 2002, 128(1): 38-43.

[14] Kellezi L, Stromann H. FEM analysis of jack-up spudcan penetration for multi-layered critical soil conditions [C]//Sarah M.Proceeding of BGA International Conference on Foundations.Dundee, Scotland, 2003:410-420.

[15] Kellezi L, Kudsk G. Spudcan Penetration FE Simulation of Punch-through for Sand over Clay [C] // Kellezi L.Proceeding of the 12th International Jack-up Conference.London, England, 2009:336-348.

[16] Kellezi L, Kudsk G. Spudcan Penetration FE Simulation of Punch-through for Sand over Clay [C]// Kellezi L. Proceeding of the 12th International Jack-up Conference.London, England, 2009:336-348.

[17] LIU J, HU Y X, KONG X J. Deep penetration of spudcan foundation into double layer soils[J]. China Ocean Engineering, 2005, 19(2): 309-324.

[18] Qiu Gang, Henke S, Jurgen Grabe. 3D FE analysis of the installation process of spudcan foundations [J]. Frontiers in offshore Geotechnics II, 2010:685-690.

[19] Qiu Gang, Jurgen Grabe. Numerical Simulation of the Deep Penetration Process of Spudcans into Sand Overlaying Clay Using the Extended Hypoplastic Models [C]//HUANG F J.Proceedings of the 22nd International Offshore and Polar Engineering Conference.Rhodes, Greece, 2012:681-688.

[20] Craig W H,Chua K. Deep Penetration of spudcan foundation in sand and clay[J]. Geotechnique, 1990,40(4): 541-556.

[21] 陳希哲. 土力學地基基礎[M]. 北京：清華大學出版社，2000.