基于一般二階混合矩的高斯分布估計算法

任志剛 梁永勝 張愛民 龐蓓

分布估計算法(Estimation of distribution algorithm,EDA)是一類典型的基于模型的進化算法.與基于交叉和變異等遺傳操作的其他進化算法相比,EDA具有較強的理論基礎,而且可以成功求解大量不同類型的連續和離散優化問題,近年來一直是進化計算領域的研究熱點[1?3].

本文重點研究面向連續問題的EDA,這類算法通常采用高斯概率模型(Gaussian probability model,GPM)描述優解的分布.根據對各變量之間相關關系的處理方式,高斯EDA(Gaussian EDA,GEDA)可以分為變量無關的EDA、部分變量相關的EDA、全變量相關的EDA,其代表性算法分別為PBILc(Population based incremental learning)[1]和UMDAc(Univariate marginal distribution algorithm)[1,4]、EGNA(Estimation of Gaussian networks algorithm)[4?5]、EMNAg(Estimation of multivariate normal density algorithm)[1].

GPM為EDA的理論分析提供了諸多方便,但同時也有一些不足,其中最顯著的一點是,直接由常用的極大似然估計(Maximum likelihood estimation,MLE)計算出的變量方差會快速減小,導致算法的探索能力急劇下降.已有研究通過保持各方差值至少為1[6]、將估計出的方差固定地放大一定倍數[7]、利用協方差矩陣(Covariance matrix,CM)的特征值修改方差[8]以及根據采樣解的改進情況自適應地調整方差[9?10]等策略來彌補這一不足.其中,Bosman等學者提出的自適應方差縮放策略影響最為廣泛[10].他們建議當算法在遠離均值的位置找到更優解時增大方差,而當算法在連續多次迭代內找不到更優解時減小方差.除方差快速減小這一不利因素之外,與CM相對應的概率密度橢球體(Probability density ellipsoid,PDE)的長軸還傾向于與目標函數的改進方向相垂直,這會大大降低GEDA的搜索效率[11?12].Cai等學者首次發現了這一現象,并將其與方差收縮問題合并處理,提出了基于概率分布交叉熵的自適應方差縮放策略[11].Bosman等學者則提出了預期均值偏移策略,該策略嘗試采用兩組分別以預估均值和偏移均值為中心的較優解來估計CM,從而改變PDE長軸的方向[12].將該策略與前期提出的自適應方差縮放策略相結合后,Bosman等學者構建了一種稱為AMaLGaM的有效EDA[13].

除上述研究之外,文獻[14?16]分別通過引入混沌變異算子、正則化技術、多群體–多模型方法來增強GPM 對不同問題的適應性;文獻[17?19]則放棄GPM,分別采用直方圖模型、粒子濾波、Copula函數來估計優解的概率分布;文獻[20]在直方圖模型的基礎上,進一步利用局部搜索技術提升EDA的優化性能;文獻[21]則嘗試采用有監督學習方法估計優解的條件概率分布,并借助Gibbs采樣技術提高搜索效率.這些研究工作在改進EDA性能的同時,也將算法模型復雜化,并引入了較多難以設置的自由參數.

本文在分析傳統GEDA性能弱化原因的基礎上,提出一種簡單高效的GEDA.該算法在每次迭代中首先根據選擇出的優秀樣本預估出一加權均值,然后顯式地利用預估均值的目標函數值將其偏移至一個更有希望的解區域中,最后根據所選優秀樣本關于偏移后均值的二階混合矩來估計CM.這一簡單操作可以在不增大算法計算量的前提下,自適應地調整PDE的位置、大小和長軸方向,使之盡可能與當前解區域的結構特征相契合,從而提高算法的搜索效率.根據CM 的計算方式,本文將所提算法命名為基于一般二階混合矩的高斯分布估計算法(General-second-order-mixed-moment based GEDA,GSM-GEDA).

1 基本分布估計算法

作為一種基于模型的進化算法,EDA假設待解決問題的優解服從某種概率分布,并利用根據當前群體中的較優解估計出的概率分布來產生下一代群體,從而驅動算法進化.基本EDA的步驟如下:

步驟1.設置算法參數,初始化群體.

步驟2.根據目標函數評價當前群體中各個解的質量.

步驟3.根據選擇規則選出優秀樣本集合.

步驟4.根據優秀樣本集估計概率分布模型.

步驟5.根據概率分布模型進行采樣,構建新群體.

步驟6.更新獲得的最優解并判斷是否滿足終止條件.若滿足,則輸出最優結果;否則,轉至步驟2.

連續型EDA通常采用GPM描述優解的分布.對于n維的隨機列向量x,GPM的聯合概率密度函數可以表示為

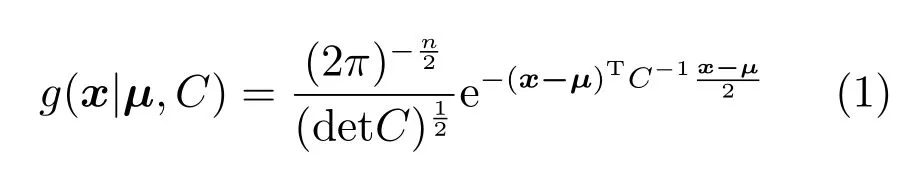
其中,μ和C分別表示x的均值和CM.在每次迭代中,GEDA通常根據截斷選擇規則選出優秀樣本集S,并采用MLE來估計μ和C:

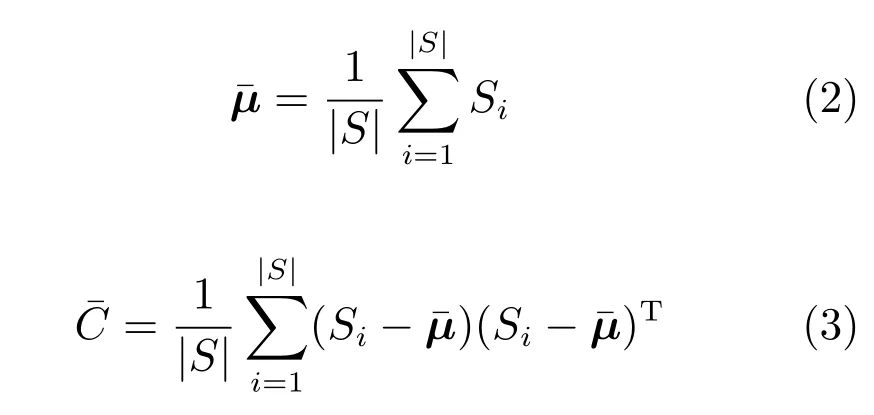
EMNAg算法采用式(1)～(3)所示的GPM及參數估計方法來綜合描述所有變量之間的相關關系.文獻[22]的研究表明,諸如EGNA等基于高斯圖的、部分變量相關的EDA可以納入到全變量相關的EDA框架之下.UMDAc和PBILc則通過忽略各變量間的相關關系,換取了具有較少參數的對角型CM.

上述三類GEDA針對各類型問題的求解性能雖有不同,但它們都采用MLE估計概率分布參數,由此具有兩個共性特點:1)各變量的方差會隨著算法迭代而快速減小[6,7,9?11];2)與CM 相對應的PDE的長軸傾向于與目標函數的改進方向相垂直[11?13].圖1給出了該現象的示意圖,造成該現象的主要原因是,GEDA在每次迭代中選出的優秀樣本主要分布在由目標函數等值線切割原PDE所形成的半橢球體內.該半橢球體的長軸平行于目標函數等值線;相應地,根據半橢球體內的優秀樣本以及MLE新估計出的PDE的長軸也平行于目標函數等值線,即傾向于與目標函數的改進方向相垂直.另一方面,該半橢球體內靠近原PDE中心的樣本較多,而遠離原PDE中心的樣本較少,那么根據這些樣本新估計出的PDE自然會發生收縮現象.傳統GEDA的這種特性大大降低了算法的搜索效率,導致算法即使在斜坡型解區域中也可能早熟收斂[9].

2 基于一般二階混合矩的高斯分布估計算法(GSM-GEDA)

在GEDA中,PDE的位置、大小和長軸方向分別決定了算法的搜索中心、范圍和主要搜索方向.我們期望PDE位于易于發現更優解的解區域中,其大小能夠根據當前解區域的結構特征自適應地變化,其長軸方向與目標函數的改進方向相一致.GSMGEDA通過修改均值和CM的估計方法來實現這一目的.

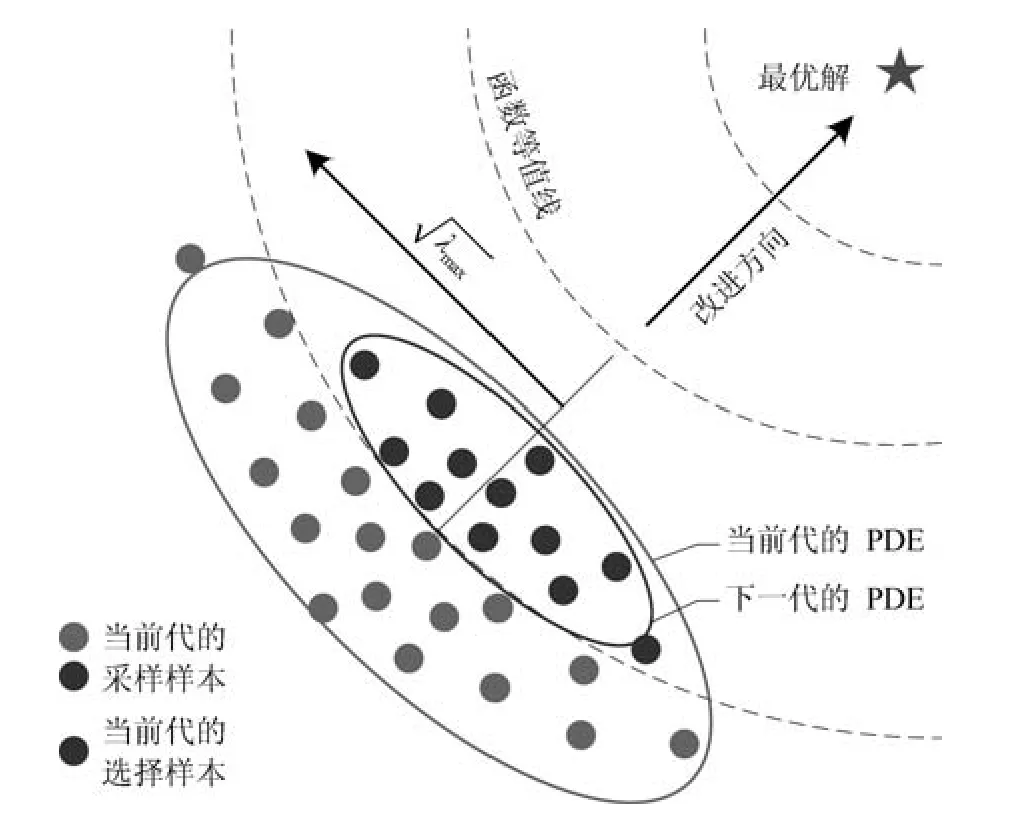
圖1 傳統GEDA中PDE的變化示意圖Fig.1 Schematic for the change of PDE of traditional GEDA

2.1 均值估計方法

在每次迭代中,為了盡可能獲得一個有前途的搜索中心,GSM-GEDA根據如下兩個步驟估計均值:

1)采用加權樣本預估均值.由式(2)估計出的均值實際上是優秀樣本的算術平均,如果對較優樣本賦予較大權重則有利于改進所估計均值的質量.具體地,GSM-GEDA首先根據下式為GPM預估出一均值:

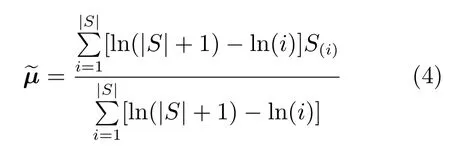
其中,S(i)表示集合S中第i個最優解.由式(4)可知,S(i)的權重與其排序的對數值成反比;排序越靠前,其權重越大.數值測試表明,在大多數情況下都優于.

2)沿目標函數的改進方向偏移預估均值.具體為:

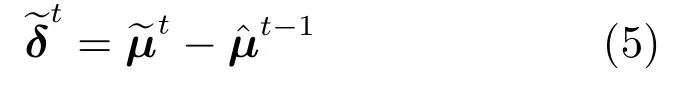
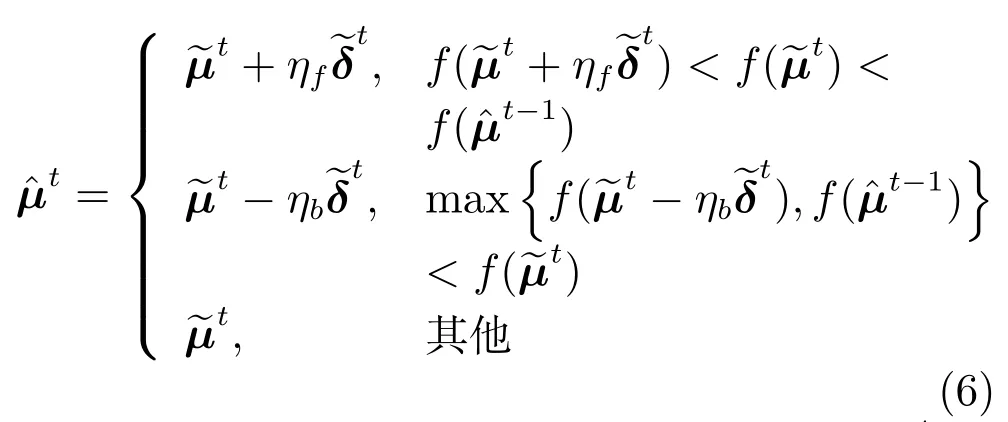
其中,t表示第t次迭代中偏移后的均值;表示當前預估均值t與上次迭代中偏移后均值之間的差異,它反映了算法的進化方向;f(·)表示需要極小化的目標函數.通過顯式地比較與可以獲得f(·)的一個改進方向.若優于式(6)嘗試沿的方向將偏移至其目的是發揮算法的搜索慣性,提高搜索效率,其中的ηf稱為前向偏移系數;最終能被接受的前提條件是相反地,若t差于式(6)則嘗試沿的反方向將偏移至其目的是及時修正算法的進化方向,使其與目標函數的改進方向相一致,其中ηb稱為反向偏移系數;也僅在優于的情況下才會被最終接受.當進行反向偏移時,一個合理的設置是允許最遠偏移至因此0＜ηb≤1;另一方面,大量測試表明,當ηf≥1時,可以前向偏移至一理想位置.綜合以上兩個因素,一般可以設置ηb=1/ηf.第2.2節將理論分析ηf對算法性能的影響;第3.1節將實驗測試ηf對算法最終求解質量的影響,并給出取值方案.

2.2 協方差矩陣估計方法

GEDA根據優秀樣本估計CM 的本質目的并不是準確獲得樣本自身的分布特征,而是希望利用這些樣本為下一次迭代確定一個合理的搜索范圍和方向.由第1節的分析可知,與式(3)所示估計相對應的PDE的大小和長軸方向是不理想的.另一方面,由概率論中關于矩的知識可知,隨機向量的CM 即為它的二階混合中心矩.那么在樣本不變的前提下,改變矩中心是調整PDE大小和長軸方向的一個簡單方法.對于GSM-GEDA來說,一個自然選擇是采用偏移后的均值代替式(3)中的MLE均值,即:

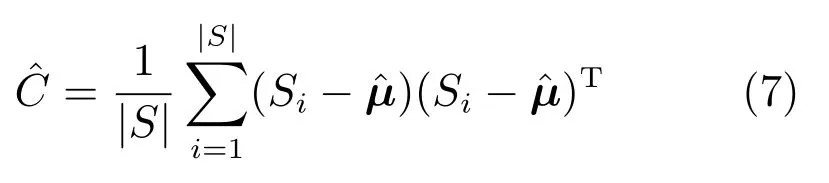
上式表示對以偏移后的均值這一一般位置為中心的二階混合矩的估計.

由式(5)和(6)可知,不差于;由式(4)可知,通常優于;相應地,一般會優于.那么,代表了目標函數的一個改進方向.與式(3)所示估計相比,式(7)給出的估計可以隨的改變而自適應地調整PDE的大小(體積),并且可以使PDE的長軸方向趨近于目標函數的改進方向().為此給出以下定理和推論:

定理1.對于選定的優秀樣本,若那么由所確定的PDE的體積不小于由確定的PDE的體積.

證明.由高斯分布的性質可知,PDE的各個軸的方向分別與CM的各特征向量相一致,而各半軸長度ad(d=1,2,···,n)由CM 的相應特征值λd確定:另一方面,由文獻[23]可知,PDE的體積與各半軸長度的乘積成正比.記的特征值分別為那么定理1成立的充要條件是,當為證明這一點,對做如下變化:

很明顯,矩陣的秩1修正[24].文獻[25]中的引理1.4對秩1修正后對角型矩陣的特征多項式進行了討論,根據該引理可以推得也即的特征多項式:

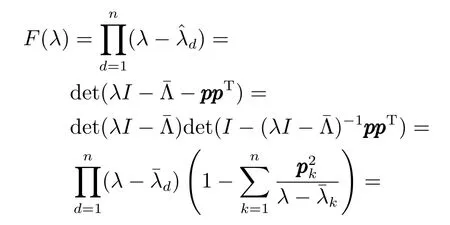
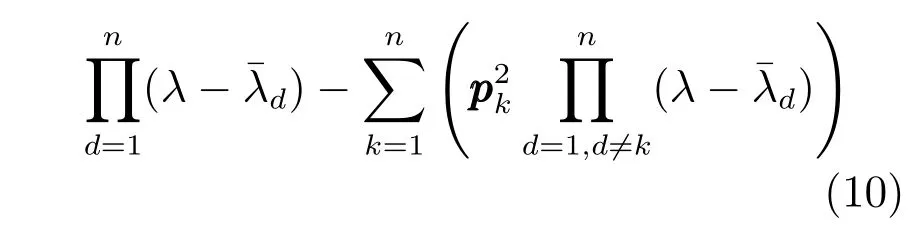
其中,I表示相應階數的單位陣.令式(10)中的λ=0,可得:

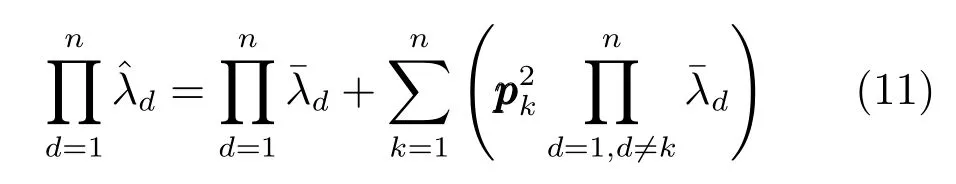
推論1.對于選定的優秀樣本,若且樣本數量大于問題維數(即|S|＞n),那么由所確定的PDE的體積將大于由所確定的PDE的體積.

推論2.對于選定的優秀樣本,到的馬氏距離越大,那么由所確定的PDE的體積越大.

證明.重新考慮式(11):證.

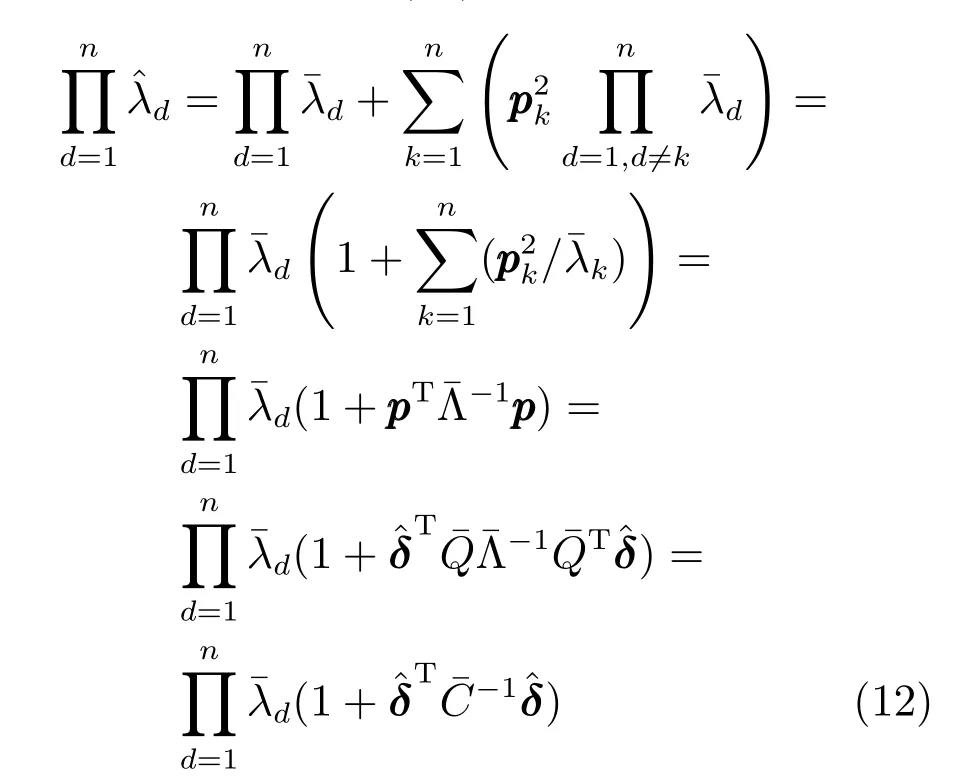
由上式可知,越大,越大.由此得

注1.推論1從理論上給出了保證由所確定的PDE的體積大于由所確定的PDE的體積的充要條件.由上文分析可知,GSM-GEDA在每次迭代中采用的通常不等于且優于;另一方面,GSM-GEDA及傳統GEDA通常都設置群體規模遠大于問題維數,那么從中選出的優秀樣本的數量一般都滿足|S|＞n.由此可知,GSM-GEDA能夠使推論1成立.這意味著,對于相同的選定樣本,GSM-GEDA的探索能力強于傳統GEDA.

注 2.推論2告訴我們,若要增強GSMGEDA 的探索能力,只需增大從到的馬氏距離也即增大對于選定的優秀樣本,是固定的.若要增大要求增大的各分量d(d=1,2,···,n),即在矩陣的各特征向量上的投影.根據式(6)可知,在優秀樣本選定的情況下,通過調整偏移系數ηf可以改變位置,進而調整的大小.ηf越大,傾向于增大,那么GSM-GEDA的探索能力會相應增強.

定理2.對于選定的優秀樣本,若,那么與由所確定的PDE長軸之間的夾角不大于其與由所確定的PDE長軸之間的夾角.

將n代入式(10)可知:

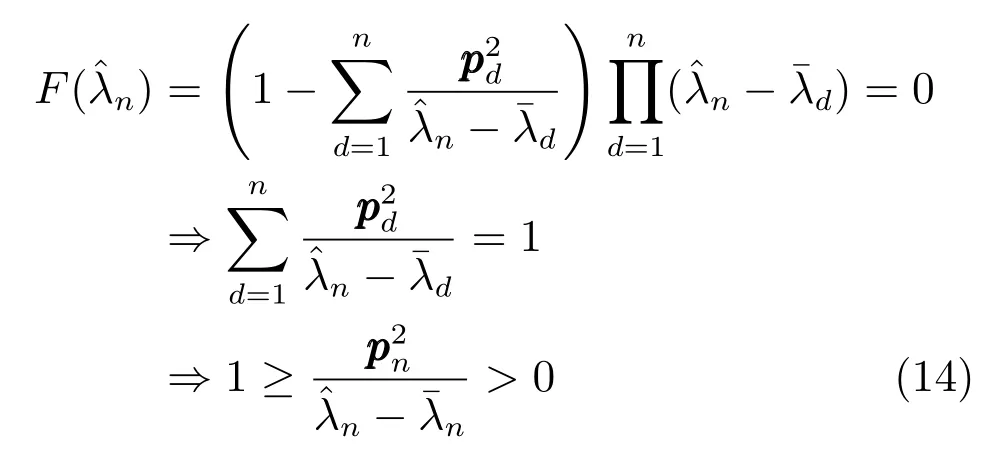
進一步有

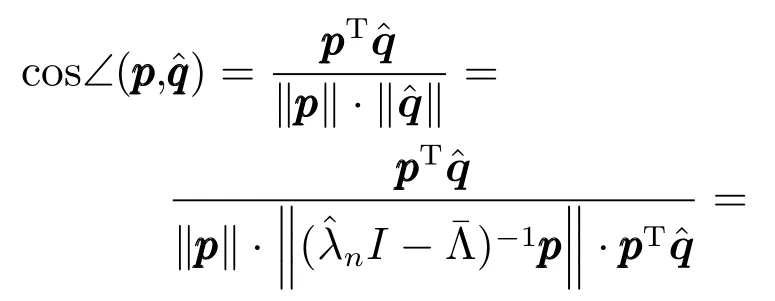
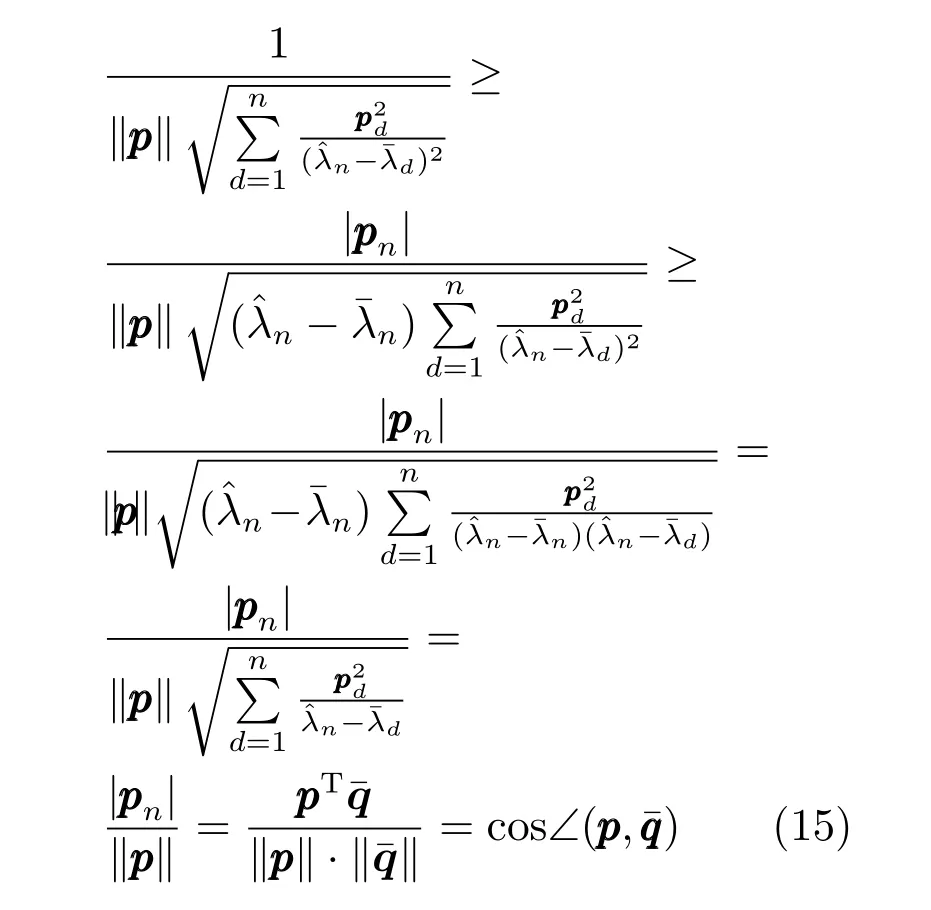
即由此可知,若定理2成立.

注3.在上述證明過程中,對于情況1可以推得依然分別是的特征值、特征向量;僅當較小,對其他特征值的調整幅度較小,使得仍為的主特征值時,才有對于情況2,僅當即時,才有因此,在絕大部分情況下,由于PDE的長軸,即CM的主特征向量決定了GEDA的主要搜索方向,那么定理2意味著,在采用作為CM的估計之后,GEDA的主要搜索方向更靠近目標函數的改進方向,因此更容易找到較優解.

2.3 GSM-GEDA的步驟

GSM-GEDA在基本EDA的框架之下,采用GPM描述優解的分布,并采用了一種新的GPM參數估計方法,其具體步驟如下:

步驟1.設置算法參數,包括群體規模m、優秀樣本比例系數τ以及前向偏移系數ηf;記迭代次數t=1,并采用偽均勻分布隨機生成m個解,初始化群體Mt.

步驟2.根據目標函數f(·)評價Mt中各個解的質量.

步驟3.根據截斷選擇規則,從Mt中選出前個優解,賦予優秀樣本集St.

步驟4.根據優秀樣本集St估計概率分布參數:1)根據式(4)計算加權的預估均值t;2)根據式(5)和(6)對t進行偏移,獲得最終的估計均值t;3)根據式(7)估計協方差矩陣t.

步驟5.根據高斯概率模型新生成m?2個解,并記由這些解構成的集合為采用精英策略更新群體

步驟6.更新t=t+1,判斷是否滿足終止條件.若滿足,則輸出最優結果;否則,轉至步驟2.

其中,步驟5采用常用的精英策略將當前群體中的最優個體保留到下一代群體中.此外,經過顯式評價后的t也可以看作一個完整的解樣本,并且其解質量通常較高,因此也將它保留到下一代群體中.

GSM-GEDA與傳統GEDA的區別主要體現在步驟4中的概率分布參數估計方法.從式 (4)～(7)可以看出,新提出的均值、CM 估計方法的計算時間復雜度分別為 O(τmn)=O(mn)、O(τmn2)=O(mn2),這與常用的 MLE的計算復雜度相同.這意味著GSM-GEDA可以以相同的計算復雜度獲得具有更好理論性質的GPM,即可以避免PDE快速收縮,從而保證算法具有適度的探索能力;并且可以使PDE的長軸方向趨近于目標函數的改進方向,進而提高算法的搜索效率.

3 實驗與分析

為了評估GSM-GEDA的性能,采用IEEE CEC 2005標準函數庫[27]中的前14個函數對其進行了測試.其中,f1～f5是單模函數,f6～f12是基本的多模函數,f13～f14是擴展的多模函數.這些函數大多都經過了旋轉、偏移操作,分別使得各變量之間相互關聯、最優解偏離搜索中心,從而保證函數的優化難度.在實驗中,所有函數的維數都設置為30,每個函數在每種算法上獨立測試25次,每次測試均以完成300000次目標函數評價作為終止條件,并采用所獲優解與實際最優解之間的差值(函數誤差值)在25次測試中的均值和標準差來衡量算法性能.

3.1 參數影響及其設置

GSM-GEDA一共包括3個參數,即群體規模m、優秀樣本比例系數τ以及前向偏移系數ηf.對于m和τ這兩個常規參數,文獻中已進行了較多研究[1,13],本文將其設置為常規值m=1200、τ=0.35.本節重點考察新參數ηf對GSM-GEDA的性能的影響.由第2節可知,ηf決定了預估均值eμ的偏移程度,從而改變PDE的中心位置、大小和長軸方向,最終影響GSM-GEDA的性能.

圖2以函數f2、f10為例,給出了當ηf以0.25為間隔從0.5增大到3.5時,GSM-GEDA的性能變化情況.從圖中可以看出,當ηf在0.5～3.5這么一個較大的范圍內變化時,GSM-GEDA的性能變化并不劇烈.特別地,對于f2,GSM-GEDA求得的解總是非常接近最優解.這說明GSM-GEDA的優化性能關于ηf的魯棒性較強.另一方面,在不考慮隨機因素的情況下,GSM-GEDA的性能總是隨著ηf的增大先變好后變差.對于f2這一單模函數,當ηf≈1.0時,GSM-GEDA取得較優結果;對于多模函數f10,當ηf≈2.75時,GSM-GEDA的表現較好.實驗表明,上述結論基本上也適用于其他測試函數.對于待優化的一般黑箱函數,并沒有先驗信息確定其為單模還是多模.為兼顧兩類函數的求解質量,我們建議在1.0～2.75之間為ηf取值;本文選取ηf=2.0.

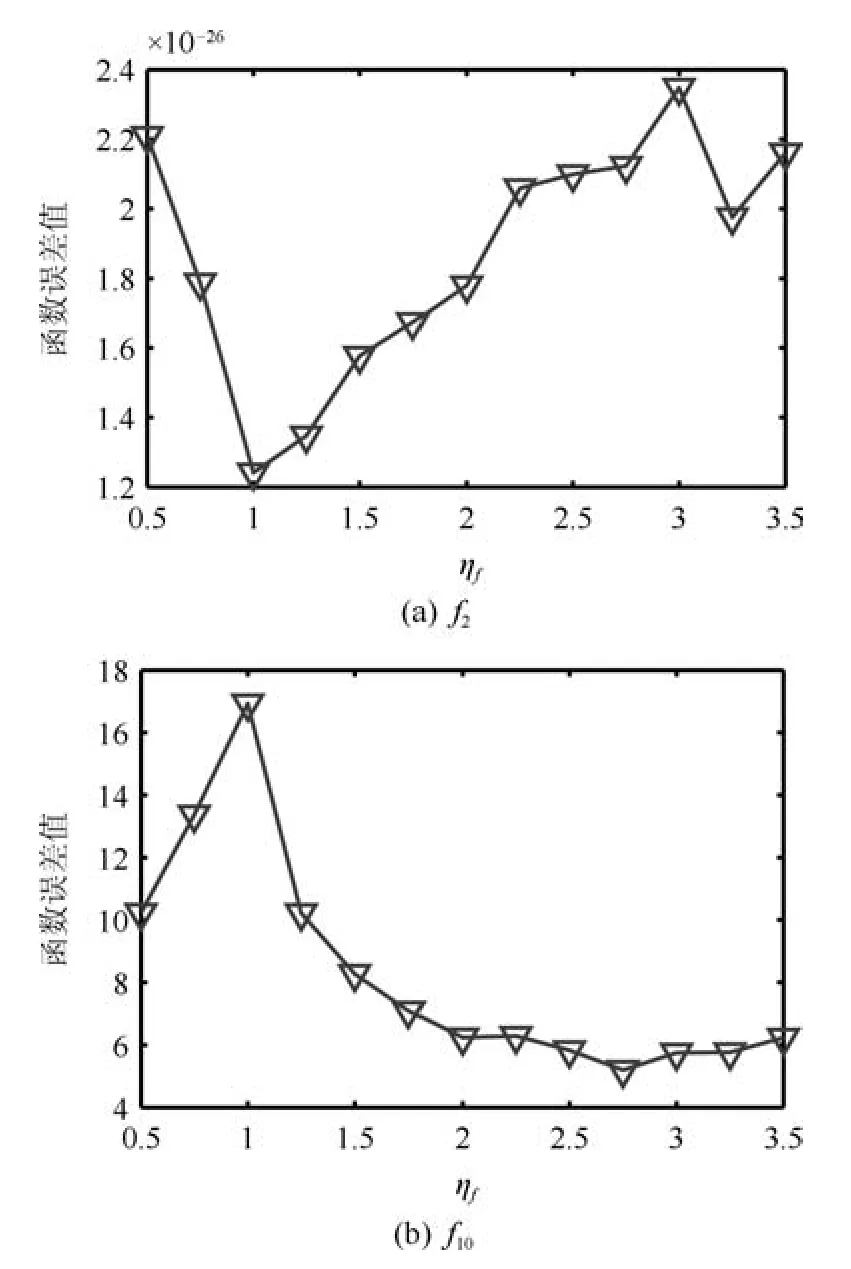
圖2 GSM-GEDA的性能隨ηf的變化情況Fig.2 The performance variation of GSM-GEDA with regard to ηf

3.2 均值?協方差矩陣估計方法的有效性分析

第2節理論證明了新提出的均值–協方差矩陣估計方法可以增大PDE的體積,使PDE的長軸方向趨近于目標函數的改進方向,本節將通過數值實驗驗證這一點.實驗設置如下:在GSM-GEDA的每次迭代中,除了根據式(4)～(7)所示的新方法估計CM 之外,還利用相同的優秀樣本,根據式(2)～(3)所示的傳統MLE方法估計CM,從而滿足定理1和2的限定條件.為描述方便,將這種依附于GSM-GEDA但采用傳統估計方法的算法稱為quasi-GSM-GEDA.此外,還將EMNAg[1]作為對比算法.除參數估計方法之外,EMNAg的其他設置與GSM-GEDA完全相同.

圖3和4以函數f2、f10為例,分別給出了各算法的PDE的長軸長度、長軸與目標函數改進方向之間的夾角余弦(簡記為cos(A1))隨迭代次數的變化情況.從圖3中可以看出,GSM-GEDA和quasi-GSM-GEDA的PDE的長軸長度都隨迭代次數的增大而逐漸減小,但前者的長度始終不小于后者,該現象在前期迭代過程中尤為明顯.實際上,上述結論對于PDE的其他軸也是成立的,這與定理1所述內容一致.從圖4中可以看出,GSM-GEDA的cos(A1)值始終不小于quasi-GSM-GEDA的相應值,這說明GSM-GEDA的PDE的長軸與之間的夾角不大于quasi-GSM-GEDA的相應夾角,這與定理2所述內容一致.

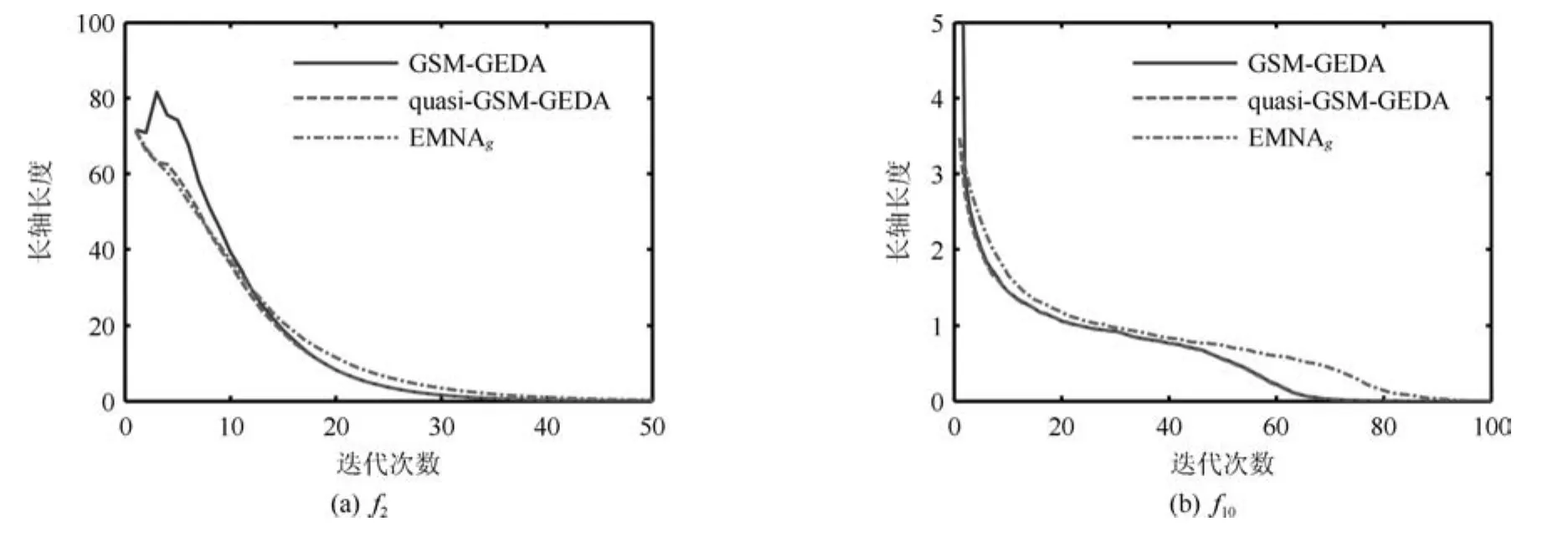
圖3 長軸長度隨迭代次數的變化情況Fig.3 The variation of long axis length with regard to iteration times

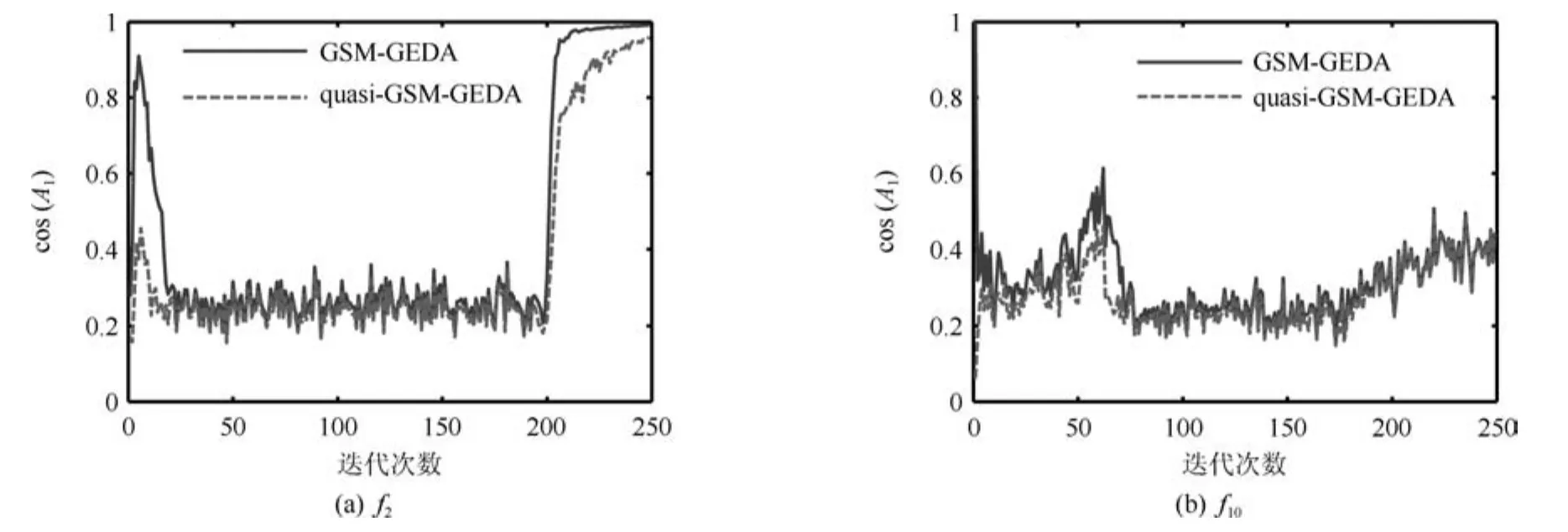
圖4 長軸與目標函數改進方向之間的夾角余弦隨迭代次數的變化情況Fig.4The variation of the cosine value of the angle between long axis and with regard to iteration times

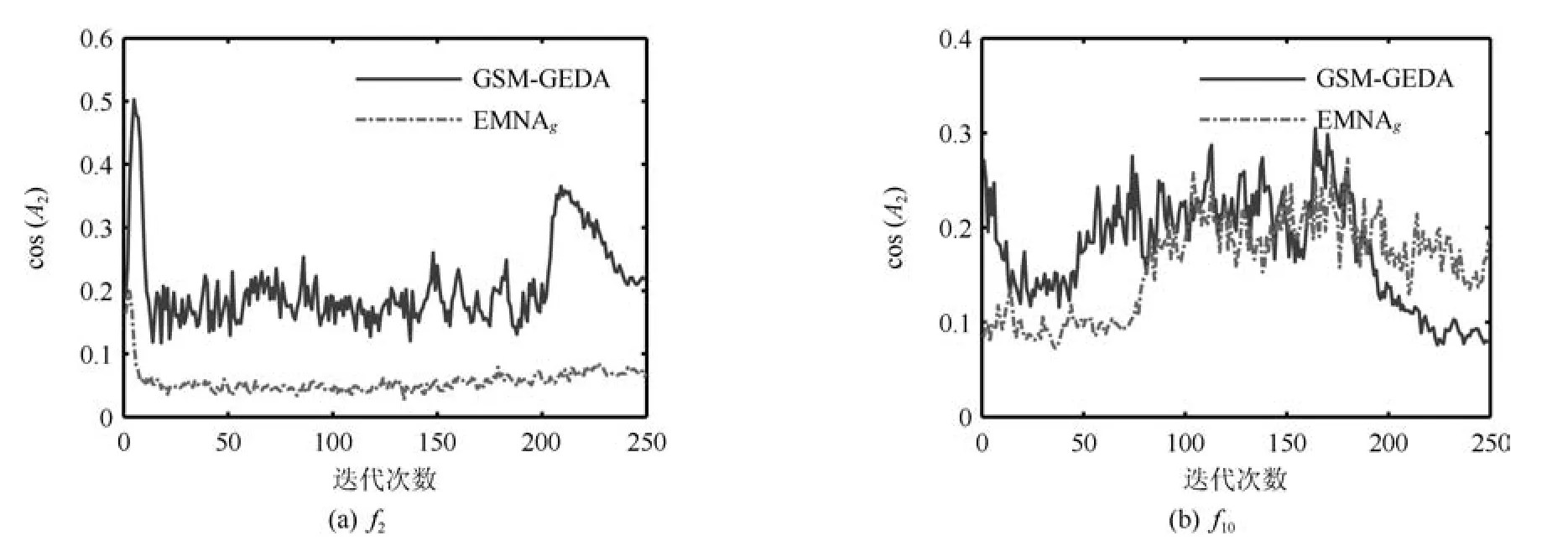
圖5 長軸與最速下降方向之間的夾角余弦隨迭代次數的變化情況Fig.5 The variation of the cosine value of the angle between long axis and the steepest descent direction with regard to iteration times

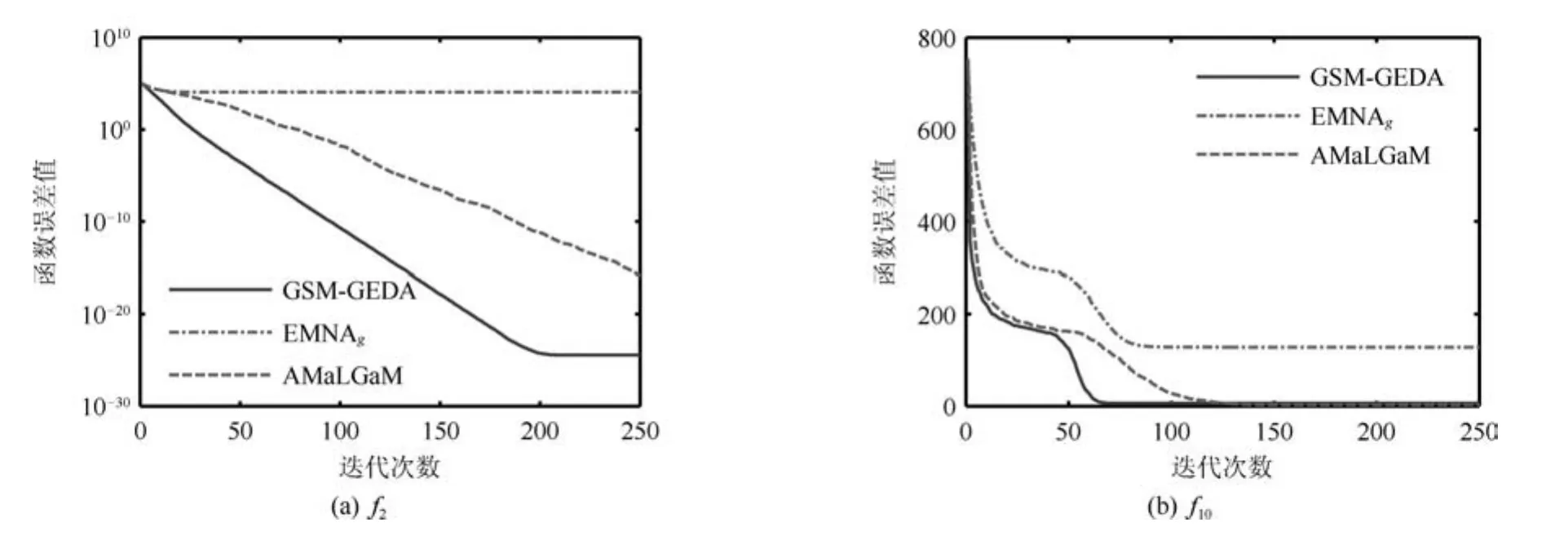
圖6 函數誤差值隨迭代次數的變化情況Fig.6 The variation of the function error value with regard to iteration times

從圖3中還可以看出,與EMNAg相比,GSMGEDA的PDE的長軸長度在前期迭代過程中保持了較大值,這有利于算法進行探索性搜索;在中后期迭代過程中,GSM-GEDA的PDE的長軸收縮到一個較小的尺度范圍內,這有利于算法進行精細搜索.為了進一步說明GSM-GEDA與EMNAg的性能差異,圖5和6分別給出了兩算法的PDE的長軸與目標函數的最速下降方向(即從PDE的中心指向最優解的方向)之間的夾角余弦(簡記為cos(A2))、所求得的最小函數誤差值隨迭代次數的變化情況.從圖5中可以看出,對于f2這一單模函數,GSMGEDA的cos(A2)值始終大于EMNAg的相應值,說明GSM-GEDA能夠探測到較好的搜索方向.從圖6中可以看出,GSM-GEDA在經過大概200次迭代后基本上獲得了f2的最優解;EMNAg在經過大概15次迭代后便早熟收斂,無法獲得理想解.對于多模函數f10,GSM-GEDA在中前期迭代過程中的cos(A2)值也大于EMNAg的相應值,盡管兩算法都陷入了局部優解,但GSM-GEDA獲得的終解遠優于EMNAg.

圖6還給出了AMaLGaM[13]獲得的最小函數誤差值的進化情況.AMaLGaM利用預期均值偏移策略和自適應方差縮放策略改進了傳統GEDA,是當前性能最為優越的EDA之一.從圖6中可以看出,AMaLGaM和GSM-GEDA在不同程度上消弱了EMNAg的早熟收斂問題.在給定的目標函數評價次數內,GSM-GEDA求得的f2、f10的終解分別優于、接近于AMaLGaM所得結果,其收斂速度也快于AMaLGaM.

3.3 與其他算法的比較

為了綜合衡量GSM-GEDA的性能,將其與 6種已有算法進行了比較,包括 EMNAg[1]、AMaLGaM[13]、 CMA-ES[28]、 CLPSO[29]、CoBiDE[30]以及MPEDE[31].選擇這6種算法作為對比算法的原因在于:EMNAg和AMaLGaM分別是傳統GEDA和先進GEDA的典型代表,可以為衡量GSM-GEDA的性能提供基準;CMAES、CLPSO、CoBiDE分別是進化策略算法、粒子群算法、差分進化算法的代表算法,并被多次用作對比算法,而且CoBiDE中的交叉算子也涉及了CM的估計問題;MPEDE是一種新近提出的差分進化算法,一定程度上反映了當前函數智能優化方面的發展水平.

為了保證比較的公平性,EMNAg、AMaLGaM以及GSM-GEDA的參數m、τ取為相同值,AMaLGaM 也選用全變量相關的GPM 模型;AMaLGaM的其余參數以及其他4種算法的參數均按照相應的原文獻進行取值.表1給出了各算法最終所獲優解的函數誤差值在25次獨立測試中的均值和標準差,表中還采用了下式所示的Cohen′sd效應量[32]衡量GSM-GEDA與其他6種算法之間的性能差異:

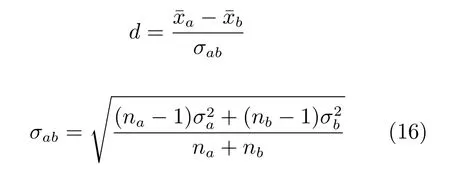
其中,分別表示樣本集a的均值、標準差、樣本數量.通常當|d|＜0.2時,認為兩樣本集的均值差異較小[32],這里意味著兩個被測算法的性能無顯著差異,在表1中用符號“≈”標識.反過來,若根據效應量判斷出某算法顯著優于或差于GSM-GEDA,則在表1中分別用符號“+”、“?”來標識.

從表1中可以看出,對于單模函數f1～f5,GSM-GEDA的性能比較理想.盡管針對f1、f2的優化結果差于差分進化算法,但其獲得的解也已充分接近最優解.對于基本的多模函數f6～f12,GSM-GEDA在3個函數上的性能優于其他所有算法;特別地,它可以獲得f7、f11的最優解.對于f6、f9,3種EDA的表現都不太理想;對于f8,所有被測算法的性能差異不大;對于f10,GSM-GEDA的表現僅次于AMaLGaM,優于其他5種算法.對于擴展的多模函數,GSM-GEDA在f13上的表現與CoBiDE接近,僅次于CLPSO;在f14上的表現優于其他所有算法.根據表1最后一行的統計結果可知,GSM-GEDA 分別在14、9、12、9、9、9個函數上的性能顯著優于EMNAg、AMaLGaM、CMAES、CLPSO、CoBiDE、MPEDE,表現出良好的全局尋優能力.

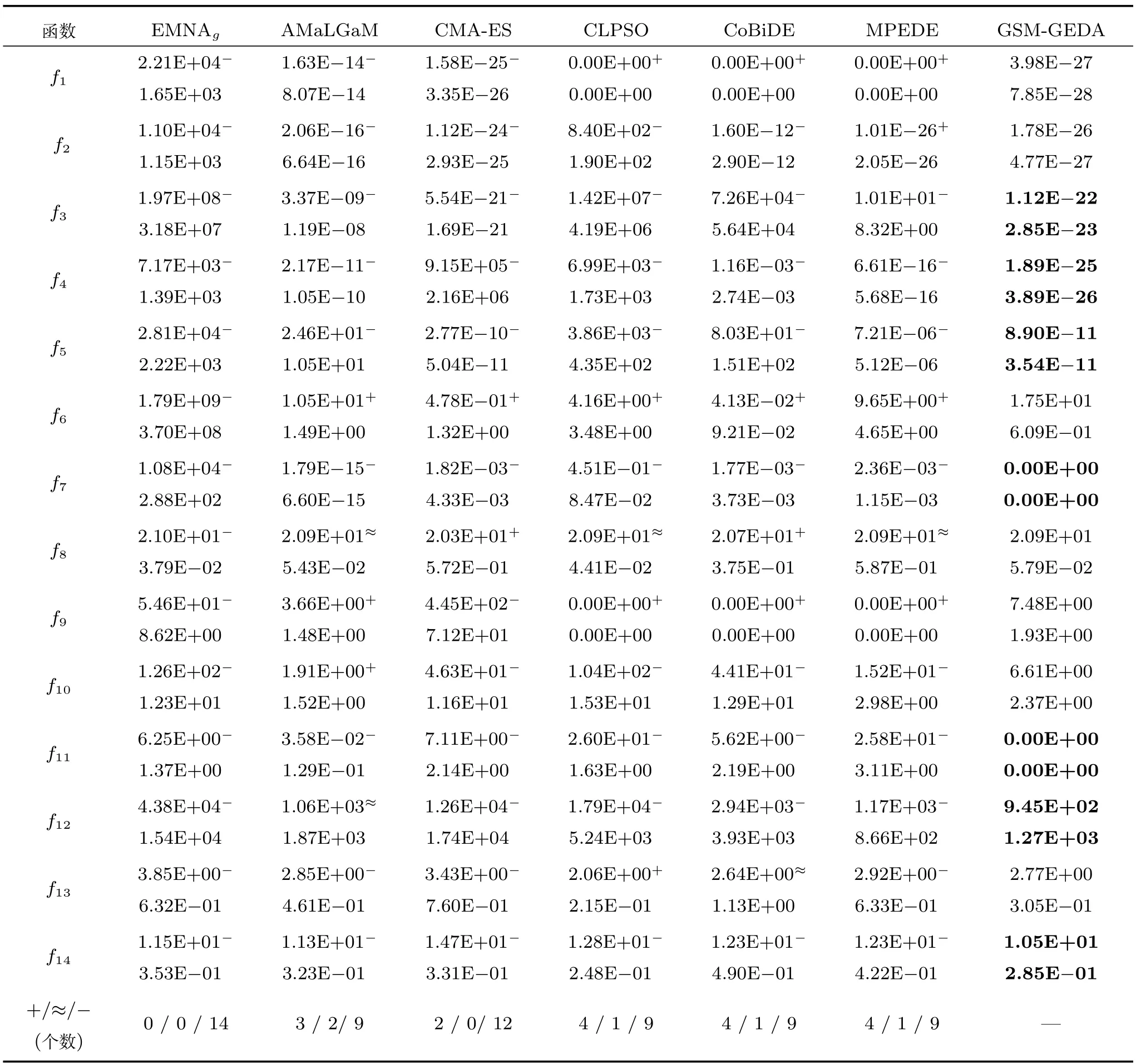
表1 7種算法最終求得的函數誤差值的均值和標準差Table 1 The mean and standard deviation of the function error values obtained by 7 algorithms

4 結論

概率密度橢球體(PDE)的位置、大小和長軸方向是影響高斯分布估計算法(GEDA)性能的關鍵.本文在分析傳統GEDA性能弱化原因的基礎上,提出了一種基于一般二階混合矩的高斯分布估計算法(GSM-GEDA).該算法以沿目標函數改進方向偏移后的加權均值作為協方差矩陣(二階混合中心矩)的矩中心,一方面將PDE引導至一個更有希望的解區域;另一方面可以自適應地增大PDE的大小,并使PDE的長軸方向趨近于目標函數的改進方向.理論分析和數值實驗均證明了上述結論的正確性.此外,在14個標準函數上的數值測試還表明,GSM-GEDA的求解質量優于現有的GEDA以及其他一些先進的進化算法.下一步工作將研究設計更為系統化的均值偏移策略,并在實際的復雜優化問題中檢驗GSM-GEDA的有效性.

References

1 Larranaga P,Lozano J A.Estimation of Distribution Algorithms:A New Tool for Evolutionary Computation.New York,USA:Springer,2001.57?100

2 Hauschild M,Pelikan M.An introduction and survey of estimation of distribution algorithms.Swarm and Evolutionary Computation,2011,1(3):111?128

3 Wang Sheng-Yao,Wang Ling,Fang Chen,Xu Ye.Advances in estimation of distribution algorithms.Control and Deci-sion,2012,27(7):961?966,974(王圣堯,王凌,方晨,許燁.分布估計算法研究進展.控制與決策,2012,27(7):961?966,974)

4 Larraaga P,Etxeberria R,Lozano J A,Pe?na J M.Optimization in continuous domains by learning and simulation of Gaussian networks.In:Proceedings of 2000 Genetic and Evolutionary Computation Conference.Las Vegas,USA:Morgan Kaufmann,2000.201?204

5 Lu Q,Yao X.Clustering and learning Gaussian distribution for continuous optimization.IEEE Transactions on Systems,Man,and Cybernetics,Part C:(Applications and Reviews),2005,35(2):195?204

6 Yuan B,Gallagher M.On the importance of diversity maintenance in estimation of distribution algorithms.In:Proceedings of the 7th Annual Conference on Genetic and Evolutionary Computation.New York,USA:ACM,2005.719?726

7 Po?k P.Preventing premature convergence in a simple EDA via global step size setting.Parallel Problem Solving from Nature—PPSN X.Lecture Notes in Computer Science.Berlin,Heidelberg,Germany:Springer-Verlag,2008:.549?558

8 Dong W S,Yao X.Uni fied Eigen analysis on multivariate Gaussian based estimation of distribution algorithms.Information Sciences,2008,178(15):3000?3023

9 Ocenasek J,Kern S,Hansen N,Koumoutsakos P.A mixed bayesian optimization algorithm with variance adaptation.Parallel Problem Solving from Nature—PPSN VIII.Lecture Notes in Computer Science.,Berlin,Heidelberg,Germany:Springer-Verlag,2004.352?361

10 Bosman P A N,Grahl J,Rothlauf F.SDR:a better trigger for adaptive variance scaling in normal EDAs.In:Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation.New York,USA:ACM,2007.492?499

11 Cai Y P,Sun X M,Xu H,Jia P F.Cross entropy and adaptive variance scaling in continuous EDA.In:Proceedings of the 9th Annual Conference on Genetic and Evolutionary Computation.New York,USA:ACM,2007.609?616

12 Bosman P A N,Grahl J,Thierens D.Enhancing the performance of maximum-likelihood Gaussian EDAs using anticipated mean shift.Parallel Problem Solving from Nature—PPSN X.Lecture Notes in Computer Science.Berlin,Heidelberg,Germany:Springer-Verlag,2008:.133?143

13 Bosman P A N,Grahl J,Thierens D.Benchmarking parameter-free AMaLGaM on functions with and without noise.Evolutionary Computation,2013,21(3):445?469

14 Cheng Yu-Hu,Wang Xue-Song,Hao Ming-Lin.An estimation of distribution algorithm with diversity preservation.Acta Electronica Sinica,2010,38(3):591?597(程玉虎,王雪松,郝名林.一種多樣性保持的分布估計算法.電子學報,2010,38(3):591?597)

15 Karshenas H,Santana R,Bielza C,Larra?naga P.Regularized continuous estimation of distribution algorithms.Applied Soft Computing,2013,13(5):2412?2432

16 Yang P,Tang K,Lu X F.Improving estimation of distribution algorithm on multi-modal problems by detecting promising areas.IEEE Transactions on Cybernetics,2015,45(8):1438?1449

17 Ding N,Zhou S D,Sun Z Q.Histogram-based estimation of distribution algorithm:a competent method for continuous optimization.Journal of Computer Science and Technology,2008,23(1):35?43

18 Zhang Jian-Hua,Zeng Jian-Chao.Estimation of distribution algorithm based on sequential importance sampling particle filters.Acta Electronica Sinica,2010,38(12):2929?2932(張建華,曾建潮.基于序貫重點采樣粒子濾波的分布估計算法.電子學報,2010,38(12):2929?2932)

19 Wang Li-Fang,Zeng Jian-Chao,Hong Yi.Estimation of distribution algorithm modeling and sampling by means of Copula.Control and Decision,2011,26(9):1333?1337,1342(王麗芳,曾建潮,洪毅.利用Copula函數估計概率模型并采樣的分布估計算法.控制與決策,2011,26(9):1333?1337,1342)

20 Zhou A M,Sun J Y,Zhang Q F.An estimation of distribution algorithm with cheap and expensive local search.IEEE Transactions on Evolutionary Computation,2015,19(6):807?822)

21 Zhang Fang,Lu Hua-Xiang.General stochastic model for algorithm of distribution estimation with conditional probabilities and Gibbs sampling.Control Theory&Applications,2013,30(3):307?315(張放,魯華祥.利用條件概率和Gibbs抽樣技術為分布估計算法構造通用概率模型.控制理論與應用,2013,30(3):307?315)

22 Zhong Wei-Cai,Liu Jing,Liu Fang,Jiao Li-Cheng.Estimation of distribution algorithm based on generic Gaussian networks.Journal of Electronics and Information Technology,2005,27(3):467?470(鐘偉才,劉靜,劉芳,焦李成.建立在一般結構Gauss網絡上的分布估計算法.電子與信息學報,2005,27(3):467?470)

23 Zhao Hong.Areas(Volumes)ofn-dimension ellipsoid by quadratic curve(surface)enclosed.Mathematics in Practice and Theory,2013,43(10):279?282(趙虹.n元橢球面的判定及所圍橢球體的體積.數學的實踐與認識,2013,43(10):279?282)

24 Bunch J R,Nielsen C P,Sorensen D C.Rank-one modi fication of the symmetric eigenproblem.Numerische Mathematik,1978,31(1):31?48

25 Yin Qing-Xiang.The inverse problem of rank-1 modi fication of real symmetric matrices.Journal of Nantong Institute of Technology(Natural Science),2003,2(4):11?14(殷慶祥.實對稱矩陣的秩1修正的特征反問題.南通工學院學報(自然科學版),2003,2(4):11?14)

26 Xie Ping-Min,Chen Tu-Hao.The positive de finiteness of the covariance matrix of continuous sample.Acta Scientiarum Naturalium Universitatis Sunyatseni,1990,29(1):102?104(謝平民,陳圖豪.連續型樣本協差陣的正定性.中山大學學報(自然科學版),1990,29(1):102?104)

27 Suganthan P N,Hansen N,Liang J J,Deb K,Chen Y P,Auger A,Tiwari S.Problem De finitions and Evaluation Criteria for the CEC 2005 Special Session on Real Parameter Optimization,Technical Report,Nanyang Technological University,Singapore,2005.

28 Hansen N,Ostermeier A.Completely derandomized selfadaptation in evolution strategies.Evolutionary Computation,2001,9(2):159?195

29 Liang J J,Qin A K,Suganthan P N,Baskar S.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions.IEEE Transactions on Evolutionary Computation,2006,10(3):281?295

30 Wang Y,Li H X,Huang T W,Li L.Differential evolution based on covariance matrix learning and bimodal distribution parameter setting.Applied Soft Computing,2014,18:232?247

31 Wu G H,Mallipeddi R,Suganthan P N,Wang R,Chen H K.Differential evolution with multi-population based ensemble of mutation strategies.Information Sciences,2016,329:329?345

32 Cohen J.Statistical Power Analysis for the Behavioral Sciences(Second Edition).Hillsdale,NJ:Lawrence Erlbaum Associates,1988.