基于Matlab/Simulink的滾動軸承劃傷缺陷動力學建模及仿真*

何貞志，徐曉冬，邵明輝

(1.江蘇師范大學 機電工程學院，江蘇 徐州 221116；2.蘭州理工大學 能源與動力工程學院，甘肅 蘭州 730050)

0 引 言

滾動軸承廣泛應用于旋轉機械中，軸承缺陷是引起機械故障的重要因素之一。軸承缺陷包括兩大類：分布式缺陷和局部式缺陷。一般來說，軸承劃傷缺陷是引起軸承失效的主要原因。

軸承劃傷缺陷的振動響應模型是為了研究缺陷對軸承沖擊引起的軸承振動響應，在軸承結構振動模型的基礎上提出的一種軸承振動簡化模型[1]。對軸承缺陷模型的建立主要存在以下方法：

(1)局部式缺陷的沖擊序列模型。MCFADDEN等[2-3]使用一串串周期性脈沖函數模擬單點和多點局部式缺陷對軸承振動的影響，使用脈沖函數中的放大系數表示缺陷的沖擊程度；CHOUDHURY等[4]使用沖擊力序列模擬軸承局部式缺陷的激勵作用，該沖擊力激起了內圈、外圈等軸承元件的共振模態；陳於學等[5]利用脈沖沖擊波模擬滾動軸承早期缺陷振動；曹宏瑞等[6]、武濟鋼等[7]利用一系列沖擊脈沖描述滾動體經過損傷時產生的沖擊現象。

(2)軸承系統的多體動力學模型，這種模型建立軸承系統的非線性動力學模型，并對其進行求解得到軸承系統的振動響應，將軸承缺陷引起的軸承元件間的附加趨近量添加到正常情況下的彈性趨近量中，根據Hertz接觸理論計算接觸載荷。ARSLAN等[8]建立了軸承-轉子系統的動力學模型，研究了局部式缺陷引起的角接觸球軸承的振動特性；PATEL等[9]考慮局部式缺陷的寬度和深度建立了套圈含局部式缺陷的滾動軸承動力學模型；MOAZEN等[10]考慮滾動體的質量建立了滾動軸承非線性動力學模型，研究了局部式缺陷對接觸載荷及振動的影響。

本文將通過引入劃傷缺陷引起軸承內、外圈之間額外彈性趨近量，利用余弦函數建立內圈劃傷、外圈劃傷的缺陷模型，從而得到劃傷缺陷滾動軸承外圈的非線性動力學模型，并基于Simulink進行仿真求解，得到外圈的缺陷振動響應，同時對振動特性進行分析，為滾動軸承振動仿真分析及故障診斷提供理論依據。

1 滾動軸承劃傷缺陷動力學模型

假設軸承內圈以恒速旋轉，外圈在外加徑向載荷Fr的作用下不轉動。本研究在建立滾動軸承振動模型時，忽略滾動體的質量，將滾動體與外圈和內圈間的接觸采用彈簧和阻尼來代替，討論軸承的振動特性，軸承的振動模型如圖1所示。

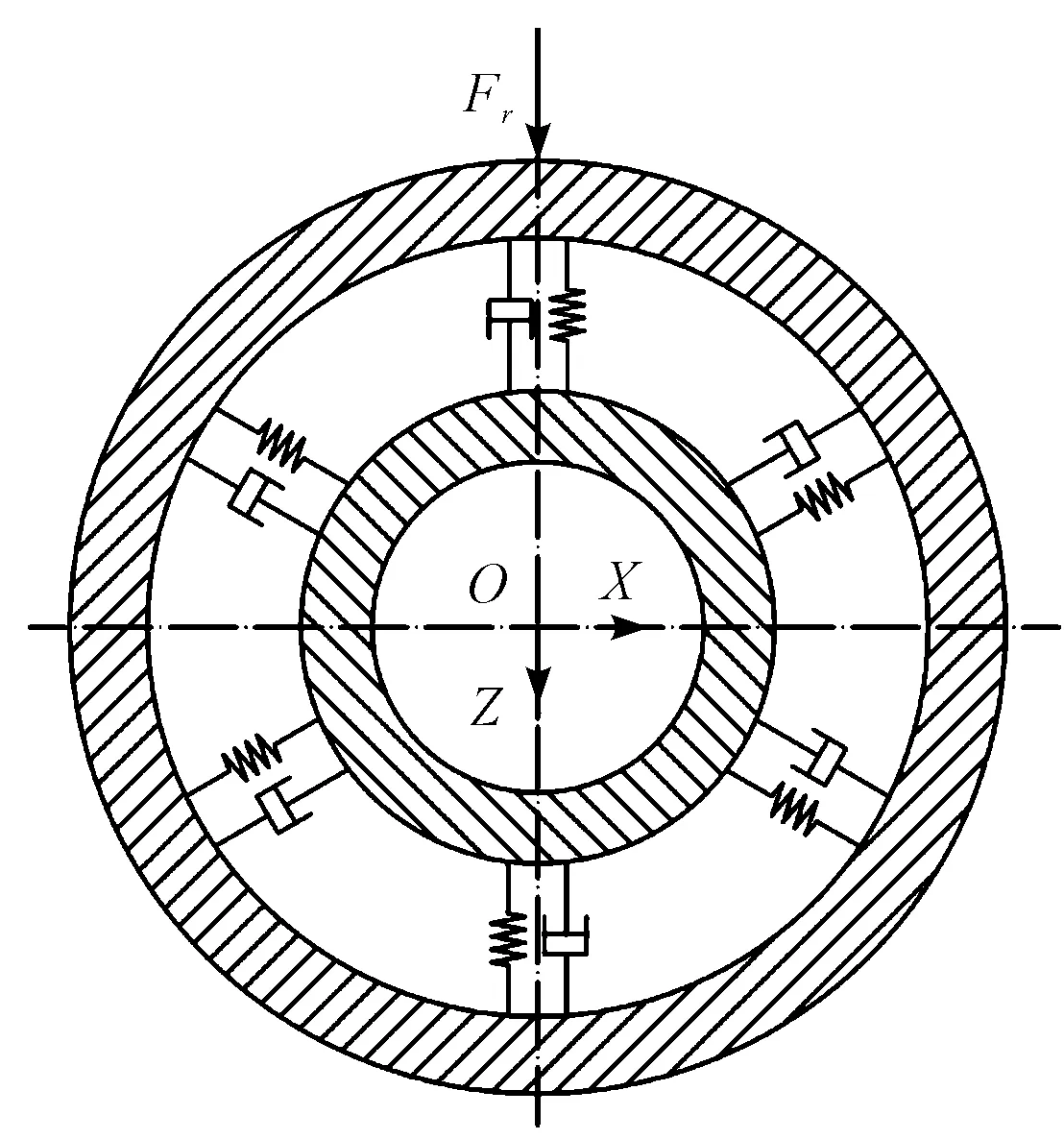
圖1 軸承的振動模型

假設滾動體勻速轉動，則t時刻第j個滾動體的方位角可以寫為：

(1)

式中：ωc—保持架轉動角頻率；φ0—首個滾動體的初始方位角；Z—滾動體個數。

1.1 接觸變形量

考慮無缺陷軸承中的接觸情況。根據圖1所示的球軸承振動模型，在外界因素的作用下，軸承轉動過程中內、外圈滾道與滾動體之間產生接觸變形，方位角φj處的正常軸承內、外圈滾道的相對趨近量δj可以表示為：

δj=-xsinφj-zcosφj-Cr

(2)

式中：Cr—滾動軸承的徑向間隙。

若軸承元件中存在缺陷，當缺陷位于滾動體與內、外圈滾道的接觸區域時，缺陷的存在將產生額外的彈性趨近量δ′。

滾動軸承內、外圈滾道表面劃傷缺陷模型如圖2所示。

圖2 劃傷缺陷示意圖

此處假設缺陷為早期劃傷缺陷，即缺陷寬度較小，滾動體經過劃傷缺陷時不與缺陷底部接觸。

當滾動體進入損傷區域時，其和滾道之間由于缺陷產生的額外趨近量可使用余弦函數表示為[11]：

(3)

式中：v—接觸零件之間移動的相對速度；wd—缺陷寬度；φd0—缺陷初始方位角；φj，φd—滾動體和缺陷的瞬時方位角；φ—缺陷范圍角，φ≈2wd/d；d—劃傷缺陷所在滾道的直徑(內圈或外圈滾道)；Δ—缺陷引起趨近量的幅值。

Δ大小由缺陷嚴重程度及軸承幾何尺寸決定：

(4)

式中：“+”—內圈劃傷情況；“-”—外圈劃傷情況；φb≈2wd/Db；Db——滾動體直徑。

此時，內、外圈間的總接觸變形量為原接觸變形與缺陷引起的內、外圈額外趨近量之和，即：

δej=δj+δ′

(5)

1.2 接觸載荷和阻尼力

在滾動軸承的接觸問題分析中，只有當滾子和內、外圈滾道接觸時才產生接觸載荷Qsj，因此，本研究將接觸載荷表示為分段函數，即當接觸變形量為正值時才存在接觸載荷，否則接觸載荷為0。根據Hertz接觸理論，方位角φj處內、外圈的接觸載荷Qsj可表示為[12]：

(6)

式中：Kn—內、外圈等效載荷-變形系數；n—載荷-變形指數。

對球軸承，n=3/2；對滾子軸承，n=10/9。

同樣的，接觸副間的阻尼力Qdj可以寫為：

(7)

式中：c—等效粘性阻尼系數。

1.3 軸承外圈動力學方程

根據圖1可以得到軸承外圈X向和Z向的運動微分方程分別為：

(8)

(9)

式中：mo—外圈質量；Fr—施加在外圈上的徑向載荷；Z—滾子個數；Qsj，Qdj—方位角φj處內、外圈接觸副間接觸載荷和阻尼力，分別由式(6，7)給出。

2 Simulink動力學仿真模型

Matlab是當今較流行的以數值計算為主的軟件，其中自帶的仿真工具包Simulink可以較為方便地按照給定方程對動力學系統進行建模、仿真求解和分析。用戶既可用方框圖建立仿真模型[13]，也可以使用Matlab語言編寫M文件構建模型。與傳統的仿真軟件相比，Simulink具有直觀、方便、靈活的特點。

利用Simulink進行數值仿真的一般步驟為：建立系統的數學模型；在Simulink中建立數字仿真模型并設置仿真參數[14]；執行仿真得出仿真結果并分析。

2.1 建立仿真模型

使用標準的積分模塊，根據軸承外圈x向和z向加速度得到相應的速度、位移狀態，根據式(8，9)可以得到Simulink環境下的滾動軸承劃傷缺陷動力學模型，如圖3所示。

其中，為了使程序框圖整潔、易理解，模型中使用了Subsystem、From、Goto、Bus Creator、Bus Selector等模塊。

其中，ForceSum模塊的功能是根據每個滾子位置處的接觸彈性力Qsj和阻尼力Qdj計算x向和z向總接觸載荷，如圖4所示。

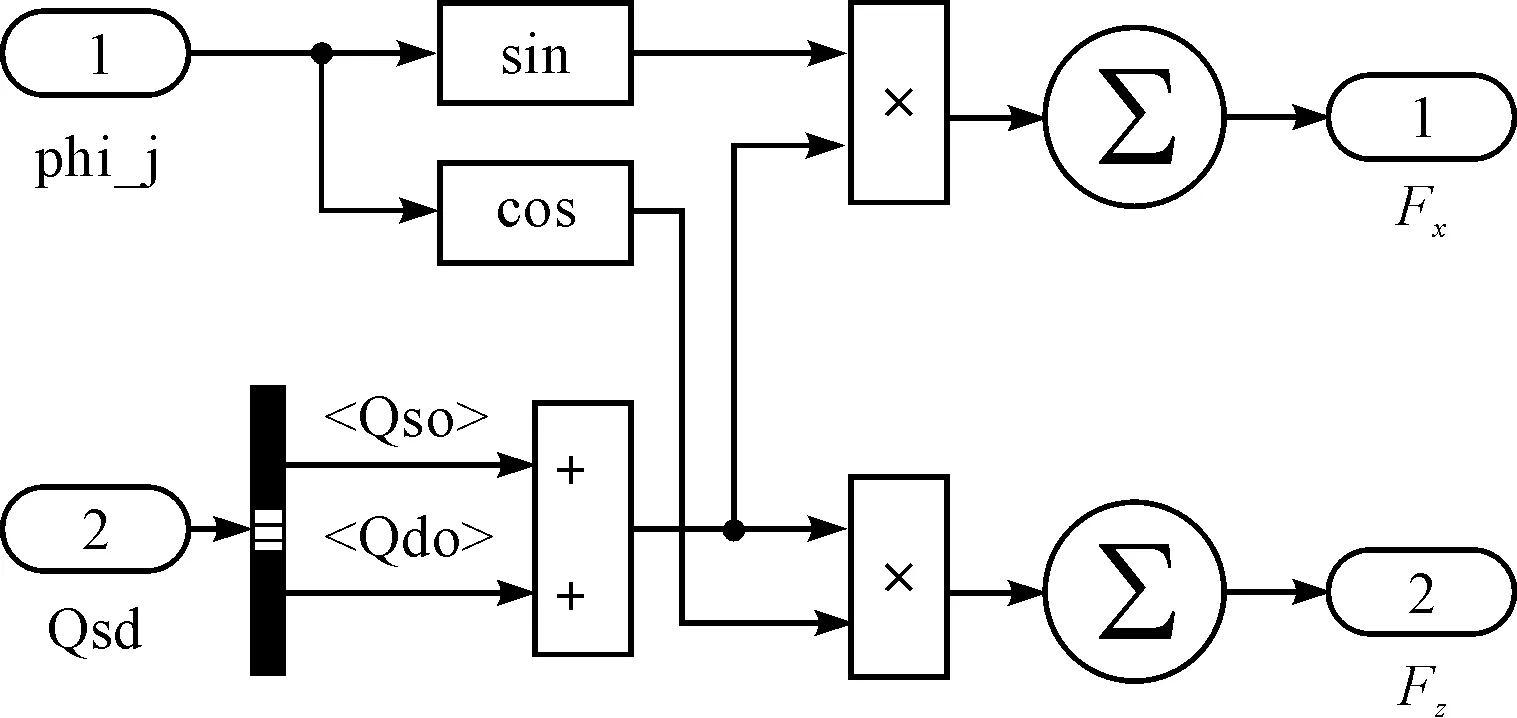
圖4 計算總接觸載荷的ForceSum模塊

根據軸承外圈、內圈之間的相互位置關系及劃傷缺陷模型，由式(2，5)可計算各滾子處的接觸變形量δj，根據接觸載荷的計算公式(6，7)，得到軸承外圈的接觸載荷，如圖5所示。

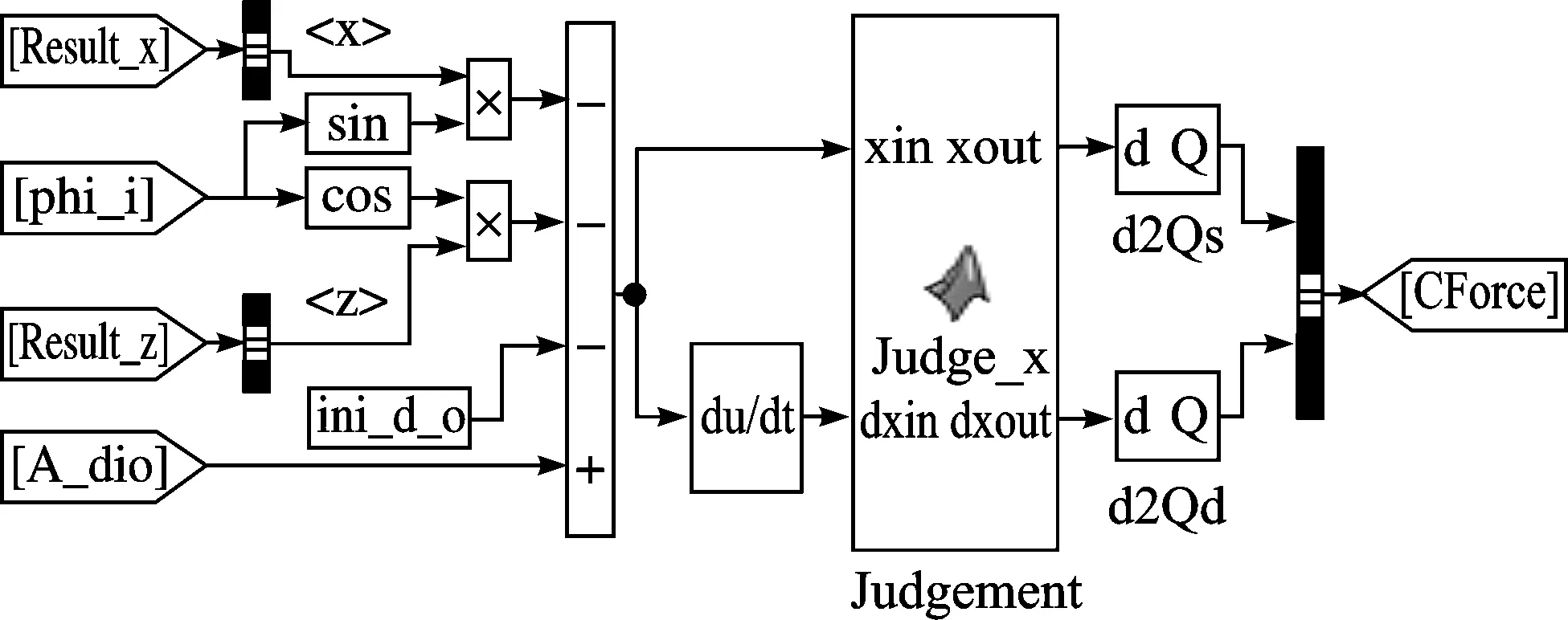
圖5 各滾子處接觸載荷的計算

在滾動軸承動力學問題中的載荷為接觸載荷，僅當軸承元件接觸時存在載荷，即該接觸載荷為分段函數，如式(6，7)所示。使用Simulink標準模塊可以對此進行建模，但模型將比較復雜。因此使用Matlab function實現模型中的分段函數，具有簡單直觀的特點，如圖5中Judgement模塊所示。

2.2 設置仿真參數

利用Simulink對動力學模型進行仿真，需要對仿真參數進行合理的設置：

(1)仿真時間的設置。開始時間為0 s，停止時間為0.2 s；

(2)求解器類型的選擇。選擇Variable-step變步長、ode45算法；

(3)初始值的設置。x、z的積分初值設置為靜力平衡情況下的x0、z0。

3 仿真結果及分析

以某型號球軸承為例，主要參數如表1所示。

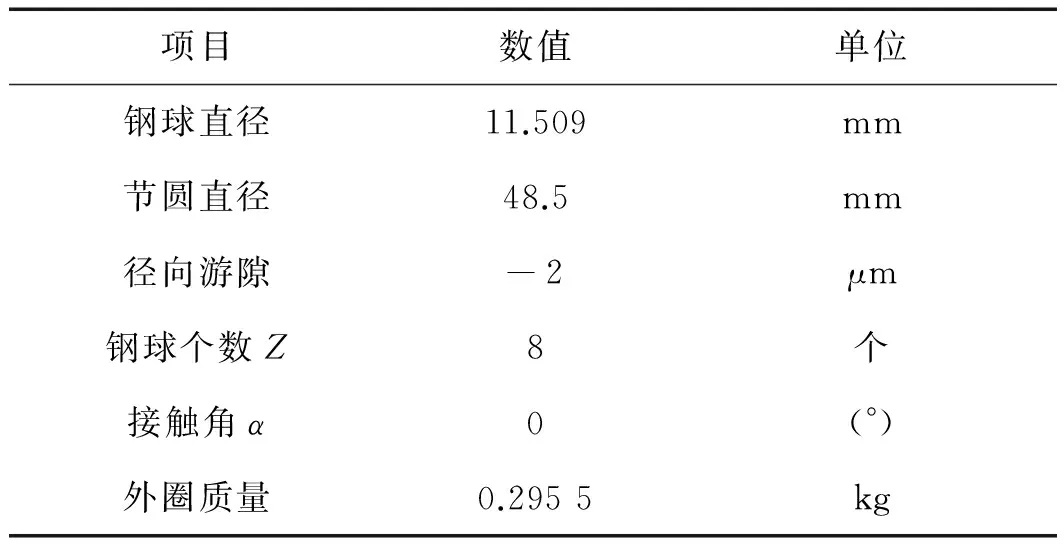
表1 球軸承主要參數

其中，徑向載荷為1 000 N，主軸轉速(內圈轉速)為1 500 r/min，可得內圈轉動頻率ωs為25 Hz。對于內圈旋轉、外圈不轉動的軸承，當軸承內圈滾道、外圈滾道存在缺陷時，根據幾何關系可得到滾動體通過內圈滾道或外圈滾道上一個缺陷的通過頻率，即內圈缺陷頻率、外圈缺陷頻率，分別表示為：

(10)

(11)

因此，可得保持架轉動頻率ωc為9.5 Hz，外圈缺陷頻率ωo為76.3 Hz，內圈缺陷頻率ωi為123.7 Hz。

3.1 正常軸承仿真結果

滾動軸承無缺陷時，利用Simulink仿真得到的內圈-外圈接觸變形量及接觸載荷的變化、軸承外圈Z向的加速度響應如圖6所示。

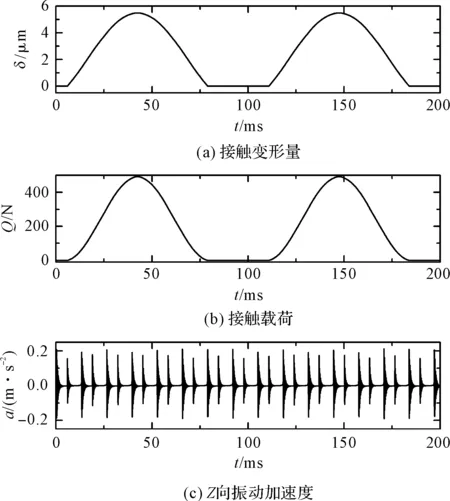
圖6 正常軸承振動響應

由圖6可知：

(1)在徑向載荷作用下，軸承中某一滾動體處的內圈-外圈接觸變形量和接觸載荷均呈周期性變化，如圖6(a，b)所示；

(2)在軸承轉動過程中，某一滾動體并不是始終與內圈、外圈接觸，存在脫離接觸的情況，即圖中接觸變形量及接觸載荷為零的時刻，該時間與徑向載荷、軸承結構及游隙等有關，如圖6(a，b)所示；

(3)正常軸承外圈Z向存在周期性的低幅振動(最大幅值約為0.2 m/s2)，其周期為滾動體通過頻率，如圖6(c)所示。實際上，這種振動是由于使用了有限個滾動體支撐方式，在軸承運轉過程中，鋼球的方位角是不斷變化的，導致軸承承載區內的承載鋼球數目及承載力周期性變化，軸承的剛度呈周期性變化，而軸承剛度變化引起了軸承的振動。

3.2 劃傷缺陷軸承振動仿真結果

令劃傷缺陷的寬度為0.8 mm，深度為0.1 mm，初始方位角為0°。本研究分別設劃傷缺陷位于外圈滾道和內圈滾道，利用Simulink進行仿真求解，得到軸承外圈向振動加速度信號隨時間的變化，如圖7所示。

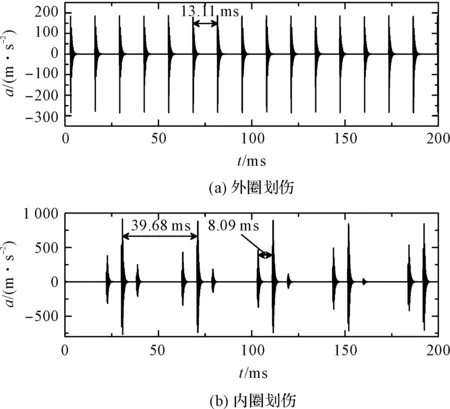
圖7 劃傷缺陷軸承振動響應(a外圈劃傷b內圈劃傷)

對應的包絡譜如圖8所示。

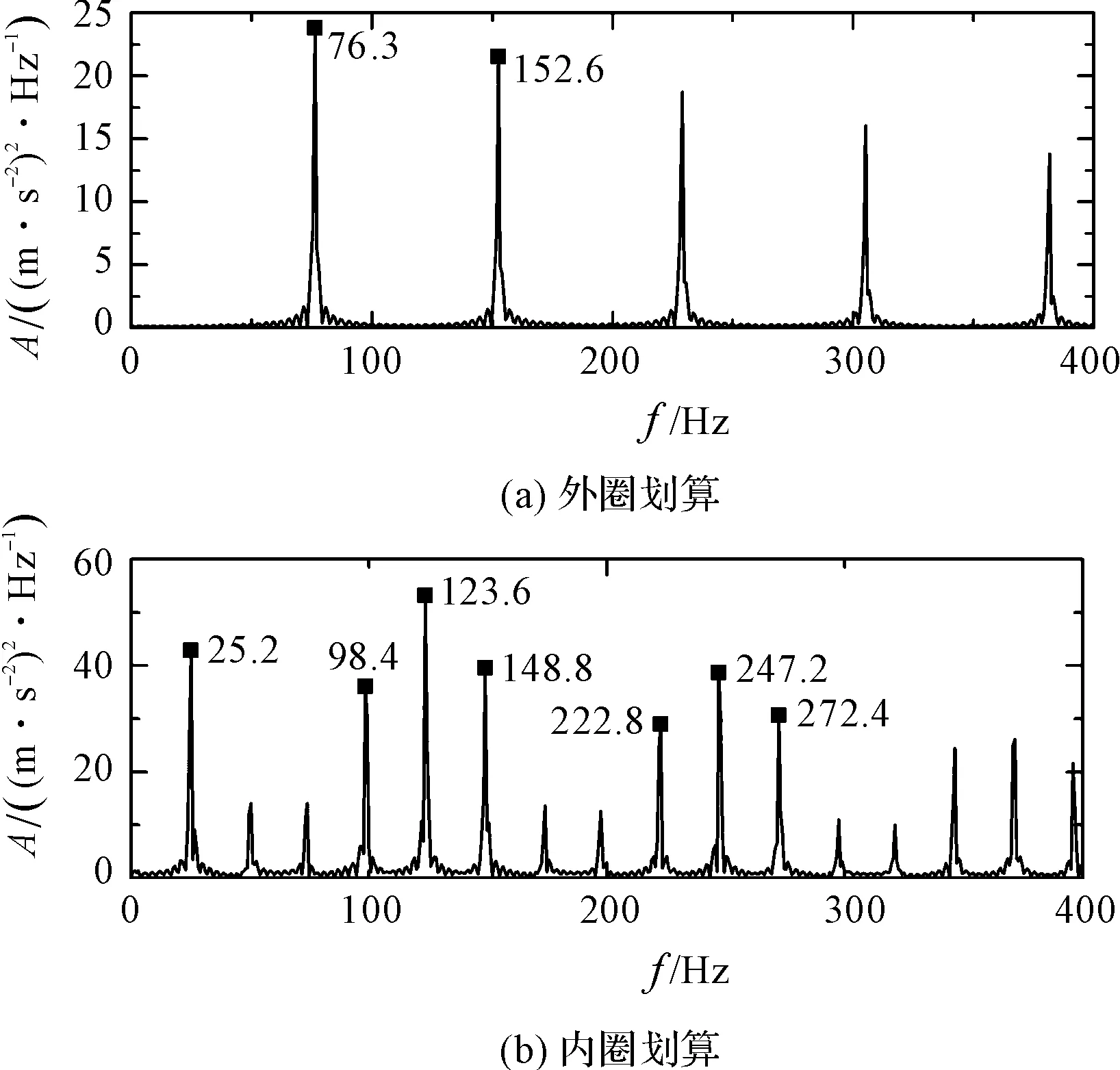
圖8 劃傷缺陷軸承振動包絡譜(a外圈劃傷b內圈劃傷)

由圖(7，8)可以看出：

(1)軸承劃傷缺陷激起了軸承的高頻固有振動，表現為軸承外圈振動信號中周期性的阻尼振蕩衰減波，如本例中外圈劃傷和內圈劃傷引起的振動衰減波周期分別為13.11 ms和8.09 ms；

(2)產生的阻尼振蕩衰減波出現的頻率與鋼球通過缺陷的頻率有關，即特征缺陷頻率，通過對振動信號進行包絡分析可以有效地提取特征缺陷頻率，可以看到軸承缺陷頻率及其倍頻的存在，即外圈缺陷頻率為76.3 Hz，內圈缺陷頻率為123.6 Hz，這與理論結果一致；

(3)外圈劃傷缺陷產生的阻尼振蕩衰減波幅值基本相等，而內圈劃傷缺陷產生的阻尼振蕩衰減波幅值受到了調制，調制波的周期為39.68 ms，頻率為25.2 Hz，即為內圈的轉動頻率；這在圖8包絡譜分析中表現為在內圈劃傷缺陷頻率附近存在旁瓣頻率成分，間隔為內圈轉動頻率25.2 Hz，該現象與文獻[1]給出的結果一致。

3.3 動力學模型驗證

基于BVT-5型軸承振動測量儀，筆者分別使用含有內圈劃傷、外圈劃傷缺陷的滾動軸承進行振動測試。當施加徑向載荷為1 000 N，主軸轉速為1 500 r/min時，采集軸承外圈徑向振動信號，并對其進行包絡分析。本研究將實驗結果和仿真結果作對比，如圖9所示。

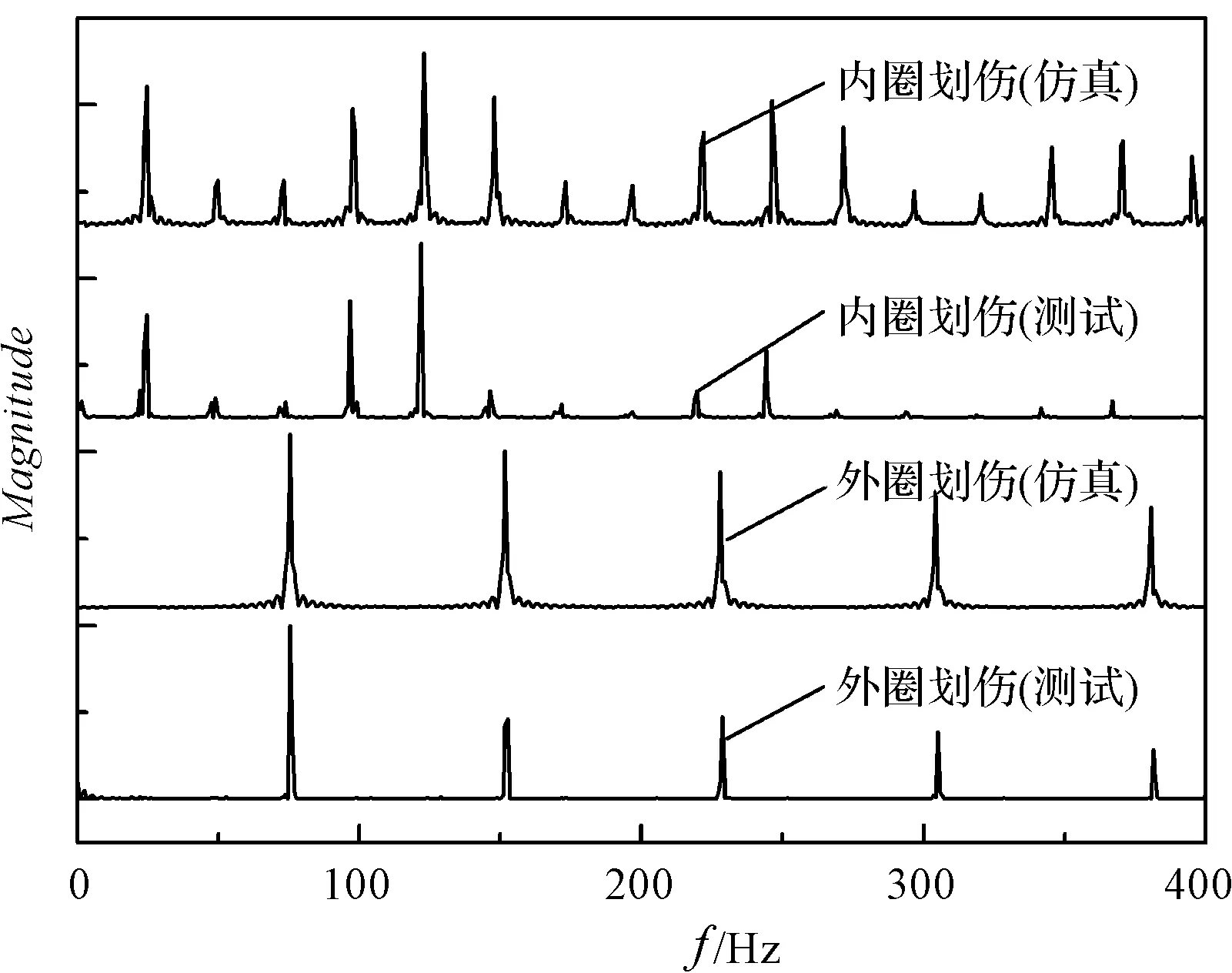
圖9 動力學模型的驗證

其中，本研究對振動包絡譜幅值經過了歸一化處理。由對比結果可以看出：劃傷缺陷軸承振動的仿真結果與實測結果基本一致，都存在劃傷缺陷頻率及其倍頻成分。因此，本文給出的基于Simulink的滾動軸承動力學分析結果是正確的。

4 結束語

基于接觸力學方法，本文通過將額外彈性趨近量引入到缺陷激勵模型中，建立了滾動軸承劃傷缺陷的非線性動力學模型，并基于Matlab/Simulink對模型進行仿真求解，得到了接觸變形、接觸載荷及外圈加速度隨時間的變化結果。

根據仿真結果，本文對缺陷軸承的振動特性進行了分析。研究結果表明：徑向載荷作用下，正常軸承內圈-外圈接觸變形量和接觸載荷均呈周期性變化，導致軸承剛度呈周期性變化，因而軸承外圈Z向仍存在周期性的低幅振動；劃傷缺陷激起軸承的高頻固有振動，產生周期性的阻尼振蕩衰減波，其出現的頻率為特征缺陷頻率；外圈缺陷引起的阻尼衰減波幅值基本相等，而內圈缺陷引起的阻尼衰減波幅值受到了調制。同時，根據劃傷缺陷引起的振動響應包絡譜的實驗結果與仿真結果的對比，驗證了動力學模型及Simulink仿真模型的正確性。

參考文獻(References):

[1] TANDON N， CHOUDHURY A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings[J].TribologyInternational，1999，32(8):469-480.

[2] MCFADDEN P D， SMITH J D. The vibration produced by multiple point defects in a rolling element bearing[J].JournalofSoundandVibration，1985，98(2):263-273.

[3] MCFADDEN P D， SMITH J D. Model for the vibration produced by a single point defect in a rolling element bearing[J].JournalofSoundandVibration，1984，96(1):69-82.

[4] CHOUDHURY A， TANDON N. Vibration response of rolling element bearings in a rotor bearing system to a local defect under radial load[J].JournalofTribology，2006，128(2):252-261.

[5] 陳於學，王冠兵，楊曙年. 滾動軸承早期缺陷振動的簡化模型[J]. 軸承，2007(10):18-21，34.

[6] 曹宏瑞，李亞敏，成 瑋，等. 局部損傷滾動軸承建模與轉子系統振動仿真[J]. 振動、測試與診斷，2014，34(3):549-552.

[7] 伍濟鋼，楊曾增，蔣 勉，等. 滾動軸承表面損傷故障動力學建模方法研究[J]. 機械傳動，2016(2):27-33.

[8] ARSLAN H， AKTURK N. An investigation of rolling element vibrations caused by local defects[J].JournalofTribology，2008，130(4):41101.

[9] PATEL V N， TANDON N， PANDEY R K. A dynamic model for vibration studies of deep groove ball bearings considering single and multiple defects in races[J].JournalofTribology，2010，132(4):41101.

[10] AHMADI A M, PETERSEN D， HOWARD C. A nonlinear dynamic vibration model of defective bearings-the importance of modelling the finite size of rolling elements[J].MechanicalSystemsandSignalProcessing，2015，52-53(1):309-326.

[11] PATEL V N， TANDON N， PANDEY R K. Vibration studies of dynamically loaded deep groove ball bearings in presence of local defects on races[J].ProcediaEngineering，2013( 64):1582-1591.

[12] HARRIS T A， KOTZALAS M N. Rolling bearing analysis[M]. New York: Wiley，2001.

[13] 孔佳元，張 雷.考慮柔性和間隙的螺旋引緯機構仿真分析[J].輕工機械，2017，35(1)：5-9.

[14] 徐國寶，馬金鳳，王延軍.基于Adams的跌落式裝箱機動力學仿真研究[J].包裝與食品機械，2016(1)：44-47.