遺傳算法在物流配送線路選擇方面研究

1 概述

物流配送路徑最短問題是典型的旅行商（Traveling Salesman Problem，TSP）問題。車輛從配送中心出發，將車上貨物分別送到本轄區內的其它分發點（簡稱節點）1,2,3,…,n，車輛在一次配送任務中，只經過各節點一次。由于交通管制和道路方面的原因，可能存在各節點間并不完全互通，個別節點間可能還存在單向性通行，如圖1物流配送路線示意圖。

對于這樣一個典型的TSP問題，隨著節點數目的增加，其可能的配送路線數目與節點數目n是成指數型增長的，是一個NP難題，所以很難精確的求出其最優解，因此尋找有效的近似求解算法就具有重要的現實意義。遺傳算法是一種仿生算法，核心思想起源于對生物進化過程的認識。通過模仿生物的進化，利用達爾文的進化論和孟德爾遺傳變異思想對研究問題進行數學抽象和建模。

遺傳算法是通過模仿生物的繁殖、基因變異、物種間競爭和自然選擇對研究問題采取適當的計算策略，最終得到研究問題的滿意解。遺傳算法只利用研究問題的目標滿意度評價信息，是一種多條并行的隨機搜索優化方法，適用于大規模、高度非線性以及無解析表達式的問題，有很強的通用性[1]。物流配送的路線最短選擇問題采用該方法非常合適。

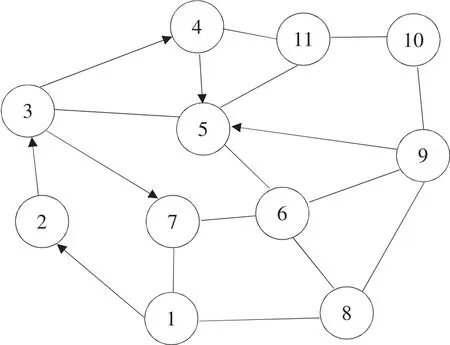
圖1 物流配送路線示意圖

2 數學建模及求解方法

（1）路線信息。對于從物流配送中心出發，將貨物分別投送至各分發點的配送路線之間的關系，可以用表1物流配送節點信息表進行表達（假定11個節點）。對于路線的單向性或節點彼此不通的路線，設值一個比正常路徑大幾個數量級的值，如表1中設定1 000。對各分發點進行節點編號。表1中列表示出發，行表示到達，如：第2列第3行取值為3，表示從節點2出發，到達3節點路程為3個單位。

（2）創建初始種群。對于物流配送車輛所經過的各節點編號所構成的一條路線為一個個體（稱染色體），節點編號在個體中稱基因。基因在個體中的位置不同，個體的表現（路程大小）不同。為了增加個體進化效率和多樣性，初始個體數量一般選擇得都比較多，這些初始個體所構成的集合稱為初始種群。對于本問題，選擇初始種群的規模為100個。初始種群可借由MATLAB的randperm函數產生。由randperm函數按照分發點的節點編號所產生的一個個體形如：5 11 4 8 10 9 2 6 1 7 3。個體中節點編號是隨機排列的，每次調用randperm函數所生產的個體都可能互不相同。

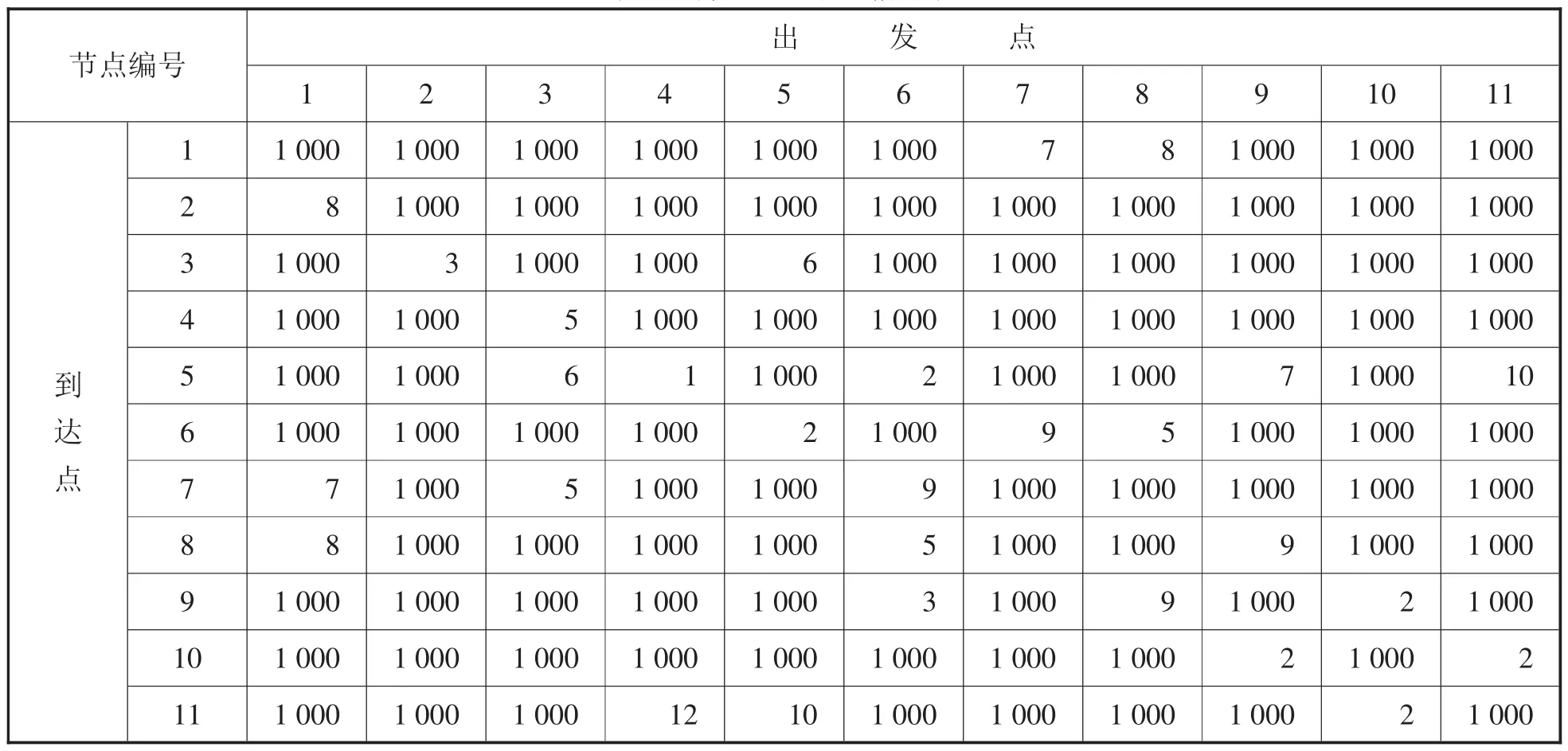
表1 物流配送節點信息表

（3）個體評價和選擇。對于創建的初始種群需要對每個個體進行評價，好的個體和差的個體應當通過適當規則進行保留和淘汰。依據節點信息（表1）對創建的初始種群中每個個體按節點編號順序所構成的路線的路程值大小作為個體的適應度評估函數，越小表明個體的適應度越好，反之越差。在個體保留和淘汰方法上有多種策略，最常見的有輪盤賭法、隨機聯賽法、無回放余數比例隨機法等，本文選擇隨機聯賽法。隨機聯賽法是隨機抽取種群中兩個個體，比較其路程值，路程小的個體被保留，路程大的個體被淘汰。選擇后的種群規模和選擇前的種群規模保持相同。

（4）染色體編碼。遺傳算法運行過程不對所求解問題的實際決策變量直接操作，而是對表示可行解的個體的編碼進行交叉和變異操作。編碼就是把一個問題的可行解從其解空間轉換到遺傳算法所能處理的搜索空間的轉換方法[1]。對物料配送路線的編碼方法比較多，本文選取Grefenstette等提出的編碼方法。對上述個體5 11 4 8 10 9 2 6 1 7 3采用Grefenstette編碼方法得到的染色體為：5 10 4 6 7 6 2 3 1 2 1。

（5）染色體交叉。染色體交叉是將種群中的染色體（種群中的個體）按照交叉概率，隨機選取染色體，隨機對染色體基因位置之前或之后的基因進行互換操作。本文采用隨機交叉點之前的基因對隨機選取的兩條染色體進行交叉操作。

（6）基因變異。基因變異是將對構成染色體的基因，按照變異概率，隨機選擇染色體上的基因進行隨機改變的操作。由于染色體的編碼方法決定了不同位置基因的可能取值，因此基因變異后，在該位置上的基因值應保證是有效的基因改變。

（7）解碼和新個體評價。在染色體交叉、變異完成后，得到下一代新的種群。為了評價新種群中個體（染色體）的優劣，需要首先將編碼的染色體按編碼的逆過程進行解碼。對解碼后的染色體按照適應度進行評估，并按上述所確定的個體選擇規則保留或淘汰。

（8）計算進化代數和差異。計算種群中適應度最好的個體，即路程最短的個體，并將該個體與上一代表現最好的個體進行對比，計算他們之間的差異值；同時計算種群進化的代數，當兩條件都達到程序結束運行條件時程序就停止計算，并將優化結果輸出。

3 求解及結果分析

按照遺傳算法的計算策略，采用MATLAB編制的求解程序框圖如圖2所示。

經過幾次運行其計算結果如下：

進化第116代，當前最小值61.000，共有1個最小值解；

群體中第64個個體，最小值61.000，2→3→4→5→11→10→9→8→6→7→1；

進化第385代，當前最小值61.000，共有51個最小值解；

群體中第2個個體，最小值61.000，11→10→9→8→6→7→1→2→3→4→5。

從優化計算的結果看，雖然得到最優解的進化代數各不相同，但都能得到相同的結果。上述求解得到的路線2→3→4→5→11→10→9→8→6→7→1與路線 11→10→9→8→6→7→1→2→3→4→5在形式上不完全相同，但所確定的路線是完全一致的。結果表明，從配送中心出發，遍歷各分發點的最優路線為：1→2→3→4→5→11→10→9→8→6→7，總路程為61個單位。

4 結論

采用遺傳算法求解物流配送路線最優選擇是可行有效的方法。遺傳算法只與求解問題的目標函數取值信息有關，而與實際所研究問題的類型和數學特性無關，因此具有廣泛的普適性。對于多節點遍歷問題或多孔加工路線最優選擇等實際問題都可以利用遺傳算法進行求解。

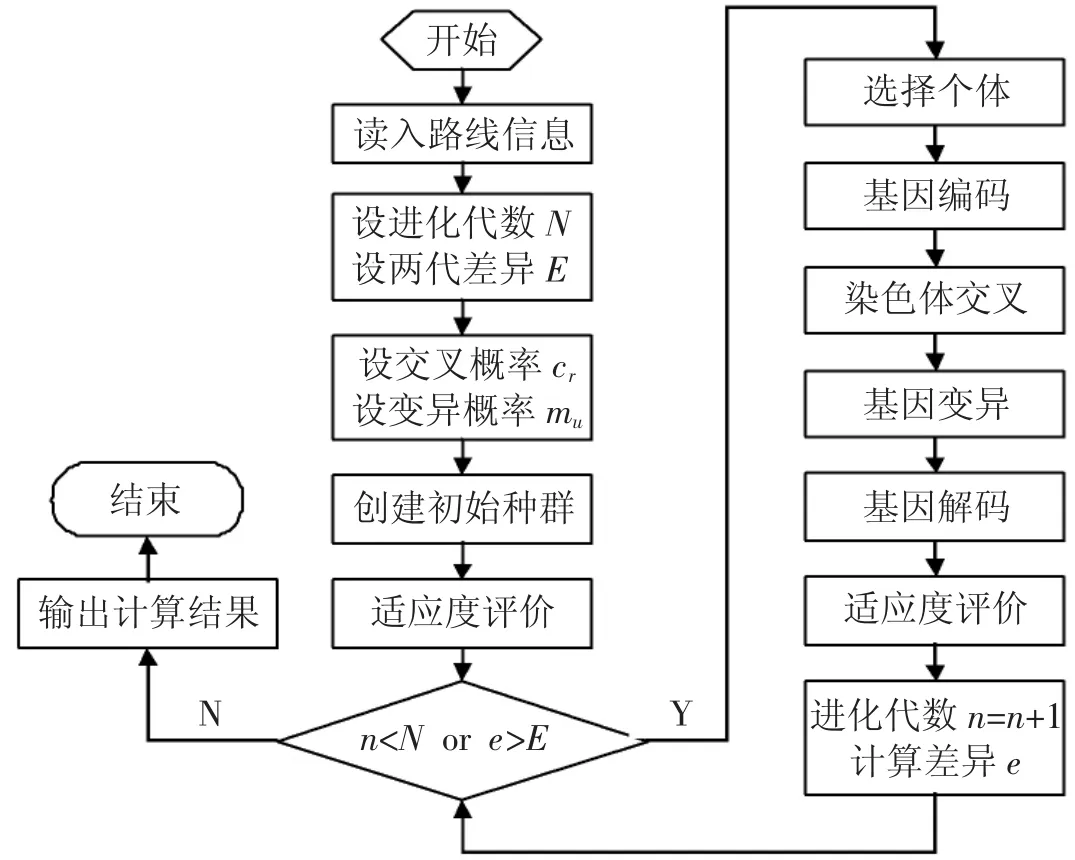
圖2 遺傳算法求解物流配送路徑最短流程圖

參考文獻：

[1]周明，孫樹棟.遺傳算法原理與應用[M].北京：國防工業出版社，1999:143-157.