高超聲速飛行器時間協同再入制導

方科，張慶振，倪昆，程林，黃云濤

1.北京航空航天大學 自動化科學與電氣工程學院，北京 100083 2. 北京航天自動控制研究所，北京 100076

以無動力高超聲速再入飛行器為代表的遠程作戰武器具有作戰范圍廣、飛行速度快、跟蹤難度大、作戰效能高等特點[1]，在近些年來受到各國越來越多的關注。與此同時，各國相繼研發了近迫武器系統(CIWS)、“宙斯盾”等一系列反導系統[2]，使得其作戰效能與突防能力大幅下降。在此背景下，相對于傳統提高單兵作戰效能的方法，發展多飛行器協同飽和打擊更加符合未來戰場作戰需要，其個體之間通過功能互補可以實現飽和攻擊、協同抗干擾等復雜功能。

高超聲速飛行器的遠距離飛行和復雜不確定性環境特點，使得飛行時間具有較大波動，難以實現在同一時刻對目標進行飽和打擊的任務需求。其中再入飛行段占據了90%以上的飛行時間，是決定最終飽和打擊效果的關鍵因素之一。因而發展多高超聲速飛行器協同再入制導技術是未來協同體系作戰的必要條件之一。

本文以多高超聲速飛行器協同飽和打擊為應用背景[3-5]，將其飛行過程分為初始發射段、協同再入段和協同末制導段。其中初始發射段通過程序發射序列確保協同再入的可行性；協同末制導段由文獻[5-9]實現。而在這之間的協同再入段占據了整個飛行過程中的絕大多數時間與路程，在傳統單飛行器高精度、高可靠性的再入制導律基礎上，要求多飛行器能在同一時刻到達指定的中末交班地點。協同再入飛行[3,10]作為近兩年來的新型任務需求，針對其協同制導結構與制導律的設計，現有文獻均鮮有涉及。

單個高超聲速飛行器的再入制導是一個復雜的多約束軌跡規劃問題，現階段主要有“標稱軌跡法”和“預測-校正法”[11-14]。前者離線生成標準彈道并在實際再入過程中進行軌跡跟蹤，簡單易行但自主性和精度較差。后者在彈道預測的基礎上進行軌跡校正，自主性與精度較高，但實時性較差且在線約束管理能力較弱[11-12]。

多彈協同制導技術不同于多無人機[15-16]和多機器人[17-18]的協同控制，其運動速度快、運動方向單一、能量耗散過程不可逆等特點[6,19]使得多無人機的協同控制方法無法直接使用。林濤等[19]首先對多彈協同的基本問題進行闡述；2006年，Jeon等[5]實現指定飛行時間的最優末導引律設計。趙世鈺和周銳[6-7]結合協調變量[8]提出雙層協同制導架構；2009年，張友安等[9]提出“領彈-從彈”的協同制導架構。后續的研究工作大部分是針對這兩套架構的拓展與完善，并且主要集中于末制導律的設計上。

高超聲速飛行器時間協同再入制導將以上兩個技術相結合的同時，也催生出其特有的難點：

1) 時間協同再入飛行對再入制導律的實時性、在線約束管理等方面提出更高的要求，需要對現有方法加以優化。

2) 現有再入制導律并沒有考慮飛行時間約束，飛行過程中的參數攝動使得再入時間不可知且不可控，難以滿足協同再入飛行的時間一致性要求。因而需要將時間約束加入到制導律的設計之中，解決再入時間的不可預知性和不可控性。

3) 高超聲速飛行器相對于傳統導彈，其飛行速度更快、再入過程更為復雜、控制變量較為單一，并且無動力的再入飛行特點使得總能量有限且控制過程不可逆，無法直接將例如文獻[6]中的雙層協同結構運用于協同再入制導中，因而需要在協同結構和協調策略上進行改進和創新。

本文首先對現有單個飛行器的制導律加以改進，提升其實時性、在線約束管理能力以滿足協同再入制導任務需要；進而針對再入飛行時間可知性與可控性問題，提出時間可控再入制導律；最后根據協同再入任務背景需求，基于多飛行器時間協調信息提出協同再入制導結構和協調策略，實現多高超聲速飛行器的時間協同再入飛行過程。

1 協同再入問題描述

在不考慮地球自轉的情況下，多個無動力高超聲速飛行器三自由度運動方程為

(1)

式中：下標i代表第i個飛行器；v為其相對于地球的速度；r為飛行器到地球中心的距離；λ和φ為地球經緯度；Se為射程角；θ為速度傾角，向上為正；ψ為速度偏航角，以正北順時針為正；σ為傾側角，右偏為正；m為飛行器質量；g為地球重力加速度；L和D為升力和阻力。

(2)

(3)

(4)

(5)

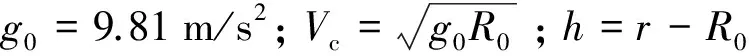
再入過程中終端約束與控制約束如式(6)～式(8)所示:

h(tf,i)=hf,i，v(tf,i)=vf,i

(6)

λ(tf,i)=λf,i，φ(tf,i)=φf,i

(7)

(8)

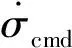
針對終端時刻一致的協同再入過程，給出整個飛行過程的時間約束如式(9)所示:

tf，1=tf，2=…=tf, n

(9)

式中：tf,i為第i個飛行器的終端時刻。

仿真對象為CAV-H，相關參數詳見文獻[20-21]。由文獻[20]可知再入過程中采用的固定攻角剖面為

(10)

2 協同結構與制導方案

2.1 協同結構

多高超聲速飛行器協同再入的核心任務是在同一時刻到達指定交班點。結合文獻[6]與協同再入背景，設計協同再入制導架構如圖1所示。其中再入過程分為初始下滑段、平衡滑翔段和再入終段[14]。

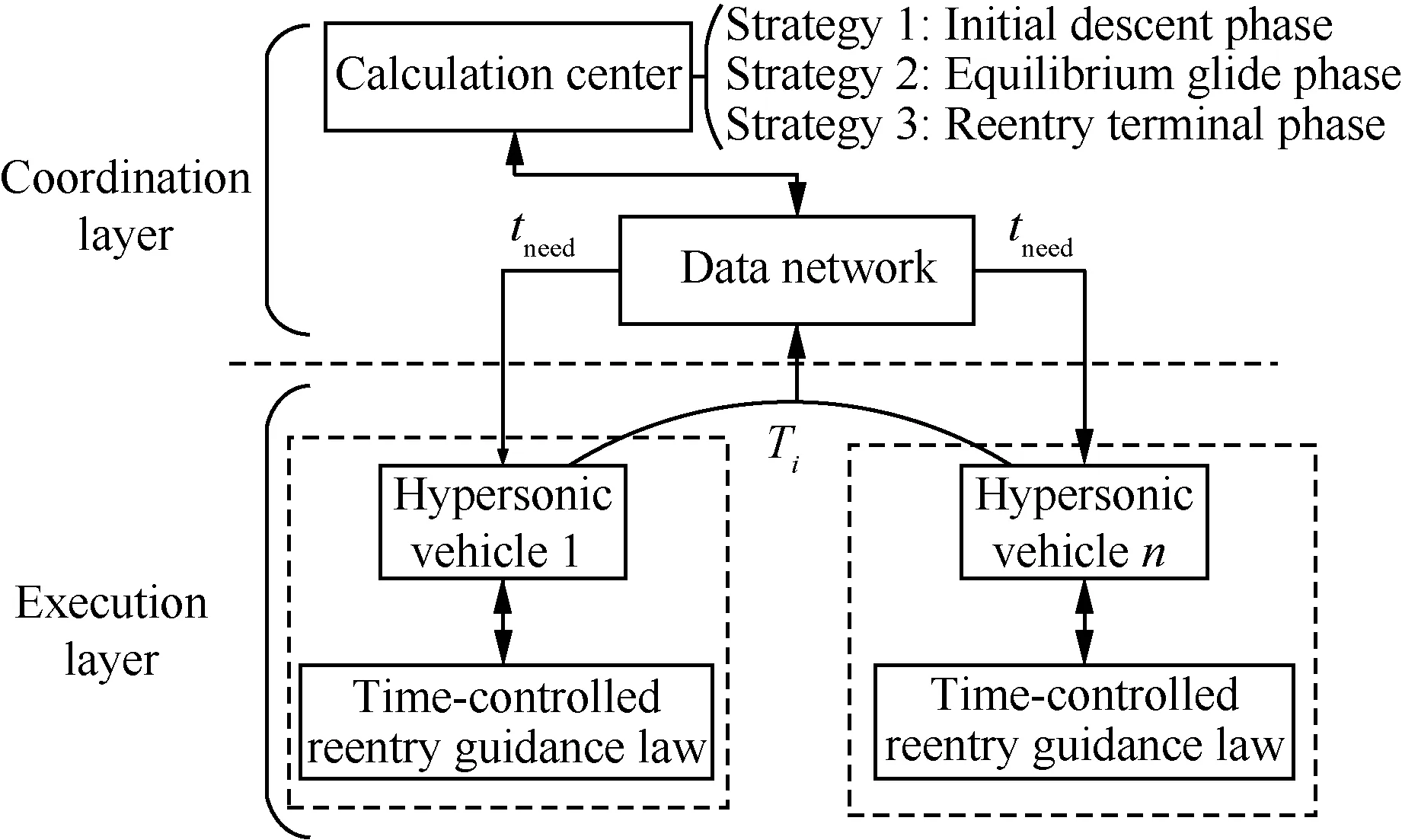
圖1 協同再入制導架構Fig.1 Architecture of cooperative reentry guidance

整個協同結構分為兩層，上層為協調層，適用于分布式/集中式的通訊結構，生成時間協調信息[8]；下層為執行層，由時間可控再入制導律進行在線軌跡預測與校正。

本文以集中式的通訊結構為例進行相關結構的設計。多個飛行器通過中繼衛星等外部設備，將各自的預估飛行時間Ti傳給集中運算單元。運算單元根據協調策略計算時間協調信息tneed，并將其傳回至各飛行器，各飛行器以時間協調信息為約束進行在線軌跡設計。不同再入飛行階段的協調策略各不相同，具體見本文3.3.3節。

2.2 時間可控再入制導方案

時間可控再入制導總體方案如圖2所示,主要包括軌跡預測-校正、在線約束管理和再入飛行時間預估-校正3個模塊。圖中：α為功角；σd為軌跡規劃模塊求得的傾側角;σcmd為指定的傾側角。

圖2 總體制導方案Fig.2 Overall scheme of reentry guidance

首先,軌跡預測與校正模塊在理論推導的基礎上進行控制剖面參數化，在滿足約束的前提下將原本復雜的軌跡規劃問題轉換為單參數的規劃，通過在線傾側角剖面調整信息的收集與預測，利用一次軌跡積分完成傾側角剖面的調整，減少制導周期內的冗余計算并提高實時性。其次,在線約束強化管理模塊引入控制理論的相關方法，實現對過程約束、終端約束和控制約束的在線強化管理，在不需要前期大量參數試湊的前提下提高制導律的在線約束管理能力。最后，時間預估-校正模塊在時間敏感性分析的基礎上，將視線角走廊作為控制變量，采用神經網絡和Gauss-Newton迭代法實現基于時間誤差的視線角走廊動態調整策略，實現指定時間的再入飛行。

3 時間可控再入制導律

3.1 軌跡預測-校正

3.1.1 控制剖面參數化

再入過程是一個復雜的多約束規劃問題，傳統方法通過人為設定規劃點以達到在線求解的目的，限制了飛行器的能力，難以滿足協同再入任務自主性要求，因而需要進行改進。首先構建圖 3所示的高度-速度(H-V)走廊和如圖 4所示的復合傾側角走廊，具體流程見文獻[11]。

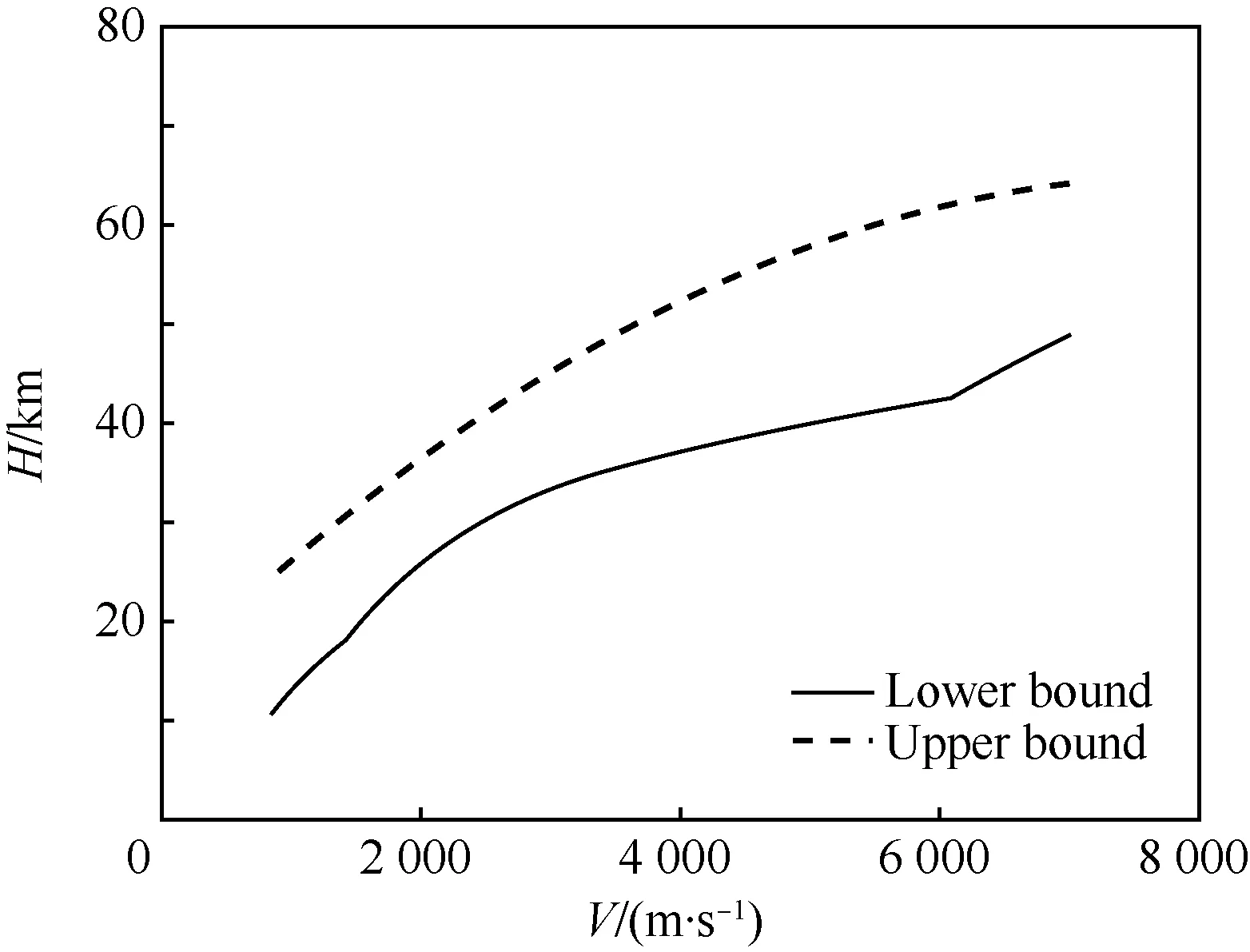
圖3 高度-速度走廊Fig.3 Altitude-velocity corridor

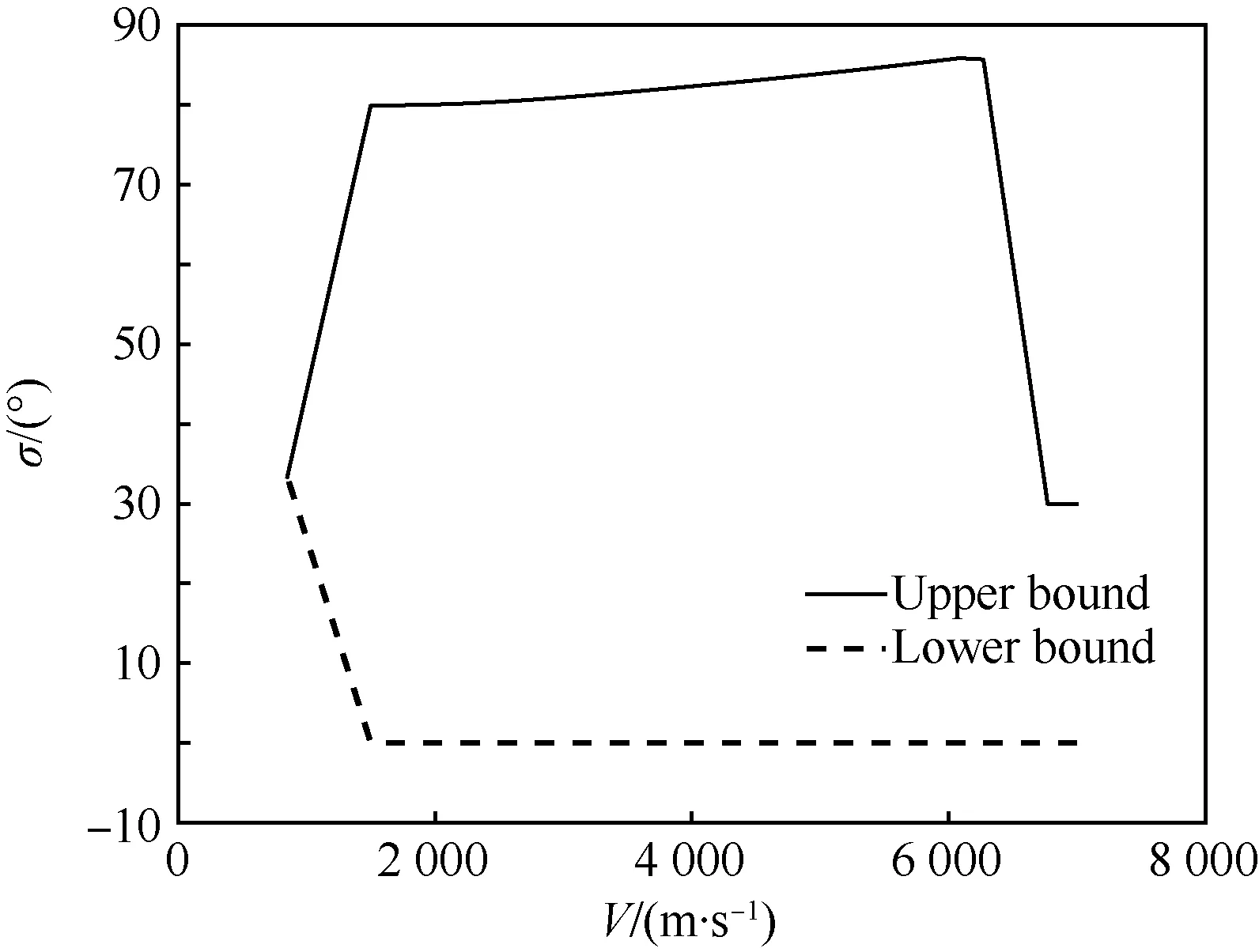
圖4 復合傾側角走廊Fig.4 Compound bank angle corridor

終端經緯度約束可轉化為如式(11)所示的射程約束：

(11)

將式(1)中的射程角對速度求導可得

(12)

式中：CD為阻力系數；Sref為參考氣動面積。

聯立式(11)和式(12)可以定性的得出以下結論：一定速度下，|dSe/dv|關于高度h的增加而單調遞減；結合擬平衡滑翔假設[11]可進一步得到推論，隨著傾側角的增大，|dSe/dv|增大，飛行器滑翔能力和飛行距離減小；反而反之[14]。

再入軌跡規劃本質上是多約束條件下的非線性規劃問題。在上述推導的基礎上進行控制剖面參數化，將傾側角走廊上下界進行加權得到規劃的傾側角剖面。

σd(v)=ωσmin(v)+(1-ω)σmax(v)

(13)

式中：σd(v)為某速度下規劃的傾側角；σmin(v)和σmax(v)分別為某速度下傾側角走廊上下界；ω為權重系數。不同權重下的射程規劃能力如圖 5所示。

通過控制剖面參數化，在滿足過程約束、終端約束的基礎上，將再入過程中的射程約束轉化為權重系數ω的單參數規劃問題，并且二者呈如圖5所示的單調遞增關系，降低了問題求解難度和提高了射程規劃能力。

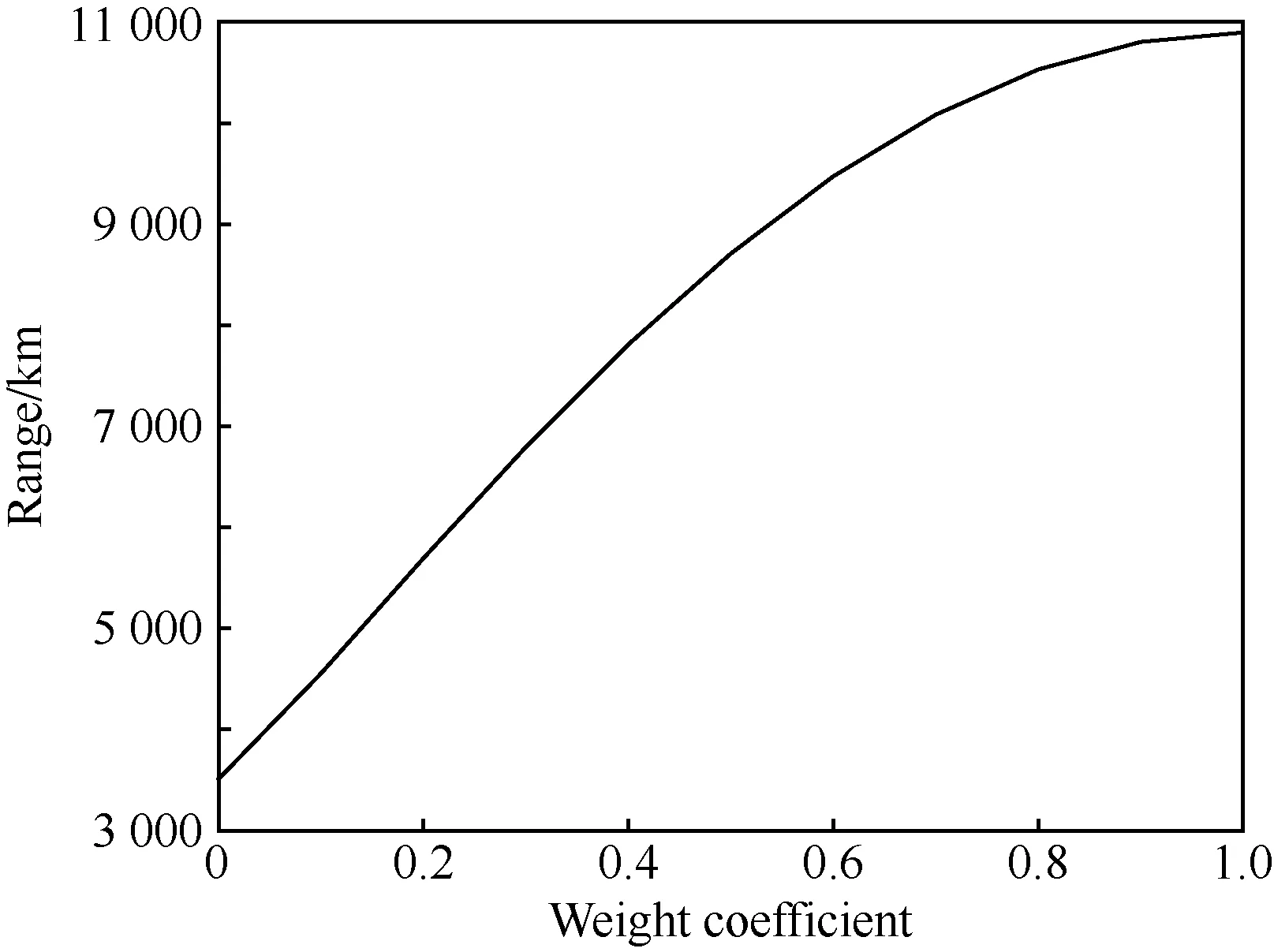
圖5 權重系數-射程Fig.5 Weight coefficient-range

3.1.2 跨周期軌跡預測-校正

傳統預測-校正制導方法在每個周期內通過多次的軌跡積分來獲取必要的參數調整信息，造成大量冗余計算和規劃周期不穩定情況出現[14]，難以滿足協同再入要求。由于多個制導周期之間的控制剖面調整信息存在一定的連續遞推關系，因而采用校正信息在線收集與預測方法，將這部分遞推信息進行有效的收集與模型辨識。由圖 5的單調性可知，規劃射程與權重系數可在小范圍內近似成式(14)的一階線性函數關系:

Spre(ω)≈aω+b

(14)

式中：Spre為規劃射程；a、b為待估計參數。通過前k個周期的剖面調整收集，得到的觀測模型為

Hkx+Ek=Zk

(15)

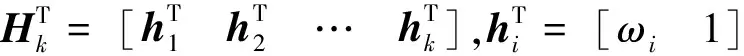
為達到最優的參數估計結果，最小化式(16)性能評價指標:

(16)

式中：正定陣Qk為權重矩陣。利用前k個周期的剖面調整與預測信息，對第k+1個周期的權重系數進行估計，其中加權矩陣迭代設置為

(17)

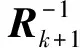
最終估計參數表達式為

(18)

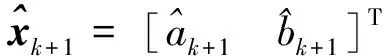
(19)

通過式(18)和式(19)，將原本隱函數關系的權重-射程函數式(14)進行了顯式的遞推表達。因而在整個制導過程中，利用式(19)對前k個周期剖面調整與預測信息的觀測，遞推出如式(18)所示的第k+1個周期的估計參數，進而直接求解出第k+1個周期的剖面調整信息，即

零工經濟(Gig Economy)中的零工(Gig)原意是指臨時工，是一些勞動者無法獲得正式工作，只能從事一些臨時性工作[1]。由于產業的周期性以及季節的周期性，有些工作并長期不雇傭勞動力，往往是需要的時候才雇傭工人，此時就會出現大量勞動力以團隊形式暫時的集聚于某一地方或某一產業的現象，例如農民工[2,3]。由這種臨時工所形成的經濟現象被稱為零工經濟。改革開放以來，我國的很多城市中都出現過這種“零工”現象。

Spre(ω)=Sgo

(20)

(21)

式中：Sgo為所需的剩余射程。

通過在線的參數收集與遞推，在每個制導周期內僅需要一次軌跡積分即可完成傾側角剖面的調整，大大提高了在線軌跡規劃效率，滿足協同再入制導的在線軌跡規劃實時性要求。

3.2 在線約束強化管理

軌跡預測-校正為再入過程提供可行的縱向軌跡，但實際飛行中再入軌跡仍然存在違反約束的情況[11,14]，因而需要對其進行在線約束強化管理，提高制導律的可靠性與穩定性。具體流程如圖6所示，其中約束管理對象包括過程約束、終端約束和控制約束。圖中：σco為修正的傾側角指令；σpo為濾波前的傾側角指令。

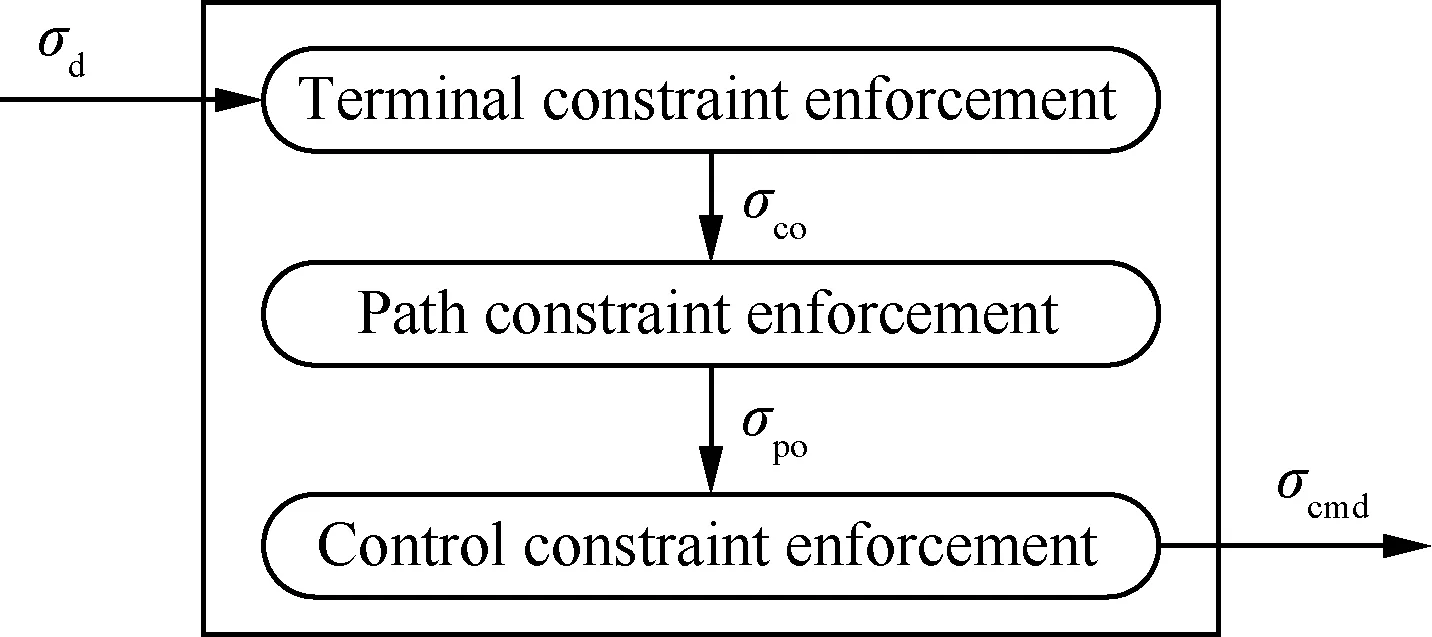
圖6 在線約束管理Fig.6 Online constraint management

3.2.1 過程約束管理

由式(2)～式(4)可知，再入過程中的熱流、動壓、過載約束可以轉化為H-V走廊下界，并且存在唯一的高度-速度對應關系。引入剩余高度:

Δhd=h-hdown>0

(22)

式中：hdown為當前速度下H-V走廊下界高度。

為保證飛行高度總是在走廊下界之上，對高度求導并設計如式(23)所示的高度下降速率限制器為

(23)

式中：λh為高度趨近系數。

當飛行器存在超過下界趨勢時，該模塊將傾側角限制到合理的范圍之內，而這其中產生的射程誤差又能在后續的制導周期中得到補償，因而不會影響整個再入過程的精度。同時，其計算量極小且校正過程基于當前高度信息因而不需要前期的參數試湊，具有較高的約束管理可靠性。

3.2.2 終端約束管理

再入過程還需要滿足如式(6)的終端高度與速度約束。對式(1)中的高度與速度傾角在擬平衡滑翔條件的平衡點(h,θ)處小擾動線性化可得

(24)

式中：

(25)

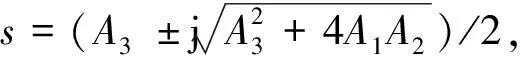
σco=arccos(cosσd+Δcosσ)

(26)

3.2.3 控制約束管理

規劃的傾側角剖面在實際執行過程中受限于式(9)執行速率，需要加入的指令濾波環節為

(27)

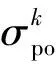
通過以上3種約束強化算法的設計，在不影響實時性的前提下，提高再入制導律的在線約束管理能力，為之后的協同過程提供實時可靠的縱向軌跡支持。

3.3 再入時間預估-校正

3.3.1 視線角走廊設計

一套完整的再入制導律還需要橫向上的傾側角符號規劃。本文在傳統的三段式視線角(Line of Sight，LOS)走廊的基礎上進行時間可控制導律設計。反轉邏輯如式(28)所示，走廊如圖7所示。

(28)

式中：Δψup和Δψdown分別為當前速度下的視線角走廊的上下界。視線角走廊根據CAV-H的再入任務[20]進行設置，v0～v4分別為視線角走廊轉折點速度，初始速度v0=7 000 m/s，初始下滑段走

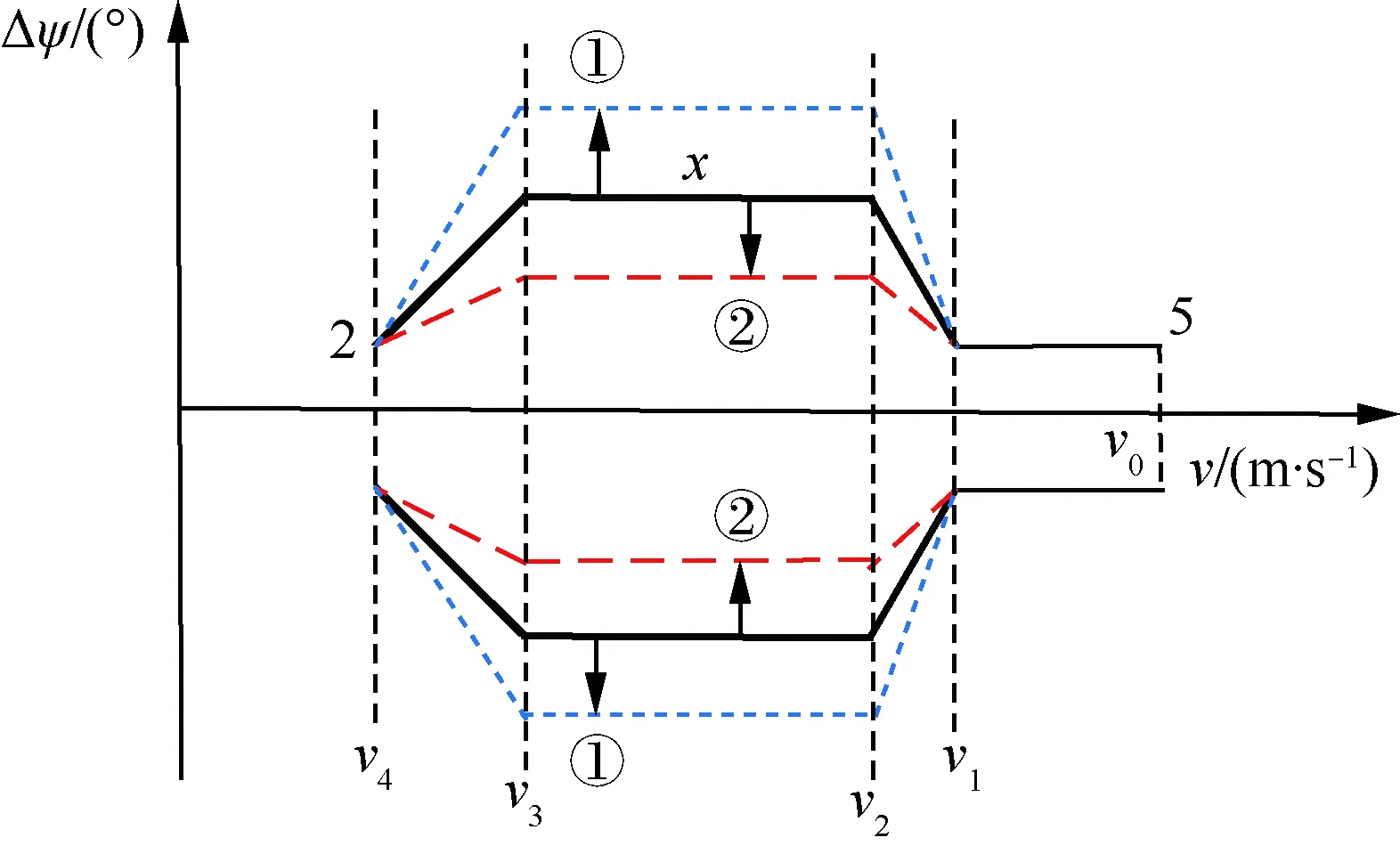
圖7 視線角走廊Fig.7 Line of sight (LOS) corridor

廊上限為5°；終端速度v4=800 m/s，走廊上限為2°；中間段上限為x。

通過對中間段x的調整，可以改變再入過程中橫向移動范圍。當需要增大橫向機動距離時，中間段寬度沿①方向擴大；反之沿②方向收窄。橫向機動距離的改變一定程度上影響再入時間，具體方法見3.3.4節。

3.3.2 再入時間影響因素分析

由于再入過程極為復雜，干擾因素眾多，首先對能夠影響再入飛行時間的因素進行劃分，具體如表1所示。其中，主動因素有攻角剖面的切換速度、最小攻角和視線角走廊的寬度等；被動因素有大氣不確定、初始投放不確定和動態特性(氣動系數、動導數等)不確定等。

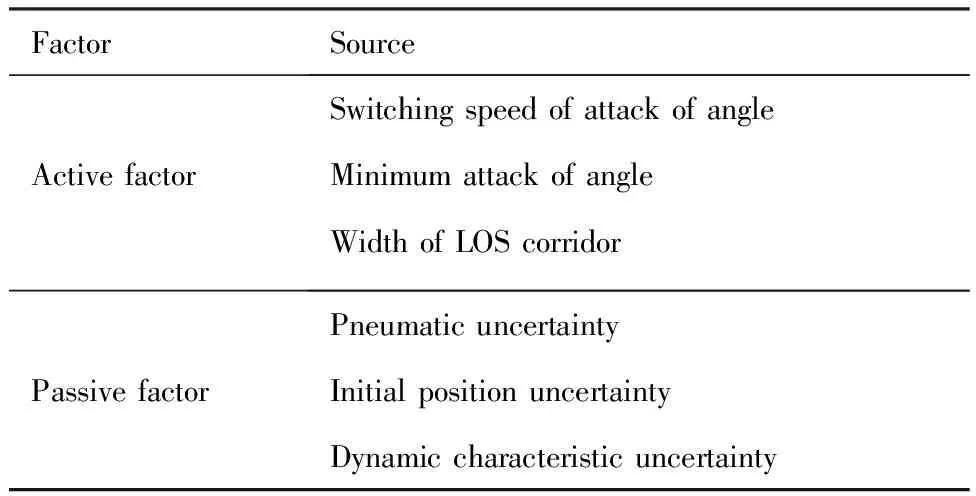
表1 再入時間影響因素Table 1 Influencing factors of reentry time

以標稱環境下飛行時間為1 592 s的再入任務為例，對被動因素進行2 000次蒙特卡羅仿真并統計最終飛行時間誤差，結果如圖 8所示。

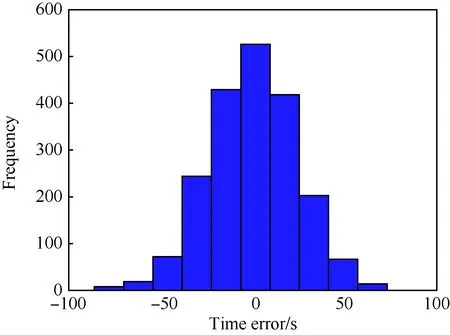
圖8 被動因素產生的時間誤差直方圖Fig.8 Histogram of time errors caused by passive factors

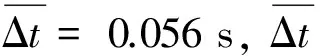
在標稱環境下對主動因素進行調節以研究其時間調整能力，結果如表2所示。其中視線角走廊上界的調節是通過設置圖7視線角走廊的中間段角度x而實現的。

表2 主動因素的影響Table 2 Influence of active factors

由表2可知，通過對主動因素的調整可以實現再入飛行時間的調節，為再入過程的時間調整提供了可行性的基礎。但通過改變攻角剖面進行時間調節的能力有限且能量損耗大。

在傳統多彈協同制導律的設計中，通常在基本導引律之上疊加橫向過載指令，改變橫向機動距離以實現飛行時間的調整[4,7]。高超聲速飛行器的操控能力有限，面對稱的外形無法直接疊加橫向過載，因而最有效地增加橫向機動距離的方法是改變視線角走廊的寬度，表2中的視線角走廊寬度與再入飛行時間的關系如圖9所示。由圖可知，調節視線角走廊寬度可以有效地改變飛行時間且呈單調遞增趨勢，因而在再入過程中采用動態改變視線角走廊寬度的方法以調整再入飛行時間。

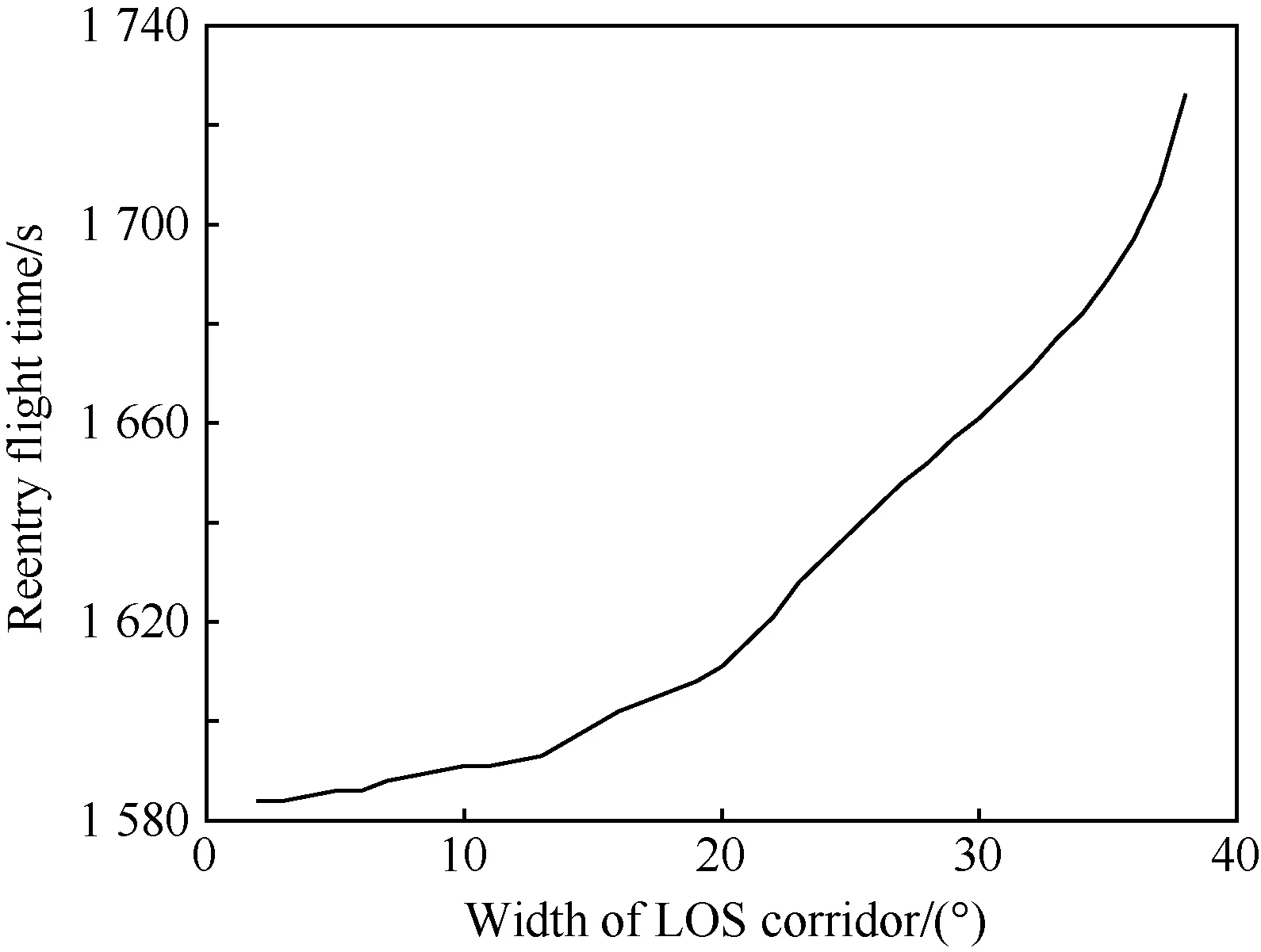
圖9 視線角走廊寬度與再入飛行時間Fig.9 Width of LOS corridor vs reentry flight time

3.3.3 協調信息計算

集群內個體之間的信息共享是實現集群協同運行的基礎，其中所必需的最小量信息被稱之為協調信息或協調變量[6,8]。若每個個體都能接收到相同的協調信息并由此進行動作，則集群的協同運行即可實現。基于協調信息的協同控制作為一種通用方法，為集群協同控制問題提供了一套具有普遍意義的解決方案[6]。

基于協調信息的協同控制方法已成功運用于機器人、無人機等領域之中[7]，因而也為高超聲速飛行器時間協同再入制導提供可能的探索方向。由于協同再入飛行的目的是對目標進行飽和打擊，該過程要求所有飛行器具有相同的再入飛行時間，因而可將其期望值tneed作為協調信息。

若各飛行器再入飛行時間可知且能夠與tneed達成一致，則在多飛行器必然能夠同時完成再入飛行過程。期望再入飛行時間tneed的求取是基于對象特點所設計的協調函數[8]。本文的協調函數具有特殊性，主要由于高超聲速飛行器控制方式單一且控制過程不可逆。前期仿真表明，調整范圍為整個再入時間的4%～5%。以至少需要1 600 s的再入過程為例，可調節的范圍在1 600-1 670 s。其次由于再入過程的復雜性，難以實現文獻[7]中具有明確物理意義且具有次優性的協調信息。因而需要根據不同的飛行階段特點設計相應的協調函數以得到協調信息tneed。

在初始下滑段，飛行器氣動力和機動能力弱，僅需要將運動方向對準目標和保證存在可行的協同再入時間域即可。因而只在初始投放時刻對各飛行器的可行再入飛行時間范圍進行預估并做可協同性分析，即保證多個可行時間域存在重疊，進而求解如式(29)所示的初始可行協調時間:

(29)

式中：tmin,i和tmax,i分別為第i個飛行器的最小和最大飛行時間。在整個初始下滑段中以固定的時間協調信息進行再入軌跡規劃。

在所有飛行器進入平衡滑翔段后，氣動力和機動能力增強，加之長距離的飛行過程使得其有一定的時間調整能力，此時計算中心根據各飛行器預估時間求解時間協調信息，即

(30)

在第m個制導周期，所有飛行器進入再入終段，此時以減小落點誤差和細調再入時間為目標，協調信息沿用第m-1個周期的計算結果:

(31)

3.3.4 時間預估與校正

飛行器再入時間的可知性與可控性是協同制導的基礎，在選定視線角走廊寬度作為時間調整變量和定義協調函數之后，構造如圖10所示的時間可控再入制導系統。

其中時間預估模塊根據當前時刻飛行器狀態對剩余再入飛行時間進行預估，實現再入時間的可知性。進而與期望飛行時間(即協調信息)比較得到時間誤差為

Δtco=tpre-tneed

(32)

式中：tpre為預估剩余飛行時間。偏差量Δtco通過在線的視線角走廊寬度調整得以消除，實現再入飛行時間的可控性。

再入過程是一個復雜的飛行運動學問題，再入時間與諸多因素有關，現階段缺乏有效的方法對其進行分析。通過仿真，在固定視線角走廊下，某次再入過程中的不同參數與再入時間關系如圖11所示。

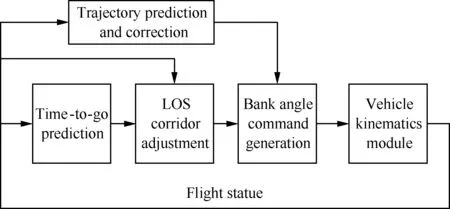
圖10 時間可控再入制導系統Fig.10 Time-controlled reentry guidance system

在加入視線角走廊寬度之后，圖11將更為復雜，本文不再具體展開。基于數值計算的方法很難對如此復雜且連續的函數進行有效的擬合，而神經網絡具有較強的自學習、自適應與非線性映射能力，常被運用于關系復雜的非確定問題研究，因此本文將其用于再入過程中的時間預估。前期仿真與理論分析可知再入時間與飛行器當前的高度、速度、剩余距離、視線角、視線角走廊上界有關，即

(33)

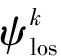
時間預估模塊采用如圖12所示的BP(Back Propagation)神經網絡。在一定大小的訓練數據集(105～106及以上)基礎上，根據Kosmogorov定理，在合理的結構和恰當的權值條件下，3層BP網絡可以逼近任意的連續函數[22-23]。

圖11 不同參數與再入時間的關系Fig.11 Relationship between different parameters and reentry time

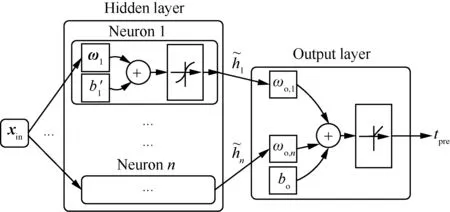
圖12 3層BP神經網絡Fig.12 Three-layer BP neural network

(34)

(35)

輸出層采用斜率為ko(ko>0)的ReLU函數：

G(x)=max(0,kox)

(36)

最終輸出剩余飛行時間預估值為

(37)

1) 標稱環境下，在可達飛行距離范圍內等距離選擇50個經緯度坐標作為仿真的初始投放點，再入任務目標見表 4。

2) 針對每一個再入過程，橫向制導模塊的視線角走廊寬度x以1°為步長由3°變化至28°，重復進行再入軌跡仿真，制導仿真周期為1 s。

3) 記錄整個仿真過程中的5個飛行器狀態量，并由最終的飛行時間倒推出不同狀態量所對應的剩余飛行時間，兩兩結合組成訓練集。

通過以上流程可獲得大小在2×106級別的時間預估網絡訓練集。網絡訓練采用貝葉斯正則化算法以提高其泛化能力和抑制過擬合現象[22]。在每一代的訓練過程中，隨機選擇整個數據集中的85%作訓練集，10%作驗證集，5%作測試集。隱藏層神經元個數的確定采用網格搜索法，在1000代的訓練代數下，網絡效果如圖13，橫坐標nh為隱藏層神經元個數，縱坐標為訓練集和測試集的均方根誤差(Root Mean Square Error，RMSE)

由圖13可知，即使是采用非線性的Sigmoid函數作隱藏層的激活函數，時間預估網絡仍然存在一定誤差，并且與隱藏層神經元個數存在一定的關系。當神經元個數較少時，網絡出現欠擬合；隨著數量的增加，網絡擬合精度逐漸提高，但在超過一定閾值后出現過擬合現象。在多次測試和綜合考慮精度、計算量的基礎上，最終選定的網絡結構為5-20-1。進而對預估模塊實際運行效果進行測試，結果如圖14所示。由圖可知即使在加入參數拉偏后，整個再入過程中的時間預估誤差仍在±7 s以內。其中由于在初始下滑段和再入終段，視線角走廊存在拐點，從而造成較大的估計誤差，但不影響總體的時間預估效果。

橫向走廊的寬度直接影響了再入過程的橫向機動范圍，調節橫向機動范圍可以對再入飛行時間進行調整，并且存在如圖9的連續單調遞增關系。以圖7為例，具體的走廊調整策略如下：

1) 初始下滑段氣動能力較弱，需要飛行器對準目標方向，不進行走廊的調整。

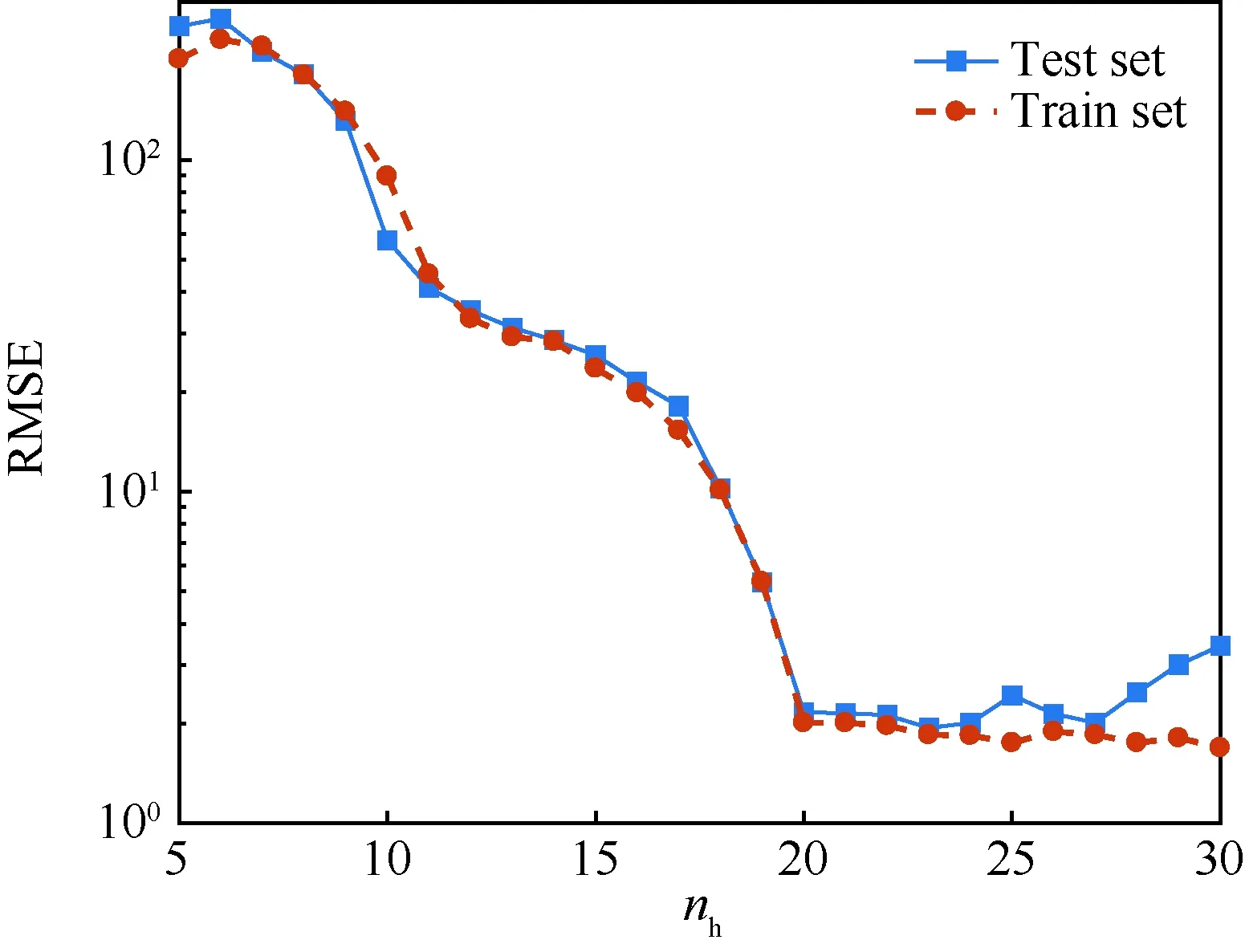
圖13 隱藏層神經元個數-均方根誤差Fig.13 Number of hidden layer neurons vs RMSE

圖14 剩余飛行時間預估效果Fig.14 Test results of estimated time-to-go

2) 再入終段為了到達目標點需要一定的視線角限制，不對最終角度進行調整。

3) 調整區域為中間段寬度x，由式(32)得到時間誤差Δtco,Δtco<0時，說明以當前視線角走廊飛行，最終再入時間將小于期望飛行時間，需要沿①方向擴大走廊以延長再入時間；同理當Δtco>0時，沿②方向縮小視線角走廊以縮短再入飛行時間。

(38)

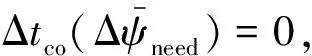
(39)

(40)

(41)

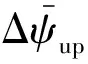
(42)

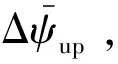
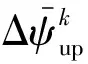
4 仿真驗證

針對設計的時間可控再入制導律和協同結構，首先進行標稱環境下多任務仿真，驗證時間可控再入制導律的自主性與時間可控性；進而進行蒙特卡羅仿真，驗證時間可控再入制導律在參數拉偏情況下的魯棒性；最后進行協同再入仿真，驗證整套協同結構的有效性。

由于飛行器控制能力有限，需要對時間調節范圍進行限制。本文可行時間調節范圍為初始預估飛行時間的0%～4%。不確定性參數采用正態分布，具體如表3所示；再入任務如表4所示。

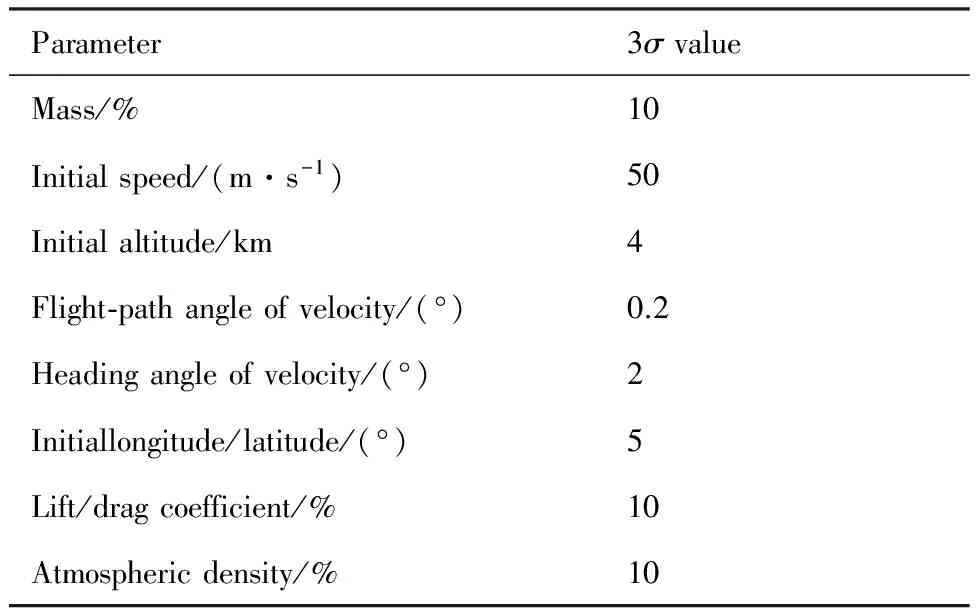
表3 拉偏參數表Table 3 Parameter deviation

表4 再入任務Table 4 Cases of reentry mission

4.1 多任務仿真

在標稱環境下進行多任務指定再入時間仿真，測試時間可控再入制導律的自主性，飛行軌跡如圖15所示。以Case 2為例，再入過程中的具體參數如圖16～圖18。飛行時間誤差、制導精度與制導周期平均耗時的對比如表5所示，其中以文獻[11]為代表的再入制導律記為“制導律1”(Law 1)，本文的再入制導律記為“制導律2”(Law 2)，二者均在相同軟硬件條件下仿真。由圖15(b)的軌跡可知，文獻[20]中的初始投放條件較為保守，對于飛行過程約束留有較大余量，為進一步測試本文制導律的約束管理能力，加入表3的參數拉偏并將Case 2的初始投放條件改為150 km、6 500 m/s，約束校正效果如圖19所示，其中終端約束為16 km、850 m/s。

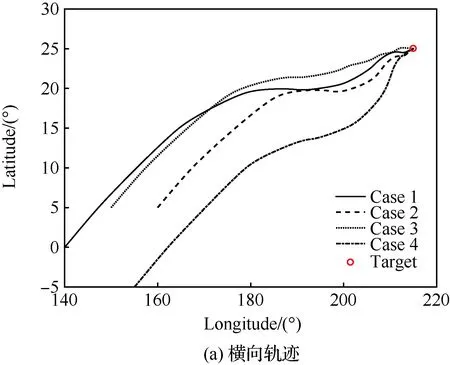
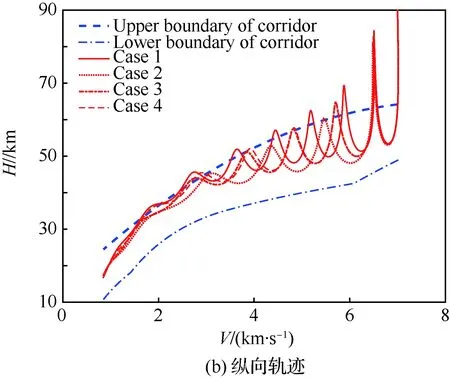
圖15 橫向和縱向軌跡Fig.15 Horizonfal and longitudinal trajectory

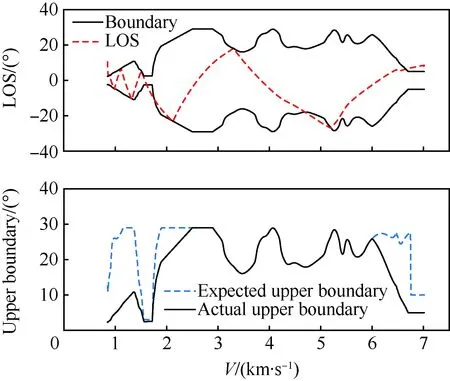
圖16 視線角與走廊變化曲線Fig.16 Changing curves of LOS and corridor

圖17 速度-傾側角剖面Fig.17 Velocity-bank angle profile

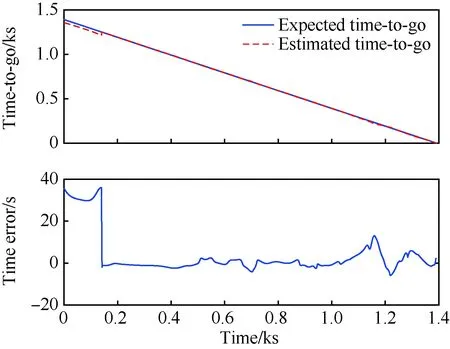
圖18 剩余飛行時間估計效果(Case 2)Fig.18 Test resuts of estimated of time-to-go (Case 2)

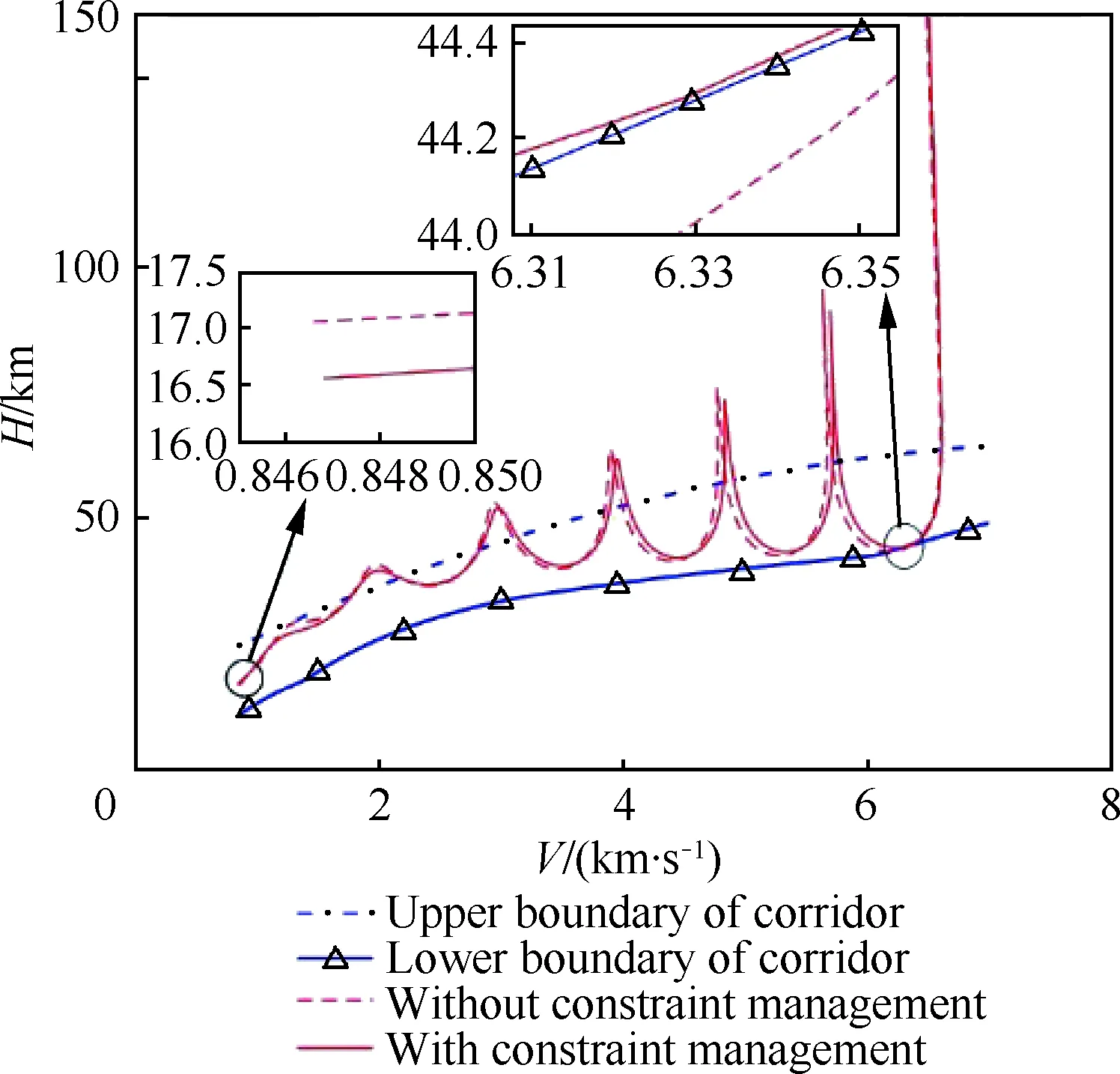
圖19 有無在線約束效果對比Fig.19 Comparison of results with and without online constraint management

表5 多任務仿真結果Table 5 Results of multitasking simulation

在初始下滑段，由于飛行器氣動能力弱，采取大攻角、固定傾側角、固定視線角走廊的方式進行再入飛行，因而產生了圖 18中的預估時間誤差；在進入平衡滑翔段之后，各校正模塊工作，預估時間誤差快速收斂并穩定趨向于零。與此同時，由于真實走廊存在如圖 7所示的線性連接區域，而時間校正模塊直接輸出的是視線角走廊中間段的寬度x，因而會產生如圖 16所示的在初始下滑段和再入終段期望視線角走廊與實際不符的情況。圖 16中的再入橫側向走廊在再入時間預估-校正模塊的作用下呈現不規則的外形，其正是對時間誤差進行主動調節的有效證明。圖 17表明傾側角翻轉次數在可接受的范圍之內。表 5說明時間可控再入制導律在多任務下均有良好的時間控制能力與較高的制導精度，并且本文預測-校正方法的制導周期平均耗時相對于傳統方法縮短了80%以上；圖 18說明在線約束強化管理模塊的加入，有效地改善了飛行過程中約束違反現象的發生，并且對于終端狀態約束的滿足提供了更好保障。

4.2 蒙特卡羅仿真

本節以Case 2為對象，記無時間預估-校正模塊的制導律為“制導律 3”(Law 3)，時間可控再入制導律為“制導律 4”(Law 4)。在可行時間范圍內(1 355～1 408 s)隨機選擇4個期望時間進行蒙特卡羅仿真，以驗證時間可控再入制導律的魯棒性。拉偏參數見表3，兩種制導律在每個期望飛行時間下的仿真次數均為1 000次，最終飛行時間和距離誤差的對比如表6所示。以1 390 s為例，時間可控再入制導律軌跡與時間誤差如圖20～圖22所示。

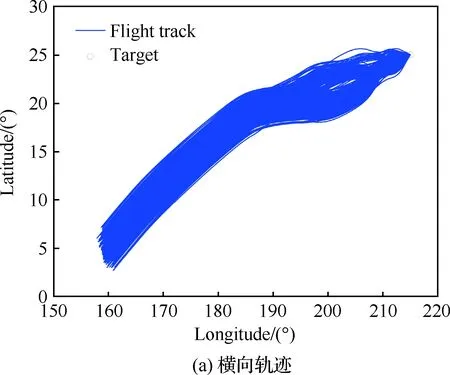
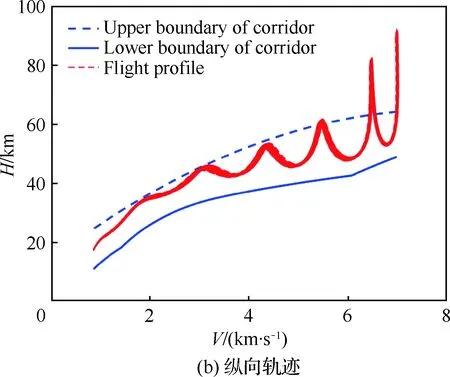
圖20 橫向和縱向軌跡(Case 2)Fig.20 Horizontal and longitudinal trajectory (Case 2)

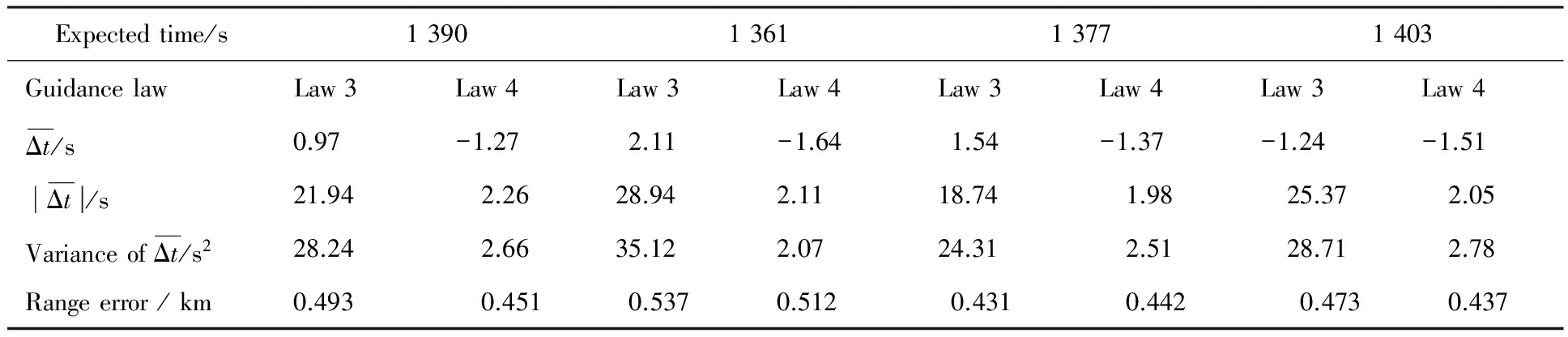
表6 蒙特卡羅仿真結果Table 6 Monte Carlo simulation results

圖22說明再入飛行時間誤差在±10 s以內，滿足協同任務需求[3-4]；通過表6的對比可知，時間可控再入制導律可以有效地降低飛行時間誤差，并且不會影響制導精度。由仿真可知，時間可控再入制導律在參數不確定性下仍有良好的表現，具有一定的魯棒性。其主要原因有：

1) 雖然時間預估網絡來源于離線訓練，但其本身具有一定的泛化能力[22]和較高的精度。

2) 時間預估網絡的輸入來源于實際飛行狀態，而參數不確定性所帶來的干擾直接影響當前飛行狀態，使其偏離期望值，進而間接地影響預估時間結果，從而產生時間誤差。

3) 長距離的飛行過程、軌跡預測校正和時間校正模塊的在線迭代使得誤差能及時得到修正。

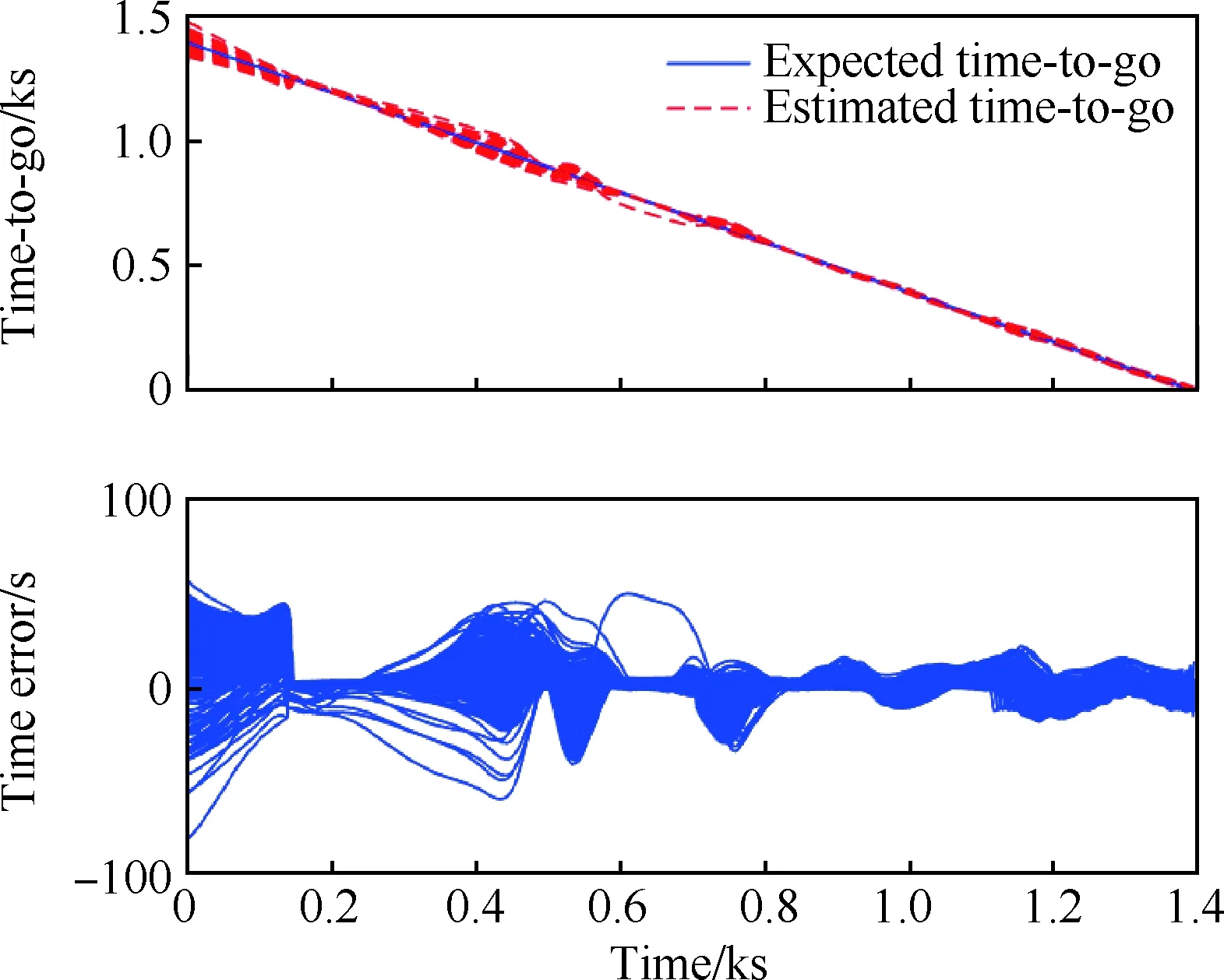
圖21 剩余飛行時間估計效果(Case 2)Fig.21 Estimated time-to-go (Case 2)

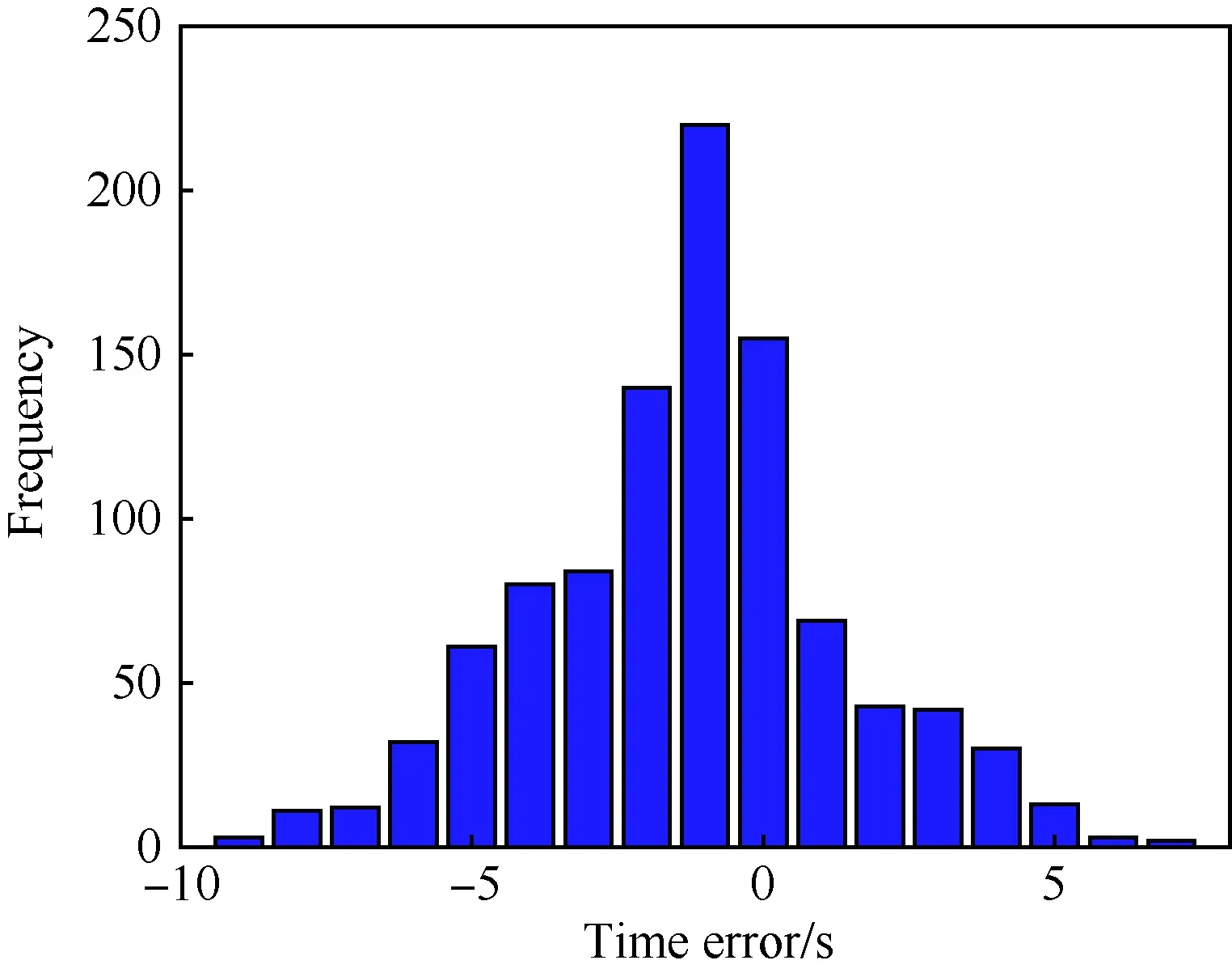
圖22 最終飛行時間誤差直方圖Fig.22 Histogram of final flight time error

4.3 協同再入仿真

針對多高超聲速飛行器協同再入任務需求，在協調時間存在的前提下，隨機選擇5個初始投放點，進行協同再入仿真以驗證協同結構的有效性。參數拉偏如表3所示，各飛行器之間相互獨立。最終期望協同再入時間為1 702.8 s。最終再入軌跡與協調時間變化曲線如圖23和圖24所示，協同再入結果如表7所示。

仿真結果表明在整個飛行過程中，期望協同飛行時間信息相對平滑，各飛行器的實際飛行時間均能趨向于期望值。其中在平衡滑翔段，由于參數不確定性等原因的干擾，使得部分飛行器預估時間出現較大誤差，但通過時間校正模塊和協同結構的共同作用可以有效地將其進行消除。整個飛行過程表明協同結構可以有效的對可協同的多個飛行器進行協調時間計算，而時間可控再入制導律可以有效地將時間協調信息作為約束之一進行實時的在線軌跡預測與校正，實現多飛行器協同再入任務需求。

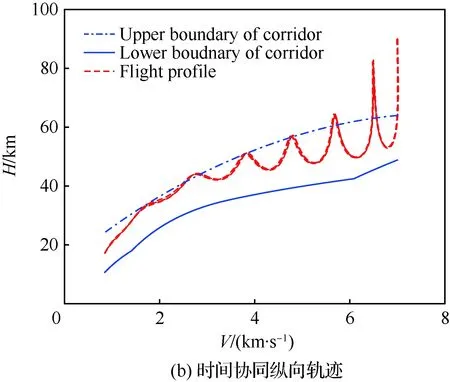
圖23 時間協同橫向和縱向軌跡Fig.23 Time-coordinated horizontal and longitudinal trajectory

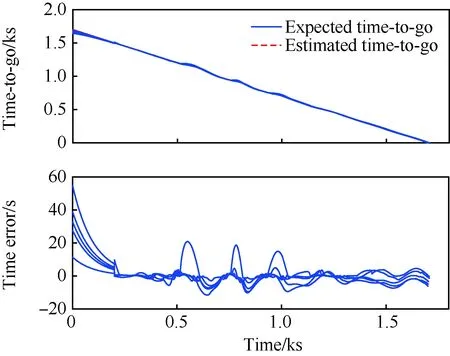
圖24 剩余飛行時間估計效果(時間協同)Fig.24 Estimation of time-to-go (time-coordinated)

表7 協同再入結果Table 7 Results of collaborative reentry flight

5 結 論

1) 本文針對多高超聲速飛行器時間協同再入制導問題，提出協同再入制導架構和時間可控再入制導律。

2) 時間可控再入制導律在跨周期軌跡預測-校正制導律的基礎上，通過對時間影響因素的仿真與分析，將橫向制導模塊中的視線角走廊寬度作為控制量，利用神經網絡和Gauss-Newton迭代法實現再入飛行時間的預估與校正。

3) 時間可控再入制導律根據當前實時的飛行狀態進行時間預估，得到時間誤差并由此對視線角走廊進行動態調整，仿真驗證了其具有良好的自主性、魯棒性、實時性和時間可控性。

4) 協同再入制導架構分為兩層，適用于集中式或分布式的通訊結構。上層協調層的協同函數可以根據飛行任務需求進行有針對性設計；下層執行層由時間可控再入制導律進行在線軌跡規劃。仿真驗證了該結構的有效性，能夠實現多高超聲速飛行器的協同再入飛行任務需求。

參 考 文 獻

[1] 胡冬冬, 劉曉明, 張紹芳, 等. 2016年國外高超聲速飛行器技術發展綜述[J]. 戰術導彈技術, 2017(1): 28-33.

HU D D, LIU X M, ZHANG S F, et al. Review of hypersonic technologies progress abroad in 2016[J]. Tactical Missile Technology, 2017(1): 28-33 (in Chinese).

[2] 高雁翎, 張夢湉, 賈晨陽. 2016年國外防空反導發展綜述[J]. 戰術導彈技術, 2017(2): 16-20.

GAO Y L, ZHANG M T, JIA C Y. Development review of world air and missile defense system in 2016[J]. Tactical Missile Technology, 2017(2): 16-20 (in Chinese).

[3] 李聰穎, 韓蕾, 高曉冬, 等. 再入反艦導彈多彈協同飽和攻擊突防最優彈道研究[J]. 指揮與控制學報, 2015, 1(1): 72-80.

LI C Y, HAN L, GAO X D, et al. Study on optimalpe-netration trajectories of multi reentry anti-ship missiles for cooperative saturation attack[J]. Journal of comma-nd and control, 2015, 1(1): 72-80 (in Chinese).

[4] 王少平, 董受全, 李曉陽, 等. 助推滑翔高超聲速反艦導彈多方向協同突防可行性研究[J]. 指揮控制與仿真, 2017, 39(2): 55-60.

WANG S P, DONG S Q, LI X Y, et al. Feasibility study of multi-direction coordinated penetration of the boost-glide hypersonic anti-ship missile[J]. Command Control and Simulation, 2017, 39(2): 55-60 (in Chinese).

[5] JEON I S, LEE J I, TAHK M J. Impact-time-control guidance law for anti-ship missiles[J]. IEEE Transactions on Control Systems Technology, 2006, 14(2): 260-266.

[6] 趙世鈺, 周銳. 基于協調變量的多導彈協同制導[J]. 航空學報, 2008, 29(6):1605-1611.

ZHAO S Y, ZHOU R. Multi-missile cooperativeguid-ance using coordination variables[J]. Acta Aeronautica et Astronautica Sinica, 2008, 29(6): 1605-1611 (in Chinese).

[7] ZHAO S Y, ZHOU R. Cooperativeguidance for multi-missile salvo attack[J]. Chinese Journal of Aeronautics, 2008, 21(6): 533-539.

[8] MCLAIN T W, BEARD R W. Coordinationvariables, coordination functions, and cooperative timing mission[J]. Journal of Guidance Control & Dynamics, 2005, 28(1): 150-161.

[9] 張友安, 馬國欣, 王興平. 多導彈時間協同制導: 一種領彈-被領彈策略[J]. 航空學報, 2009, 30(6): 1109-1118.

ZHANG Y A, MA G X, WANG X P. Time-cooperative guidance for multi-missiles: A Leader-Follower strategy[J]. Acta Aeronautica et Astronautica Sinica, 2009, 30(6): 1109-1118 (in Chinese).

[10] 趙啟倫, 陳建, 李清東, 等. 高超武器與常規導彈協同攻擊策略可行域研究[J]. 航空學報, 2015, 36(7): 2291-2300.

ZHAO Q L, CHEN J, LI Q D, et al. Feasible region of hypersonic and ballistic missiles’ cooperative attack strategy[J]. Acta Aeronautica et Astronautica Sinica, 2015, 36(7): 2291-2300 (in Chinese).

[11] LU P. Entry guidance: A unifiedmethod[J]. Journal of Guidance Control & Dynamics, 2014, 37(3): 713-728.

[12] 劉思源, 梁子璇, 任章, 等. 高超聲速滑翔飛行器再入段制導方法綜述[J]. 中國空間科學技術, 2016, 36(6): 1-13.

LIU S Y, LIANG Z X, REN Z, et al. Review of reentry guidance methods for hypersonic gliding vehicles[J]. Chinese Space Science and Technology, 2016, 36(6): 1-13 (in Chinese).

[13] WANG Z, GRANT M J. Constrained trajectory optimiza-tion for planetary entry via Sequential convex program-ming[C]∥AIAA Atmospheric Flight Mechanics Conference. Reston, VA: AIAA, 2017: 1-13.

[14] CHENG L, WANG Z, CHENG Y, et al.Multiconstrain-ed predictor-corrector reentry guidance for hypersonic vehicles[J]. Proceedings of the Institution of Mechanical Engineers Part G Journal of Aerospace Engineering, 2017: 095441001772418.

[15] KURIKI Y, NAMERIKAWA T. Consensus-based coop-erative formation control with collision avoidance for a multi-UAV system[C]∥American Control Conference. Piscataway, NJ: IEEE Press, 2014: 2077-2082.

[16] BRARD R W, MCLAIN T W, GOODRICH M A, et al. Coordinated target assignment and intercept for unmanned air vehicles[J]. IEEE Transactions on Robotics & Automation, 2002, 18(6): 911-922.

[17] TOMIC S, BEKO M, RUI D. RSS-Based localization in wireless sensor networks using convex relaxation: noncooperative and cooperative schemes[J]. IEEE Transactions on Vehicular Technology, 2015, 64(5): 2037-2050.

[18] SHI P, SHEN Q. Cooperative control of multi-agent systems with unknown state-dependent controlling effects[J]. IEEE Transactions on Automation Science & Engineering, 2015, 12(3): 827-834.

[19] 林濤, 劉永才, 關成啟, 等. 飛航導彈協同作戰使用方法探討[J]. 戰術導彈技術, 2005(2): 8-12.

LIN T, LIU Y C, GUAN C Q, et al. An investigation into the methods of cooperative engagenment for aerodynamic missile[J]. Tactical Missile Technology, 2005(2): 8-12 (in Chinese).

[20] 王光倫. 高超聲速飛行器再入段預測校正制導研究[D]. 哈爾濱: 哈爾濱工業大學, 2010: 18-19.

WANG G L. Predictor-corrector reentry guidance for hypersonic vehicles[D].Harbin: Harbin Institute of Technology, 2010: 18-19 (in Chinese).

[21] PHILLIPS T H. A common aero vehicle (CAV) model, description, and employment guide[R]. Albuqerque, New Mexico: Schafer Corp-oration for AFRL and AFSPC, 2003.

[22] SUTTON R, BARTO A. Reinforcement Learning: An Introduction[M]. Massachusetts: MIT Press, 2005: 235-304.

[23] DU X, GAO M F.The application of identifying numbers on artificial neural network[J]. Computer Systems Applications, 2007(2): 21-22.