一種改進(jìn)的蟻群路徑規(guī)劃算法

王天生，張 峰

（1.上汽通用五菱汽車股份有限公司，廣西 柳州 545000；2.武漢理工大學(xué)機(jī)電工程學(xué)院，湖北 武漢 430070）

0 引言

近年來隨著移動機(jī)器人技術(shù)的大量應(yīng)用，作為其重要分支的路徑規(guī)劃技術(shù)也受到了學(xué)者的廣泛關(guān)注。所謂路徑規(guī)劃即是在充滿障礙物的規(guī)劃空間中找到一條從起點(diǎn)到終點(diǎn)的最優(yōu)、最短路徑，并且能夠無碰撞地成功地繞開環(huán)境中所有的障礙物。目前，在路徑規(guī)劃領(lǐng)域中應(yīng)用的比較多的算法主要分為兩類，一類是可視圖法[1]、自由空間法[2]、拓?fù)鋱D法等傳統(tǒng)的求解方法；另一類則是采用遺傳算法、蟻群算法、神經(jīng)網(wǎng)絡(luò)法等智能算法。雖然上述的各種方法為路徑規(guī)劃問題提供了不同的解決方案，但是各種方法在執(zhí)行上總是存在著不同的缺點(diǎn)與優(yōu)點(diǎn)，并沒有一種方法能夠完全適應(yīng)各種環(huán)境條件下的任何系統(tǒng)。

蟻群算法是一種模擬螞蟻群體覓食行為的仿生優(yōu)化算法，該算法具有較強(qiáng)的魯棒性、優(yōu)良的分布式計(jì)算機(jī)制、易于與其他算法相結(jié)合等優(yōu)點(diǎn)[3]。因此，自意大利的Dorigo[4]學(xué)者提出蟻群算法以來，如今已經(jīng)在各行各業(yè)得到了廣泛的應(yīng)用。但傳統(tǒng)的蟻群算法由于其復(fù)雜性往往需要很長的搜索時(shí)間，而算法搜索初期的盲目性也容易造成算法收斂速度慢等缺點(diǎn)[5]。針對上述缺點(diǎn)，許多學(xué)者也提出了相應(yīng)的改進(jìn)方法，如Stutzle[6]為了避免蟻群算法趨于停滯、陷于局部最優(yōu)，對信息素的更新范圍進(jìn)行了限定，從而提出了搜索效果更好的最大最小螞蟻系統(tǒng)（MMAS）。黃震等[7-9]學(xué)者則是將蟻群算法與其他表現(xiàn)較好優(yōu)化算法如遺傳算法、A*算法等相結(jié)合，從而提出了收斂性較好的混合蟻群算法。大量的文獻(xiàn)[10]也表明，多數(shù)學(xué)者對蟻群算法的改進(jìn)主要聚焦于信息素的更新方式以及怎樣提高種群的多樣性，很少有學(xué)者關(guān)注螞蟻的搜索方向以及啟發(fā)函數(shù)信息的更新。因此，本文基于傳統(tǒng)的蟻群算法加入了自適應(yīng)調(diào)整啟發(fā)函數(shù)，局部最優(yōu)方向引導(dǎo)機(jī)制，并在此基礎(chǔ)上提出了一種改進(jìn)的蟻群路徑規(guī)劃算法，該算法具有較高的收斂速度。

1 傳統(tǒng)的蟻群路徑規(guī)劃算法

雖然蟻群算法的提出是著眼于解決旅行商問題（TSP），但其基本思想?yún)s可以應(yīng)用于許多其他問題的求解，路徑規(guī)劃問題便是其中之一。因此，基于蟻群算法的路徑規(guī)劃也得到了大量的發(fā)展，蟻群算法中最重要的是螞蟻對下一步節(jié)點(diǎn)的概率的選擇以及各節(jié)點(diǎn)之間的信息素的更新。

1.1路徑選擇概率

螞蟻 k（k=1，2，…，m）在運(yùn)動過程中，根據(jù)各路徑上的信息素量來決定下一步的轉(zhuǎn)移節(jié)點(diǎn)，其中用禁忌表tabuk表示螞蟻k所走過的節(jié)點(diǎn)集合，禁忌表會在螞蟻移動過程中做動態(tài)調(diào)整，在路徑搜索過程中，螞蟻根據(jù)各路徑上的信息量以及路徑的啟發(fā)信息來計(jì)算狀態(tài)轉(zhuǎn)移概率。表示t時(shí)刻螞蟻k由節(jié)點(diǎn)i轉(zhuǎn)移到節(jié)點(diǎn)j的狀態(tài)轉(zhuǎn)移概率，其公式如式（1）所示。

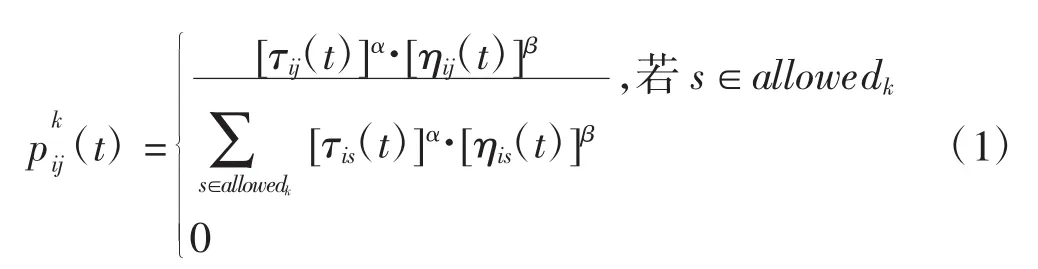
否則式中，allowedk＝{C-tabuk}表示螞蟻k下一步允許選擇的節(jié)點(diǎn)，α為信息啟發(fā)式因子，表示各節(jié)點(diǎn)間信息的相對重要性，反映了螞蟻在運(yùn)動過程中所累積的信息在螞蟻運(yùn)動時(shí)所起到的作用，其值越大，則螞蟻越傾向于其他螞蟻所走過的路徑，螞蟻之間的協(xié)作性也就越強(qiáng)，但過大的信息啟發(fā)因子也會限制蟻群算法的全局搜索能力。β為期望式啟發(fā)因子，反映了啟發(fā)信息在螞蟻選擇路徑中受重視的程度，其值越大，則蟻群算法越接近于貪心算法。ηij（t）為啟發(fā)函數(shù)，在路徑規(guī)劃中，一般其表達(dá)式如式（2）：

式中，dij表示兩節(jié)點(diǎn)之間的歐式距離。

1.2信息素的更新

蟻群算法中螞蟻群體的協(xié)作離不開信息素，但無限量的累加各節(jié)點(diǎn)上的信息素量不僅不符合螞蟻群體的自然規(guī)律，也會造成信息素過多而淹沒啟發(fā)信息，因此，當(dāng)所有螞蟻到達(dá)終點(diǎn)后就要對全局信息素進(jìn)行更新。其更新不僅包含信息素的累加，也包含信息素的揮發(fā)。各節(jié)點(diǎn)之間的信息素可按如公式（4）（5）執(zhí)行：

式中，ρ表示信息素?fù)]發(fā)系數(shù)，用于衡量信息素的衰減程度，其取值范圍一般為ρ∩（0，1）表示本次循環(huán)中路徑（i，j）上的信息素增量表示螞蟻群體中第k只螞蟻在本次循環(huán)中留在路徑（i，j）上的信息量，如式（6）所示：

否則式中，Q表示信息素強(qiáng)度，其值大于0，Lk表示第k只螞蟻在本次循環(huán)中所走路徑的總長度。

2 改進(jìn)的蟻群路徑規(guī)劃算法

2.1自適應(yīng)調(diào)整啟發(fā)函數(shù)

在傳統(tǒng)的蟻群算法中，由于啟發(fā)函數(shù)ηis（t）對終點(diǎn)的指向性較差，從而導(dǎo)致算法搜索時(shí)間長，收斂速度慢，因此，考慮在算法搜索初期以待選節(jié)點(diǎn)與終點(diǎn)之間歐式距離的倒數(shù)作為新的啟發(fā)函數(shù)，如式（7）所示。

式中，djd表示節(jié)點(diǎn)j與終點(diǎn)d的歐式距離。

在實(shí)際的路徑規(guī)劃中，由于搜索空間中各種障礙物的影響，以歐式距離作為待選節(jié)點(diǎn)與終點(diǎn)之間的最短可行路徑并不利于散發(fā)后期的快速收斂，故將式（7）中的啟發(fā)函數(shù)應(yīng)用于算法搜索于初期階段，隨著算法迭代次數(shù)的增加，各代中的最優(yōu)路徑也就更加接近實(shí)際的最短路徑，此時(shí)，啟動啟發(fā)函數(shù)更新機(jī)制，以算法每代的最優(yōu)線路為基礎(chǔ)對啟發(fā)函數(shù)進(jìn)行更新。啟發(fā)函數(shù)的更新公式如（8）（9）（10）所示。

當(dāng) i=start時(shí)，則公式（9）變?yōu)槿缦鹿剑?0）所示。

式中，NC表示算法迭代次數(shù)；djd（t，NC）表示在算法迭代NC次時(shí)，節(jié)點(diǎn)j與終點(diǎn)d之間的最短可行路徑；η″ij（t，NC）表示更新后的啟發(fā)函數(shù)，R_best（NC）表示在NC中的最優(yōu)線路；i，j分別表示R_best（NC）中相鄰的兩節(jié)點(diǎn)，其中i節(jié)點(diǎn)在前，j節(jié)點(diǎn)在后；start表示起始點(diǎn)；dsj表示起始點(diǎn)與節(jié)點(diǎn)j之間的歐式距離；dij表示相鄰節(jié)點(diǎn)i，j之間的歐式距離。在動態(tài)調(diào)整啟發(fā)函數(shù)后，螞蟻搜索過程中的狀態(tài)轉(zhuǎn)移概率如公式（11）所示。

否則式中，const為一常數(shù)，其值大于0；NC為算法迭代次數(shù)。

2.2局部方向引導(dǎo)機(jī)制

在傳統(tǒng)的蟻群算法中，螞蟻的狀態(tài)轉(zhuǎn)移概率的主要影響因素是信息素與啟發(fā)函數(shù)，但路徑規(guī)劃問題最大的不同是在路徑規(guī)劃前有事先可知的起始點(diǎn)與終點(diǎn)。因此，處在當(dāng)前節(jié)點(diǎn)i的螞蟻在搜索轉(zhuǎn)移節(jié)點(diǎn)時(shí)，則可認(rèn)為當(dāng)前節(jié)點(diǎn)i與目標(biāo)點(diǎn)d的連線方向?yàn)樽顑?yōu)的搜索方向。轉(zhuǎn)移節(jié)點(diǎn)j的優(yōu)劣以當(dāng)前節(jié)點(diǎn)i分別與轉(zhuǎn)移節(jié)點(diǎn)j和目標(biāo)點(diǎn)d連線向量的夾角θijd來衡量。θijd越小，則轉(zhuǎn)移節(jié)點(diǎn)越靠近最優(yōu)的搜索方向。在綜合考慮信息素，自適應(yīng)的啟發(fā)函數(shù)以及局部最優(yōu)的搜索方向后，改進(jìn)的路徑選擇概率如公式（12）所示。

否則式中，λ表示局部方向因素強(qiáng)度系數(shù)，其值大于0.γ表示局部方向因素衰減系數(shù)，其值大于1.θijd表示i與終點(diǎn)d的連線向量與i到j(luò)連線向量的夾角。從公式（12）可知，γ值的大小影響著局部方向因素的衰減程度。由于在蟻群算法的初級階段，各節(jié)點(diǎn)之間信息素差異較小，轉(zhuǎn)移概率隨機(jī)性較大，算法收斂速度較低，這時(shí)可通過加大局部方向因素的影響，使螞蟻更多的向最優(yōu)路線聚集，算法的后期，則應(yīng)逐漸降低局部方向因素的影響，從而讓信息素和啟發(fā)函數(shù)成為轉(zhuǎn)移概率選擇的主導(dǎo)因素，因此，合理的選擇參數(shù)λ，γ的值非常的重要。

3 仿真測試

為了驗(yàn)證改進(jìn)的蟻群算法在機(jī)器人路徑規(guī)劃中的有效性，本文利用Matlab2010仿真軟件在如圖1所示的兩種復(fù)雜度不同的柵格環(huán)境下進(jìn)行了路徑規(guī)劃的仿真（柵格中黑色代表障礙物），并記錄了對應(yīng)的最優(yōu)路徑迭代收斂曲線。從圖中可以看出，環(huán)境1為的柵格環(huán)境，環(huán)境中的障礙物也較少，環(huán)境2則為的柵格環(huán)境，規(guī)劃空間也更為復(fù)雜。在記錄各算法在各環(huán)境下的最優(yōu)路徑迭代曲線時(shí)，考慮到蟻群算法的隨機(jī)性，選取了各算法的20次試驗(yàn)的平均值作為參考數(shù)據(jù)。算法中各參數(shù)的取值分別為螞蟻數(shù)m=30，α ＝ 1，β ＝ 6，ρ＝ 0.1，Q ＝ 14，λ ＝ 3，γ ＝ 4，const=10，柵格環(huán)境1中算法的最大循環(huán)次數(shù)NCmax1=50，柵格環(huán)境2中算法的最大循環(huán)次數(shù)NCmax1=100.

圖1 不同的仿真測試柵格環(huán)境

圖2為兩種算法在環(huán)境1下的最優(yōu)規(guī)劃路徑，圖3分別為傳統(tǒng)算法與改進(jìn)算法在環(huán)境1下的最優(yōu)路徑迭代收斂曲線。從圖中可以看出，兩種算法雖然都環(huán)境1下找到了最優(yōu)的規(guī)劃路徑，但改進(jìn)算法在迭代9次時(shí)收斂，而傳統(tǒng)算法則是23次。因此改進(jìn)的蟻群算法較傳統(tǒng)的算法在收斂速度上具有不小的優(yōu)勢，收斂速度更快。

圖2 環(huán)境1下的最優(yōu)規(guī)劃路徑

圖3 環(huán)境1下兩算法的最優(yōu)路徑迭代收斂曲線

圖4為兩種算法在環(huán)境2下的最優(yōu)規(guī)劃路徑，圖5則分別為傳統(tǒng)算法與改進(jìn)算法在環(huán)境2下的最優(yōu)路徑迭代收斂曲線。從圖中可以看出改進(jìn)的算法在迭代38次時(shí)收斂，傳統(tǒng)算法則要迭代75次才收斂。因此，改進(jìn)算法較傳統(tǒng)算法收斂更快。從上述的仿真測試可以看出，改進(jìn)的蟻群路徑規(guī)劃算法不僅適應(yīng)簡單的規(guī)劃環(huán)境，在復(fù)雜的環(huán)境中較傳統(tǒng)算法也有較快的收斂速度。

圖4 環(huán)境2下的最優(yōu)規(guī)劃路徑

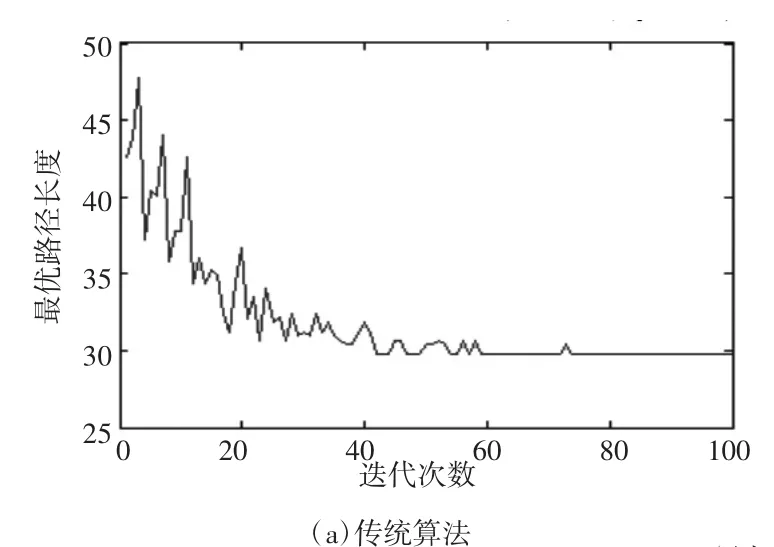
（續(xù)下圖）

（接上圖）

圖5 環(huán)境2下兩算法的最優(yōu)路徑迭代收斂曲線

4 結(jié)束語

針對將傳統(tǒng)的蟻群算法應(yīng)用到機(jī)器人路徑規(guī)劃中易出現(xiàn)搜索時(shí)間長，收斂速度慢等問題，本文提出了一種改進(jìn)的蟻群路徑規(guī)劃算法。改進(jìn)的蟻群算法能自適應(yīng)的調(diào)整啟發(fā)函數(shù)，并加入了動態(tài)衰減的局部方向引導(dǎo)機(jī)制。在算法搜索初期，以搜索節(jié)點(diǎn)與終點(diǎn)的歐式距離的倒數(shù)表示取法函數(shù)，在算法迭代到一定階段后，以各代的最優(yōu)路徑信息動態(tài)地更新啟發(fā)函數(shù)信息。以搜索節(jié)點(diǎn)與終點(diǎn)連線的方向?yàn)樽顑?yōu)的搜索方向，并引入了局部方向因素強(qiáng)度系數(shù)、局部方向因素衰減系數(shù)，并借此構(gòu)建了新的路徑選擇概率表達(dá)式。仿真測試表明，改進(jìn)的蟻群路徑規(guī)劃算法在各種不同的規(guī)劃環(huán)境中都有較快的收斂速度。

參考文獻(xiàn)：

[1]李善壽，方潛生，肖本賢，等.全局路徑規(guī)劃中基于改進(jìn)可視圖法的環(huán)境建模[J].華東交通大學(xué)學(xué)報(bào)，2008，25（06）：73-77.

[2]熊 菡.移動機(jī)器人全局路徑規(guī)劃及軌跡跟蹤研究[D].武漢：武漢科技大學(xué)，2014.

[3]金 弟，楊 博，劉 杰，等.復(fù)雜網(wǎng)絡(luò)簇結(jié)構(gòu)探測——基于隨機(jī)游走的蟻群算法[J].軟件學(xué)報(bào)，2012（03）：451-464.

[4]Dorigo M，Gambardella L M.Ant colony system：A coopera tive learning approach to the traveling salesman problem[J].IEEE Trans on Evolutionary Computation，1997，1（1）：53-66.

[5]馬金財(cái).基于蟻群算法的機(jī)器人路徑規(guī)劃問題研究[D].昆明：昆明理工大學(xué)，2014.

[6]Thomas Stutzle T，Holger H Hoos.Max-min ant system[J].Future Generation Computer Systems， 2000，16（8）：889-914.

[7]蘇海鋒，許道林，李汶江，等.基于改進(jìn)蟻群A～*算法的輸電線路路徑搜索[J].河北大學(xué)學(xué)報(bào)（自然科學(xué)版），2017，37（01）：92-100.

[8]黃 震，羅中良，黃時(shí)慰.一種帶時(shí)間窗車輛路徑問題的混合蟻群算法[J].中山大學(xué)學(xué)報(bào)（自然科學(xué)版），2015，54（01）：41-46.

[9]薛冰冰.基于改進(jìn)型遺傳算法的足球機(jī)器人路徑規(guī)劃研究[D].長春：長春工業(yè)大學(xué)，2012.

[10]朱顥東，孫 振，吳 迪.基于改進(jìn)蟻群算法的移動機(jī)器人三維路徑規(guī)劃[J].華中師范大學(xué)學(xué)報(bào)（自然科學(xué)版），2016，50（06）：812-817.