基于函數值的有理插值曲面及其約束控制

劉 植,肖 凱,江 平,謝 進

(1.合肥工業大學數學學院,安徽合肥 200009)

(2.合肥學院科學計算研究所,安徽合肥 230601)

1 引言

曲面的數學描述是計算機輔助幾何設計和計算機圖形學的重要研究方向.傳統的曲面設計工具多采用多項式插值樣條方法,但對于給定的插值條件,生成的插值函數是唯一確定的,形狀修改與控制不夠靈活.隨著CAD/CAM技術的發展,包含B′ezier、B樣條方法的非均勻有理B樣條(NURBS)方法已被廣泛的應用到工業產品如輪船、汽車、飛機等形狀造型的設計.然而,這些方法得到曲面的局部修改與約束控制同樣面臨挑戰.近年來,有關單變量有理插值方法的研究在一定程度上解決了局部修改與控制的問題,取得了重要進展[1].如劉愛奎在文[2]中提出帶有形狀參數的加權有理插值曲線不僅具有簡潔的表達式,同時可以讓曲線整體約束于折線之間,并具有局部點控制能力.Erge[3]分析了C1條件下線性有理樣條的兩點邊值問題.Han[4]研究了一類C2連續有理三次保凸逼近方法及性質.

關于雙變量樣條函數的研究也取得了很多成果:Sun[5]提出一種分母(1,0)次分子(3,1)次的三角域有理插值樣條,該方法主要應用于地質勘探、鍛造科技和醫學影像中基于平行線上的散亂數據的插值曲面重構;Duan和他的團隊在二元有理插值樣條研究領域做了大量工作:如在文獻[6]中構造了一類基于函數值和偏導數值分母為雙一次、分子雙三次的二元有理插值樣條,該樣條函數具有簡單對稱的基函數,便于理論研究與曲面局部約束控制;在文獻[7]中給出了僅基于函數值分母為雙一次、分子雙三次的二元有理插值樣條,在文獻[8]中給出了僅基于函數值分母為雙二次、分子雙三次的二元有理插值樣條,并研究了樣條函數的矩陣表示、邊界性質等.鄧四清等構造了僅基于函數值分子分母均為雙三次的二元有理插值曲面樣條[9],以及分母為雙二次分子雙三次的二元有理插值曲面樣條[10,11],并研究了這些曲面的邊界、逼近及中央點約束控制問題.2012年,項梅靈[12]構造了僅基于函數值分母為雙二次、分子雙三次的二元有理插值曲面樣條,并研究了其凸性、邊界插值、極限、解析和正則等性質,同時分析了參數對曲面形狀的控制作用.

加權組合是CAGD中的一種常用造型方法.Huang[13]和Zhang[14]僅基于函數值,先構造了一種分母為(1,0)次、分子雙三次的二元有理插值樣條曲面,另一種分母為(0,1)次、分子雙三次的二元有理插值樣條曲面,然后將兩種樣條曲面加權組合得到一種新的二元有理插值樣條曲面,并討論了曲面的矩陣形式,誤差分析以及局部約束問題.上述二元有理插值構造方法在形式上的共同點是分母為一次、二次或三次,而分子一般是三次或四次.對于給定的插值數據,通過改變參數值可以控制有理插值曲面的形狀.這些有理函數較高的次數帶來了形式以及計算的復雜性.本文僅基于給定函數值,通過對兩種線性有理插值函數的加權組合構造一類新的二元有理插值方法.該有理插值函數具有形式對稱的基函數.對于給定的插值數據,插值曲面形狀的整體與局部控制靈活方便.

2 插值函數

2.1 插值函數的構造

插值函數的構造思路及步驟如下:

(1)在x方向構造分子分母均為一次的有理插值曲線,然后在y方向用線性插值方法構造二元有理插值曲面;

(2)按相反順序構造先y后x方向的二元有理插值曲面;

(3)對上述兩類有理插值函數加權組合構造新的二元有理插值曲面.

設{(xi,yi,fi,j)},i=1,2;j=1,2為給定平面區域D=[x1,x2;y1,y2]上的插值數據點集,x1,x2和y1,y2為插值節點.令h=x2?x1,l=y2?y1,對xy平面上任意點(x,y)∈D,令u=(x?x1)/h,先沿x方向構造線性有理插值曲線

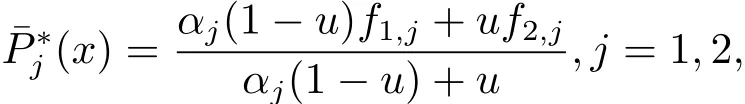
其中αj＞0.顯然,插值函數滿足

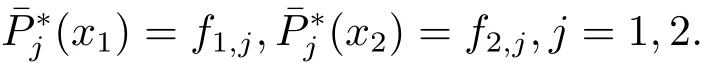
對任意x,可在D上構造二元有理插值函數

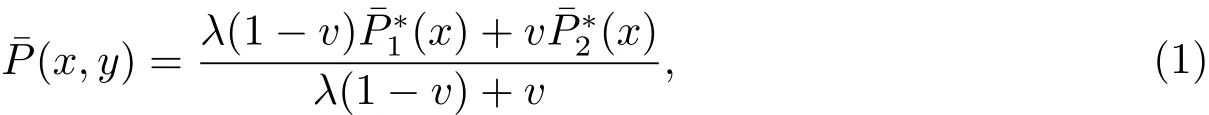
這里v=(y?y1)/l,λ＞0.可以驗證滿足

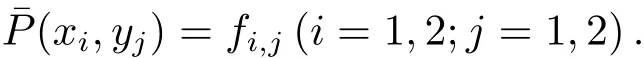
同理,先從y方向構造插值曲線,再從x方向構造插值曲面可以得到另一種二元線性有理插值函數

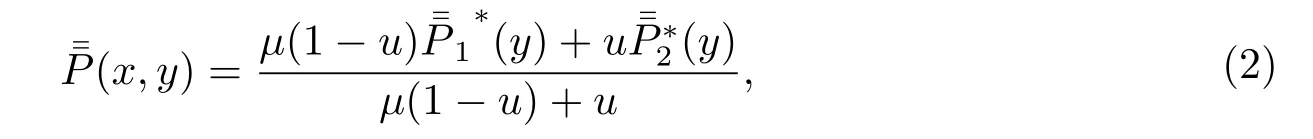
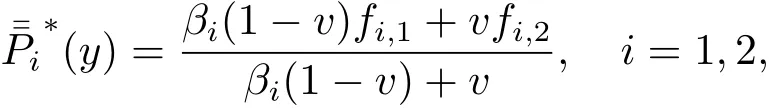
其中βi＞0,μ＞0.可以驗證也滿足

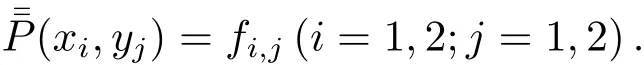
對于任意給定的插值數據點集 {(xi,yj,fi,j)},i=1,2;j=1,2 和正參數 α1,α2,β1,β2,λ,μ,在區域D上的插值函數(x,y)和(x,y)都是唯一的,且無論參數取何正值均滿足插值條件.

基于插值曲面(1)式和(2)式,可以構造新的二元加權有理插值函數

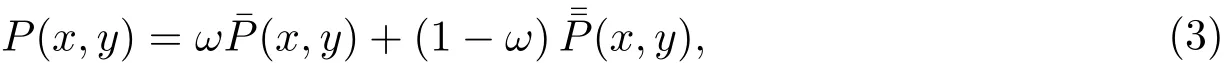
其中ω∈[0,1].該函數滿足插值條件

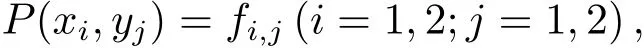
稱α1,α2,β1,β2,λ,μ為形狀參數,ω為權系數,也稱(x,y)和(x,y)為基本曲面(或極限曲面).

2.2 插值基函數

為了便于分析該有理插值函數的性質,將(1)式和(2)式代入到(3)式并化簡,插值函數P(x,y)也可改寫為如下基表示形式

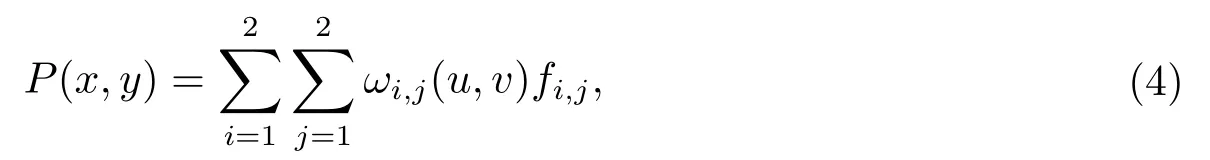
其中

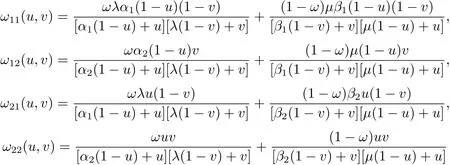
稱為二元加權有理插值函數的基函數,它們滿足

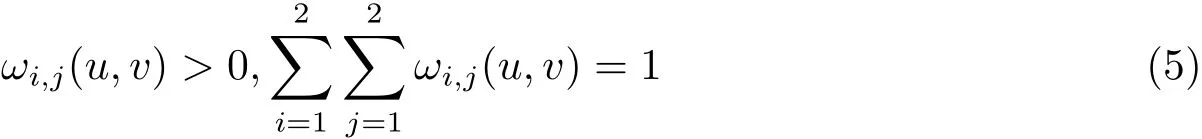
以及對稱性質.圖1所示即為ω=0.5,其余形狀參數均取2時的四個基函數,從左往右,上往下依次是 ω11(u,v),ω12(u,v),ω21(u,v),ω22(u,v).

由(4)式和(5)式可以看出,加權線性有理插值本質上即是對四個插值數據點的一種加權組合.

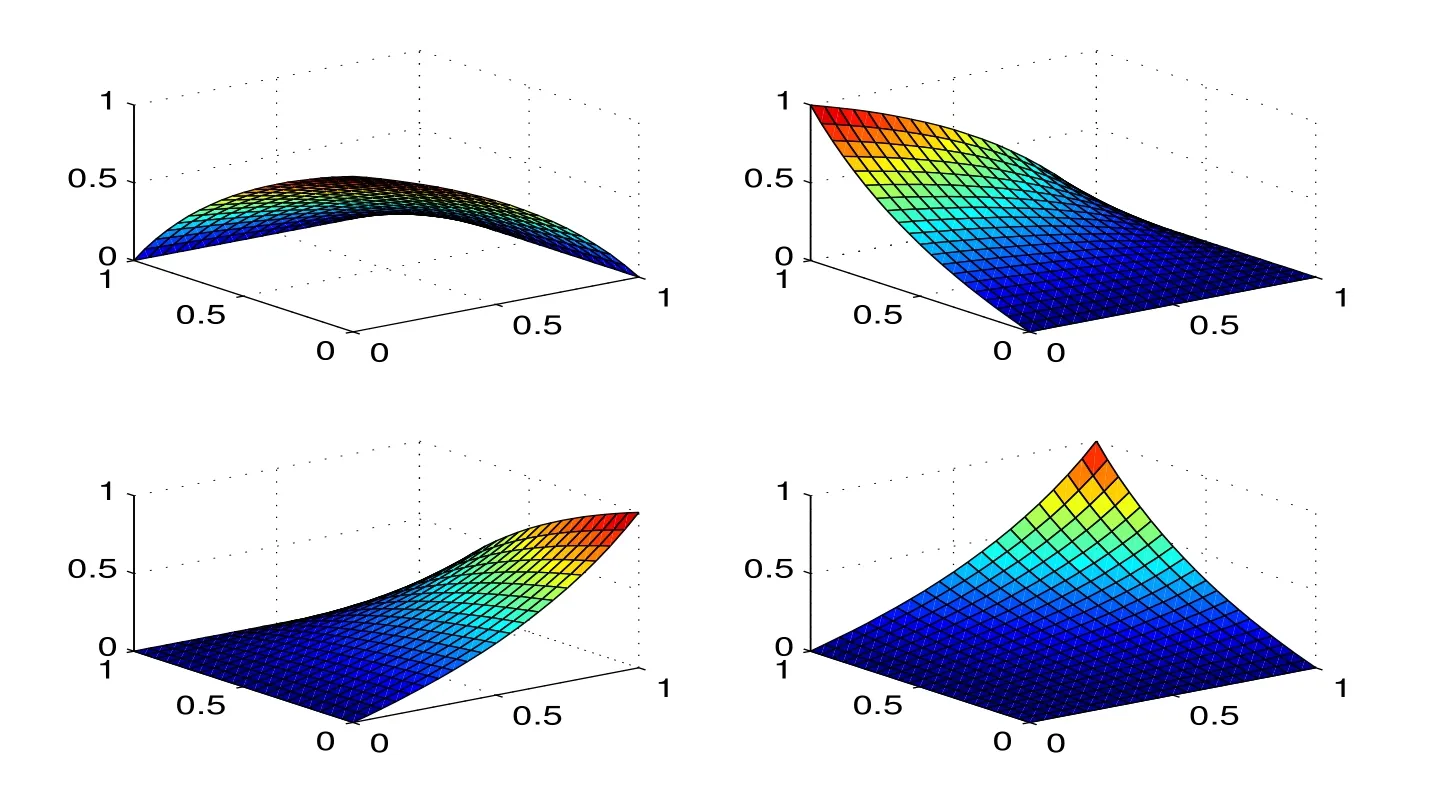
圖1:二元加權有理插值函數的基函數

3 插值函數的性質

本節將討論(3)式或(4)式定義的二元有理線性插值函數的積分性質、有界性質及對插值數據的逼近誤差.

首先,由(4)式易知

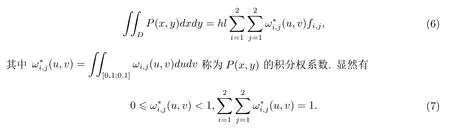
因此當f(x,y)≡1時,由(6)式和(7)式立得如下積分性質.

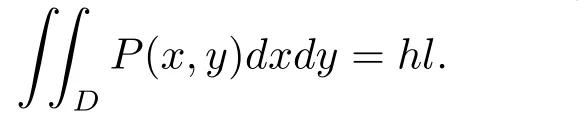
另一方面,利用插值函數的基表示形式,易得加權線性有理插值曲面也具有如下有界性質.

定理 2設{(xi,yj,fi,j)},i=1,2;j=1,2是給定的插值數據點集,α1,α2;β1,β2;λ,μ 是任意正參數,ω∈[0,1].P(x,y)是區域D=[x1,x2;y1,y2]上的加權線性有理插值函數,則

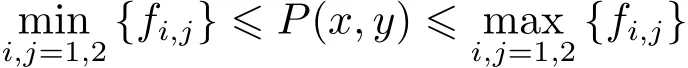
或 |P(x,y)|≤N,其中

利用插值方法構造插值曲面時,插值函數與被插函數的誤差估計是衡量插值方法有效性的一個重要理論依據,如下是關于插值誤差分析的重要結論.

定理 3設{(xi,yj,fi,j)},i=1,2;j=1,2是給定的插值數據點集,α1,α2;β1,β2;λ,μ是任意正參數,ω∈[0,1].若f(x,y)∈C1[x1,x2;y1,y2],則有如下誤差估計

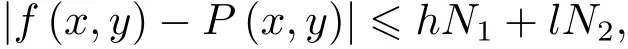
其中N1=max|fx(x,y)|,N2=max|fy(x,y)|.

證對i=1,2;j=1,2,由Taylor展開知

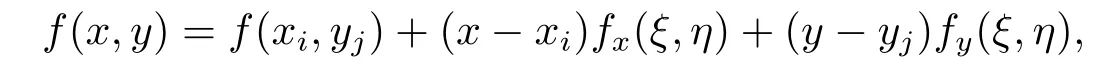
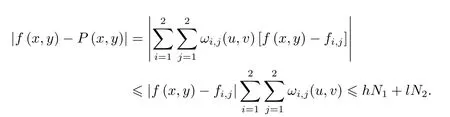
即證.

4 插值曲面的約束形狀控制

插值曲面的形狀控制是幾何設計的一個重要研究方向.一般而言,插值曲面的形狀取決于插值數據,插值數據給定后插值曲面的形狀也就唯一確定了.對于給定的插值數據,本文提出的插值曲面形狀可以靈活調控.

4.1 基于參數的形狀控制

由于本文構造的加權線性有理插值曲面帶有形狀參數和加權系數,插值曲面可以在插值數據給定的前提下,在給定范圍內通過改變參數α1,α2,β1,β2,λ,μ;ω的值可以調控(3)式定義的二元加權有理插值曲面的形狀.

4.1.1 權系數對曲面形狀的整體控制

由插值函數的構造過程可以看出,權系數ω取值整體控制插值曲面的形狀更傾向于極限曲面(x,y)或(x,y).特別的,ω=1或0時P(x,y)分別為(x,y)或(x,y).因此,ω→1時,插值曲面的形狀更傾向于(x,y)的形狀,ω→0時,插值曲面的形狀更傾向于(x,y)的形狀.給定插值數據點集(見表1).

表1:插值數據

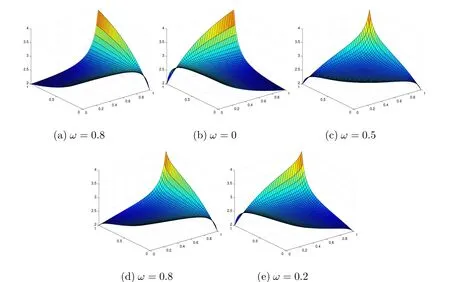
圖2:權系數對插值曲面形狀的影響

取參數α1=α2=β1=β2=6,λ=μ=1,權系數的取值對插值曲面形狀的控制效果如圖2所示.

由圖2可以看出ω=1和ω=0時的曲面(x,y)和(x,y)可視為曲面變化范圍的邊界情形,如圖2(a)(b);ω取值越接近1,曲面的形狀越接近(x,y),如圖2(d);取值越接近0,曲面的形狀越接近(x,y),如圖2(e);而ω=0.5時的曲面兼顧了曲面(x,y)和(x,y)的形狀特點,介于二者之間,如圖2(c).

4.1.2 參數 α1,α2,β1,β2對曲面形狀的局部控制

四個形狀參數α1,α2,β1,β2對曲面形狀的作用類似,故不妨僅討論α1對曲面形狀的局部控制.

注意到在有理插值函數的基表示形式(4)式中,僅ω11(u,v)和ω21(u,v)含有參數α1,且它們滿足

(1)ω11(u,v)是關于α1的增函數;

(2)ω21(u,v)是關于α1的減函數;

(3)ω11(u,v)+ω21(u,v)不再包含α1.

因此,隨著α1的增加,(4)式中f11的權重增加,f21的權重減少,f12和f22的不變.即參數α1主要控制了插值曲面片邊界曲線y=y1(x1≤x≤x2)的形狀.同理,參數α2,β1,β2主要控制了插值曲面片其它三條邊界曲線的形狀.對插值數據點集(表1),取α2=β1=β2=6,λ=μ=1,ω=0.5,參數α1的取值對插值曲面形狀的控制效果如圖3所示.

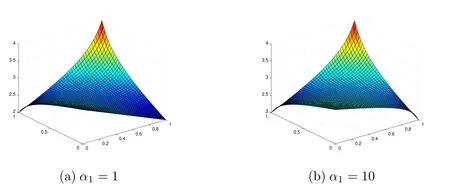
圖3:參數α1對插值曲面形狀的影響.

由于f11＞f21,隨著α1的增大,圖3(a)中α1=1,圖2(c)中α1=6,圖3(b)中α1=10,可以看出邊界曲線y=y1(x1≤x≤x2)上從x1到x2的下降速度變慢,反之則加快.因此參數α1,α2,β1,β2控制了插值曲面片四條邊界曲線的形狀.

4.1.3 參數λ,μ對曲面形狀的局部控制

兩個形狀參數λ,μ對曲面形狀的作用類似,這里僅討論λ對曲面形狀的局部控制.有理插值曲面的基函數中均包含參數λ,且滿足

(1)ω11(u,v)和ω21(u,v)是關于λ的增函數;

(2)ω12(u,v)和ω22(u,v)是關于λ的減函數;

(3) ω11(u,v)+ω12(u,v)+ω21(u,v)+ω22(u,v)=1.

因此隨著λ的增加,(4)式中f11和f21的權重增加,f12和f22的權重減少.即參數λ控制了插值曲面片沿y(x1≤x≤x2)方向的變化趨勢.對插值數據點集(表1),取ω=0.5,α1=α2=β1=β2=6,λ=1,參數μ的取值對插值曲面形狀的控制效果如圖4所示.

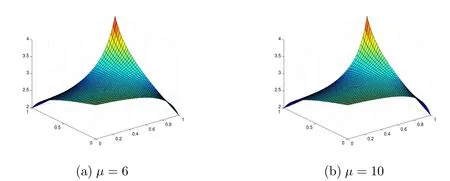
圖4:參數μ對插值曲面形狀的影響.

隨著μ的增大,圖2(c)中μ=1,圖4(a)中μ=6,圖4(b)中μ=10,可以看出越靠近邊界曲線x=x1(y1≤y≤y2)插值曲面越“平緩”,越靠近邊界曲線x=x2(y1≤y≤y2)插值曲面越“陡峭”.因此參數λ,μ分別控制了插值曲面片沿兩個坐標軸方向的變化趨勢.

4.2 函數值約束控制

對于插值區域D=[x1,x2;y1,y2]內的任意點(x,y),令(u,v)為局部坐標.以下定量分析插值曲面的局部點控制問題,即如何確定插值曲面在某點處的函數值等于給定的實數M,其中

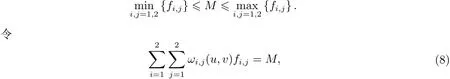
稱(8)式為函數值控制方程.局部坐標(u,v)已知,若能找到一組待定正參數α1,α2,β1,β2,λ,μ和權系數ω滿足(8)式,則可以實現局部函數值約束控制.

不失一般性,上述形狀控制問題可以歸結為中央點函數值控制問題,即此時(u,v)=(0.5,0.5).為了簡化運算步驟,不妨令λ=μ=ω=0.5,α1=α2=α,β1=β2=β,α和β為待定參數.則中央點函數值控制方程可表示為

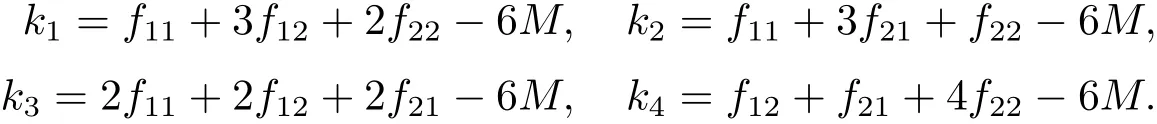
其中因此可以得到如下結論.

定理4加權有理插值函數的中央點函數值控制問題有解的充分條件是序列{k1,k2,k3,k4}變號數的值不為零.

證由函數值控制方程(9)式可知,參數α和β若存在正解,則加權線性有理插值函數的中央點函數值控制問題有解的充分條件是k1,k2,k3,k4不同號,即證.

給定平面區域D=[0,1;0,1],插值數據如表1所示.下面討論加權線性有理插值函數的中央點函數值控制問題.取λ=μ=ω=0.5,α1=α2=α,β1=β2=β.為了便于求解,不妨設α=β.

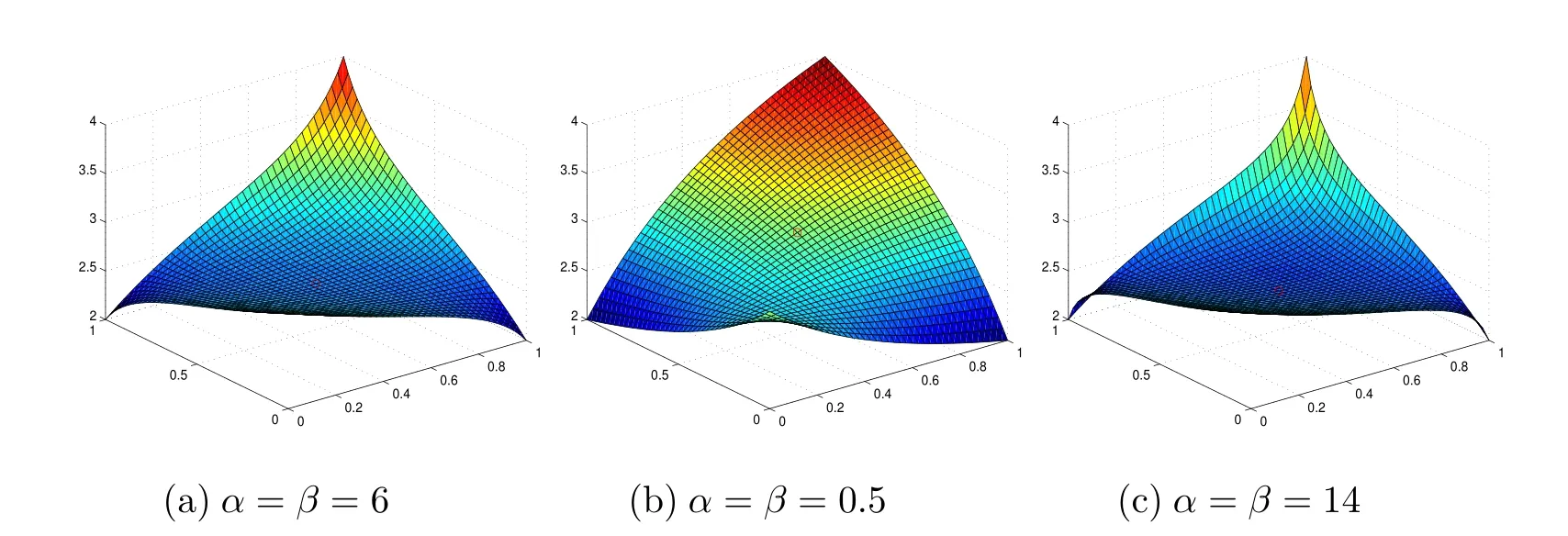
圖5:有理插值曲面的中央點函數值控制.

(1)α=β=6時,中央點函數值M=2.4762,此時的有理插值曲面如圖5(a).

(2)若要使插值曲面在中央點的形狀“上升”,如M=3,根據(9)式只需α=β=0.5,此時的有理插值曲面如圖5(b).

(3)若要使插值曲面在中央點的形狀“下降”,如M=2.4,根據(9)式只需α=β=14,此時的有理插值曲面如圖5(c).

5 結語

本文利用加權組合的方法,先按不同順序生成兩種二元線性有理插值曲面,然后將二者加權組合得到一種新的線性有理插值曲面.該插值曲面具有對稱的基表示形式,滿足積分一致性,有界性,討論了其插值誤差分析.對于給定的插值數據,在一定范圍內改變形狀參數α1,α2,β1,β2,λ,μ和權系數ω的值可以整體或局部調控有理插值曲面的形狀并實現中央點函數值控制.

基函數共包含7個參數,雖然參數多有利于控制形狀,但是也給參數的選擇帶來諸多不便,可考慮適當減少一些不必要或對曲面形狀影響不大的參數.如可令α1=α2,β1=β2,λ=μ,對稱地控制曲面的形狀.數值實驗結果表明,與現有三次及四次有理插值方法相比,線性有理插值方法次數更低,計算量小,形狀控制方法簡單有效.

參考文獻

[1]張慧明,李建俊,段繼光.|x|在調整的第二類Chebyshev結點組的有理插值[J].數學雜志,2014,34(3):509–514.

[2]劉愛奎,段奇,杜世田,曹慶杰,E.H.Twizell.插值曲線區域控制的加權有理插值方法[J].計算機輔助設計與圖形學學報,2000,12(7):497–501.

[3]Ideon E,Oja P.Linear/linear rational spline collocation for linear boundary value problems[J].J.Comp.Appl.Math.,2014,263:32–44.

[4]Han X L.Convexity-preserving approximation by univariate cubic splines[J].J.Comp.Appl.Math.,2015,287:196–206.

[5]Sun Q H,Bao F X,Zhang Y F,Duan Q.A bivariate rational interpolation based on scattered data on parallel lines[J].J.Vis.Commun.Image R.,2013,24:75–80.

[6]Duan Q,Zhang Y F,Twizell E H.A bivariate rational interpolation and the properties[J].Appl.Math.Comp.,2006,179:190–199.

[7]Duan Q,Wang L,Twizell E H.A new bivariate rational interpolation based on function values[J].Infor.Sci.,2004,166:181–191.

[8]Duan Q,Zhang H L,Liu A K,Li H G.A bivariate rational interpolation with a bi-quadratic denominator[J].J.Comp.Appl.Math.,2006,195:24–33.

[9]鄧四清,方逵,謝進.一種新的基于函數值的二元有理插值及其性質[J].應用數學學報,2008,31(4):758–768.

[10]鄧四清,方逵,謝進,陳福來,陸海波.一種基于函數值的二元有理插值函數及其性質[J].計算數學,2009,31(1):77–86.

[11]鄧四清,方逵,謝進,陳福來,陸海波.一種新的帶參數雙三次有理插值樣條的有界性與點控制[J].計算數學,2010,32(4):337–348.

[12]項梅靈,唐月紅.一種二元有理插值樣條函數的凸性[J].計算機輔助設計與圖形學學報,2012,24(9):1171–1179.

[13]Huang W X,Wang G J.A weighted bivariate blending rational interpolation based on function values[J].Appl.Math.Comp.,2011,217:4644–4653.

[14]Zhang Y F,Bao F X,Zhang C M,Duan Q.A weighted bivariate blending rational interpolation function and visualization control[J].J.Comp.Anal.Appl.,2012,14(7):1303–1320.