基于投影尋蹤算法對體型轉變的可能性評價研究

王 涵，黎長春，張 雷

（重慶交通大學，重慶 400074）

《富態：腰圍改變中國》作者認為，“肥胖問題是中國未來經濟發展和公共衛生系統的一枚定時炸彈。”不要讓肥胖大肆地禍害少年兒童。然而，青少年肥胖問題不僅是在中國呈嚴峻趨勢，更是在其他多個國家肆掠，儼然成為全球性的問題。通過比較各個國家中青少年肥胖轉變的可能性，得到普遍的規律以便國家間進行互相學習。

1 問題分析

為了對該群體的轉變可能性進行科學評價，首先需要對影響其轉變可能性的因子進行判定，篩選出最合適且影響度較大的因子，以形成一套完整的可能性指標體系。得到評級體系后，基于投影尋蹤算法建立肥胖轉變可能性評估模型得到5個國家的評價分值。就實際情況將由肥胖轉變為正常體型可能性劃分為5個等級，進而可將5個國家的轉變可能性分等定級。

2 投影尋蹤算法

由美國科學家Kruskal提出的投影尋蹤聚類方法普遍應用于處理和分析高維數據。該方法既可進行不確定分析，也可進行確定性分析，經常用于各種方案的選擇、生態安全中的評價分析、建設條件下的等級評價、可能性的評價以及項目決策分析與評價。因此，本文基于投影尋蹤算法，對肥胖青少年由肥胖向正常體型轉變的可能性進行評價。

3 模型的建立

3.1 指標體系的建立

由肥轉向正常體型的轉變可能性取決于外界因子、人體承受能力和應對能力3個方面。由于在外界因子的干擾下，再加上人體的應對能力的脆弱容易使轉變為正常體型的可能性降低，如果人體在外界因子的干擾下而不采取措施，則會引起肥胖。本文通過查詢相關文獻資料，總結出在青少年肥胖背景下的外界因子、人體承受能力和應對能力3個一級指標，其下包括相對應的8個二級指標，以此建立肥胖轉變為正常體型的可能性指標體系，如圖1所示。

圖1 指標體系

3.2 肥胖轉變可能性評估模型的建立

由于該可能性評估的復雜性與多變性，單一函數不可能準確描述出肥胖轉變為正常體型的可能性與三者之間的關系，因此，本文采用投影尋蹤聚類方法對肥胖轉變為正常體型的可能性進行評價。

3.3 評價指標歸一化處理

假設由肥胖轉為正常體型的可行性指標的樣本集為{x*（i，j），i=1，2，…，n，j=1，2，…，p}，其中，x*（i，j）為第i個樣本的第j個指標值，n和p分別為待評國家數和可能性指標的數目，由于各指標值存在量綱差異，并需要統一其變化范圍。

可采用下式處理越大越優的指標：

可采用下式處理越小越優的指標：

式（1）（2）中：xmax（j）、xmin（j）分別為第 i個指標值的最大值和最小值，x（i，j）為指標特征值歸一化的序列。

3.4 線性投影

線性投影的原理即從不同角度對數據進行分析從而得到數據特征的最優投影方向。因此，本文采用線性投影，將多項影響指標值投影到一維空間上，進而得到反映該國家的特征數值，其被認為是能夠反映該國家的肥胖轉變可能性等級的量化值。將p維數據{x（i，j）│j=1，2，…，p}綜合成以a={a（1），a（2），…，a（p）}為投影方向的一位投影值 z（j），即：

3.5 投影指標函數Q（a）的構建

投影指標散步特征被要求具有局部密集性，而在整體投影點團具有分散性。因此，投影指標函數為：

式（4）中：SZ為投影值z（i）的標準差；DZ為投影值的局部密度。

此外，且：

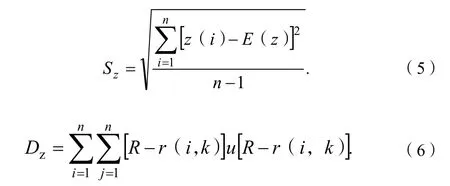
式（5）（6）中：E（z）為序列{z（i）│i=1，2，…，n}的均值；R為局部密度的窗口半徑，通常取值為0.1SZ；r（i，k）=│z（i）－z（k）│，k=1，2，…，n，為樣本之間的距離；u[R－r（i，k）]為以單位階躍函數，當R－r（i，k）≥0時，值為1，當R－r（i，k）＜0時，值為0.綜上所述，目標函數與不同類的樣本離散度（或同類樣本的聚集度）成正比。

3.6 優化投影指標函數

已知最佳投影方向是Q（a）取得最大值時所對應的投影方向，其可表示為這是一個以{a（j）│j=1，2，…，p}為優化變量的復雜非線性優化問題，常用加速遺傳算法（RACA）來處理，本文基于其求解代碼，通過MATLAB實現了該運算。

3.7 評價等級及意義

投影特征值z（i）總體上反映了肥胖轉變可能性的情況，參考相關文獻中的等級劃分原則，本文將其可能性等級分為五個等級（高、較高、中等、較低和低），肥胖轉變可能性等級劃分如表1所示。

表1 肥胖轉變可能性的等級劃分

3.8 綜合評價分析

依據最佳投影方向，可計算待評樣本的投影值z（i）。將計算結果與表1中所列的投影特征值區間進行對照，即可確定肥胖轉變可能性的等級。

4 模型的求解

根據肥胖轉變為正常體型的可能性評價指標體系以及收集到的數據資料，對各個國家的同一影響因素進行排名，根據排名打分，最高為5分，最低為1分。分值越高，其轉變可能性越低；反之越高。

各國家肥胖轉變可能性的評價可根據其分值進行投影尋蹤聚類分析，由于指標分值越高，轉變可能性越低，因此，將以上數據歸一化處理可計算出結果。得到含有未知向量的投影值 z1=0.75a（1）+0.75a（2）+0.75a（3）+0.75a（4）+0a（5）+0.5a（6）+1a（7）+0.75a（8），同理代入第二、三、四組數據可得z2，z3，z4，z5的表達式，將各個表達式代入投影指標函數Q（a）。通過對目標函數及約束函數的編寫，可利用MATLAB中的遺傳算法工具箱進行求解。設置群體大小為100；終止進化代數取200；交叉概率取0.99；變異概率取0.1，可得到最佳投影方向向量a=（0.301 7，0.194 8，0.079 5，0.421 5，0.272 3，0.392 7，0.447 1，0.4805）。將最佳投影方向向量a代入公式得到各個國家的投影特征值z（i）和可能性等級如表2所示。

表2 各國家投影特征值和肥胖轉變可能性等級

5 結果與分析

在基于投影尋蹤聚類的肥胖體型轉變（由肥胖轉變為正常）的可能性評價模型中，最佳投影方向向量中各分量的大小實質上反映的是各指標對肥胖轉變可能性的影響程度。因此，其值越大，對其可能性的影響程度就越大。

評價結果顯示，中國和南非肥胖轉變為正常體型的可能性較高，新西蘭肥胖轉變為正常體型的可能性中等，美國和西班牙肥胖轉變為正常體型的可能性較低。本文對5個國家肥胖轉變為正常體型的可能性評價結果同實際情況的符合度較高，即可驗證該模型的可行性與可靠性。

6 模型的評價與推廣

采用投影尋蹤模型進行可能性評價，即需要將評價指標視為多投影參數的投影方向，從最佳投影值計算出每個國家的肥胖轉變概率，有效地避免了人工賦值權重的干擾。如果加入更多的因素來評價該轉變的可能性，同時，考慮主客觀相結合的方法對評價指標賦值權重，模型將更切合實際。

利用該模型，可對某一地區的肥胖程度進行評估。通過分析肥胖的影響因素，可以根據實際問題控制或降低肥胖的比例，投影尋蹤聚類模型也可有效用于水質安全評價。

參考文獻：

［1］舒暢，姚安林，韓昌柴，等.基于投影尋蹤聚類的油氣管道失效可能性評價［J］.中國安全生產科學技術，2016，12（12）：99-104.

［2］劉海娟.遺傳投影尋蹤模型在生態評價中的應用［D］.蘭州：蘭州大學，2013.

［3］黃顯峰，賈永樂，方國華.基于投影尋蹤法的城市水生態文明建設評價［J］.水資源保護，2016，32（06）：117-122.