精彩的疊合矩形

金 敏

平行四邊形知識(shí)是中考的重點(diǎn)內(nèi)容，該部分試題考查面廣.下面選取其中的一個(gè)考點(diǎn)——平行四邊形中的折疊問題進(jìn)行分析，希望對(duì)同學(xué)們的學(xué)習(xí)有所幫助.

【例題】（2017·浙江金華）如圖1，將△ABC紙片沿中位線EH折疊，使點(diǎn)A的對(duì)稱點(diǎn)D落在BC邊上，再將紙片分別沿等腰△BED和等腰△DHC的底邊上的高線EF，HG折疊，折疊后的三個(gè)三角形拼合形成一個(gè)矩形.類似地，對(duì)多邊形進(jìn)行折疊，若翻折后的圖形恰能拼成一個(gè)無縫隙、無重疊的矩形，這樣的矩形稱為疊合矩形.

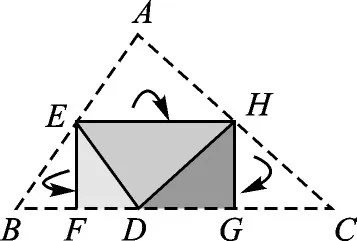
圖1

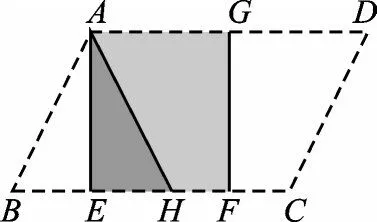
圖2

圖3

圖4

（1）將平行四邊形ABCD紙片按圖2的方式折疊成一個(gè)疊合矩形AEFG，則操作形成的折痕分別是線段_____，___；S矩形EFGA∶S?ABCD=_____.

（2）?ABCD紙片還可以按圖3的方式折疊成一個(gè)疊合矩形EFGH，若EF=5，EH=12，求AD的長.

（3）如圖4，四邊形ABCD紙片滿足AD∥BC，AD＜BC，AB⊥BC，AB=8，CD=10，小明把該紙片折疊，得到疊合正方形.請(qǐng)你幫助畫出疊合正方形的示意圖，并求出AD，BC的長.

【分析】什么是疊合矩形呢？我們結(jié)合題目中的例子來認(rèn)識(shí)一下.在圖1中，我們可以看到△ABC通過翻折形成疊合矩形EFGH的過程.題中“折疊后的三個(gè)三角形拼合形成一個(gè)矩形”指的是△EHD、△HDG、△EDF拼成疊合矩形EFGH.舉例之后，題目給出疊合矩形的定義：若翻折后的圖形恰能拼成一個(gè)無縫隙、無重疊的矩形，這樣的矩形稱為疊合矩形.關(guān)注關(guān)鍵詞的含義，定義中的“無縫隙、無重疊”表明翻折后的圖形的邊是互相重合的.

認(rèn)識(shí)了疊合矩形之后，再解決問題.在問題（1）中，△AHE和梯形HFGA組成了疊合矩形AEFG，它們是通過折疊形成的，所以折痕是AE、GF.由于重合圖形的面積相等，可得S△ABE=S△AHE，S梯形FHAG=S梯形FCDG，所以S矩形AEFG=-

根據(jù)問題（1）中的解題經(jīng)驗(yàn)，對(duì)于問題（2），我們首先要思考疊合矩形是怎么形成的.觀察圖形，不難發(fā)現(xiàn)疊合矩形由四個(gè)三角形“無縫隙、無重疊”拼成，需要折疊四次，EF、EH、HG、FG是折痕.接下來進(jìn)行計(jì)算.從已知出發(fā)，在矩形EFGH中，由 EF=5，EH=12，可得FH=13.從而思考已求的FH與要求的AD之間的關(guān)系.聯(lián)想翻折和矩形的性質(zhì)，可以得到△AEH≌△MEH≌△CGF≌△NGF，△DHG≌△NHG≌△BFE≌△MFE，所以DH=HN，CF=FN=AH，所以 FN+NH=AH+DH，即FH=AD.

問題（3）主要是設(shè)計(jì)折疊方案.同樣需要借助解決前兩個(gè)問題的經(jīng)驗(yàn)尋找解題的思路.一方面，如圖5（1）所示，梯形ABCD由△DEC和矩形ABED組成.矩形ABED沿邊AB和DE的中點(diǎn)連線對(duì)折就可以得到疊合矩形；△DEC按圖1的方法折疊也可以得到疊合矩形.綜合這兩個(gè)圖形的翻折方式，可以獲得梯形中的疊合矩形.另一方面，矩形是特殊的平行四邊形，可以根據(jù)圖3的方法得到疊合矩形.因此可以借助圖3的翻折方法來理解圖4中四邊形的折疊，分成兩類：一類是沿∠A、∠B、∠C所在的區(qū)域折疊，如圖5（2）所示（虛線是折痕）.另一類是沿∠A、∠B、∠C、∠D所在的區(qū)域折疊，如圖5（3）所示.

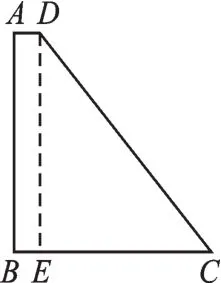
圖5（1）

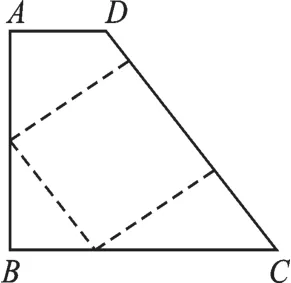
圖5（2）

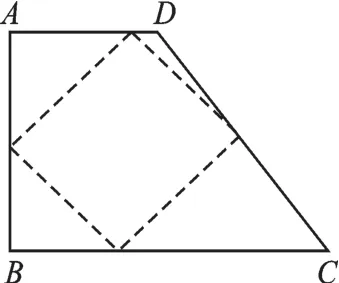
圖5（3）

【解】（1）AE、GF，）AD=13；（3）有三種折法：如圖6（1）、圖6（2）、圖6（3）所示.

第一種：如圖6（1），EF、FG是折痕，則AE=EB=AB=4，DF=FC=FH=CD=5.∵四邊形EBGF是正方形，∴FG=EB=4，∠FGH=90°.∴在Rt△FHG中，HG==3.∴CH=2HG=6，BH=BGHG=1.∴AD=1，BC=7.

CF=NF.∴HG==5.在 Rt△EBF 中 ，BF=AD=BC-6=

第三種：如圖6（3），EF、FG、GH、EH是折痕，則AE=AH=BF=BE=AB=4；DH=HM，CF=MF.∴CF+DH=FH=8.易得CF-DH=6，∴CF=7，DH=1.則AD=5，BC=11.

圖6（1）

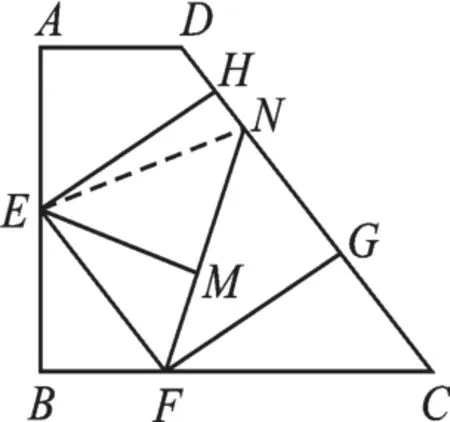
圖6（2）

圖6（3）

【點(diǎn)評(píng)】這是一道基于閱讀理解的探索題.根據(jù)題目，正確理解“疊合矩形”的定義是解決問題的前提.問題（3）是本題的難點(diǎn)，其解決需要經(jīng)歷以下過程：大致想象疊合后的正方形的位置，準(zhǔn)確推理折疊方式，然后精確計(jì)算未知線段的長度.其中，想象和畫出疊合正方形是解決問題的關(guān)鍵.借助問題（1）和問題（2）的經(jīng)驗(yàn)，使用轉(zhuǎn)化策略是解決問題（3）的方法.同時(shí)，還需要注意，翻折的方法不唯一，需要分類討論；計(jì)算線段長度時(shí)需要利用重合圖形全等的性質(zhì).

【拓展】矩形和菱形都是特殊的平行四邊形，任意的矩形都可以按照?qǐng)D2和圖3的方法折成疊合矩形.任意的菱形是否也可以這樣折呢？

【分析】我們同樣需要分類考慮，在菱形ABCD中，不妨設(shè)∠B是銳角.當(dāng)60°≤∠B＜90°時(shí)，可以按照?qǐng)D2和圖3的方法折疊，分別是圖7（1）中的矩形AEFG、圖7（2）中的矩形EHFG.當(dāng)0°＜∠B＜60°時(shí)，按圖7（1）的方式不能形成矩形，只有圖7（2）的方法可以.

圖 7（1）

圖 7（2）