大跨度橋梁PK箱梁斷面顫振性能研究

方根深, 楊詠昕, 葛耀君

(同濟大學 土木工程防災國家重點實驗室,上海 200092)

為了適應跨江跨海等工程需求，現代橋梁結構在設計理論、施工技術逐漸成熟的保證下，向跨度更大、體系更柔的方向發展，同時鋼材的廣泛使用，又使結構自重減輕、阻尼降低。這必然導致結構對風的敏感性增加，特別是1940年老Tacoma橋的風毀事故引起了工程界對結構抗風的高度重視，風振可靠度驗證成為了大跨度橋梁結構設計的關鍵環節。顫振是一種氣體與彈性結構相互作用的氣動彈性現象，一旦發生將會對橋梁結構造成災難性的破壞。因此，研究大跨度橋梁的顫振性能是長期安全使用的重要保證。目前針對大跨度橋梁的顫振穩定性已經有了較為系統的研究[1-3]。而對于顫振發生的物理解釋，特別是不同橋梁斷面帶來的顯著差異以及各氣動措施的作用機理，還有待進一步探討和完善。Matsumoto等[4]采用分步分析(step by step)的方法，將顫振分析分為扭轉和豎彎兩個運動分支，研究了顫振發展過程中系統阻尼、剛度的變化，初步解釋了顫振發生機理。Yang等[5-6]進一步分析了顫振臨界狀態各自由度的參與程度，同時解釋了部分結構措施和氣動控制措施的作用機制。

PK箱梁斷面最早源于美國Pasco-Kennewick橋[7]，該橋首次采用了雙邊三角形箱梁的主梁形式，此后工程界將這種半開口分離雙箱斷面簡稱為PK斷面，在近幾年越來越多的被運用到實際工程中，特別是寬主梁雙索面密索體系大跨徑斜拉橋，如鄂東長江大橋、荊岳長江大橋等。PK斷面主梁橫向剛度較大，而且相比于閉口箱梁可以節省下底板的材料用量，同時在氣動性能方面整體表現良好。已有研究表明，PK箱梁斷面主要存在+3°或+5°風攻角的大幅豎彎渦振現象[8-10]，同時根據風洞試驗提出了抑流板這一有效控制措施[11]，而抑流板對顫振性能的影響有待研究。與此同時，在荊岳長江大橋的全橋氣彈風洞試驗中還發現，成橋狀態下，-3°風攻角時顫振安全儲備充足，而+3°風攻角時臨界風速(實橋56 m/s)比0°(實橋98.4 m/s)低了43%；孟曉亮等[12]對70°風嘴椒江二橋的試驗中也發現成橋運營狀態的+3°風攻角顫振臨界風速(114 m/s)比0°時(200 m/s)也要低43%，有必要對這種風攻角高敏感性作出解釋；朱樂東等[13]發現PK箱梁斷面橋梁存在復雜的軟顫振現象，在不同風速和風攻角下，會有軟顫振需要初始激勵、大振幅激勵發散、小振幅激勵衰減、軟顫振之后緩慢發散四種現象，同時其試驗結果表明+3°和+5°風攻角顫振臨界風速基本不變，但是比0°風攻角小了接近75%。可見，PK斷面顫振性能復雜，一方面需要在對不同風攻角下復雜的顫振現象有了定性認識的基礎上，能夠解釋風攻角敏感性問題，另一方面希望能夠尋找合適氣動措施，在提高正風攻角下氣動失穩臨界風速的基礎上，對渦振控制也能起到有利作用，以期PK斷面在山區存在大風攻角以及沿海高設計風速地帶能有更廣闊的發展空間。

目前關于PK箱梁斷面顫振性能較完整的研究較少，本文以某大跨度混合梁斜拉橋為研究背景，以成橋狀態的PK斷面為基本斷面，進行了節段剛體模型風洞試驗，并結合理論分析，研究了其顫振穩定性能。在此基礎上，探討了抑流板對其顫振性能的影響，為該種斷面的廣泛使用所需要的抗風設計提供參考。

1 風洞試驗與顫振性能

1.1 基本斷面與風洞試驗

PK箱梁斷面寬38.5 m，高3.425～3.8 m，橋面坡度2%，底板開口寬度13.9 m，橫隔板設置間距為3 m，如圖1所示。本文設計了幾何縮尺比例λL=1∶70的剛體節段模型，選用彈簧懸掛二元剛體節段模型方法進行顫振試驗，在滿足幾何外形相似基礎上，保持彈性參數(頻率比)、慣性參數(慣性半徑比)、阻尼參數(阻尼比)相似，各參數取值見表1。

表1 顫振節段模型風洞試驗主要參數

試驗在同濟大學TJ-2大氣邊界層風洞中進行，選用四個通道高精度激光位移傳感器進行振動信號采集。動力特性和顫振導數的測試采用自由振動法，并通過修正最小二乘法識別顫振導數[14]。PK箱梁斷面實橋外形尺寸與節段模型風洞試驗布置分別見圖1和圖2。

圖1 PK箱梁橫斷面圖(單位:mm)

圖2 彈簧懸掛節段模型風洞試驗與測量儀器

Fig.2 Spring-suspended sectional model system and measuring instrument

1.2 顫振性能

顫振臨界風速是評價橋梁結構顫振性能的關鍵指標，同時關注顫振發展的過程，即結構隨風速增長各動力參數變化過程是認識顫振現象的重要途徑。因此，本文重點關注顫振臨界風速、顫振形態以及阻尼比、顫振導數等隨風速增大的變化情況。

1.2.1 原斷面顫振性能

如圖3和圖4所示，RMS(Root Mean Square)為均方根值，在一定風速范圍內，成橋狀態的PK斷面存在著較穩定的扭轉振動，且振幅隨風速增大而增大，即為 “軟顫振”現象，是一種單模態的、由自激力非線性引起的結構自平衡狀態[15]，由于氣動偏心(扭轉中心往來流上游側偏移)作用表現為彎扭自由度耦合的振動形態。

圖3 +3°風攻角下“軟顫振”現象(實橋風速64.35 m/s)

Fig.3 “Soft flutter” phenomenon at attack angle of +3°(wind speed is 64.35 m/s)

圖4 原始斷面不同風攻角下扭轉角根方差

從圖4～圖6可以看出，PK箱梁斷面在+3°風攻角下較低風速就表現出顫振特點，而0°風攻角顫振風速提高接近了一倍，-3°風攻角則在試驗風速下未發生顫振現象。在進入“軟顫振”風速區間時，系統阻尼比趨于0，大振幅激勵下會逐漸衰減到穩定振幅。

圖5 原始斷面不同風攻角下扭轉響應峰值因子

Fig.5 Peak factor of torsional angle at different attack angles of original section

1.2.2 抑流板對顫振性能的影響

朱樂東等研究表明典型橋梁斷面的“軟顫振”有別于傳統的“硬顫振”，其臨界風速很難通過改變結構阻尼比或者橋面附屬結構大幅度提高。本文在風洞試驗中，發現抑流板能夠在有效抑制PK箱梁斷面渦振的基礎上，大幅度提高其在+3°風攻角下的顫振臨界風速，對0°和-3°風攻角的臨界風速影響較小，能夠有效達到工程需求目標。因此，對抑流板這一有效氣動措施進行了+3°風攻角下較為細致的研究。

圖6 原始斷面不同風攻角下扭轉阻尼比

Fig.6 Damping ratio for torsional motion at different attack angles of original section

抑流板設計如圖1所示，安裝在最外側檢修道欄桿頂部，與水平夾角15°，并進行了三種寬度尺寸的比較，與檢修道欄桿高度比值分別為η=0.57,η=1.14,η=1.71。圖7～圖9為+3°風攻角下原斷面與安裝了抑流板后主梁響應特征，可以看出，添加抑流板能夠較大幅度提高顫振起振風速；隨著板寬的增大，起振風速有增大的趨勢，但逐漸表現出了“硬顫振”的特點，特別是η=1.71的抑流板，當實橋風速U=83.76 m/s時，在自由振動和一定激勵作用下，扭轉角度都會大幅增加。

1.2.3 顫振臨界風速

由于對“軟顫振”的風速臨界點沒有較明確的規定，本文基于性能設計的思想，采用了扭轉角根方差大于0.5°、峰值因子PF值小于2以及系統阻尼比等于0的綜合評定方法，取對應的最小風速為顫振臨界風速。表2給出了以上各工況對應的臨界風速。

圖7 +3°風攻角下扭轉角根方差

圖8 +3°風攻角下扭轉阻尼比

Fig.8 Damping ratio for torsional motion at attack angle of +3°

圖9 +3°風攻角下扭轉峰值因子

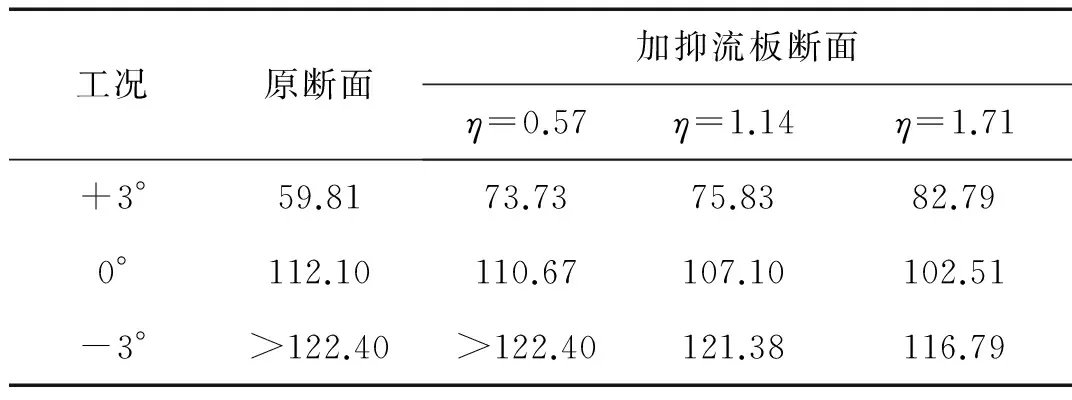
工況原斷面加抑流板斷面η=0.57η=1.14η=1.71+3°59.8173.7375.8382.790°112.10110.67107.10102.51-3°>122.40>122.40121.38116.79

可以看出，原斷面+3°風攻角下臨界風速較低，比0°風攻角下低了46.6%，表現出顯著的風攻角效應；抑流板可以有效提高+3°風攻角下的臨界風速，增大幅度隨板寬增大而呈現增大趨勢，η=0.57,η=1.14和η=1.71時，臨界風速分別增大23.3%,26.8%,38.4%。同時，試驗中也進行了抑流板對0°和-3°風攻角顫振影響的研究，其臨界風速有減小的趨勢，但是在試驗工況范圍內減小的幅度不大，且此時臨界風速仍然遠大于+3°風攻角下的結果。

1.2.4 顫振導數

2 顫振驅動機理解釋

雖然“軟顫振”是由自激力的非線性效應引起的，但基于Scanlan頻域線性顫振理論，可以建立能同時研究二維橋梁節段模型扭轉、豎向和側向振動參數(系統阻尼及系統剛度)，與氣動外形參數(氣動導數)的定量關系，從而清晰的認識顫振發展過程中的結構系統剛度、阻尼的變化，解釋顫振驅動機理。因此，本文從頻域角度對PK箱梁斷面顫振的攻角效應和抑流板的作用機理作出解釋。

2.1 二維三自由度(2D-3DOF)顫振分析理論

基于Scanlan在頻域的線性顫振理論，定義主梁運動的三個主要自由度為x={p,h,α}T；可以將二維三自由度的運動方程寫為

(a)顫振導數

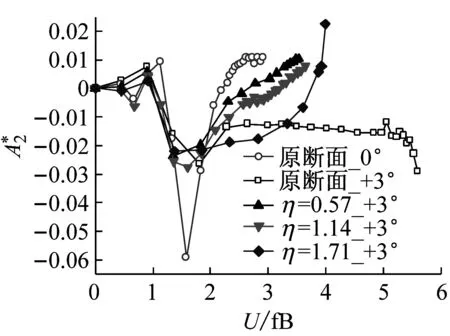
(b)顫振導數

(c)顫振導數

(1)

式中:M={mp,mh,Iα}、C0={cp,ch,cα}和K0={kp,kh,kα}分別為三個自由度的廣義質量、廣義阻尼和廣義剛度;Cae和Kae分別為氣動阻尼矩陣和氣動剛度矩陣;Fb為抖振力(強迫力)。

Matsumoto等、Yang等和Ge等通過引入不同自由度運動之間的激勵-反饋機制來解耦顫振運動方程組，從而對系統扭轉牽連運動、豎向牽連運動和側向牽連運動進行求解。下面僅考慮豎向和扭轉兩個自由度，扭轉牽連運動方程可以表達為

(2)

式中:ξα0和ωα0分別為扭轉牽連運動的結構阻尼比和固有圓頻率，等號右邊三項分別表示扭轉運動自身產生的氣動力、扭轉速度項耦合豎向運動產生的氣動力以及扭轉位移項耦合豎向運動產生的氣動力，分別為

(3)

表3 扭轉牽連運動氣動剛度與氣動阻尼比

(6)

式中:第一個量描述了耦合豎向運動的參與程度;第二個量則描述了扭轉主運動的參與程度，該矢量在平面幾何坐標單位圓上的位置可以直觀反映相對參與程度。

2.2 原始斷面顫振的顯著攻角效應

由于-3°攻角在試驗風速內未出現顫振現象，此處僅討論0°攻角與+3°攻角顫振性能的顯著差異。0°攻角、+3°攻角氣動阻尼比和系統阻尼比變化規律如圖11和圖12所示。可以看到，0°攻角時，AD_A項和AD_D項起控制作用，其他氣動阻尼項作用甚微；AD_A項即由扭轉運動自身產生的氣動阻尼為正值，且隨風速先逐漸增大后小幅降低，而后緩慢增大逐漸趨于穩定，對系統氣動穩定性起到有利作用；而由扭轉主運動的位移項所產生的耦合氣動升力激發起的耦合豎向運動，其速度所產生的氣動升力矩反饋到扭轉主運動，這一激勵-反饋作用主線表現在AD_D項，其在風速達到一定數值時隨風速增大逐漸減小，對系統穩定性起到不利作用；以上氣動阻尼項與系統機械阻尼比之和等于0時，系統趨于發散，此時風速為102.15 m/s，比試驗風速低了8.9%。+3°攻角時，AD_A項起主要控制作用，其他四項氣動阻尼影響很小；AD_A項隨風速增大先迅速增大，在達到峰值后又迅速減小并變為負值，逐漸抵消系統機械阻尼比而驅動系統發散，此時風速為62.82 m/s，比試驗風速高了5%。

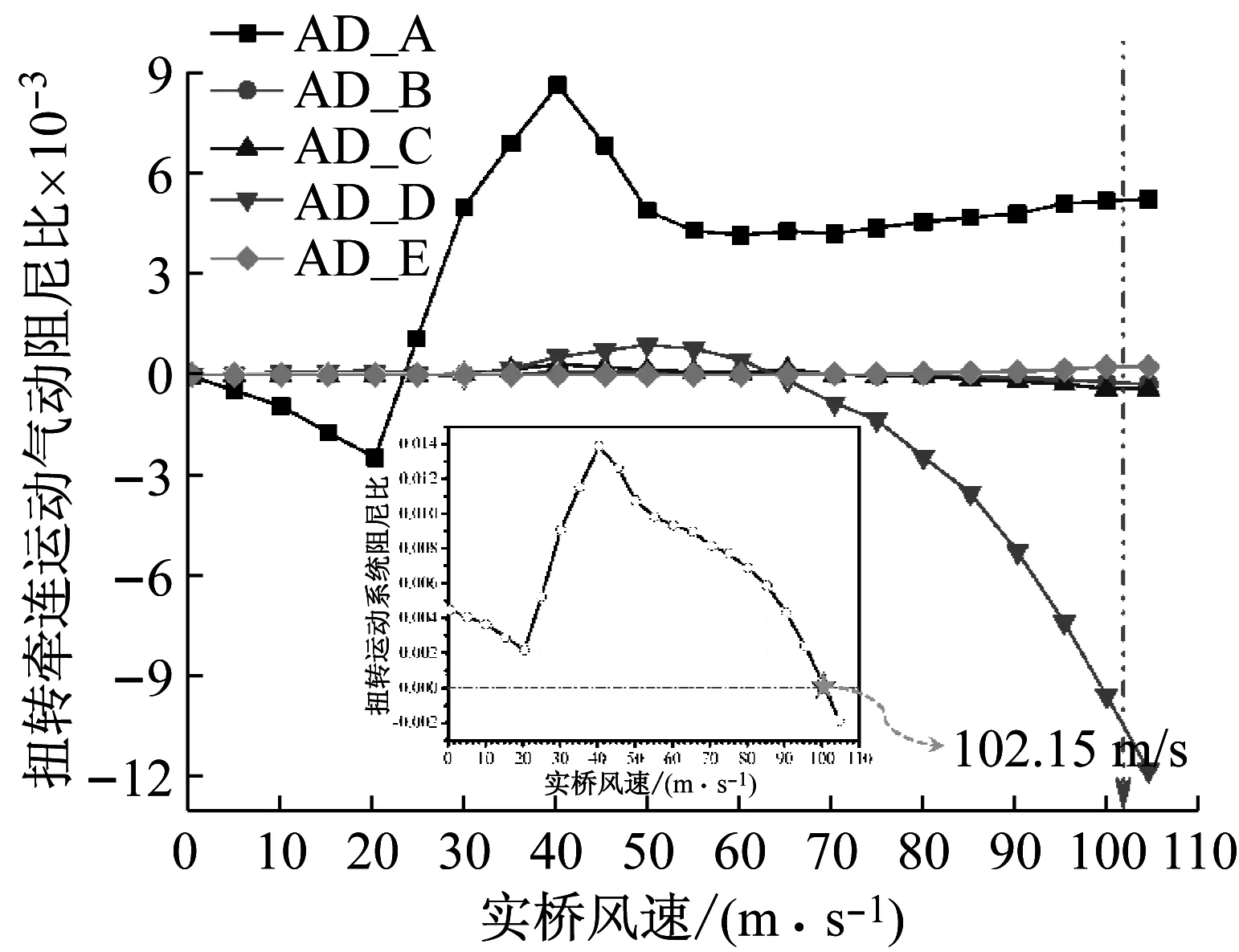
圖11 原始斷面0°風攻角下氣動阻尼比變化規律

Fig.11 Aerodynamic damping ratio of original section at attack angle of 0°

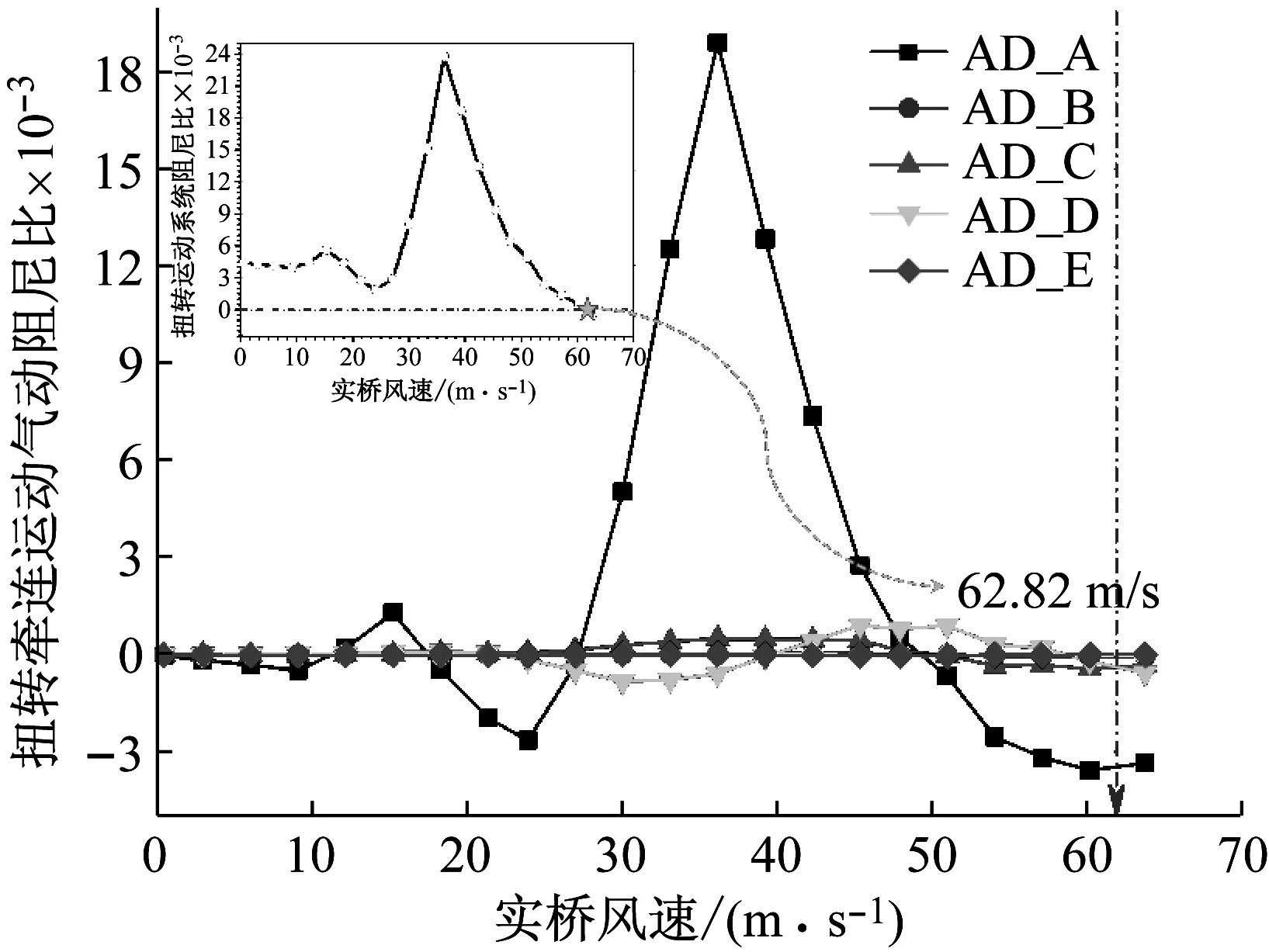
圖12 原始斷面+3°風攻角下氣動阻尼比變化規律

Fig.12 Aerodynamic damping ratio of original section at attack angle of +3°

比較兩個攻角氣動阻尼可以發現，0°攻角下系統表現為明顯的“彎扭耦合顫振”，耦合運動的氣動負阻尼是驅動系統發散的主要原因，但是扭轉運動自身氣動阻尼對系統穩定作用明顯，并隨風速增大有緩慢的增強；而+3°攻角下系統表現為典型的“單自由度扭轉顫振”，耦合作用很微弱，扭轉運動自身產生的氣動阻尼變化劇烈，由正轉負過程迅速，主導了系統的發散。因此，兩個攻角下顫振性能差異顯著，+3°攻角顫振臨界風速也會比0°攻角小很多。

2.3 抑流板顫振作用機理

抑流板對PK斷面+3°攻角的顫振性能起到有效的改善作用，其氣動阻尼比與風速變化關系如圖13所示。可以看出，添加了抑流板后，相比于圖12，系統在高風速雖然耦合氣動負阻尼項逐漸表現出來，但是扭轉運動自身產生的氣動阻尼項減小速度變緩，并與負阻尼相互競爭，而提高了系統的顫振臨界風速。隨著板寬的增大，系統耦合氣動阻尼比AD_D項都會在風速約為55 m/s時隨風速增大而逐漸減小，而AD_C項(即由扭轉主運動的速度項所產生的耦合氣動升力激發起的耦合豎向運動，其位移所產生的氣動升力矩反饋到扭轉主運動的阻尼項)也逐漸表現出不利作用，由此可見，板寬越大，高風速下耦合氣動阻尼的不利作用將越發明顯；但是AD_A項的減小速率也很快放緩，顯然，抑流板對本文中的PK箱梁斷面是有利的，在一定風速范圍內，使得AD_A項在氣動阻尼的競爭中占主導地位從而提高了顫振臨界風速。然而，對于抑流板的控制作用需要進一步結合橋梁斷面表面壓強以及氣流形態等進行比較，其對不同外形PK箱梁斷面顫振性能提升的有效性以及普適性有待進一步結合風洞試驗確定。

2.4 自由度耦合程度

橋梁斷面達到顫振臨界狀態時，扭轉和彎曲兩個自由度的耦合程度可以從顫振形態矢量反映出來(見式(6))，如圖14所示，半徑大小代表了顫振臨界狀態的風速，矢量坐標點橫縱坐標的相對大小代表了豎彎和扭轉自由度的參與程度。可以看出，PK箱梁斷面整體上的顫振耦合程度較弱，原斷面+3°攻角豎向自由度參與程度很低，可以看作是“單自由度扭轉顫振”，而0°攻角雖然仍以扭轉自由度為主，但豎向自由度參與程度有所增大，即表現出耦合顫振特點；添加抑流板的斷面顫振形態矢量在兩者之間，而不同板寬對顫振形態影響不大。

(a) η=0.57

(b) η=1.14

(c) η=1.71

圖14 各斷面顫振形態矢量圖

3 結 論

本文借助風洞試驗并結合理論分析，進行了PK箱梁斷面顫振性能研究，并對三種尺寸抑流板顫振控制效果與機理進行探索，得到以下主要結論：

(1)PK箱梁斷面成橋狀態具有“軟顫振”特點，參考性能設計方法，本文提出扭轉角度根方差大于0.5°、扭轉響應峰值因子小于2以及阻尼比小于0來綜合評定顫振臨界風速。

(2)PK箱梁斷面顫振性能具有顯著的攻角效應，即0°和±3°攻角下顫振臨界風速差異明顯，主要是由于0°攻角時，系統表現出耦合顫振特點，扭轉運動自身產生的氣動阻尼對系統有很強的穩定作用，耦合氣動負阻尼逐漸驅動系統發散；+3°攻角時，系統表現出單自由度扭轉顫振特點，扭轉運動自身產生的氣動阻尼變化劇烈，迅速由正轉負，主導系統顫振發散，而耦合氣動阻尼基本不起作用。

(3)抑流板能有效提高PK箱梁斷面+3°攻角的顫振臨界風速，相比于原斷面，其會在高風速激起耦合氣動負阻尼，而且板寬增大，AD_C項和AD_D項都表現出較大不利作用，然而扭轉運動自身產生的氣動阻尼AD_A項由正轉負的速率變得緩慢，有利于系統的持續穩定，以上兩方面氣動阻尼的競爭將決定系統最終的發散。

(4)PK箱梁斷面整體上的顫振耦合程度較弱，原斷面+3°攻角豎向自由度參與程度很低，可以看作是“單自由度扭轉顫振”，而0°攻角雖然仍以扭轉自由度為主，但豎向自由度參與程度有所增大，即表現出耦合顫振特點；添加抑流板的斷面顫振形態矢量在兩者之間，而不同板寬對顫振形態影響不大。

參 考 文 獻

[1] SIMIU E, SCANLAN R H. Wind effects on structures-fundamentals and applications to design[M]. 3rd ed. New York: John Wiley & Sons, 1996.

[2] 項海帆. 現代橋梁抗風理論與實踐[M]. 北京: 人民交通出版社, 2005.

[3] 葛耀君. 大跨度懸索橋抗風[M]. 北京: 人民交通出版社, 2011.

[4] MATSUMOTO M, DAITO Y, YOSHIZUMI F, et al. Torsional flutter of bluff bodies[J]. Journal of Wind Engineering and Industrial Aerodynamics, 1997, 69/70/71: 871-882.

[5] YANG Y X, GE Y J, XIANG H F. Investigation on flutter mechanism of long-span bridges with 2d-3DOF method[J]. Wind and Structures, 2007, 10(5): 421-435.

[6] GE Y J, ZOU X J, YANG Y X. Aerodynamic stabilization of central stabilizers for box girder suspension bridges[J]. Wind and Structures, 2009, 12(4): 285-298.

[7] GIMSING N J, GEORGAKIS C T. Cable supported bridges-concept and design[M]. 3rd ed. New York: John Wiley & Sons, 2012.

[8] 王騎, 陶奇, 廖海黎, 等. 鄂東大橋主梁大尺度節段模型渦激振動特性試驗研究[C]∥第十三屆全國結構風工程學術會議論文集. 大連: 人民交通出版社, 2007.

[9] 朱樂東, 張海, 張宏杰. 多孔擾流板對半封閉窄箱梁渦振的減振效果[J]. 實驗流體力學, 2012, 26(3): 50-55.

ZHU Ledong, ZHANG Hai, ZHANG Hongjie. Mitigation effect of multi-orifice flow-disturbing plate on vortex-induced resonance of narrow semi-closed box deck[J]. Journal of Experiments in Fluid Mechanics, 2012, 26(3): 50-55.

[10] 宋錦忠, 丁望星, 丁泉順, 等. 湖北荊岳長江公路大橋抗風性能試驗研究[C]∥第十四屆全國結構風工程學術會議. 北京:第十四屆全國結構風工程學術會議論文集, 2009.

[11] 方根深，楊詠昕，葛耀君，等. 半開口分離雙箱梁渦振性能及其氣動控制措施研究[J]. 土木工程學報,2017,50(3):74-82.

FANG Genshen, YANG Yongxin, GE Yaojun, et al. Vortex-induced vibration performance and aerodynamic counter measures of semi-open separated twin-box deck[J]. China Civil Engineering Journal, 2017,50(3):74-82.

[12] 孟曉亮，郭震山, 丁泉順, 等. 風嘴角度對封閉和半封閉箱梁渦振及顫振性能的影響[J]. 工程力學, 2011, 28(增刊1): 184-194.

MENG Xiaoliang, GUO Zhenshan, DING Quanshun, et al. Influence of wind faring angle on vortex-induced vibrations and flutter performances of closed and semi-closed box decks[J]. Engineering Mechanics, 2011, 28(Sup1): 184-194.

[13] 朱樂東，高廣中. 典型橋梁斷面軟顫振現象及影響因素[J]. 同濟大學學報(自然科學版), 2015, 43(9): 1289-1294.

ZHU Ledong, GAO Guangzhong. Influential factors of soft flutter phenomenon for typical bridge deck sections[J]. Journal of Tongji University(Natural Science), 2015, 43(9): 1289-1294.

[14] DING Quanshun, ZHOU Zhiyong, ZHU Ledong, et al. Identification of flutter derivatives of bridge decks with free vibration technique[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2010,98(12): 911-918.

[15] 張朝貴. 橋梁主梁“軟”顫振及其非線性自激氣動力參數識別[D]. 上海: 同濟大學, 2007.

[16] 公路橋梁抗風設計規范:JTG/TD 60-01—2014[S]. 北京: 人民交通出版社, 2004.