煤粉在水平管道輸送過程中的數值模擬
郭培紅, 李 博, 朱建安,, 劉明志, 王 帥
(1.河南理工大學 機械與動力工程學院,河南 焦作 454003;2.焦作市豐創冶金機械有限公司,河南 焦作 454000)
0 引言
在煉鎂回轉窯煤粉制備與噴燒系統中,煤粉的輸送是一個很重要的過程。當煤粉從螺旋泵送出后,通過羅茨風機經管道輸送到燃燒器中的煤粉通道,再通過煤粉通道噴吹到回轉窯中燃燒。其中,從羅茨風機到燃燒器這一段涉及到煤粉在水平管道內輸送問題,屬于氣固兩相流。因為煤風速度過高,管路阻力增大,能耗和磨損都會增大;煤風速度過低,不能形成氣力輸送,導致煤粉在管道內沉積,影響燃燒器噴燒效果。因此對煤粉在水平管道中氣固兩相流進行數值模擬分析,確定合適的煤風速度是十分必要的。
本文利用流體動力學數值計算CFD技術和流體力學的基本數學方程組,通過Fluent前處理軟件Gambit進行三維建模和網格劃分,采用標準k-ε湍流模型和SIMPLE算法對煤粉在水平管道中的輸送過程進行數值模擬,并通過模擬不同的煤風速度,對其進行對比,分析煤風速度對煤粉在水平管道中輸送狀態的影響。
1 基本方程
1.1 氣固兩相流基本方程
本文模擬煤粉在水平管道中的輸送過程,不考慮溫度或者能量,因此不涉及能量方程,只用到質量守恒方程和動量守恒方程[1]。
1)質量守恒方程:

式中:t為時間;ρ為密度;u、v、w分別為x、y、z方向的速度分量。
2)動量守恒方程:
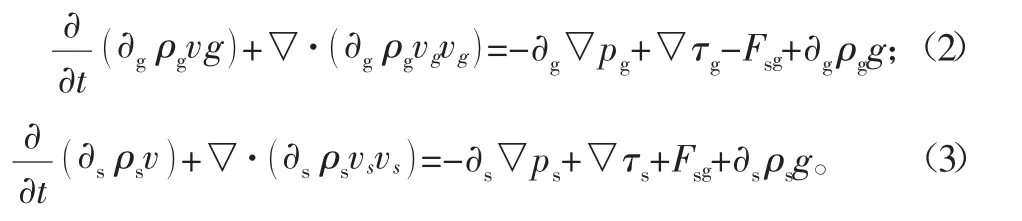
式中:?g、?s分別為氣相和固相的體積分數;ρg、ρs分別為氣相和固相的密度;vg、vs分別為氣相和固相的速度矢量;τg、τs分別為氣相和固相的應力張量;pg為氣相壓力;Fsg為氣固兩相間的作用力;g為重力加速度。
1.2 雙流體模型
目前,對氣固兩相流數值模擬的研究通常使用歐拉-拉格朗日法和雙歐拉法。歐拉-拉格朗日法是對流場中每一個顆粒的運動進行跟蹤,能精確考慮顆粒與顆粒、顆粒與載氣、顆粒與壁面的相互作用,可用于解決離散相和流體組成的兩相流體系,但其計算量較大。雙歐拉法是把不同相之間在數學上被當作互相滲透的連續體,包括把分散的顆粒和流體均看作連續介質,認為顆粒和流體是互相滲透的,可用來模擬彌散相濃度比較高的場合[2]。模型假設各相體積份額為空間和時間的連續函數,各相體積份額之和等于1。
根據本文所要研究的是煤粉在水平管道中輸送問題,不僅要考慮煤粉與空氣之間的相互作用,還要考慮煤粉與煤粉之間的相互作用,因此雙流體模型采用歐拉-歐拉法。
連續方程:

式中:ρk為k相顆粒的表觀密度,ρk=nkmk;nk、mk分別為第k種顆粒的數密度和單個顆粒質量;Fk,Mi為第k種顆粒的Magnus力。
1.3 湍流模型
雙流體模型選用歐拉-歐拉方法進行數值模擬,但還需選用合適的湍流模型予以補充[3-4]。最簡單的完整湍流模型就是兩方程模型中的標準k-ε模型。標準k-ε模型主要針對完全湍流的流動過程模擬,是一種高雷諾數湍流計算模型[5],計算結果可靠,比較常用,因此本模擬采用標準k-ε雙方程湍流模型。
標準k-ε的計算方程為:


式中:Gk為由于平均速度梯度引起的湍動能產生;Gb為由于浮力影響引起的湍動能產生;Ym為可壓縮湍流脈動膨脹對總的耗散率的影響;C1ε、C2ε、C3ε為經驗常數,通常取C1ε=1.44、C2ε=1.92、C3ε=0,09;σk為湍動能對應的普朗特數,σk=1.0;σε為湍動耗散率對應的普朗特數,通常取σε=1.3;Sk、Sε為用戶定義的源項。
2 建立模型
2.1 基本假設
對模擬條件做以下基本假設[6]:1)煤粉在水平管道中輸送時,煤粉與空氣共存并相互滲透,兩相在數值模擬計算域中的任一點共存,但分別具有各自的速度、濃度和體積分數;2)煤粉具有其自身的湍流黏性等湍流輸送性質和類似于連續流體的物理性質;3)管內煤粉和空氣兩相流動充分發展且為定常流動;4)視空氣為牛頓流體。
2.2 模型建立與網格劃分
本章以煤粉在輸送過程中典型的水平管道為研究對象,幾何模型如圖1所示,管道長度為10 m,內徑為105 mm,網格劃分如圖2和圖3所示。網格質量較高,采用六面體結構化網格,共87.5萬個網格。
3 模擬結果與分析
3.1 煤粉濃度對比分析

圖1 幾何模型

圖2 進出口端面

圖3 壁面
圖4為在距管道入口軸向距離6 m處,風速分別為25 m/s、20 m/s、15 m/s和10 m/s時煤粉濃度沿管道徑向的分布云圖。對比4種不同風速下的煤粉濃度分布可知,在煤粉輸送過程中,隨著風速的減小,管道上半部的煤粉濃度不斷減小,大量集中在管道的底部,沉積現象加重,當風速降低至10 m/s時,管道上半部煤粉的含量幾乎為0,大量的煤粉沉積在管道底部,嚴重影響了煤粉輸送效果,同時還增加了輸運管道堵塞的危險,使清理管道的成本上升。
對4種不同風速下煤粉的濃度分布圖進行分析可知,當風速為25 m/s時,煤粉在管道內的分布最為均勻,沉積量最小,輸送效果最好。

圖4 不同速度處的煤粉濃度云圖
圖5為距管道入口軸向距離6 m處,風速分別為25 m/s、20 m/s、15 m/s和10 m/s時,煤粉濃度沿x方向的分布情況,由圖可知,當風速為25 m/s時,煤粉的濃度在0.04到0.16范圍內變化,大量集中在0.1附近;當風速為20 m/s時,煤粉的濃度在0到0.6范圍內變化,煤粉濃度在0.1以下的區域明顯增多;當風速為15 m/s時,煤粉的最高濃度超過0.6,煤粉濃度為0的區域增多,出現嚴重的沉積現象;當風速降到至10 m/s時,煤粉的沉積現象更加嚴重。
通過對不同風速下煤粉濃度分布情況進行分析可知,當風速為25m/s時,煤粉能夠均勻地充滿整個輸送管道,煤粉的輸送效果達到最佳,當風速低于25m/s時,開始出現煤粉的沉積現象,隨著風速的不斷降低,這種現象逐漸嚴重。

圖5 不同速度處的煤粉濃度分布散點圖

圖6 不同速度處的煤粉速度云圖

圖7 不同速度處的煤粉速度分布散點圖
3.2 煤粉速度對比分析
圖6為在距管道入口軸向距離6 m處,風速分別為25 m/s、20 m/s、15 m/s和10 m/s時的煤粉顆粒運動速度徑向分布云圖,從圖中可以看出煤粉顆粒的運動速度分布表現為最高速度集中在管道中上部,當煤風速度為25 m/s時,煤粉顆粒的速度分布相對來說比較均勻,但當速度小于25 m/s時,速度分布不均勻度急劇上升,當風速為10 m/s時,煤粉顆粒的運動速度分布極度不均勻,且其運動速度明顯小于風速。
圖7為距管道入口軸向距離6 m處,風速分別為25 m/s、20 m/s、15 m/s和10 m/s時,煤粉顆粒運動速度沿x方向的分布情況。
由圖7可知,當風速為25 m/s時,煤粉顆粒的運動速度集中在20 m/s到30 m/s的范圍之內,煤粉場與空氣場的耦合效果最佳;隨著風速的不斷降低,煤粉顆粒的運動速的分布范圍逐漸擴大,不均勻度增加,煤粉場與空氣場的耦合效果不斷變差,嚴重影響著煤粉的輸送效果,隨著煤粉的不斷沉積,甚至會造成煤粉輸送管道的嚴重堵塞,增加煤粉輸運的成本。
4 結 論
通過對煤粉輸送過程中,風速對煤粉濃度分布和速度分布影響的模擬和分析,得出以下結論:1)隨著風速的不斷提高,煤粉場與空氣場的耦合效果不斷提高,煤粉的濃度分布和速度分布不斷趨于均勻,煤粉的輸送效率不斷提高;2)當風速提高至25 m/s時,煤粉場和空氣場的耦合效果得到明顯提升,煤粉的濃度分布和速度分布基本均勻,煤粉的輸送效果能夠滿足生產的需要;3)如果將風速進一步提高,很明顯會進一步提高煤粉的輸送效果,但是在煤粉輸送效果提高的同時,由于風速的提高需要,對供風系統要求變高,供風系統的能耗也會隨之增加。
因此,綜合考慮效率、經濟和環保各方面的因素,本文認為煤粉在水平管道內均勻輸送和不發生沉積的煤風速度應不小于25 m/s。
[參考文獻]
[1] 付祥釗.計算流體力學[M].重慶:重慶大學出版社,2007.
[2] 王安麟,孟井泉,楊興,等.基于雙流體模型的簡易化兩相攪拌流場[J].機械設計,2007,24(6):45-48.
[3] 趙立娟.不同粒徑泥沙管道水力輸送阻力特性研究[D].南京:河海大學,2002.
[4] 沈宗沼,楊定軍,劉愛圓,等.液固兩相流泵葉輪內流場數值分析與試驗研究[J].煤炭機械,2010,31(1):26-59.
[5] 劉義倫,劉生奇,劉偉濤.水泥窯用燃燒器三維流場冷態數值模擬[J].機械設計與研究,2012,28(1):113-116.
[6] 裴宇.褐煤煤粉的高壓密相氣力輸送試驗與數值模擬研究[D].南京:東南大學,2015.

