基于節(jié)點有限元與矢量有限元的可控源電磁三維正演對比

湯文武 柳建新 葉益信 張 華(東華理工大學(xué)地球物理與測控技術(shù)學(xué)院，江西南昌 330013； 中南大學(xué)地球科學(xué)與信息物理學(xué)院，湖南長沙 410083)

1 引言

電磁法是根據(jù)電磁感應(yīng)原理研究天然電磁場或人工(可控)場源在大地中激勵的交變電磁場分布， 并由觀測到的電磁場分布研究地下目標(biāo)體的電性及地質(zhì)特征的一種地球物理方法[1]，已被廣泛地應(yīng)用于金屬礦勘探[2，3]、地下水資源調(diào)查[4]、油氣田勘探[5]、油氣動態(tài)監(jiān)測[6]等領(lǐng)域。根據(jù)場源的類型可分為天然源及可控源兩類，現(xiàn)今可控源電磁法發(fā)展迅速，但場源的引入給其資料處理和解釋帶來了諸多困難。作為資料解釋的重要手段，正反演技術(shù)的發(fā)展對進一步推動可控源電磁法的廣泛應(yīng)用具有重要作用，尤其是三維正、反演方法，已成為研究熱點。

針對三維可控源電磁法的正演問題，近年來國內(nèi)外學(xué)者開展了大量研究。Newman等[7]采用基于二次電場的Helmholtz 方程，將全空間或?qū)訝畎肟臻g電磁場響應(yīng)作為一次場引入到方程右端，避免了直接模擬電偶源或磁偶源的困難。利用交錯網(wǎng)格有限差分法對Helmholtz方程進行離散，得到的復(fù)系數(shù)線性方程組通過雅可比預(yù)處理的QMR(quasi-minimal residual method)迭代法進行求解，提高了正演效率。Weiss等[8]利用有限差分法對三維各向異性介質(zhì)的電磁感應(yīng)問題進行了正演模擬，并采用全張量表示電導(dǎo)率參數(shù)，更有利于解決實際問題。Streich[9]利用MUMPS直接求解器對有限差分法離散頻率域可控源電磁方程得到的線性方程組進行求解，對于中等規(guī)模的求解問題精度高，且適用于多激發(fā)源的正演計算。Badea等[10]利用有限單元法計算了三維可控源的電磁響應(yīng)，通過二次耦合勢的引入消除了源的奇異性，并通過局部網(wǎng)格加密提高了求解精度。Stalnaker[11]利用基于非結(jié)構(gòu)化四面體網(wǎng)格的有限元對三維可控源電磁進行正演模擬，采用基于二次耦合勢的方式避免了直接模擬場源。基于非結(jié)構(gòu)化的四面體網(wǎng)格能夠適應(yīng)更復(fù)雜的地形及地質(zhì)體結(jié)構(gòu)，且模擬精度很高。Farquharson等[12]采用矢量有限元進行大地電磁三維正演，并在各個單元接觸面上施加散度校正以提高正演計算速度。Puzyrev等[13]利用節(jié)點型有限單元法求解基于二次耦合勢的三維可控源電磁方程，并考慮了電導(dǎo)率的各向異性。Tong等[14]利用有限單元法對三維大地電磁法進行了正演模擬，通過將散度校正引入到有限元方程中，避免了偽解的出現(xiàn)。徐志峰等[15]基于磁矢量勢及電標(biāo)量勢將Maxwell方程轉(zhuǎn)化為位勢的類Helmholtz方程，通過引入罰項及穩(wěn)定化方法避免了偽解及數(shù)值不穩(wěn)定，采用有限元方法計算了三維可控源的電磁響應(yīng)。另外，付長民等[16]、殷長春等[17]、王超[18]、韓波等[19]、湯文武等[20]、嚴(yán)波等[21]、李建慧等[22]分別對三維可控源電磁正演問題開展了研究。

有限單元法由于其對地形及不規(guī)則異常體具有很好的適應(yīng)性受到廣泛關(guān)注[23]。對于有限單元法在三維可控源電磁中的應(yīng)用，早期主要采用節(jié)點型有限元，其概念及實現(xiàn)相對簡單，但可能存在偽解問題。近年來，矢量有限元法逐步獲得更多關(guān)注，究其原因在于矢量有限元在電導(dǎo)率分界面上自動滿足電磁場的邊界條件，可消除偽解。但目前并未見兩種正演方法實際應(yīng)用的詳細(xì)對比。因此，基于前人研究成果，本文開展關(guān)于節(jié)點有限元及矢量有限元在三維頻率域可控源電磁正演計算的應(yīng)用對比，旨在為兩種方法的合理選用提供參考。

2 理論基礎(chǔ)

頻率域可控源電磁法的三維正演可基于電場開展，亦可依據(jù)耦合勢進行，文中的三維正演是基于二次電場的有限元正演，可避免源的奇異性，與總場正演方式相比，同等條件下具有可采用更小網(wǎng)格的優(yōu)勢。基于節(jié)點有限元與矢量有限元的三維正演，其基本方程是一致的，但具體處理邊值問題時會有所差異。文中矢量有限元三維正演實現(xiàn)是基于筆者已發(fā)表的成果[20]，為了敘述完整，以下簡要討論其基本原理。

2.1 基于二次電場的偏微分方程

電磁場理論是可控源電磁法的基本理論。頻率域中，在準(zhǔn)靜態(tài)條件下(忽略位移電流)，電磁場滿足以下麥克斯韋方程組

(1)

(2)

式中：E為電場矢量(單位為V/m)；H為磁場矢量(單位為A/m)；Jc為外電流密度矢量(單位為A/m2)；μ0為真空中的磁導(dǎo)率；σ為地下電性介質(zhì)的電導(dǎo)率。在式(1)和式(2)中，時諧因子設(shè)為e-iω t。聯(lián)立方程式(1)和式(2)，可得到以下關(guān)于電場矢量的雙旋度方程

(3)

為了消除場源引起的奇異性，常將總場分解為一次場和二次場。通過預(yù)先選定某個簡單參考模型，利用計算得到的一次場Ep求解二次場Es，并最終得到總場，即

E=Ep+Es

(4)

對于一次場Ep，同樣可得以下雙旋度方程

(5)

式中σp為預(yù)先選定的參考模型的電導(dǎo)率分布，一般可選為全空間、均勻半空間或水平層狀介質(zhì)模型以簡化一次場的計算。用式(3)減去式(5)，并化簡，得到

(6)

式中σa為異常電導(dǎo)率分布，且有σa=σ-σp。

2.2 邊界條件

采用一次場、二次場分離的方式計算總場時，邊界條件可以取得比較簡單。當(dāng)邊界距離目標(biāo)研究區(qū)域足夠遠(yuǎn)時，二次場可近似為零。因此，采用如下狄利克雷邊界條件

n×Es=0

(7)

式(6)、式(7)便構(gòu)成了可控源電磁三維正演的邊值問題。這里，選定均勻半空間模型計算一次場，其水平電偶極的諧波場存在解析積分公式[24]，具體表達式見附錄A。積分表達式中都是含有第一類貝塞爾函數(shù)J0或J1項的漢克爾變換，可利用數(shù)字線性濾波器快速求解，本文采用的是Guptasarma等[25]提出的數(shù)值濾波算法。

3 有限元分析

對于上節(jié)建立的邊值問題，可采用節(jié)點有限元或矢量有限元方法求解。為簡單起見，這里僅以長方體剖分單元為例展開討論。當(dāng)采用節(jié)點有限元時，電磁場分量置于節(jié)點上采樣，而矢量有限元則將電磁場分量置于各個單元的棱邊上采樣(圖1)。圖1a為節(jié)點有限元中各個電場分量的分布，每個節(jié)點上都布置有電場三分量，因此每個單元有24個自由度；而圖2b為矢量有限元各個電場分量的布置，每條棱邊上都有與之平行的電場分量，每個單元的自由度為12。

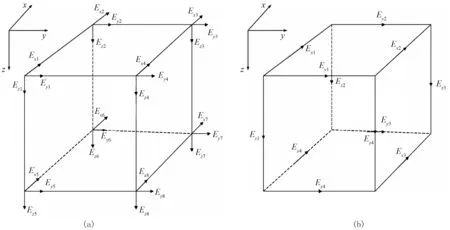
圖1 電場分量在節(jié)點有限元(a)和矢量有限元(b)的剖分單元中的布置示意圖

對于以上邊值問題，基于變分原理可推導(dǎo)相應(yīng)的變分問題如下

iωμ0σaEs·Ep]dV

(8)

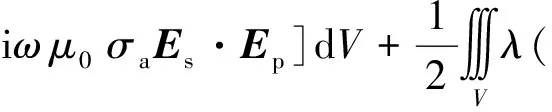
(9)

式中λ是調(diào)節(jié)散度項在以上泛函表達式的比重因子，當(dāng)取值為1時可獲得較滿意結(jié)果。

當(dāng)采用矢量有限元時，由于矢量元在棱邊上取樣，在各個單元內(nèi)自動滿足散度條件，因此不需要在各個剖分單元內(nèi)施加散度條件。但進一步研究發(fā)現(xiàn)，基于矢量有限元求解時獲得的有限元方程的剛度矩陣條件數(shù)很大，采用迭代法收斂很慢，原因是在不同單元接觸面上可能不滿足散度條件，因此有必要進一步校正以加速迭代法求解過程。

4 模型實例對比

為了對比節(jié)點有限元與矢量有限元在三維可控源電磁中的模擬效果，設(shè)計了兩個模型開展正演計算，包括一個存在解析解的水平層狀介質(zhì)模型及一個無解析解的低阻體模型。所有模擬結(jié)果都是設(shè)定兩種方法在同一剖分網(wǎng)格及線性方程組求解器的情況下獲得的。采用的計算平臺(laptop)為：Windows 7；CPU，Intel i7-3610qm；8GB RAM。

4.1 水平層狀介質(zhì)模型

水平層狀介質(zhì)模型的電磁響應(yīng)具有解析表達式，這里選用如圖2所示的三層水平介質(zhì)模型對正演計算結(jié)果進行對比驗證。場源取為單位電偶源并置于原點處，分別計算1～8192Hz按對數(shù)等間隔分布的14個頻率的電磁響應(yīng)。采用的網(wǎng)格為91×76×50，其中z方向包含20個空氣層單元和30個地下介質(zhì)層單元。圖3展示了坐標(biāo)為(0，-2300m，0)的測深點處卡尼亞視電阻率及相位的解析解、節(jié)點有限元及矢量有限元卡尼亞視電阻率及相位的數(shù)值解，其中圖3a為卡尼亞視電阻率曲線的對比，圖3b為相位曲線的對比。

圖2 水平三層介質(zhì)模型

由圖3a定性分析可知：矢量有限元獲得的卡尼亞視電阻率曲線與解析解吻合很好，而節(jié)點有限元獲得的卡尼亞視電阻率數(shù)值大體上與解析解吻合，但在個別低頻及高頻端數(shù)據(jù)誤差較大。進一步由計算結(jié)果統(tǒng)計可知，對于卡尼亞視電阻率而言，矢量有限元數(shù)值解所有頻點數(shù)據(jù)誤差在1%以下，平均誤差為0.17%；節(jié)點有限元數(shù)值解高頻、低頻段數(shù)據(jù)誤差大，中間頻段數(shù)據(jù)誤差小，基本在3%以下。對圖3b做類似分析可知，矢量有限元數(shù)值解整體上與解析解吻合較好，平均誤差為4.4%；而節(jié)點有限元在低頻、高頻段誤差大，中間頻段數(shù)據(jù)誤差小，基本在5%以下。

進一步通過模擬實驗可知，縮小中間網(wǎng)格剖分間距可以改善節(jié)點有限元在高頻段誤差大的現(xiàn)象，因此高頻段的誤差大主要跟網(wǎng)格剖分有關(guān)，相比矢量有限元而言需要更密的網(wǎng)格才能達到合理的精度。但低頻段的誤差通過網(wǎng)格剖分控制基本無法進一步改善，可能的原因應(yīng)該是與節(jié)點有限元方法本身有關(guān)。

由于本文算法是基于二次場開展的，因此，為了更準(zhǔn)確地對比矢量有限元與節(jié)點有限元的計算精度，有必要直接針對二次場進行對比。圖4所示是坐標(biāo)為(0，-2300m，0)的測深點處的二次電場Exs的對比圖，其中二次場的解析解由圖2中三層介質(zhì)模型及另一個電阻率為100Ω·m的均勻半空間模型的解析解之差獲得。圖4a代表二次電場分量Exs實部絕對值(以|Re(Exs)|表示)的對比，圖4b代表二次電場分量Exs虛部絕對值(以|Im(Exs)|表示)的對比。由圖可知，矢量有限元及節(jié)點有限元求解獲得的二次場與解析解基本吻合，但相比而言，矢量有限元精度更高。

圖3 卡尼亞視電阻率(a)及相位曲線(b)對比圖

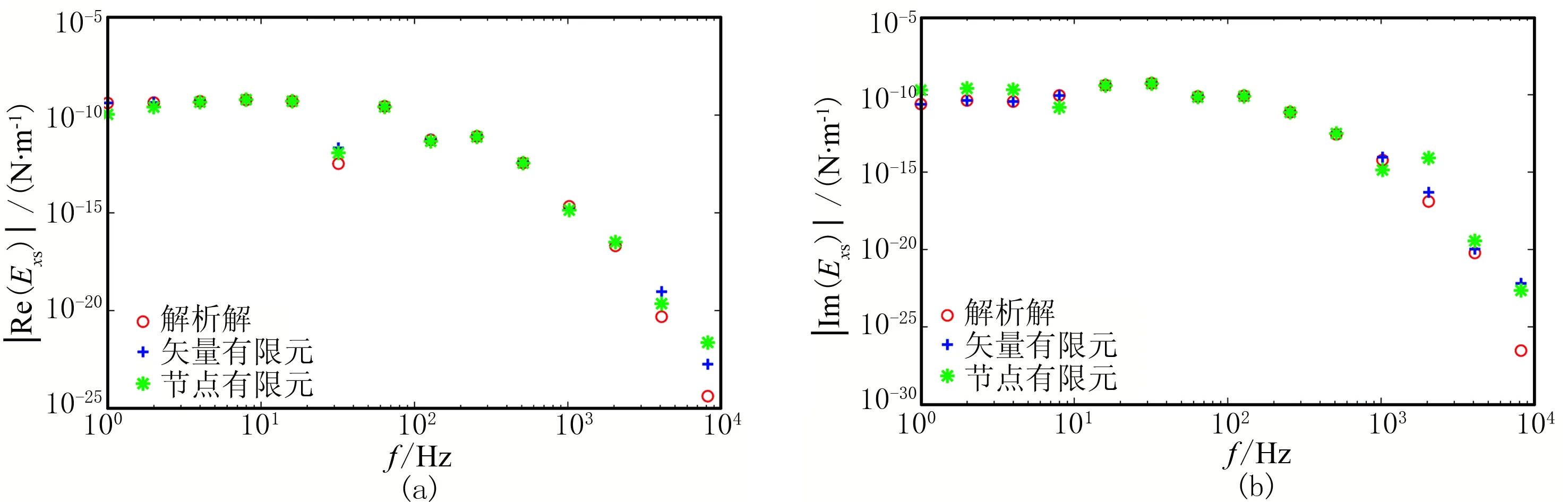
圖4 二次電場實部分量(a)和虛部分量(b)曲線對比圖

4.2 單一低阻體模型

以一個單一低阻體模型為實例，分別進行基于節(jié)點有限元及矢量有限元法的三維可控源電磁響應(yīng)模擬，并作對比。圖5是其斷面(圖5a)及平面(圖5b)示意圖。該模型描述了一個置于電阻率為100Ω·m的均勻半空間的長方體低阻體，激發(fā)源為單位電偶源，距離低阻體的最大水平距離為8.8km。該低阻體長、寬、高分別為0.6、0.5、0.2km，電阻率為10Ω·m。

統(tǒng)一采用91×116×50的網(wǎng)格對該模型進行正演計算，圖6分別給出了采用節(jié)點有限元及矢量有限元法的模擬結(jié)果。圖6a為節(jié)點有限元視電阻率不同頻率下的三維等值線切片圖； 圖6b為矢量有限元法正演結(jié)果對應(yīng)的切片。5個不同切片分別對應(yīng)64、32、16、8、4Hz。由頻率測深原理可知，5個不同切片分別對應(yīng)由淺至深的地下介質(zhì)的電阻率分布及變化情況。由于采用相同色標(biāo)，因此顏色的變化即體現(xiàn)了視電阻率的變化。從圖中等值線分布情況來看，兩種正演方法得到的不同頻率下的視電阻率分布形態(tài)基本一致，因此相互驗證了各自正演算法的正確性。

具體分析各張切片圖：64Hz切片，盡管從等值線分布看兩種方法差別較大，但實際上視電阻率基本等于均勻大地的電阻率(100Ω·m)，此時趨膚深度最小，低阻體的影響基本可忽略； 從32Hz逐步過渡到8Hz，隨著趨膚深度增大，低阻體影響顯現(xiàn)出來，切片圖上可見藍(lán)色低值區(qū)，視電阻率最低約為86Ω·m； 4Hz對應(yīng)的切片未見明顯低值區(qū)，視電阻率普遍高于100Ω·m，此時已基本進入近區(qū)。因此，分析不同頻率下切片圖的變化也在一定程度上驗證了正演算法的正確性。

對于高維電磁正演計算，有限元分析得到的往往是一個大型、稀疏、對稱復(fù)系數(shù)線性方程組，其求解是正演計算重點考慮的一個問題。采用預(yù)處理的QMR迭代法求解線性方程組時，統(tǒng)計了兩種不同算法在不同頻率的迭代殘差。如圖7所示，圖7a為節(jié)點有限元方程在不同頻率下的正演收斂曲線，圖7b為矢量有限元方程在不同頻率下的正演收斂曲線。

圖5 低阻體模型斷面(a)和平面(b)示意圖

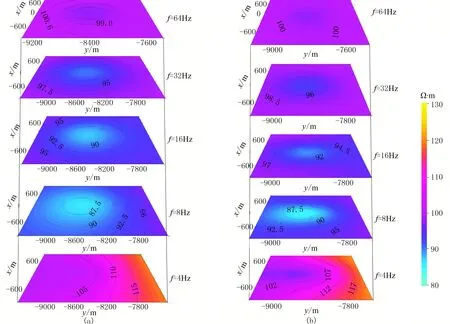
圖6 節(jié)點有限元法(a)和矢量有限元法(b)模擬的不同頻率下視電阻率三維等值線切片圖

圖7 不同頻率下的迭代收斂曲線圖(a)節(jié)點有限元法； (b)矢量有限元法

分析圖7a可知，不同頻率的迭代收斂曲線基本一致，大約80次迭代可使得相對誤差降到10-6；分析圖7b可知，不同頻率下線性方程組求解的收斂曲線區(qū)別較大，總體規(guī)律是：頻率越低，迭代收斂越慢，達到同等精度需要更多迭代次數(shù)。因此，當(dāng)采用迭代法求解有限元方程時，矢量有限元正演計算速度受頻率影響較大，且迭代收斂較節(jié)點有限元明顯要慢。表1給出了兩種正演計算在各個頻點的計算時間，總體而言，節(jié)點有限元在不同頻率下計算時間基本一致，而矢量有限元低頻時正演計算時間長。值得注意的是，盡管從自由度的角度來分析，矢量有限元的自由度小于節(jié)點有限元的自由度，同等條件下節(jié)點有限元離散得到的剛度矩陣更大。但由于節(jié)點有限元線性方程組迭代求解收斂較矢量有限元快，矢量有限元總體正演時間較節(jié)點有限元長，平均到各個頻率基本上矢量有限元計算速度較節(jié)點有限元慢一半。

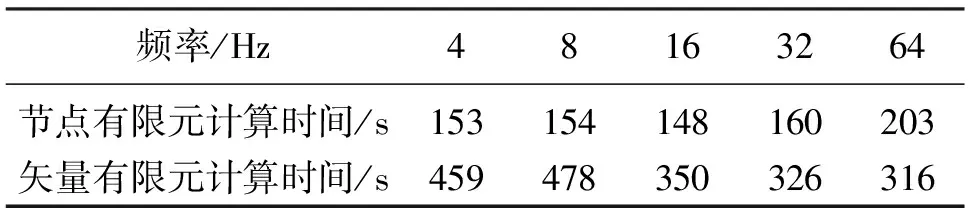
表1 各頻率下正演計算時間對比

5 結(jié)論

本文對節(jié)點有限元和矢量有限元可控源電磁三維正演問題進行對比、分析，在控制并確保網(wǎng)格剖分一致并采用相同線性方程組求解器的情況下，得出以下認(rèn)識和結(jié)論：

(1)同等情況下，矢量有限元求解精度較節(jié)點有限元精度高，在全頻率都能取得滿意的計算結(jié)果；而節(jié)點有限元在低頻段正演計算精度不高；

(2)采用迭代法求解有限元方程時，矢量有限元正演計算速度跟頻率有較大關(guān)系，通常來說，頻率越低，正演速度越慢；而強加散度條件的節(jié)點有限元正演計算速度與頻率關(guān)系不大；

(3)同等情況下，節(jié)點有限元正演計算速度較矢量有限元法快1倍以上。

總之，在計算效率優(yōu)先的情況下可考慮選擇節(jié)點有限元開展正演計算；當(dāng)計算精度是第一指標(biāo)時應(yīng)當(dāng)選用矢量有限元開展正演計算。

附錄A 水平電偶極源的諧波場

在水平電偶極源激發(fā)下，均勻半空間模型在地面上的電磁場響應(yīng)可利用已有的積分公式計算，但由于基于二次場的三維正演模擬要利用地下空間的一次場，因此還需另外推導(dǎo)相應(yīng)的積分公式。

考夫曼等[24]通過頻率域和時間域電磁測深法推導(dǎo)了均勻半空間模型上水平電偶極源在地面上的電磁場響應(yīng)。基于此，本文進一步推導(dǎo)了地下空間的電磁場響應(yīng)的積分表達式。

圖A-1為一個均勻半空間模型，x軸沿正北方向，y軸沿正東方向，z軸豎直向下。時諧電流為I，長為dl的水平電偶極子位于坐標(biāo)原點。均勻半空間的電導(dǎo)率為σb，設(shè)電磁場待求點為P，P與原點的距離為r，r與x軸的夾角為φ。假設(shè)時諧因子為e-iω t。均勻半空間電磁場矢量可由一個矢勢及一個標(biāo)勢來表示(不考慮位移電流作用)

(A-1)

(A-2)

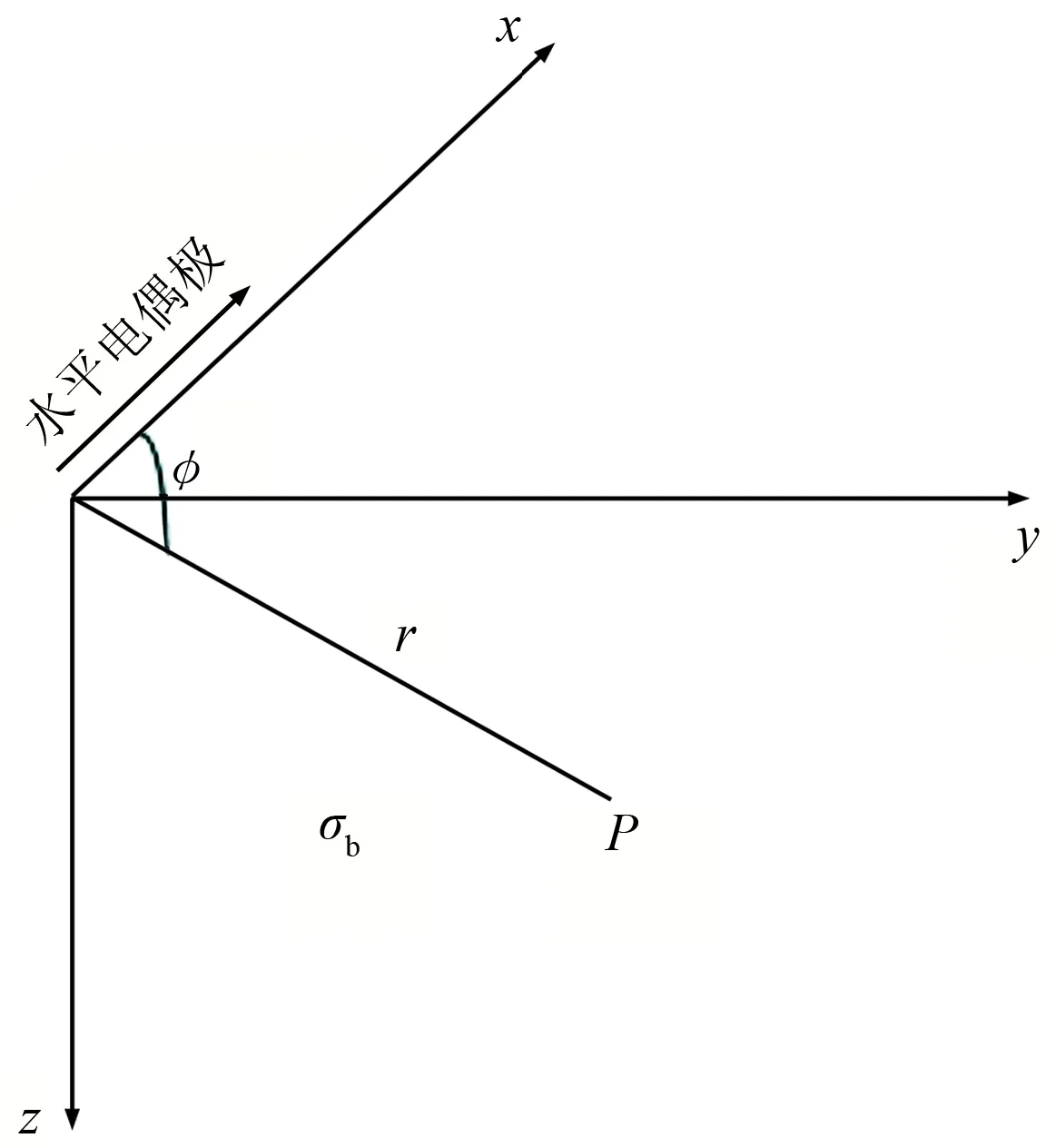
圖A-1 水平電偶極激發(fā)下的均勻半空間模型

(A-3)

(A-4)

且電場矢量可用矢勢單獨表示

(A-5)

依據(jù)文獻[24]的推導(dǎo)，假設(shè)Ay=0并求解式(A-4)，可得地下空間中矢勢的其他二分量積分表達式

(A-6)

(A-7)

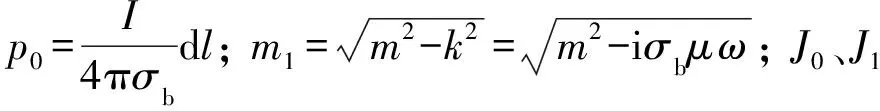
(A-8)

采用圓柱坐標(biāo)系，將式(A-6)～式(A-8)代入式(A-5)并整理，可得電場三分量表達式

(A-9)

(A-10)

(A-11)

同理，結(jié)合式(A-1)、式(A-6)和式(A-7)亦可得到磁場三分量表達式。

參考文獻

[1] 湯井田，何繼善．可控源音頻大地電磁法及其應(yīng)用．湖南長沙：中南大學(xué)出版社，2005.

Tang Jingtian，He Jishan．The Controlled-Source Audio-frequency Magnetotellurics and Its Application．Central South University Press，Changsha，Hunan，2005.

[2] Nabighian M，Corbett J．Electromagnetic Methods in Applied Geophysics：Theory．SEG，1988.

[3] 楊懷杰，潘和平，孟慶鑫等．導(dǎo)電圍巖對井中三維瞬變電磁響應(yīng)的影響規(guī)律研究．石油物探，2016，55(2)：288-293.

Yang Huaijie，Pan Heping，Meng Qingxin et al．Influence laws of conductive host on borehole 3D transient electromagnetic responses．GPP，2016，55(2)：288-293.

[4] 柳建新，麻昌英，孫麗影等．可控源音頻大地電磁測深法在地?zé)峥碧街械膽?yīng)用．工程地球物理學(xué)報，2014，11(3)：319-325.

Liu Jianxin，Ma Changying，Sun Liying et al．The application of CSAMT to the geothermal exploration．Chinese Journal of Engineering Geophysics，2014，11(3)：319-325.

[5] He Z，Liu X，Qiu W et al．Mapping reservoir boundary by borehole-surface TFEM：Two case studies．The Leading Edge，2005，24(9)：896-900.

[6] Wirianto M，Mulder W A，Slob E C．A feasibility study of land CSEM reservoir monitoring in a complex 3-D model．Geophysical Journal of the Royal Astronomical Society，2010，181(2)：741-755.

[7] Newman G A，Alumbaugh D L．Frequency-domain modelling of airborne electromagnetic responses using staggered finite differences．Geophysical Prospecting，1995，43(8)：1021-1042.

[8] Weiss C，Newman G．Electromagnetic induction in a generalized 3D anisotropic earth，Part 2：The LIN preconditioner．Geophysics，2003，68(3)：922-930.

[9] Streich R．3D finite-difference frequency-domain mode-ling of controlled-source electromagnetic data：Direct solution and optimization for high accuracy．Geophy-sics，2009，74(5)：F95-F105.

[10] Badea E A，Everett M E，Newman G A et al．Finite-element analysis of controlled-source electromagnetic induction using Coulomb-gauged potentials．Geophy-sics，2001，66(3)：786-799.

[11] Stalnaker J L．A Finite Element Approach to the 3D CSEM Modeling Problem and Applications to the Study of the Effect of Target Interaction and Topo-graphy [D]．Texas A & M University，2004.

[12] Farquharson C G，Miensopust M P．Three-dimensional finite-element modelling of magnetotelluric data with a divergence correction．Journal of Applied Geophysics，2011，75(4)：699-710.

[13] Puzyrev V，Koldan J，Puente Jdl et al．A parallel finite-element method for three-dimensional controlled-source electromagnetic forward modelling．Geophysical Journal International，2013，193(2)：678-693.

[14] Tong X Z，Liu J X，Xie W et al．Three-dimensional forward modeling for magnetotelluric sounding by finite element method．Journal of Central South University of Technology，2009，16(1)：136-142.

[15] 徐志鋒，吳小平．可控源電磁三維頻率域有限元模擬．地球物理學(xué)報，2010，53(8)：1931-1939.

Xu Zhifeng，Wu Xiaoping．Controlled source electromagnetic 3-D modeling in frequency domain for finite element method．Chinese Journal of Geophysics，2010，53(8)：1931-1939.

[16] 付長民，底青云，王妙月．海洋可控源電磁法三維數(shù)值模擬．石油地球物理勘探，2009，44(3)：358-363.

Fu Changmin，Di Qingyun，Wang Miaoyue．The 3D numerical modeling for MCSEM．OGP，2009，44(3)：358-363.

[17] 殷長春，賁放，劉云鶴等．三維任意各向異性介質(zhì)中海洋可控源電磁法正演研究．地球物理學(xué)報，2014，57(12)：4110-4122.

Yin Changchun，Ben Fang，Liu Yunhe et al．MCSEM 3D modeling for arbitrarily anisotropic media．Chinese Journal of Geophysics，2014，57(12)：4110-4122.

[18] 王超．海洋可控源電磁法三維正演研究[學(xué)位論文]．北京：中國地質(zhì)大學(xué)(北京)，2014.

Wang Chao．Marine CSEM 3D Forward Modeling [D]．China University of Geosciences (Beijing)，Beijing，2014.

[19] 韓波，胡祥云，Schultz A等．復(fù)雜場源形態(tài)的海洋可控源電磁三維正演．地球物理學(xué)報，2015，58(3)：1059-1071.

Han bo，Hu Xiangyun，Schultz A et al．Three dimensional forward modeling of marine controlled source electromagnetic field of complex source geometries．Chinese Journal of Geophysics，2015，58(3)：1059-1071.

[20] 湯文武，李耀國，柳建新等．基于二次電場的可控源電磁法三維矢量有限元正演模擬．石油物探，2015，54(6)：665-673.

Tang Wenwu，Li Yaoguo，Liu Jianxin et al．Three-dimensional controlled-source electromagnetic forward modeling by edge-based finite element using secondary electrical field．GPP，2015，54(6)：665-673.

[21] 嚴(yán)波，李予國，韓波等．任意方位電偶源的MCSEM電磁場三維正演．石油地球物理勘探，2017，52(4)：859-868.

Yanbo，Li Yuguo，Hanbo et al．The 3D forward mode-ling of the EM field for MCSEM using the electrical dipole source with arbitrary azimuth．OGP，2017，52(4)：859-868.

[22] 李建慧，胡祥云，陳斌等．復(fù)雜形態(tài)回線源激發(fā)電磁場的矢量有限元解．石油地球物理勘探，2017，52(6)：1324-1332.

Li Jianhui，Hu Xiangyun，Chen Bin et al．The vector finite element solution for the EM field induced by the loop source with complex form．OGP，2017，52(6)：1324-1332.

[23] 趙慧，劉穎，李予國．自適應(yīng)有限元海洋大地電磁場二維正演模擬．石油地球物理勘探，2014，49(3)：578-585.

Zhao Hui，Liu Ying，Li Yuguo．The adaptive finite ele-ment forward modeling for 2D marine MT．OGP，2014，49(3)：578-585.

[24] 考夫曼 A A，凱勒 G V．頻率域和時間域電磁測深．北京：地質(zhì)出版社，1987.

Kaufman A A，Keller G V．Frequency and Transient Sounding．Geological Publishing House，Beijing，1987.

[25] Guptasarma D，Singh B．New digital linear filters for Hankel J0and J1transforms．Geophysical Prospecting，1997，45(5)：745-762.