基于Rife算法的跳頻信號瞬時頻率估計算法研究?

孫微濤 張志寶 羅文峰 汪 帆

（中國人民解放軍63788部隊 渭南 714000）

1 引言

頻率是信號的一個重要參量，在信息對抗中，測定截獲信號的頻率是基本任務之一，因此快速、高精度是頻率估計的基本要求［1］。國內外許多學者對正弦信號頻率估計問題做了研究。Abatzoglou［2］提出利用最大似然估計（Maximum Likelihood，ML）算法或ML改進算法估計正弦信號頻率，估計誤差逼近克拉美羅下限（Cramer-Rao Low Bound，CRLB），因此是最優(yōu)估計，但這些算法復雜度高、計算量大，難以實現(xiàn)實時處理，限制了其進一步應用［3］。

直接采用DFT譜估計法進行正弦波信號頻率估計，計算量小（借助FFT），因而在工程上得到了廣泛應用。但DFT中存在能量泄露和柵欄效應，使得這種方法具有很大的誤差，并且算法精度在很大程度上依賴于采樣長度N。多位學者對正弦波信號頻率估計問題作了進一步研究，相繼提出了多種頻率估計算法。例如Rife算法［4］、Quinn算法［5］、能量重心矯正法［6］、牛頓迭代法［7］、頻率校正復比值法［8］、加三角窗的頻譜校正算法［9］和三次插值頻率估計算法及其改進算法［10］等一系列算法，其中Rife算法因為算法簡單且易于實現(xiàn)而被廣泛應用于信號處理領域。文獻［11］對Rife算法進行了分析，指出Rife算法在被估計信號頻率位于量化頻率點附近且信噪比較低時，算法的頻率估計誤差比較大。為此，本文利用頻譜細化的方法，提出一種改進的Rife頻率估計算法。另外，為了消除Rife算法在信噪比較低時因為插值方向錯誤而增加的頻率估計誤差，本文提出對被估計信號進行加窗處理（非矩形窗）的方法對算法進行進一步的修正。理論分析和仿真實驗證明了算法的可行性和有效性。

2 Rife算法

單一頻率實正弦信號表示為

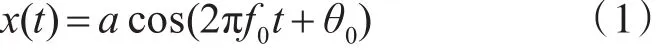
式中：a、f0和θ0分別為正弦信號的幅度、頻率和初相。按等間隔Δt=T/N對x(t)在[ ]0，T 區(qū)間內進行采樣，得到長度為N的序列x(n)，x(n)的N點DFT記為 X(k)，鑒于實序列的DFT對稱性，只考慮離散頻譜的正頻率成份，有

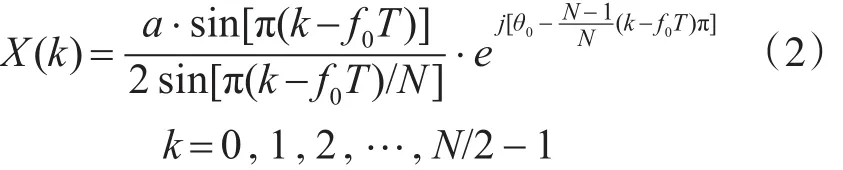
取其中的最大譜線值記作X(k0)。Rife算法主要是利用DFT譜中最大譜線與次大譜線的比值求解相對頻率偏差δ（-0.5～0.5），對FFT算法進行修正，其計算公式為

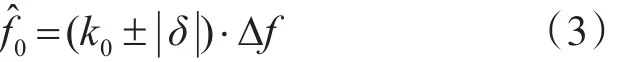
式中：Δf=1/T，為Rife算法的頻率分辨率；正負號根據次大譜線的位置確定。

3 Rife算法的進一步分析

3.1 Rife算法的不足

對Rife算法原理的分析可得Rife算法的頻率估計計算公式為

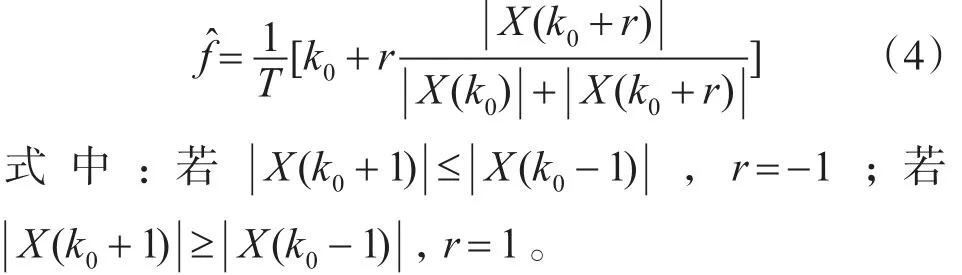
在合適的信噪比條件下，如果信號的實際頻率f處于其DFT譜中最大譜線與次大譜線之間的中心區(qū)域時，Rife算法的估計性能比較好，頻率估計的誤差遠小于直接使用DFT算法。反之，如果信噪比較低且信號頻率 f十分接近其DFT譜中最大譜線的位置時，頻率估計誤差有可能大于直接使用DFT算法。Rife算法的這一特性可以總結為：當信號頻率 f很接近最大譜線與次大譜線中點時，次大譜線的幅度|與最大譜線 | X(k0)|的幅度很接近，此時Rife算法具有較高的估計精度，如圖1所示。

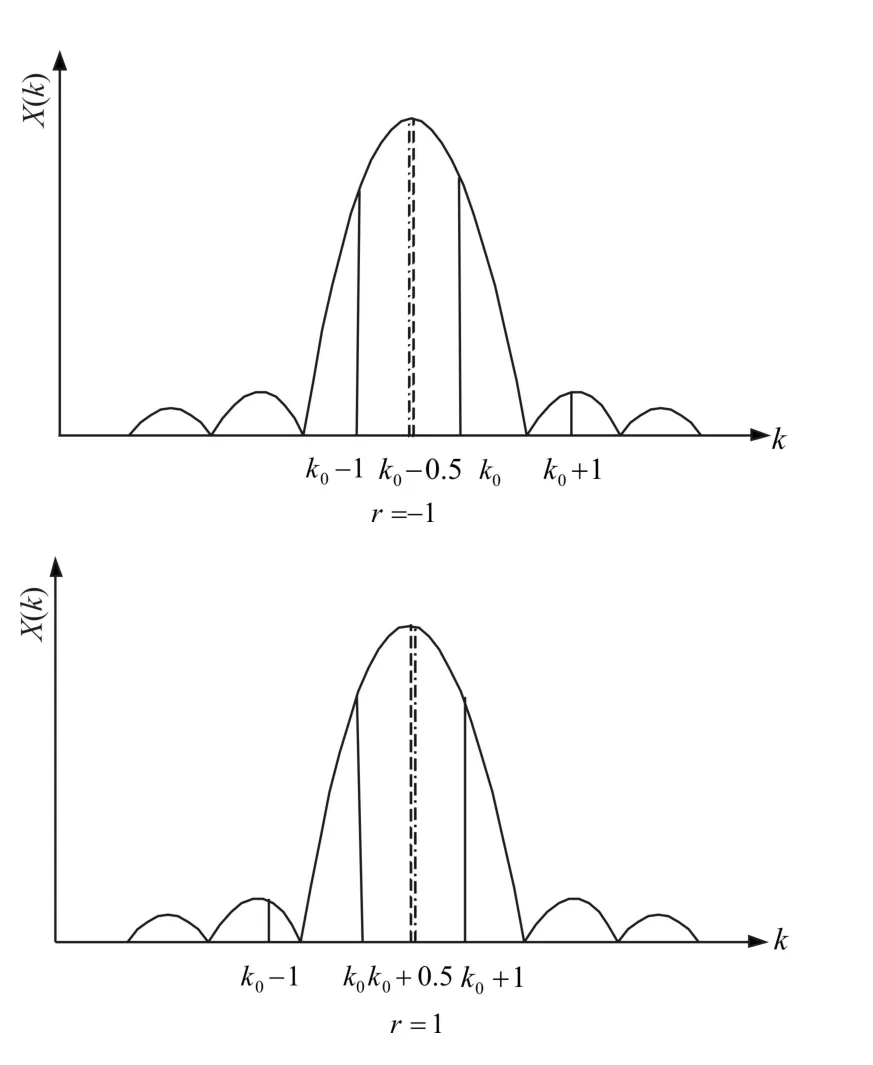
圖1 信號頻率位于最大譜線與次大譜線的中心區(qū)域

當信號頻率 f很接近最大譜線時，即次大譜線的幅度 | X(k0+r)|很小，此時Rife算法的估計精度比較低，如圖2所示。

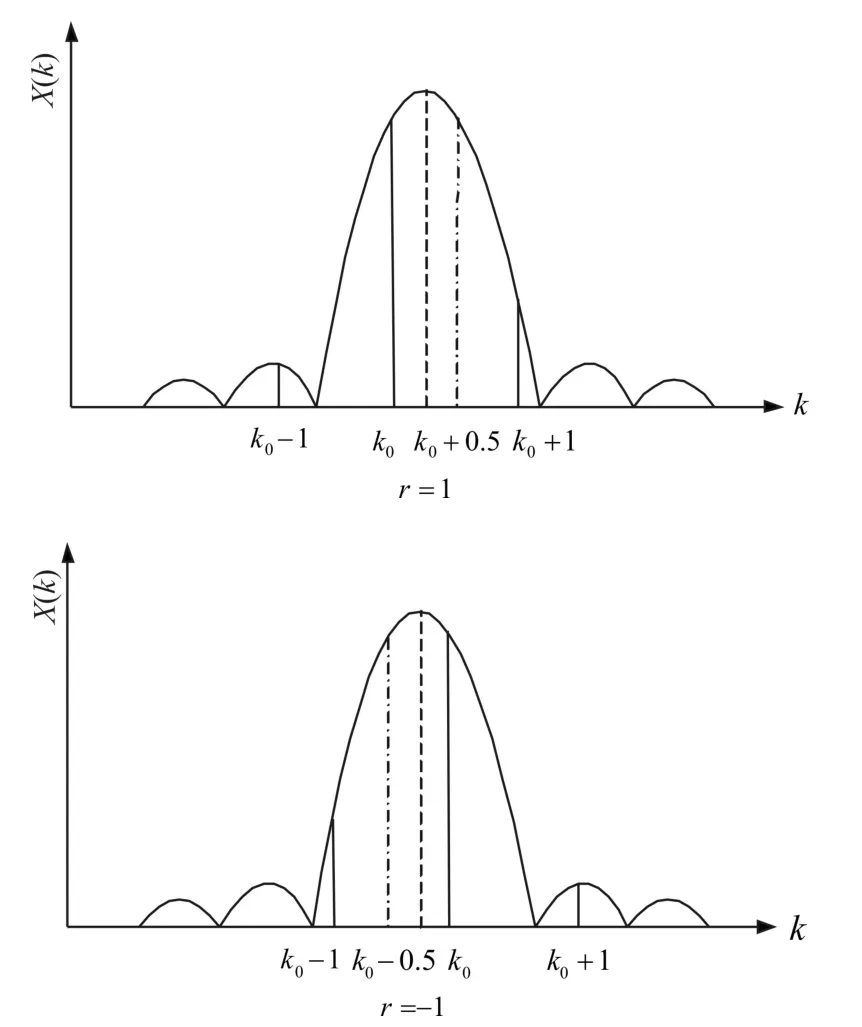
圖2 信號頻率遠離最大譜線與次大譜線的中心區(qū)域

3.2 白噪聲對Rife算法的影響

由圖2和圖3可知，采樣信號DFT譜中的最大譜線和次大譜線都在sinc函數的主瓣內。在沒有噪聲干擾時，信號DFT譜中的次大譜線的幅度永遠大于第一旁瓣內的譜線幅度，因此不會出現(xiàn)插值方向錯誤的情況。但是當有噪聲干擾時，當相對頻率偏差δ的絕對值較小時，有可能出第一旁瓣內的譜線幅度大于主瓣內次大譜線幅度的情況，從而造成頻率插值方向相反，產生較大的頻率估計誤差。

文獻［11］給出了Rife算法頻率估計的總誤差

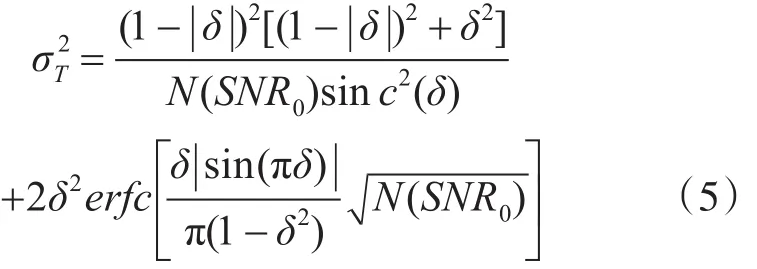
式中erfc()為補誤差函數。Rife算法的頻率估計均方根誤差為

4 改進Rife算法

從第2節(jié)的分析可知，當信號頻率 f位于其DFT譜中兩根最大譜線之間的中心區(qū)域時，Rife算法的估計性能很高；但當信號頻率 f靠近其DFT譜中最大譜線時，算法估計性能急劇下降。針對Rife算法的這一特性，本文提出利用頻譜細化的方法對信號次大譜線的位置進行搬移，從而使信號頻率 f始終位于其DFT譜中兩根最大譜線之間的中心區(qū)域。該算法的基本思想是：定義(k0+1/3，k0+2/3)為離散頻率點k0和k0+1之間的中心區(qū)域，設由Rife算法得到的頻率估計值為 f?，判斷 f?是否位于DFT譜中最大譜線和次大譜線之間的中心區(qū)域，如果是，則將 f?作為最后的頻率估計值，否則對信號DFT譜進行適當的細化，使信號的估計頻率 f?始終位于其DFT譜中兩根最大譜線的中心區(qū)域，這樣就可以保證Rife算法一直具有較高的估計精度。

假設信號采樣序列x(n)經FFT運算法以后的頻譜 X(k)為

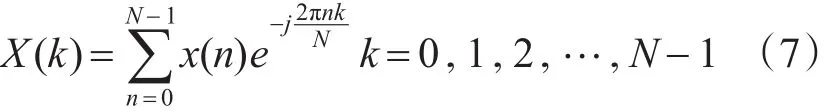
求得最大譜線的位置k0和信號頻率的粗略估計 k0Δf，根據式（3）計算信號頻率估計值 f?。因為始 終 有滿 足≤2/3?Δf，則認為信號頻率估計值 f?位于其DFT譜中最大譜線與次大譜線之間的中心區(qū)域，此時 f?可作為信號頻率的最終估計值。反之，則需要進行修正。

由FFT變換后的幅度譜曲線可知，利用頻譜細化的方法可以求出X(k0±0.5)。假設次大譜線位于最大譜線的左側，則利用 X(k0-0.5)和X(k0)估計信號的實際頻率。若X(k0)≥X(k0-0.5)，則

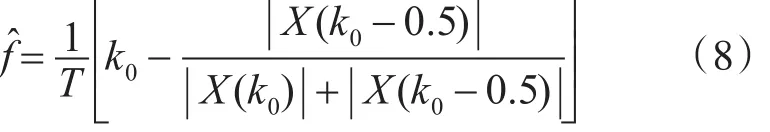
若 X(k0)＜X(k0-0.5)，則

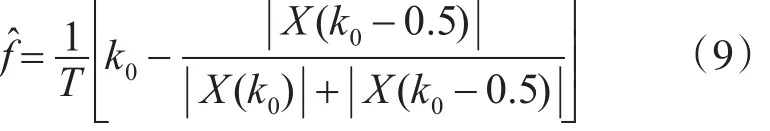
由式（8）或式（9）求得信號頻率的估計值 f?，如果滿足1/3頻率估計的最終值，否則還需要對 X(k0-0.5)和X(k0)之間的信號在進行細化，直至求得的信號頻率的估計值

為了消除Rife算法由于插值方向錯誤而增大的頻率估計誤差，本文提出在對信號進行DFT變換之前對信號進行加窗（非矩形窗）處理。對信號進行加窗處理之后可以使信號DFT譜的主瓣寬度變寬，從而使主瓣內可以包含更多譜線，同時也使得位于最大譜線兩側的次大譜線和第三大譜線更容易區(qū)分，從而避免出現(xiàn)插值方向錯誤的情況。

改進Rife算法的算法流程圖如圖3所示。

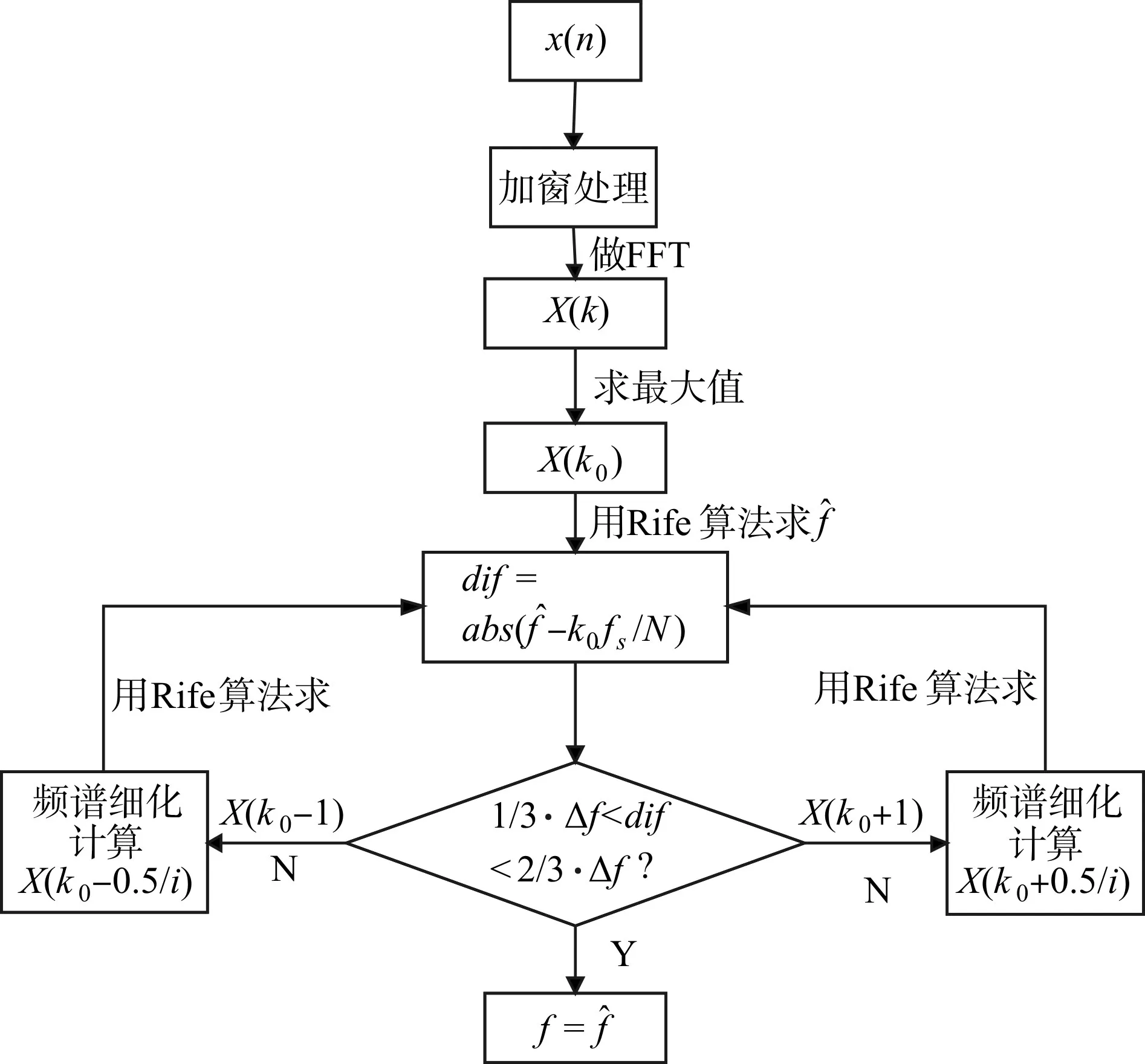
圖3 改進Rife算法流程圖

具體的算法步驟如下。

1）對采樣信號x(n)進行加窗處理并做FFT運算，得 X(k)；

2）對 X(k)進行模運算，并求其最大值X(k0)；

3）利用Rife算法求得信號頻率的估計值 f?；

4）計算信號頻率估計值 f?與信號頻率粗略估計值 k0fs/N差值的絕對值 dif。若1/3?Δf＜dif≤2/3?Δf ，轉向步驟6），否則繼續(xù)步驟5）；

5）當次大譜線位于最大譜線的左側時，進行一次頻譜細化得 X(k0-0.5/i)，其中i為頻譜細化的次數（i=1，2，……）。再次利用Rife算法對信號進行頻率估計，求得信號頻率的估計值 f?。當次大譜線位于最大譜線的右側時，進行一次頻譜細化得 X(k0+0.5/i)，其中i為頻譜細化的次數（i=1，2，……）。再次利用Rife算法對信號進行頻率估計，求得信號頻率的估計值 f?，轉向步驟4）；

6）此時由改進Rife算法得到的信號頻率估計值 f?即為信號最終的估計頻率。

5 仿真及結果分析

設仿真信號為

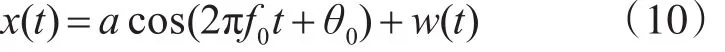
式中：w(t)是均值為0、方差為σ2的高斯白噪聲。信號的信噪比定義為 SNR=a2/σ2。采樣頻率fs=200kHz，采樣間隔 Δt=5×10-6s，樣本點數N=1024。設載波頻率 f0=fs/4=50kHz，令fi=f0+δ?Δf，將 δ在區(qū)間［0，0.5］上均勻分成20個頻率點，對每個分點進行500次蒙特卡洛模擬。實正弦信號的頻率估計方差下限（即CRLB）為［12］

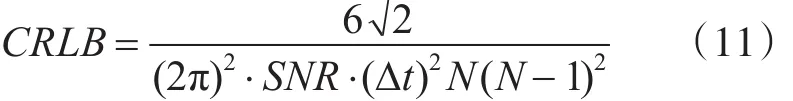
在信噪比SNR分別為2、0、-2 dB的條件下分別使用Rife算法和改進Rife算法對上述仿真信號進行頻率估計，各算法的估計均方誤差曲線如圖4所示。

從圖4可以看出：當信號的次大譜線幅度比較小，即相對頻率偏差δ比較小時，Rife算法的頻率估計誤差比較大；改進Rife算法在較寬信噪比條件下，無論相對頻率偏差δ取-0.5～0.5之間的任何值，該算法都能準確地估計信號的頻率。可見：不管在估計的精度還是穩(wěn)定性上，本文提出的改進Rife算法都明顯優(yōu)于Rife算法。

為了檢驗算法的抗噪能力，在信噪比范圍-5dB～5dB，頻率 f0=30kHz的條件下，對每個信噪比獨立試驗200次，得到2種算法的頻率估計均方誤差（Mean Square Error）曲線如圖5所示。

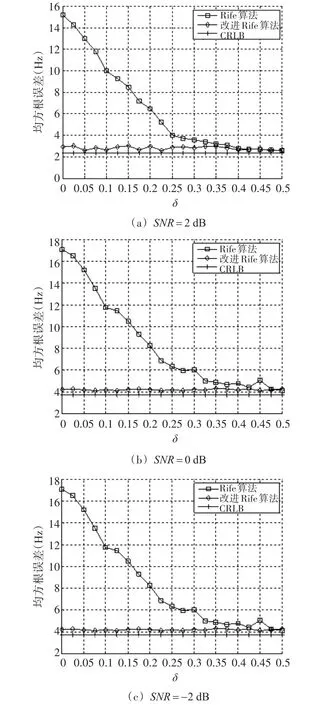
圖4 Rife算法和改進Rife算法在不同信噪比下的估計均方誤差曲線

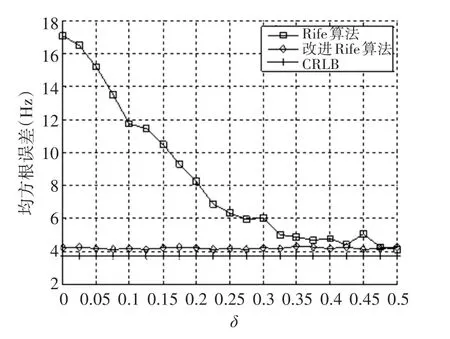
圖5 2種算法頻率估計均方誤差曲線

從圖5可以看出：Rife算法在信噪比較低時，估計性能明顯下降；而本文提出的改進Rife算法在很寬的信噪比范圍內估計誤差都比較小且與CRLB十分接近。因此，改進Rife算法的抗噪能力相比于Rife算法有了較大提高。另外本文對各個頻點的頻譜細化次數做了統(tǒng)計，并計算出其平均值i=0.4382。從計算結果來看，改進Rife算法的計算量相比于Rife算法增加的并不是很多。

6 結語

Rife算法是一種常用的基于FFT插值的頻率估計算法，具有計算速度快、實時性能好、利于硬件實現(xiàn)等特點，在工程領域得到了廣泛的應用。本文在對Rife算法進行分析基礎上提出了一種改進Rife頻率估計算法。仿真結果表明本算法準確有效，能夠效地提高Rife算法的頻率估計精度和穩(wěn)定性，估計誤差接近CRLB；且算法簡單、計算量小、能夠較好的解決傳統(tǒng)頻率估計算法在估計精度和計算量上的矛盾，具有較大的工程應用價值。

［1］萬靈達，楊曉光.一種基于FFT的高精度頻率估計算法［J］.電子科技，2010，23（10）：79-81.WAN Lingda，YANG Xiaoguang.A high-accuracy frequency estimation algorithm based on FFT［J］.Electronic Science&Technology，2010，23（10）：79-81.

［2］王宏偉，趙國慶，齊飛林.一種實時精確的正弦波頻率估計算法［J］.數據采集與處理，2009，24（2）：208-211.WANG Hongwei，ZHAO Guoqing，QI Feilin.Real-time and accurate single frequency estimation approach［J］.Journal of Data Acquisition&processing，2009，24（2）：208-211.

［3］齊國清.利用FFT相位差校正信號頻率和初相位估計的誤差分析［J］.數據采集與處理，2003，18（1）：7-11.QI Guoqing.Error analysis of frequency and phase estimations based on phase difference of segmented FFTs［J］.Journal of Data Acquisition&processing，2003，18（1）：7-11.

［4］D.Rife，R.Boorstyn.Single tone parameter estimation from discrete-time Observations［J］.IEEE Trans.on Information Theory，1974，20（5）：591-598.

［5］B.G.Quinn，P.Kootsookos.Threshold behavior of the maximum likelihood estimator of frequency［J］.IEEE Trans.on Signal Processing，1994，42（11）：3291-3294.

［6］丁康，江利旗.離散頻譜的能量重心校正法［J］.振動工程學報，2001，14（3）：354-358.DING Kang，JIANG Liqi.Energy centrobaric correction method for discrete spectrum［J］.Journal of Vibration Engineering，2001，14（3）：354-358.

［7］鄧振淼，劉渝.正弦波頻率估計的牛頓迭代方法初始值研究［J］.電子學報，2007，1（1）：104-107.DENG Zhenmiao，LIU Yu.The starting point problem of sinusoid frequency estimation based on Newton's method［J］.Acta Electronica sinica，2007，1（1）：104-107.

［8］陳奎孚，王建立，張森文.頻譜校正的復比值法［J］.振動工程學報，2008，21（3）：314-318.CHEN Kuifu，WANG Jianwen，ZHANG Senwen.Spectrum correction based on the complex ratio of discrete spectrum around the main-lobe［J］.Journal of Vibration Engineering，2008，21（3）：314-318.

［9］張強，張頻，張明童.加三角窗的頻譜校正［J］.振動與沖擊，2009，28（2）：96-98.ZHANG Qiang，ZHANG Pin，ZHANG Mingtong.Spectrum correction with a Triangular Window［J］.Journal of Vibration and Shock，2009，28（2）：96-98.

［10］胡東，李東生.三次插值頻率估計估計的改進算法［J］.計算機工程與應用，2010，46（24）：154-156.HU Dong，LI Dongsheng.Improved algorithm of cubic interpolated frequency estimation［J］.Computer Engineering and Applications，2010，46（24）：154-156.

［11］齊國清，賈欣樂.插值FFT估計正弦信號頻率的精度分析［J］.電子學報，2004，32（4）：625-629.QI Guoqing，JIA Xinle.Accuracy analysis of frequency estimation of sinusoid based on interpolated FFT［J］.Acta Electronica sinica，2004，32（4）：625-629.

［12］劉銀恩.高精度頻率估計算法研究［D］.南京：南京理工大學，2007.LIU Yinen.Research on high precision frequency estimation algorithm［D］.Nanjing：Nanjing University of Science and Technology，2007.